潮流能水轮机单桩基础的海床动力响应

2023-10-17张继生

长江科学院院报 2023年10期

张继生,赵康,陈浩

(1.河海大学海岸灾害及防护教育部重点实验室,南京 210098; 2.河海大学港口海岸与近海工程学院,南京 210098)

0 引言

面对传统能源枯竭和化石燃料引发的环境问题,自21世纪以来全球许多国家开始广泛关注和持续投入可再生能源的开发和利用,以确保可持续能源供应[1]。在中国,研究和开发可再生能源是实现“2030碳达峰、2060碳中和”战略目标的重要途径之一[2]。作为海洋可再生能源的重要形式,潮流能具有储量丰富和无污染等特点,具有广阔的发展前景[3]。全球潮流能技术发电总量可达120 GW以上,我国的潮流能总量超过8 GW[4]。与其他海洋可再生能源相比,潮流能具有较高的能量密度和强大的可预测性优势[5]。

已有的波流-海床-桩基础相互作用的研究主要聚焦桩身受力、桩周冲刷以及海床动力响应情况。Qi等[6]通过波浪水槽试验深入探究了波流与单桩及海床之间的耦合过程。结果表明,水流与波浪的叠加显著改变了桩周流场和孔隙水压力的分布。Sui等[7]利用全动力响应方程分析了单桩周围非均质土体特性对海床响应的影响,发现非均质海床的孔压值远高于均质海床。Duan等[8]采用OpenFOAM建立了波流作用下方形桩周围海床瞬态液化的数值模型。研究结果表明单桩截面形状与振荡孔隙水压力的分布直接相关,但与海床最大液化深度的联系甚微。此外,瞬态液化深度和振荡孔隙水压力受流速和渗透系数的影响显著。随后,Duan等[9]提出了新的PORO-FSSI-FOAM模型,进一步研究了波流夹角对桩周围海床的孔隙水压力和垂向有效应力的影响。研究发现,波浪和水流相互作用的随机性不仅影响孔隙水压力和垂向有效应力的空间分布,还对单桩周围海床的最大瞬态液化深度产生影响。

针对此类问题的研究,大部分关注水流、波浪作用下海床中单桩周围动力响应和土体液化问题[10],尚未考虑潮流能水轮机叶轮转动引起的波浪形态和流场的改变以及桩基础对海床土体动力响应的影响。潮流能水轮机单桩插入海床,首先单桩对流体的阻碍作用会导致桩前和桩后处流体的流速和流向等特性发生变化[11];其次单桩与海床的三维接触面会使桩周围海床由于应力集中导致的海床动力响应过程更为复杂[12];水轮机叶片的转动会对波浪形态产生干扰,使桩周的流场复杂化[13],叶片的周期性转动也会改变桩所受到的荷载,从而对单桩周围的海床动力响应造成影响[14]。因此,对波流作用下潮流能水轮机周围海床稳定性和液化深度的研究具有重要意义。

1 控制方程

1.1 波流子模型

本文基于动能定理与动量方程在波流子模型中进行研究,并通过雷诺平均的纳维-斯托克斯(RANS)方程和k-Omega SST模型控制流体,控制方程是RANS方程,即:

(1)

(2)

式中:ufi为平均流动速度矢量;pf为平均流体压力;gi为重力加速度的第i个分量;k为紊流的动能;i和j(分别可取1、2、3)为三维波流模型的3个方向;τfij为湍流应力。

k-Omega SST模型是一种混合模型,结合了k-Epsilon模型和k-Omega模型的优点。该模型在边界层区域使用k-Omega模型,而在远离边界层的自由湍流区域使用k-Epsilon模型,从而在不同流动条件下都能表现良好。其中k-Epsilon模型方程为:

(3)

(4)

式中:υ为运动黏度;υt为湍流运动黏度;ρ为密度;μ为动力黏度;μt为湍流动力黏度;σε为Epsilon的湍流普朗特数;Cε1和Cε2为常数;f1和f2为修正因子;Pk为湍流动能的产生项;Sε为源项。

k-Omega模型为

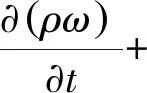
(5)

式中:ε为湍流耗散率(m2/s3);ω为比湍流耗散率(1/s)。两者均描述湍流动能的耗散强度。

OpenFOAM的数值模型中,在有重力作用以及其他源项的情况条件下,存在二相不可容体系动量方程为[15]

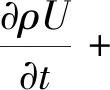
(6)

式中:p为压力;U为速度;t为时间;τ为剪切应力;g为重力加速度;F为相的表面张力。其中,

τ=v∇U。

(7)

因考虑到2种流体都具有不可压缩性,即对于某一特定流体微元,其物质导数是0,因此有连续性方程,即

∇U=0 。

(8)

此外,具有不可压缩性的流体体积法(Volume of Fluids,VOF)模型的相方程为

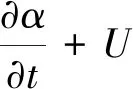
(9)

式中α在二相流中用以表示第一相中的流体体积占其网格单元体积百分比的百分数,即相体积分数。

设定其中第一相为水,第二相为大气,则当α= 1时表征网格单元内充满水,当α= 0时表征网格单元内充满空气,当0 <α< 1时则表征网格中水气混合,存在自由液面。

考虑到相体积分数及二相在交界面存在表面张力,将动量方程扩展成

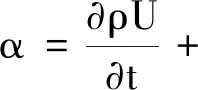
∇(v∇U)-∇Uv+gh∇ρ。

(10)

式中:h表示网格单元体心的方位;矢量σ表示表面张力系数;k表示二相在交界面处的曲率。当考虑二相流时,ρ与ν的定义为:

ρ=α1ρ1+(1-α1)ρ2;

(11)

ν=α1ν1+(1-α1)ν2。

(12)

式中:α1、ρ1、ν1分别表示第一相的体积分数、密度和运动黏度;α2、ρ2、ν2分别表示第二相的体积分数、密度和运动黏度。

1.2 海床子模型

Biot理论被广泛应用于海床动力响应研究[16]。在海床模型中,土壤骨架被视为具有弹性各向同性的物质,孔隙流体被假定为可压缩且遵循达西定律[17]。对于三维问题,控制方程可以表述为[18]:

(13)

(14)

(15)

式中:ρf为孔隙水的密度,ρ=(1-n)ρs+ρf,ρs为土壤的密度;γw表示孔隙水的重度;n表示土壤孔隙率;∈s表示体积应变;us和ws分别表示在x和z方向上的土壤位移;∇表示拉普拉斯算子;β表征孔隙流体的可压缩性,与孔隙流体的表观体积模量和饱和度有关。

1.3 边界条件

在波流子模型中,为了准确进行海岸工程的模拟数值,需要指定几个边界条件。本研究采用Airy波理论来生成入口条件的渐进波[19],并同时采用主动波浪吸收理论来防止入射波在出口处的反射。海床表面边界被定义为滑移边界条件,而上边界则使用压力出口条件来模拟大气边界。有关波浪生成和波浪吸收的详细信息可参考Higuera等[20]的研究。

在海床子模型中,本研究采用了多种边界条件来评估波浪-水流-海床-水轮机的相互作用。在海床表面,海床表面的孔隙水压力ue等于波流子模型中波浪压力Pb,同时笔者也考虑了单桩基础表面的边界条件,以确保模拟的准确性。海床表面处,由于z方向上的有效应力相对于波浪压力来说很小(<2%),可以忽略不计,即

ue=Pb,σz′=0 。

(16)

在海床底部,采用不透水刚性边界条件,其中土壤位移和垂直流动梯度被视为0,即

(17)

在侧边界方面,采用无流(零梯度)和零土壤位移边界条件,则有

(18)

波流子模型与海床子模型间的单向耦合过程如图1所示。这2个子模型均基于OpenFOAM开源代码进行离散求解。

图1 波浪-潮流-海床-水轮机相互作用的单向耦合数值模拟流程Fig.1 Outline of one-way coupling process for numerical modelling of wave-current-seabed-turbine interactions

2 模型验证

通过比较数值模拟结果与物理模型试验结果,验证了该模型在模拟潮流能水轮机对底部海床动力响应方面的有效性。在波流子模型部分,主要比较试验与数值模拟所得的流速和自由波面;在海床子模型部分,主要比较试验与数值模拟所得的孔隙水压力。

试验水槽中的布置如图2所示,试验工况参照表1。物理模型试验的潮流能水轮机采用光敏树脂材料进行3D打印制作,叶轮直径D为30 cm,单桩基础直径6 cm,质量约5 kg,埋深26 cm,试验水深为48 cm,粗砂层厚度为32 cm,其密度约为2.65×103kg/m3,水轮机轮毂深度为24 cm,叶尖速比(Tip-speed Ratio,TSR)为4。

表1 试验组次Table 1 Experimental groups

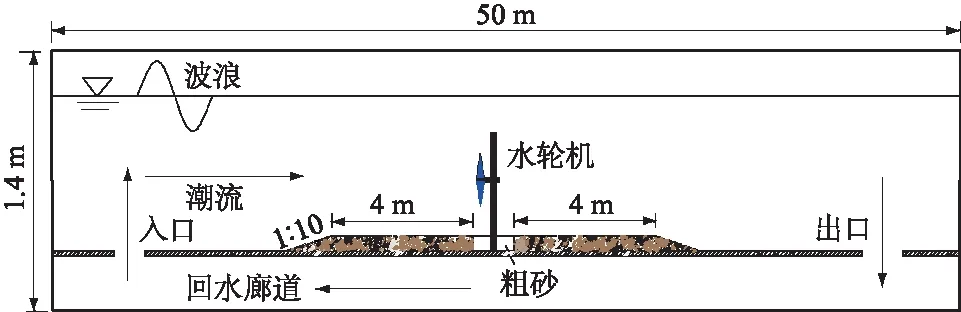
图2 波流水槽方案Fig.2 Scheme of wave-current flume

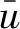
图4显示了桩前2D和桩后2D距离处测量截面的自由波面对比结果。其模拟时的水流流速、波浪参数、水深、轮毂深度等条件与工况1试验相同。观察图4可知,工况1下数值模拟结果均与试验结果吻合良好。

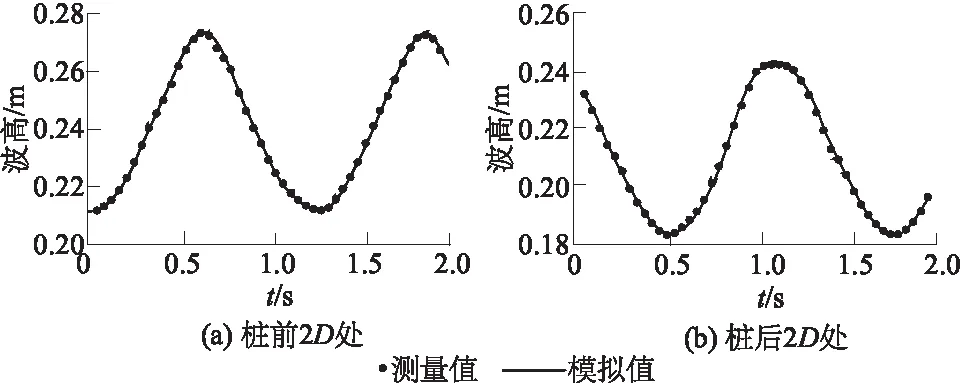
图4 自由波面数值模拟结果与试验结果对比Fig.4 Comparison of free wavefront between numerical simulation and test

在2种工况下,桩前0.06 m处的点P3个不同的深度的超静孔隙水压力变化与物理试验的对比结果如图5所示。观测点的深度分别为0.02、0.10、0.20 m。图中y轴表示为量纲一化的超静孔隙水压力,x轴为时间t(s)。通过对比图形数据,可以观察到数值模型中的超静孔隙水压力振幅与物理试验结果之间存在较好的一致性。

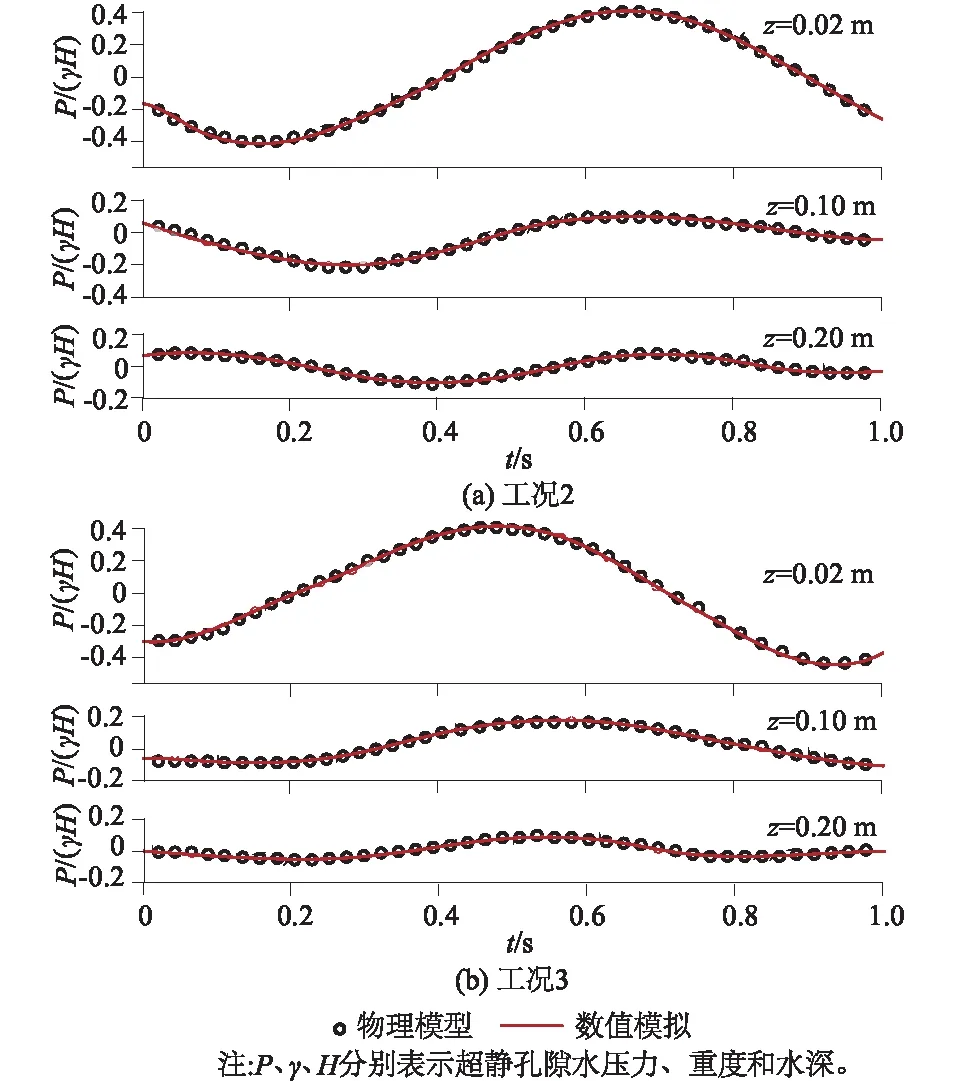
图5 工况2和工况3桩前P点超静孔隙水压力变化Fig.5 Changes in excess pore pressure at point P in front of the pile in operational condition 2 and condition 3

综上所述,数值模型的整体变化趋势与试验结果相符,表明数值模型在模拟孔隙水压力方面具有较高的可信度和准确性。

3 结果与分析

基于验证后的数值模型,本节将探讨波浪和水流作用下潮流能水轮机单桩基础周围均质海床动力的响应过程。潮流能水轮机单桩基础竖直插入海床,受波浪和水流荷载作用,其网格如图6所示。海床、单桩和流体的数值模拟工况参数见表2。

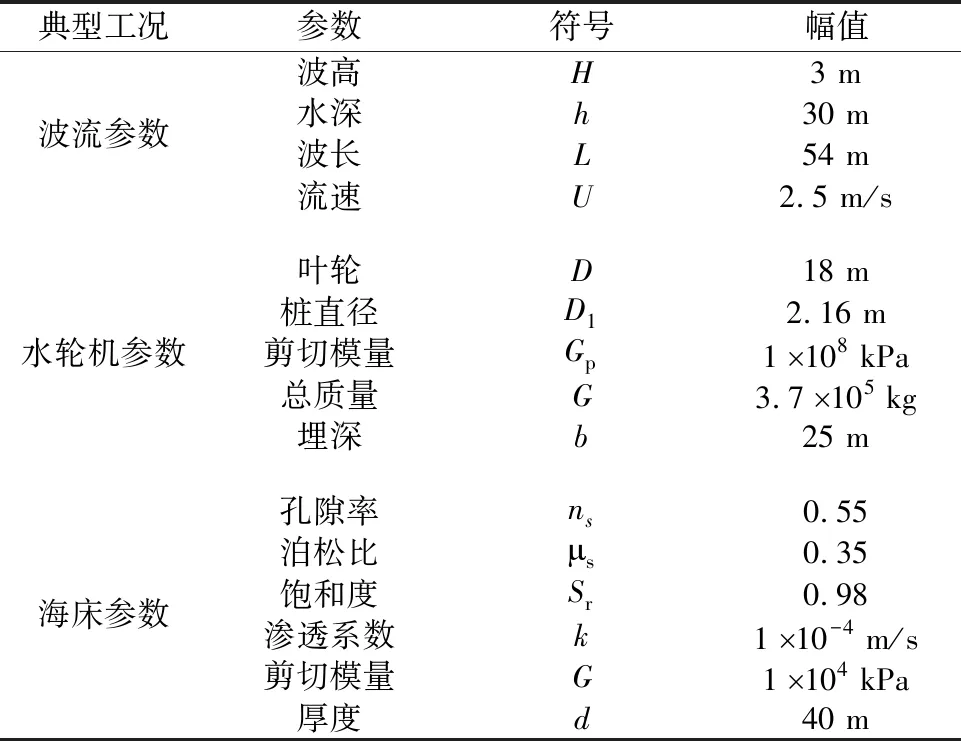
表2 数值模拟工况参数Table 2 Numerical simulation parameters

定义波浪类型为Airy波,Airy波理论是描述水波传播的一种数学模型[19]。根据该理论,波浪的传播速度取决于水深和波长,而波高则由波浪的传播速度和水深共同决定。

本研究的设计工况主要参考舟山潮流能示范工程的实测数据[21]。在本节中,选取单桩基础周围海床表面A、B2个观测点进行研究。A和B分别位于单桩基础的的迎水面和背水面,距桩柱中心2 m,见图6。在波浪传播过程中,波谷传播至结构物附近时,海床中孔隙水压力呈负值,此时海床瞬态液化深度最大[22]。因此,本节将针对波谷周围时刻作用下,研究波浪和水流荷载对单桩周围海床动力响应。

潮流能水轮机的周期性旋转对其单桩周围的海床动力响应的影响,是本文研究的核心出发点。因此,本节在T1工况的基础上进行进一步探究,将单桩基础的水轮机模型改为无转子的单桩基础模型,其他波流条件与海床特性不变,将此工况命名为T2,具体参数如表3所示。

表3 不同工况条件波流参数Table 3 Wave-current parameters in different operational conditions

本文的波流子模型和海床子模型均基于OpenFOAM环境构建。在模型集成中,研究采用了单向耦合算法,用于处理2个独立的域,并在2个子模型之间的边界处进行单向耦合。为了优化计算成本,在完成水动力过程的模拟后,笔者采用了匹配时间方案和非匹配网格系统相结合的单向耦合过程。波流-海床子模型的单向耦合过程如图1所示。具体而言,首先给定波浪和水流参数,通过blockMesh/setField程序生成并定义潮流能水轮机和单桩基础的几何形状和土壤性质等。完成预处理后,波浪模型通过RANS和VOF方程实现流体域中压力与速度的耦合。为保持计算稳定性,时间间隔设定为0.02 s。完成全时刻120 s的模拟后,从中提取50～120 s时间段的模型稳定区间的波压力数据Pb作为测量结果,并输入海床子模型。接下来,采用UP-FOAM求解器对海床模型进行时域求解,以获得波流作用下的海床和水轮机单桩的动态响应,其中包括孔隙水压力、剪切应力、有效应力等数据。

3.1 水轮机旋转对动态波压力的影响

图7为单桩基础前方海床表面A点处的动态波浪压力变化。从图7可观察到水轮机叶轮的周期性旋转显著增强了动态波浪压力。当减去30 m的静水压强后可以发现,与无转子的单桩基础相比,在水轮机叶轮周期性旋转下的动态波浪压力增强了约75%。这一结果显示潮流能水轮机叶轮的旋转明显提升了桩基附近的动态波压力。上述分析进一步强调了研究潮流能水轮机对单桩基础周围海床动力响应影响的必要性。

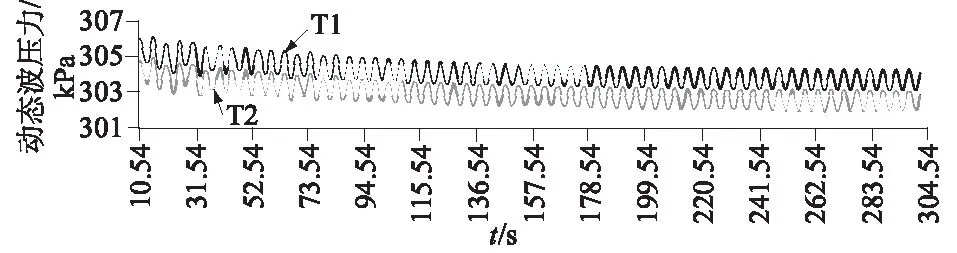
图7 桩基前方A点动态波压力对比Fig.7 Comparison of dynamic wave pressure at point A in front of pile foundation

3.2 水轮机旋转对波浪的影响

由图8可知,水轮机叶轮的周期性旋转显著增大了单桩基础后方的波高。与无转子的单桩基础相比,TSR为6时的潮流能水轮机后方B点处的波浪周期、波长、水深等特性基本没有改变,但波高增大了约15%。研究表明潮流能水轮机的转动对单桩基础周围的波高产生重要影响。

3.3 水轮机旋转对振荡孔隙水压力的影响

图9显示xz向上的波浪压力分布,其中图9(a)对应T1工况,图9(b)对应无转子的T2工况。结果表明,两者孔隙水压力在桩基附近的海床xz面上的分布基本相似,但幅值存在明显差异。值得注意,潮流能水轮机的周期性旋转增强了单桩基础后方的孔隙水压力的负压值,负压最大值增加了约24%。如3.1和3.2节所述,水轮机转子的旋转使得桩基前后的波高、动态波压力等均有显著的变化,当动态波压力传递到海床面以下时则对孔隙水压力产生了增强效应。

图9 xz向振荡孔隙水压力沿海床深度的分布Fig.9 Distribution of oscillating pore water pressure in the xz direction along the depth of seabed

3.4 水轮机旋转对剪切应力的影响

3.4.1 横剖面上剪切应力τyz

图10显示了横剖面上的的剪切应力τyz分布,其中图10(a)对应T1工况,图10(b)对应无转子的T2工况。结果表明,波谷时两者τyz在海床横剖面上的分布基本相似,但T1工况的τyz明显大于无转子的T2工况时的τyz。很显然,潮流能水轮机的周期性旋转增加了单桩基础的横向受力[23],进而增强了桩基两侧剪切应力τyz,其最大值增加了约230%。

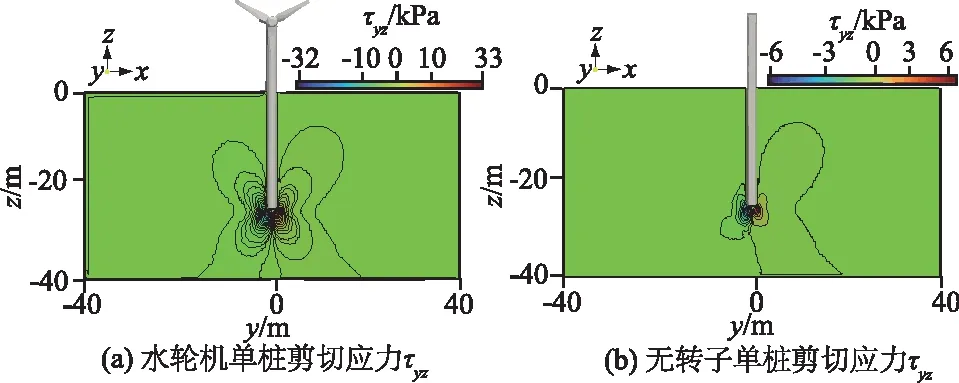
图10 横剖面上的剪切应力τyz沿海床深度的分布Fig.10 Distribution of shear stress τyz in cross-sectional profile along the depth of seabed

3.4.2 纵剖面上剪切应力τxz

图11显示了纵剖面上的的剪切应力τxz,其中图11(a)对应T1工况,图11(b)对应无转子的T2工况。结果表明,波谷时两者τxz在海床纵剖面上的分布基本相似,但T1工况的τxz幅值大于无转子的T2工况。很显然,潮流能水轮机的周期性旋转增加了桩基前后的剪切应力τxz,其最大值增加了约20%。

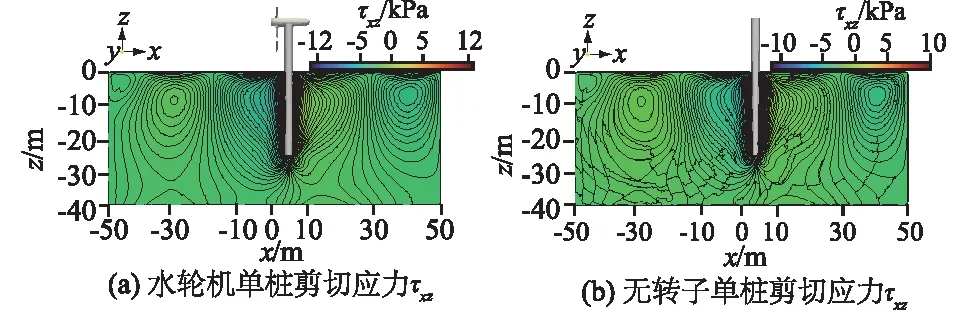
图11 纵剖面上的剪切应力τxz沿海床深度的分布Fig.11 Distribution of shear stress τxz in longitudinal profile along the depth of seabed

此外,对比图10与图11可知,无转子的单桩基础在受到波流联合作用时,其剪切应力τxz>τyz;而有水轮机周期性旋转的单桩基础在受到波流作用时,其τyz显著增大,明显>τxz。

3.5 水轮机旋转对有效应力的影响

3.5.1 点A处有效应力的垂直分布

图12显示了在测点A处海床中x、y、z这3个方向的有效应力分布。在不同工况下,x方向有效应力的变化规律基本相同:其最大值出现在海床表面,随着海床深度的增大,有效应力急剧降低至0附近。y方向有效应力的变化规律与x方向不同,在0～-4 m深度内有效应力急速减小,在-4 m处曲线出现拐点后有效应力减小的速率降低。z方向上不同工况的有效应力的变化趋势总体一致,呈先增大后减小的趋势;水轮机叶轮的旋转增大了z方向有效应力的幅值,2个工况下的最大值均出现在海床深度为-4 m左右的位置。

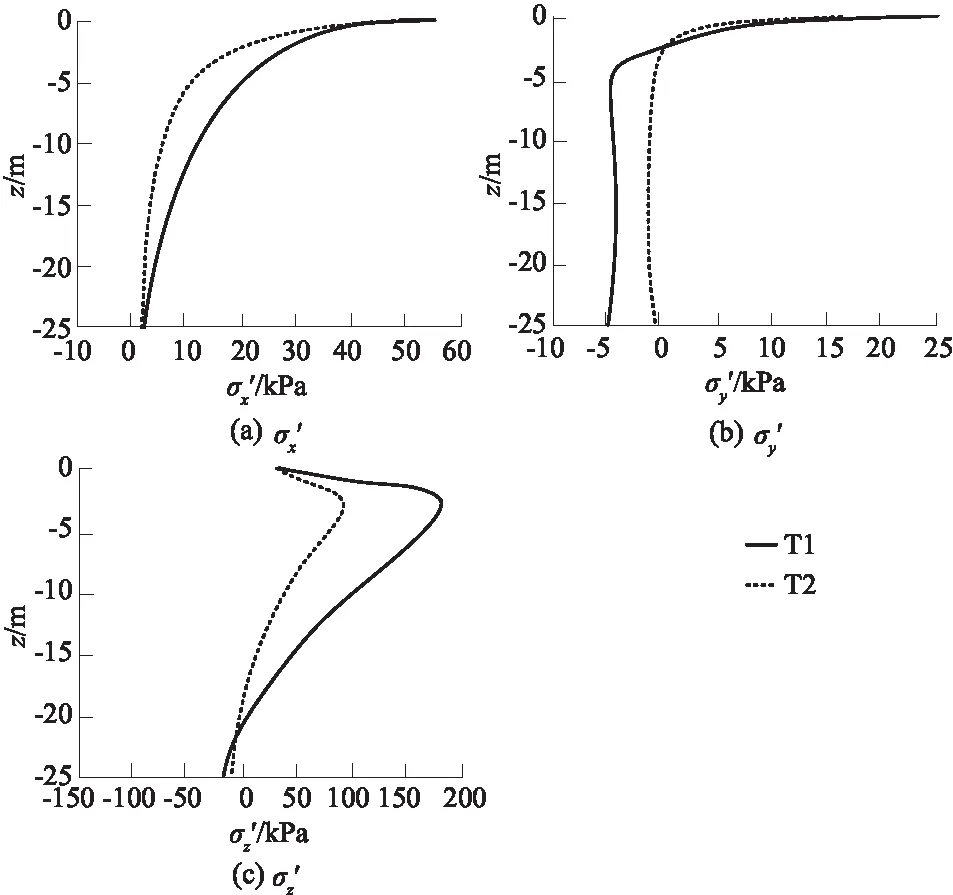
图12 水轮机桩周A点有效应力垂直分布变化Fig.12 Changes in vertical distribution of effective stress at point A around turbine pile

3.5.2 点B处有效应力的垂直分布

图13显示了B点各方向沿海床深度分布的有效应力曲线。从图13可以得出,x方向有效应力曲线先急剧减小,后缓慢增加,其主要由于受到海床内渗流力的影响[24]。同时,水轮机的转动增大了x方向有效应力值的最大值。y方向有效应力的垂向分布呈先急剧减小后缓慢增大的趋势。z方向有效应力在海床中始终为负值,且水轮机的转动增大了z方向有效应力的负压值,其中T1工况z方向有效应力曲线先急剧减小至-300 kPa左右,后缓慢增加。与桩前相比,桩后z方向有效应力的绝对值远大于前者。需要指出的是,实际工程中有效应力不可能为负,负值仅存在于数值模型计算中。

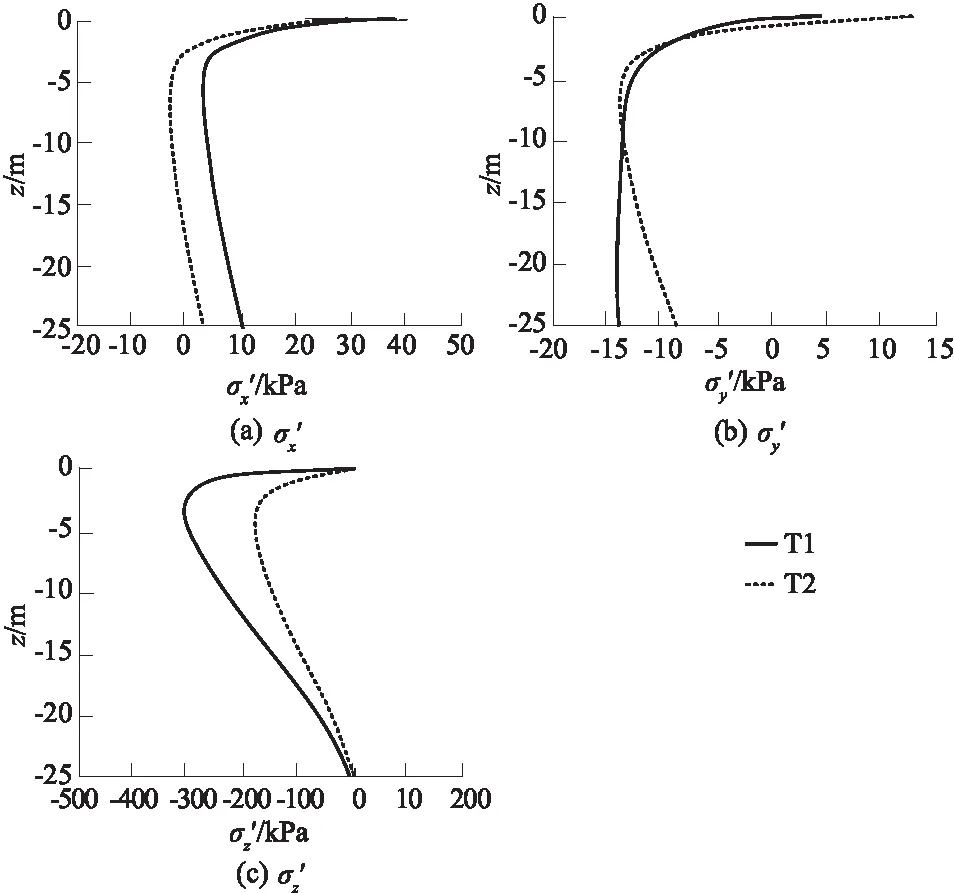
图13 水轮机桩周B点有效应力垂直分布变化Fig.13 Changes in vertical distribution of effective stress at point B around turbine pile

3.6 水轮机旋转对液化深度的影响

当土壤中颗粒间的有效应力降至0时,海床会发生液化,此时海床表层的水砂混合物呈流动状态[25]。在这种情况下,土壤无法支撑结构物的稳定性,从而导致海床失稳而对水工结构物造成损害[26]。

在三维空间中,海床瞬态液化的判断准则为[27]

(σx′+σy′+σz′)]≤0 。

(19)

式中:γs表示土体的重度;γw表示水体的重度;K0表示侧向土压力系数,不等式左侧为有效应力平均值,右侧为常量0。K0计算式为

(20)

假定压应力为正值,则由式(11)可得出,瞬态液化的判定标准可简化为

(21)

式中:σ0′表示式(19)中的第一项1/[3(γs-γw)(1+2K0)z],σ′表示式中第二项1/[3(σx′+σy′+σz′)]。

图14展示了T1、T2工况下单桩基础周围A点与B点海床瞬态液化的结果。

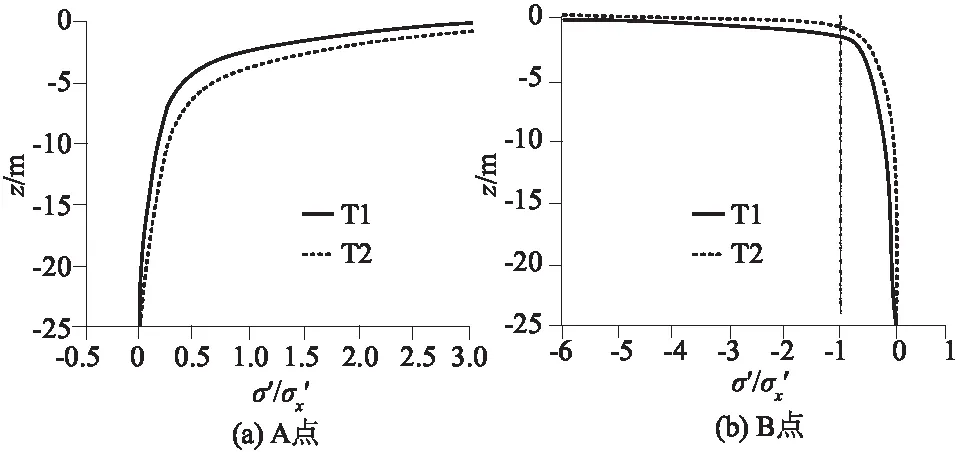
图14 液化准则判定的瞬间液化深度Fig.14 Transient liquefaction depth determined by liquefaction criteria

根据瞬态液化判断准则,桩前的海床不会发生液化,而桩后的海床会发生液化,潮流能水轮机转子的转动会增大液化深度。研究结果表明,当波流共同作用在无转子的单桩基础时,海床瞬态液化深度为1.0 m;当波流共同作用在TSR为6的潮流能水轮机单桩基础时,海床瞬态液化深度可达1.5 m。其他条件不变,水流方向与波浪流动方向相同的情况下,潮流能水轮机单桩基础下游的海床表面相较于上游容易发生液化,且潮流能水轮机的旋转将促使海床瞬态液化深度增大,液化深度的增大约50%。

在其他条件不变的情况下,潮流能水轮机叶轮的转动会导致海床土壤的液化深度增加,根据3.1和3.2节的研究可知,其主要原因如下:

(1)潮流能水轮机旋转增加了桩后方的波高。波高作为波浪三要素之一,也是表征波浪强度的重要指标[28]。波浪能量随着波高的增大而增大[29],因此桩后方波高的增大使得到达海床表面的波浪能量也随之增强,潮流能水轮机的转动增加了桩后方的液化深度。

(2)潮流能水轮机旋转增强了桩前方的动态波压力。水轮机旋转会引起动态波压力的显著提升,当提升后的动态波压力通过海床传递到土壤中,使得孔隙水压力的负压值进一步增加,土壤颗粒之间的接触力减小。当土壤颗粒之间的接触力减小到一定程度时,土壤失去了黏聚力,则更容易发生液化[30]。