常密度与变密度流体双组分溶质运移实验研究

叶 逾，刘 森，蔡芳敏，鲁春辉，谢一凡，徐 腾

(1.河海大学 水利水电学院，江苏 南京 210098；2.河海大学 水灾害防御全国重点实验室，江苏 南京 210098；3.福建省水利水电勘测设计研究院有限公司，福建 福州 350000；4.河海大学 长江保护与绿色发展研究院，江苏 南京 210098)

1 研究背景

地下水因人类活动受到严重污染，污染物中通常包含多种组分的化合物，在不同浓度条件下形成常密度或变密度对流及溶质运移过程[1-3]。例如，农田中所使用的化肥与农药，通过降雨入渗进入含水层，导致氮、磷等多种化合物在地下水中运移，形成多组分污染羽[4-5]；滨海含水层因海水入侵产生流体密度差，海水中的盐分与地下水中的其它溶质在运移过程中相互影响[6-7]。因此，正确认识常密度与变密度流体中的多组分溶质运移过程，是预测含水层中污染物运移及修复地下水的理论基础，具有重要研究意义。

常密度流体中，不同组分化合物的运移依赖于其自身的横向弥散系数[8-10]。传统的横向弥散系数参数化方程为Dt=Daqε+αv[11]，式中：Dt为横向弥散系数，m2·s-1；Daq为水动力扩散系数，m2·s-1；ε为有效孔隙度；α为弥散度，m；v为渗流速度，m·s-1。近年来，通过实验研究提出的新型横向弥散参数化方程为Dt=Daqε+Daq[Pe2/(Pe+2+4δ2)]β[12-13]，式中：Pe为Péclet数；δ为孔隙通道长度和水力半径的比值；β为量化溶质不完全混合的经验参数。传统参数化方程表明，在地下水流速较小，弥散主导溶质运移的情况下，横向弥散取决于化合物各自的水动力扩散系数；而新型参数化方程则进一步证明了，在任何地下水流速条件下，横向弥散与化合物的水动力扩散系数息息相关。变密度流体中，溶质因重力作用变得不稳定，在密度梯度的驱动下向下入渗[14-16]。有关变密度对流与溶质运移的研究，国内外学者通常聚焦于流体密度差、多孔介质非均质性、含水率、地下水流速、指流形成过程等因子的影响[17-19]，对于扩散与弥散因子的研究尚处于起步阶段[20-21]。

本文考虑化合物横向弥散效应，采用室内实验观测手段，研究变密度流体中不同化合物的运移过程，并通过与常密度流体中相应实验结果的对比，分析常密度与变密度流体中化合物之间的交互关系，揭示流体密度效应与化合物弥散效应的相互作用机理，为准确预测地下水系统中多组分污染物的运移提供理论支撑。

2 实验方法

2.1 实验装置图1所示为多孔介质流动实验装置，包括准二维砂槽、蠕动泵和连接管。

砂槽由有机玻璃制成，其内部尺寸为：长30 cm，宽1 cm，高15 cm。砂槽左右两侧均开设有15个小孔，相邻两孔之间的距离为1 cm。为保证砂槽不发生渗漏，小孔由橡胶塞堵住。橡胶塞中插入内径为0.7 mm的不锈钢针管，用于注射及抽取液体。在两侧高精度24通道蠕动泵中，分别选取7个通道，通过连接砂槽及蠕动泵，实现流动系统的定流量边界条件。泵管及其它连接管的内径为0.64 mm，均不透光。

2.2 实验过程

2.2.1 溶液配制 本实验采用两种水动力扩散系数差异较大的可溶性溶质进行研究，分别为荧光素钠和氯化钠。其中，荧光素钠的水动力扩散系数为4.80×10-10m2·s-1，氯化钠的水动力扩散系数为1.61×10-9m2·s-1。两种溶液的浓度与密度关系见图2。

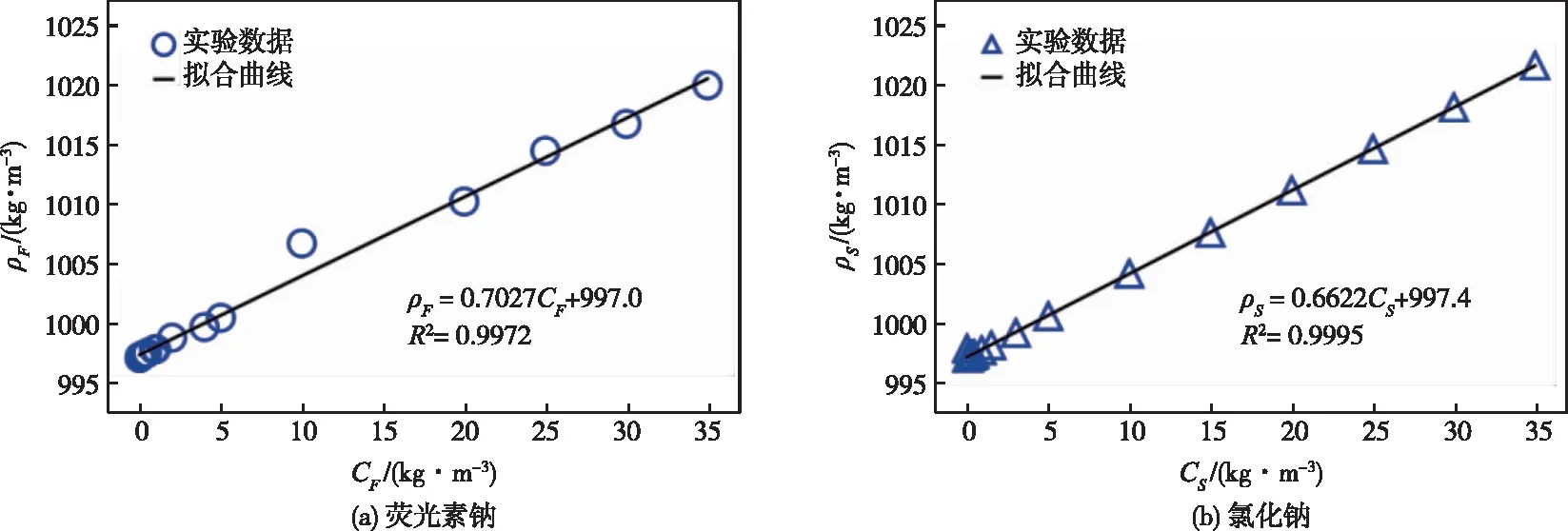
图2 荧光素钠及氯化钠的浓度-密度关系

原始溶液的浓度与密度测定方法为称重法，具体步骤为：①称量容量瓶净重；②称取溶质，置于容量瓶内；③于容量瓶中加入清水，配置成35 g·L-1的溶液；④称取容量瓶与溶液总重量，将所得结果与步骤①所得重量相减，即为溶液重量，由此可得浓度为35 g·L-1溶液的密度。利用移液器与容量瓶，同样采用称重法，将配置好的35 g·L-1溶液进行稀释，得到17种不同浓度的溶液。上述步骤②中的溶质质量可通过计算所取溶液体积与浓度(即35 g·L-1)的乘积得到。将实验所测数据进行线性拟合，可得浓度-密度线性关系，荧光素钠与氯化钠分别为ρF=0.7027CF+997.0和ρS=0.6622CS+997.4(式中：ρF和ρS分别为荧光素钠与氯化钠的密度，g·L-1；CF和CS分别为荧光素钠与氯化钠的浓度，g·L-1)，其相关系数分别为0.9972和0.9995，与实验数据吻合度高。

考虑常密度与变密度两种情况，分别将荧光素钠溶液与氯化钠溶液以体积比(Rv)1∶0、4∶1、1∶1、1∶4和0∶1进行混合，配置成5种混合溶液。5种混合溶液的密度保持一致。在常密度条件下，5种混合溶液密度均设定为997.7 g·L-1，与室温下纯水的密度(997.2 g·L-1)相似，其具体配置步骤为：①分别配置浓度为1 g·L-1的荧光素钠溶液和氯化钠溶液，并根据浓度-密度线性关系计算两种溶液的密度；②利用移液器，按照上述体积比将两种溶液进行混合；③根据密度计算公式ρmix=(VFρF+VSρS+Vwρw)/(VF+VS+Vw)(式中：ρmix为混合液密度，g·L-1；Vw为水的体积，L；ρw为水的密度，g·L-1)，计算混合液中需要加入的水量。在变密度条件下，将混合溶液的密度设置为1004.02 g·L-1，高于室温下纯水的密度，由此引发变密度流，实现与常密度实验的差异。同时，该密度条件避免了溶质羽的过快下沉，有利于变密度实验现象的观测。变密度混合溶液的配置步骤不变，仅改变步骤①中原始荧光素钠溶液和氯化钠溶液的浓度，由1 g·L-1变为10 g·L-1。

2.2.2 运移实验 准二维砂槽内部均匀填充粒径为0.4～0.6 mm的玻璃珠，填充高度为8 cm，其中，饱和区域高度为7 cm，非饱和区域高度为1 cm。表层非饱和区的作用为，防止溶液在表层自由界面形成优先通道，影响实验结果。实验采用湿填法，即在7 cm饱和区的填充过程中，保持水位自由面在玻璃珠填充面以上，由此防止饱和区中气泡的产生。

通过高精度蠕动泵控制实验渗流速度为3 m·d-1。当流动达到稳态后，将配制好的混合溶液从装置左侧的中心孔中注入，并持续观测7.2 h，间隔24 min测量出口处抽取液体的浓度。抽取样品中，氯化钠浓度的测量采用盐度计(Atago PAL-SALT)，其精度为0.1 g·L-1；荧光素钠浓度的测定采用荧光分光光度计(Perkin Elmer FL-6500)，其荧光强度的精度为0.01 mg·L-1。每个样品浓度取三次测量值的平均值。荧光素钠浓度可通过浓度-荧光强度标准曲线计算得到。标准曲线与测量值之间的拟合见图3。图中，不同浓度的荧光素钠溶液由15 mg·L-1的原始溶液稀释得到，其与荧光强度的线性关系为I=389447.91CF-689.82，相关系数为0.9994。

图3 荧光素钠的浓度-荧光强度关系

3 实验结果与讨论

3.1 溶质羽运移图4所示为稳态荧光素钠分布情况。在常密度流体中，不同体积比混合溶液的荧光素钠分布相同，均为水平对流与横向弥散的结合，两种溶质互不影响，横向弥散程度取决于各溶质的水动力扩散系数。因此，图中仅展示了体积比为1∶1混合溶液的运移情况，如图4(a)所示。

图4 不同混合比下荧光素钠溶质分布

相反，叠加密度效应后，不同体积比的混合液运移情况不尽相同。图4(b)—(f)展示了荧光素钠与氯化钠溶液在体积比分别为0∶1、1∶4、1∶1、4∶1和1∶0时荧光素钠的分布情况。当Rv为0∶1时，混合溶液为纯氯化钠溶液，因此通过肉眼无法观察运移现象。其余混合溶液的密度效应使得荧光素钠向下对流，形成不同形态的指流。尽管5种混合溶液的密度相同，然而混合溶液中荧光素钠的占比影响变密度溶质运移情况。随着Rv值的增加，荧光素钠下渗现象发生得越早，即下渗位置越靠近入口，由此可以确定，混合溶液在变密度效应下的运移受溶质间相互作用的影响。对比图4(e)和图4(f)可知，当混合溶液中荧光素钠占比较大时，混合液中荧光素钠溶质分布与单纯荧光素钠溶液分布相近，由此推断，混合液中占比较大的溶质往往主导变密度对流与溶质运移过程。另外，荧光素钠的水动力扩散系数较小，使得溶液横向弥散程度较小，密度梯度较大，由此加剧变密度对流，该物理过程可用于解释图4(e)和图4(f)中荧光素钠下渗位置更靠近入口的实验现象。图4(c)中荧光素钠的运移可能由占比较大的氯化钠溶液主导，而图4(d)中的运移则由两种溶质共同决定。

3.2 出口浓度分布图5所示为出口处测得的两种标准化溶质浓度(Cn)。标准化浓度为出口处溶质浓度与入口处对应溶质浓度的商值。

图5 出口荧光素钠与氯化钠标准化浓度分布

由图5(a)可见，在常密度流体中，混合溶液体积比对两种溶质的分布几乎没有影响。两种溶质的弥散程度完全取决于溶质的水动力扩散系数。由于荧光素钠的水动力扩散系数较小，其横向弥散程度较弱，反之亦然。

图5(b)展示了变密度流体中的出口浓度分布。变密度对流作用下，溶质与周围水体之间的接触面积增大(见图4)，导致弥散程度加强，峰值浓度降低。常密度流体中，溶质的标准化峰值浓度为0.4～0.6；而变密度流体中，溶质的峰值浓度为0.2～0.4。在变密度对流实验中，当体积比为4∶1或1∶4时，两种溶质的浓度分布保持一致，且与占比大的溶质作为纯溶液时运移情况相同。该现象区别于常密度流体中两物质的各异性运移。变密度流体中，占比大的溶质主导对流与运移过程，使得占比小的溶质跟随其进行运移，该量化分析结果与溶质分布观测结果一致。当Rv=1∶1时，荧光素钠与氯化钠的浓度分布介于两种纯溶液浓度分布之间，同样证明了变密度流体中混合物两种溶质的相互作用。

3.3 溶质稀释为了研究不同密度效应下溶质的稀释情况，采用通量相关的稀释指数进行量化。通量相关的稀释指数(EQ，m3·s-1)表示，垂直于水流方向的截面上，运移有溶质的有效体积流量，其计算公式为：

(1)

式中：N为出口有效孔的数量；qk为每个抽水孔的流速，m·s-1；Δz为两孔之间的间距，m；W为砂槽厚度，m；pQ，k的定义为：

(2)

式中Ck为每个取样孔的测量浓度，kg·m-3。

弥散作用使得溶质得到稀释，通量相关的稀释指数值越大，表明稀释程度越强。根据式(1)和式(2)可计算得到不同实验中出口处通量相关的稀释指数值，见图6。

图6 出口荧光素钠与氯化钠稀释指数

如图6(a)所示，常密度流体中，Rv值未能影响溶质的稀释程度，且荧光素钠的稀释程度低于氯化钠的稀释程度，这是由于前者的水动力扩散及弥散大于后者导致的。当叠加密度效应后，溶质的稀释程度得到显著提升(见图6(b))，并且，两种溶质在某一特定体积比时稀释程度相同，通量相关的稀释指数值与混合液中占比较大的溶质所组成的纯溶液相似，上述现象与图4及图5中的浓度分布情况相呼应，再次论证了变密度流体中混合液溶质的运移受占比较大溶质的支配这一事实。

3.4 化合物特征性为了进一步量化混合液中两种溶质运移的差别，计算了出口处两种溶质浓度的标准差(δ)，其公式为：

(3)

式中CFn，k和CSn，k分别为每个取样孔中测得的荧光素钠和氯化钠标准化浓度。不同体积比条件下的标准差结果见表1。

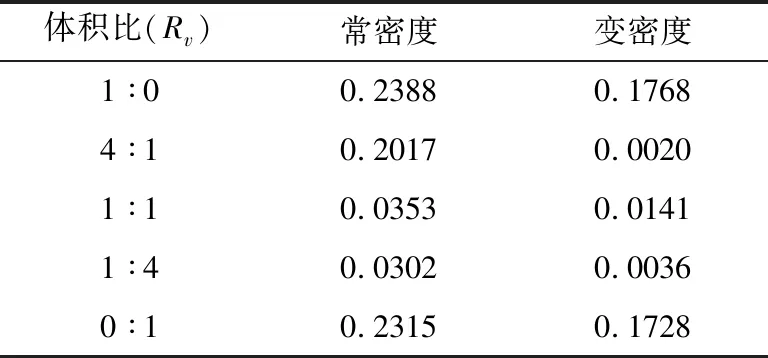
表1 出口荧光素钠与氯化钠的浓度标准差

由表1可知，任何体积比条件下，常密度流体中两种溶质的浓度标准差大于变密度流体的对应值，即混合溶液运移过程中的化合物特征性在常密度流体中更加显著，变密度效应减弱了溶质运移过程中的化合物特征性。

4 结论

利用室内准二维砂槽实验，研究了混合溶液中荧光素钠与氯化钠两种溶质在常密度与变密度流体中的溶质运移，主要结论如下：(1)常密度流体中，溶质运移的化合物特征性效应明显，溶质稀释程度取决于化合物各自的水动力扩散及弥散；(2)变密度流体中，溶质在运移过程中相互影响，占比较大的溶质主导运移，削弱了溶质运移的化合物特征性效应；(3)变密度对流过程增加溶质羽与周围水体的接触面积，使得弥散得到增强，相较于常密度流体中的溶质运移过程，溶质稀释程度得到显著提升。

以上结论有助于人们更深入地理解不同密度条件下多组分混合溶液的溶质运移情况，准确预测地下水系统中复杂多组分污染物的运移路径及浓度分布。本研究限于理想条件下的实验观察与分析，与现实场地条件存在差距。在后续研究中，应考虑更为复杂的场地条件，发展能同时考虑变密度效应与多组分混合溶液化合物特征性效应的数值模拟技术，以期进一步揭示地下水系统中多组分污染物运移的规律和内在机理。