坡度对爆炸冲击波传播影响的试验研究❋
2023-10-17姬建荣李毅卓叶希洋
陈 君 姬建荣 康 昊 李毅卓 叶希洋
西安近代化学研究所(陕西西安,710065)
0 引言
爆炸冲击波对目标的毁伤程度不仅与弹药自身的威力有关,也与爆炸时的作用环境密切相关。 对于无限空气介质,爆炸冲击波理论已有成熟的经验公式[1]。 而对于密闭或半密闭有限空间的冲击波传播理论,许多学者正在开展研究。
李秀地等[2]通过数值模拟开展长坑道中化学爆炸冲击波压力的传播规律研究。 张玉磊等[3]通过试验研究半密闭环境下方形坑道内爆炸冲击波的传播规律。 赵新颖等[4]通过仿真和试验的方法研究密闭环境下温压炸药爆炸冲击波在爆炸堡内的传播规律。 杨亚东等[5]通过建立长方体密闭结构内爆炸冲击波传播和叠加分析模型研究内爆炸冲击波的分布特性。
可以看到,学者们主要通过仿真和试验等途径进行了半密闭、密闭环境的爆炸冲击波传播规律研究。 野外实战中,场景地面多为起伏不平的山地。研究爆炸冲击波实战地形下的传播规律对野外实战防护和毁伤评估具有现实意义。 唐建曾[6]通过激波管研究了坡地对冲击波传播规律的影响。 而对于野外坡地对冲击波传播影响研究国外未见报道。
本文中,在试验场构建不同坡度的斜坡地形,在斜坡上布设超压测点,获取不同坡度的斜坡地面测点处的冲击波超压,研究斜坡地形对冲击波传播的影响,为实战防护和毁伤评估提供技术支持。
1 试验
1.1 试验布局
在试验场构建了相同宽度、不同坡度的斜坡地形。 坡度θ分别为0°(平整地面)、 ±10°、 ±20°、 ±30°。 在距坡头2.50 m 处的硬质水平地面布设梯恩梯(TNT)球形药作为爆炸源。 在距爆炸源行程距离L为2.05、2.35、2.65、2.95、3.25、3.75、4.25、4.75、5.25、5.75、6.75 m 处布设11 个超压测点,获取斜坡各处的冲击波超压p。
试验布局如图1 所示。

图1 试验布局示意图Fig.1 Test layout
1.2 爆炸源
爆炸源为TNT 压制而成的球形裸药。 在球形爆炸源中心开孔,采用15 g 的JH14(炸药型号)作为传爆药,用微型导爆索起爆球形TNT。 球形爆炸源的密度为(1.58 ±0.02) g/cm3,药量为(5.00 ±0.08) kg。 为了避免爆炸过程中地面炸坑能量消耗对试验结果的影响,试验前将球形TNT 爆炸源放置在与地面平齐的Q235 钢板(20 mm 厚)上起爆。
爆炸源结构及布设如图2 所示。
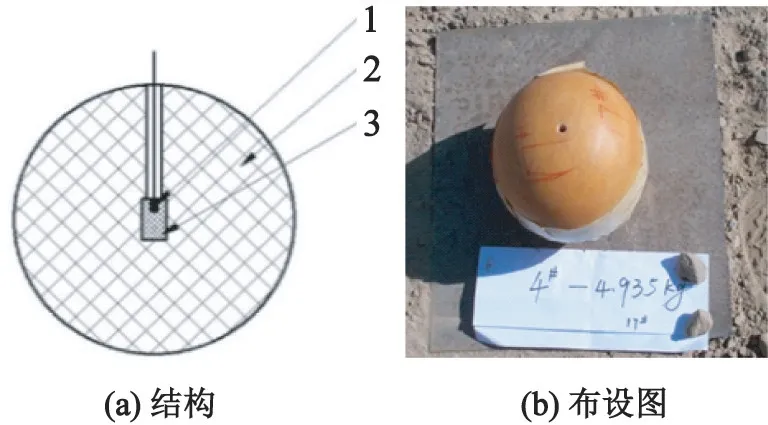
图2 爆炸源结构及布设图Fig.2 Structure and layout of the explosion source
1.3 超压测试系统
超压测试系统由壁面冲击波超压传感器、低噪声信号线、ICP 信号调理器、数据采集器等组成。 壁面冲击波超压传感器的感应面与斜坡面平齐,即与水平面的角度与坡度相同。 传感器型号为113B26,美国PCB 公司,量程3.5 MPa。 数据采样频率设置为1 MHz,系统带宽大于100 kHz。
2 结果与分析
2.1 坡度对超压峰值的影响
同工况进行了多发试验,对试验数据求平均值。图3 为坡头前2 个、坡头后3 个测点处的超压峰值对比曲线。
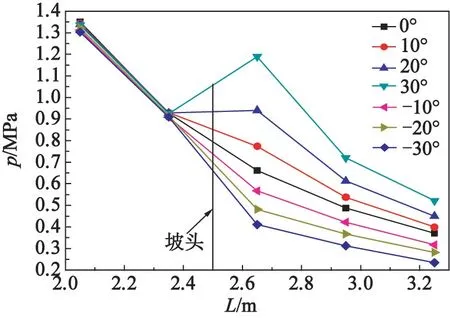
图3 不同测点处的超压峰值对比Fig.3 Comparison of the peak overpressure at different measuring points
由图3 可以看出:在坡头之前,不同工况时,2个测点的超压峰值相差不大;在坡头之后,上坡超压峰值相比平地时明显增大,且随坡度的增大而增大;下坡超压峰值相比平地时明显减小,且随坡度绝对值的增大而减小。 随着坡度的变化,超压峰值在坡头区域发生明显变化。
图4 为斜坡上各测点处的超压峰值对比。
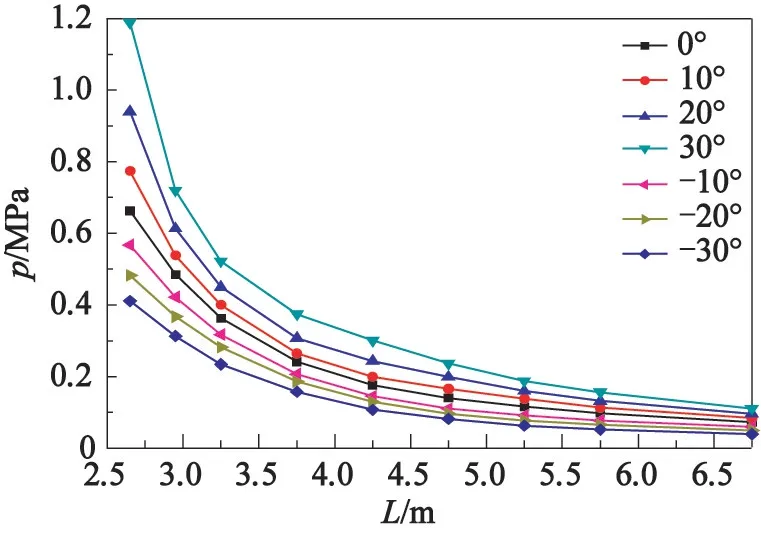
图4 斜坡上各测点的超压峰值随行程的变化Fig.4 Variation of peak overpressure at different measuring points on the slope with distance
由图4 可以看出:在上坡(θ=10°、20°、30°)情况下,斜坡上测点的超压峰值都会增大,且峰值会随着坡度的增加而增加,随着行程的增大而减小;相反,在下坡(θ=-10°、-20°、-30°)情况下,超压峰值会随着下坡角度绝对值的增加而减小,随着行程的增大而减小。 这一结论与文献[6]的结果一致。文献[6]中,利用激波管在不同的迎坡角下获取的大量数据表明了激波沿地形变化的一般规律:冲击波遇到迎坡时,坡面超压增大;遇到负坡时,超压峰值减小。 杜红棉等[7]提出,当空气中传播的冲击波遇到刚性壁面时,质点速度骤然变为零,壁面处质点不断聚集,使压力增加。 赵新颖等[4]认为,冲击波在有限空间遇到固体壁面会形成反射,在特定位置会出现聚焦现象,使冲击波超压峰值增加。 与本文的结论一致。 综上,同类型、同质量的炸药触地爆炸,由于坡度地形的影响,压力峰值与坡度有关。
为了研究斜坡地形时冲击波超压峰值增大或减小的程度,将斜坡测点的超压峰值与相同行程处测点的平地超压峰值作比值,获得超压峰值比。 超压峰值比随行程的变化曲线,如图5 所示。

图5 超压峰值比随行程的变化Fig.5 Variation of peak overpressure ratio with distance
由图5 可以看出:上坡时,超压峰值比(超压增大程度)随上坡坡度的增大而增大,也就是上坡坡度越大,超压峰值增大程度越大。 上坡时,超压峰值比呈现为振荡变化趋势:先增大,后减小,再增大,最后趋于平稳。 下坡时,超压峰值比随下坡坡度绝对值的增大而减小。 下坡时,超压峰值比同样表现为振荡变化趋势:先减小,再增大,再减小,最后趋于平稳。 这可能是冲击波遇到斜坡后空气域突变或放射等因素所致。
文献[6]中,通过激波管试验数据获得了斜坡处超压峰值的经验公式。
上坡经验公式:
式中:△pθ为斜坡处超压峰值;η+为增压系数(超压比);△p为入射压,0.01 MPa≤△p≤0.60 MPa。θ为坡度;A、B分别为系数。
下坡经验公式:
式中:η_为减压系数。
由式(1)~式(4)可以看出,增压系数(超压比)是随坡度变化的二次函数。 式(5)~式(6)表明,减压系数在0°≤θ≤20°时只与坡度相关,且是随坡度变换的指数衰减函数;在20° <θ≤90°时,是只与坡度相关的二次函数。
文献[6]中的经验公式与图5 中的曲线变化趋势有差异。 用20°上坡试验数据验证发现,式(1)~式(4)获得的增压系数整体偏大,偏差范围16%~80%。 用-20°下坡试验数据验证发现,式(5)~式(6)获得的减压系数多数偏小,偏差在-25%~7%之间。 -30°下坡试验数据验证结果同样偏小,偏差在-22%~-8%之间。 这可能与试验条件相关。
爆炸冲击波传播的研究更多关注的是对比距离、坡度和斜坡超压之间的关系。 根据试验数据,拟合了对比距离、坡度θ与增(减)压系数η的关系,三维结果如图6 所示。

图6 增(减)压系数与对比距离和坡度的关系Fig.6 Relationship between η andor θ
式中:η(,θ)为增(减)压系数;为对比距离;θ为斜坡坡度。
式(7)为增(减)压系数与对比距离和坡度的关系,拟合结果与试验结果偏差-6.08%~7.29%。
2.2 坡度对超压峰值到达时间的影响
图7 为坡头前2 个测点、坡头后1 个测点处超压峰值到达时间的对比曲线。 由图7 可以看出:冲击波遇到斜坡前,超压峰值到达时间与通过平地时相比变化不大;上坡后,超压峰值到达时间减小;下坡后,超压峰值到达时间增大。
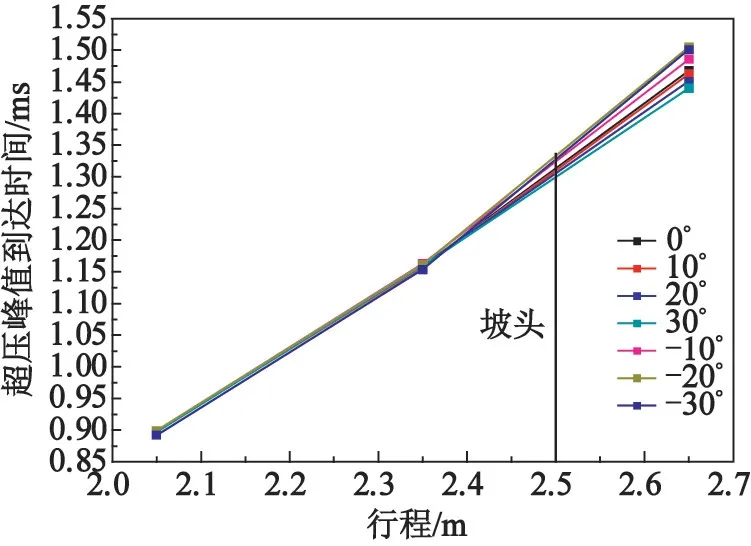
图7 不同测点处超压峰值到达时间的对比Fig.7 Comparison of the arrival time of peak overpressure at different measuring points
图8 为斜坡上各测点超压峰值到达时间的对比。 由图8 可以看出:上坡时,超压峰值到达时间随坡度的增大而减小,随着行程的增大而增大,行程越大,区分越明显;下坡时,超压峰值达到时间随着坡度绝对值的增大而增大,随着行程的增大而增大,行程越大,区分越明显。 通过试验数据,对不同坡度时超压峰值到达的时间比的均值进行拟合,得到了αθ与θ的近似关系:
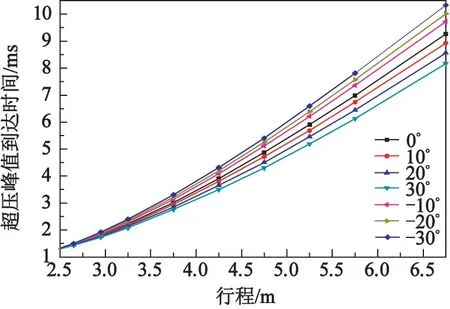
图8 斜坡上各测点超压峰值到达时间的对比Fig.8 Comparison of the arrival time of peak overpressure at different measuring points on the slope
式中:tθ为坡度为θ时超压峰值的到达时间;t0为坡度为0°时超压峰值的到达时间;αθ为超压峰值到达的时间比;θ为斜坡坡度。
2.3 坡度对超压脉宽的影响
图9 为平地和20°、-20°斜坡相应行程测点处的超压脉宽的对比。 从图9 中可以看出,相比平地,上坡时超压脉宽变小,下坡时超压脉宽增大。 脉宽的变化整体表现为振荡趋势。

图9 不同坡度时各测点处的脉宽Fig.9 Pulse width at different measuring points at different slopes
2.4 坡度对超压冲量的影响
图10 给出了平整地形和20°、-20°坡度斜坡时相应测点处冲量大小的比较。 从图10 中可以看出,坡头前、后上坡时冲量增大,下坡时冲量减小。 冲击波过坡头后,冲量同样表现为上坡增大、下坡减小的趋势,冲量变化呈振荡趋势。

图10 不同坡度时各测点处的冲量Fig.10 Impulse at different measuring points at different slopes
3 结论
1)在坡头之前的斜坡平整段处,冲击波超压峰值、超压峰值到达时间与平地时的数据相当。
2)从坡头前测点开始,上坡超压冲量增大,且随坡度增大而增大;下坡超压冲量减小,且随坡度绝对值的增大而减小。
3)上坡时,超压峰值和冲量比平地时的数据增大,超压峰值和冲量随坡度的增大而增大,超压峰值和冲量的增大程度呈现振荡变化趋势;下坡时,超压峰值和冲量比平地时的数据减小,超压峰值和冲量随下坡坡度绝对值的增大而减小,超压峰值和冲量的减小程度呈现振荡变化趋势。
4)上坡时,超压峰值到达时间比平地时的数据减小,超压峰值到达时间随上坡坡度增大而减小;下坡时,峰值到达时间比平地时的数据增大,超压峰值到达时间随下坡坡度绝对值的增大而增大。
5)超压脉宽上坡时减小,下坡时增大。
6)得出不同坡度地形时冲击波超压峰值、超压峰值到达时间与平整地面时相应值的关系式;在本文给出的条件范围内,可用于工程实际计算。
