基于蒙特卡洛法的计价器检定不确定度评定

臧晓伟 陈康 / 上海市计量测试技术研究院

0 引言

在出租汽车计价器计量工作中，计价器计程误差检定标准装置作为社会公用计量标准，开展检定或校准工作[1]需要评定其不确定度。目前，多数文献[2-5]采用GUM 方法[6]评定出租汽车计价器计程误差检定结果的不确定度。GUM 方法是计量标准装置评定不确定度所采用的最常用和最基本的方法，然而，当测量模型复杂、输入量和输出量概率密度函数（probability density function，简称PDF）非对称时，MCM 方法的应用受到一定的限制。此时，蒙特卡洛法（Monte Carlo 方法，简称MCM 法）[7]作为一种有效的评定方法，近年来，越来越多的文献[8-11]和相关标准规范[6-7]都建议用MCM 法的评定结果验证GUM 法评定结果的准确性，因此，在推动出租汽车计量工作高质量发展过程中，开展MCM 法评定测量不确定度的研究有十分重要的意义。两种方法结果的相互印证有利于加强计价器检定标准装置的准确性和科学性。

1 MCM法在计价器计程误差检定中的应用

MCM 法是通过数值模拟计算实现概率分布传播的方法，与GUM 法评定步骤相比较，两者在确定输入量和测量模型的步骤可相互参照。此外，GUM 法的标准不确定度分量的A 类评定和B 类评定的数据以及概率分布假设可为MCM 法各个输入量的PDF设定提供参考。GUM 法利用不确定度传播律计算合成标准不确定度前，需要确定各输入量的相关性和灵敏系数。而MCM 法利用数值模拟计算程序抽取大量样本值后得到输出量数据集合以及相应的标准不确定度。当MCM 法采用的样本量足够大，其模拟计算结果趋于稳定后可验证GUM 法的合理性和适用性。

在出租汽车计价器计量工作中，装车后的出租汽车计价器需要按照规程[12]规定进行首次检定和周期检定，其中计价器计程误差测量结果是判断计价器是否合格的重要依据之一。采用MCM 法评定装车后的计价器计程误差测量结果的不确定度，有助于检定人员加深理解其不确定度评定过程，并可与GUM 法评定过程相互比较（表1）。

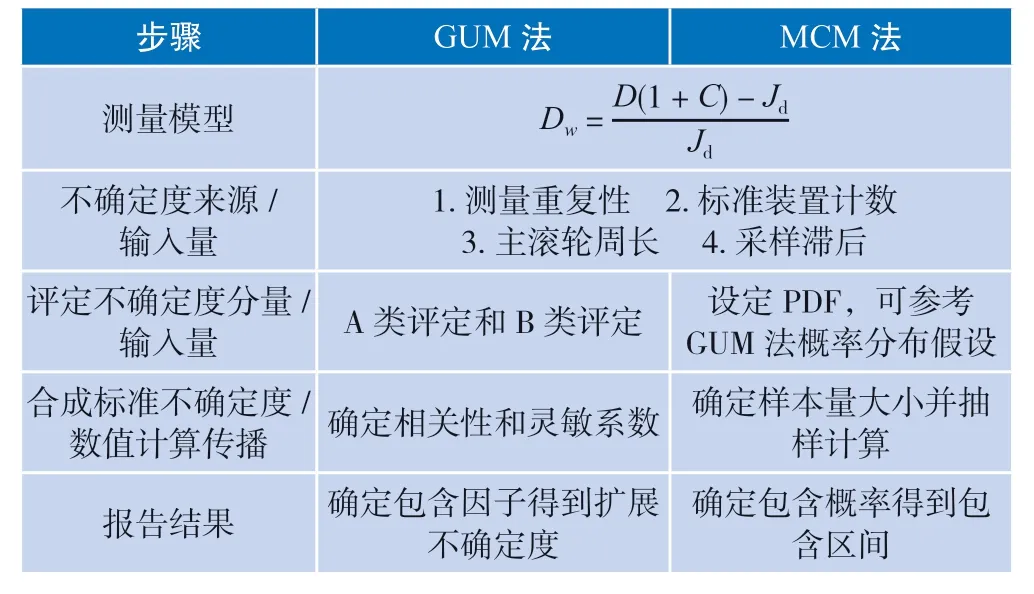
表1 比较GUM 法和MCM 法评定装车后的计价器计程误差测量不确定度的过程

其中Dw为计程误差（%），D为计价器示值（m），C为轮胎修正值（%），Jd为检定装置测量的计程值（m），其值为标准装置计数值与主滚轮周长之积。

MCM 法评定不确定度时最重要的步骤之一为设定输入量PDF，利用GUM 法评定计价器检定标准装置不确定度分量的经验、试验数据等科学依据，PDF可设定为矩形分布与正态分布。GUM 法和MCM 法在计价器检定评定不确定度应用中，都将标准装置计数、主滚轮周长与采样滞后等不确定度来源所代表的输入量的PDF 设定为矩形分布，测量重复性的PDF 设定为正态分布（表2）。

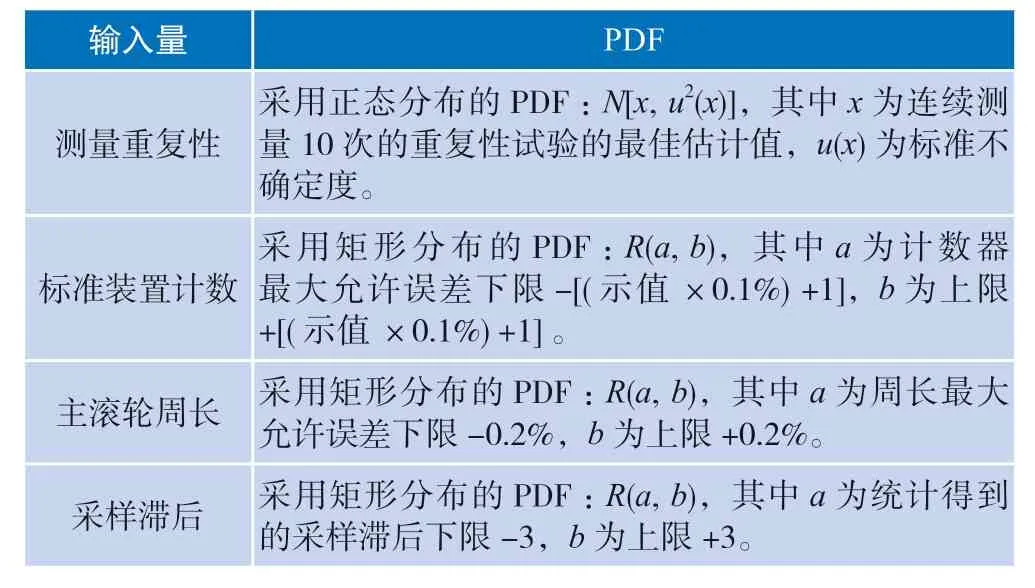
表2 MCM 法输入量设定的PDF

2 MCM法的软件实现

MCM 法需要配合数值计算编程语言或者软件实现抽样计算以及分析结果。许多学者[13]设计了具有普遍适用性的MCM 法评定测量不确定度的软件，主要基于LabVIEW、Matlab、Microsoft Excel 等商用付费软件。Python 作为一种开源跨平台的编程语言，在统计分析、科学计算、数值模拟、图形界面和数据可视化展示等方面具有成熟开源的代码库，可自由阅读并改动其源代码。利用Python 实现MCM 法评定计价器检定测量不确定度的软件开发，具备图形化界面，方便输入参数以及查看结果，其跨平台特性可在各类操作系统（Linux、Windows）以及云计算平台上运行或部署（图1）。

图1 MCM 法评定计价器检定测量不确定度程序模块设计

为方便用户操作和查看MCM 法评定计价器测量不确定度的整体过程，可以利用Python 图形界面交互库设计友好、简洁的软件界面。用户导入测量重复性数据文件，确定PDF 各项参数以及样本值后，内置算法自动执行数值计算以及数据统计，生成直方图以及报告结果区间（图2）。

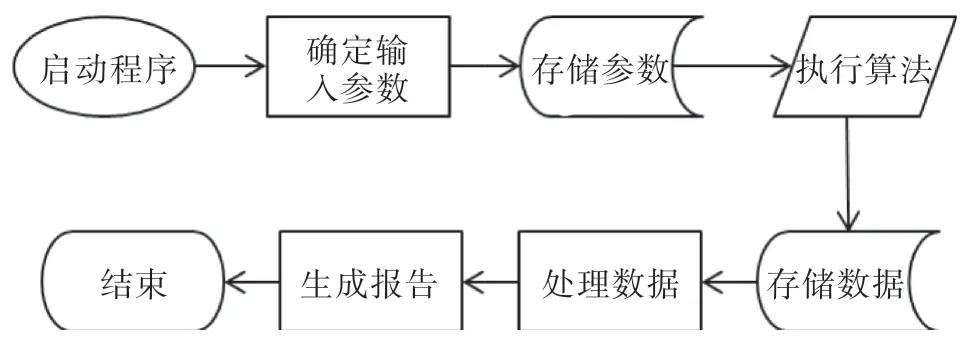
图2 MCM 法评定计价器检定测量不确定度程序执行框图

基于Python 开发的MCM 法评定计价器检定测量不确定度软件（图3）以JJF 1059.2—2012 中要求的蒙特卡洛法实施步骤为基础，专门针对计价器检定不确定度评定需求进行了优化，该软件提供直观、详细的操作和显示信息，并生成可视化的报告结果（图4）。

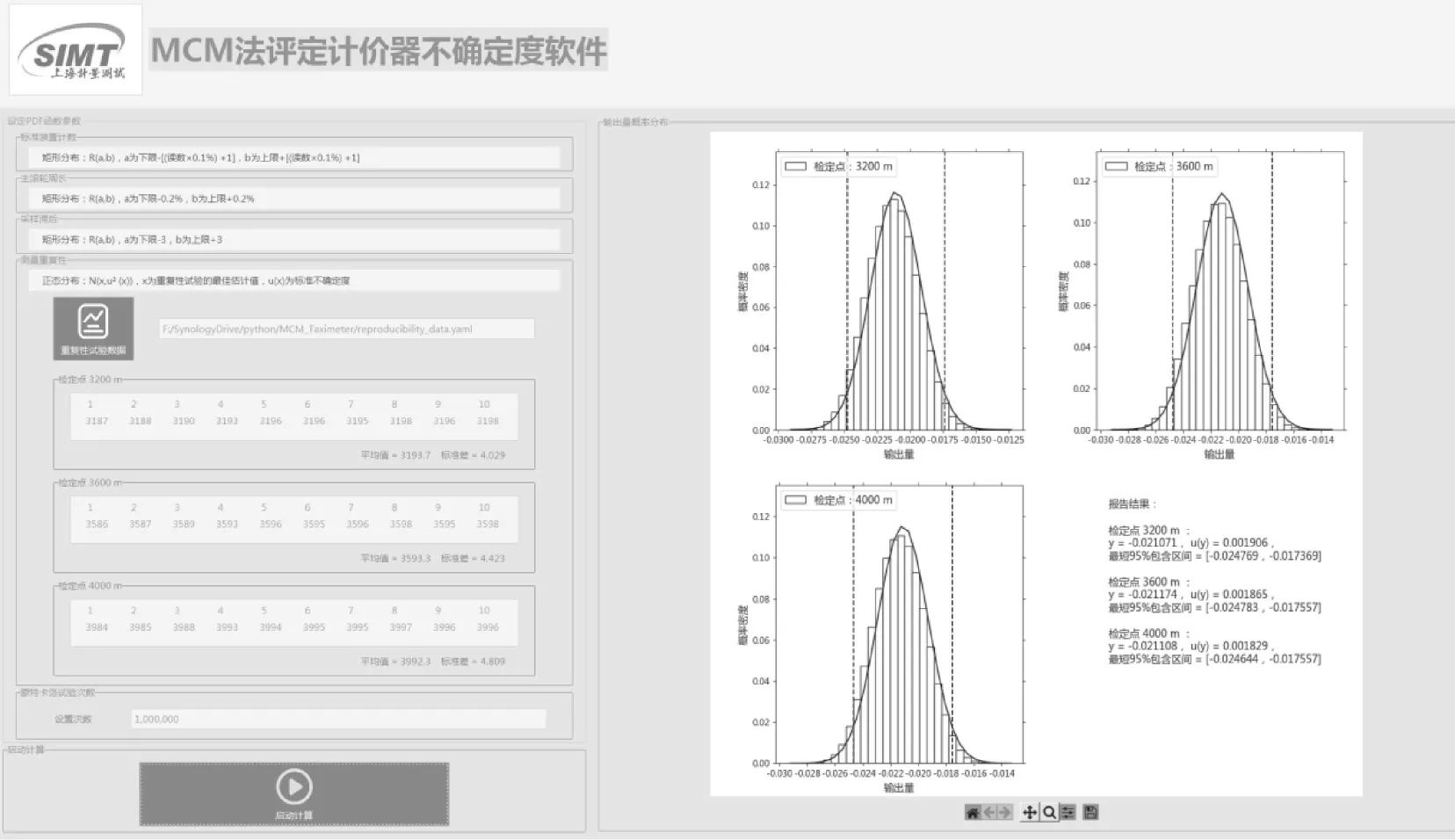
图3 基于Python 开发的MCM 法评定计价器检定测量不确定度软件截图

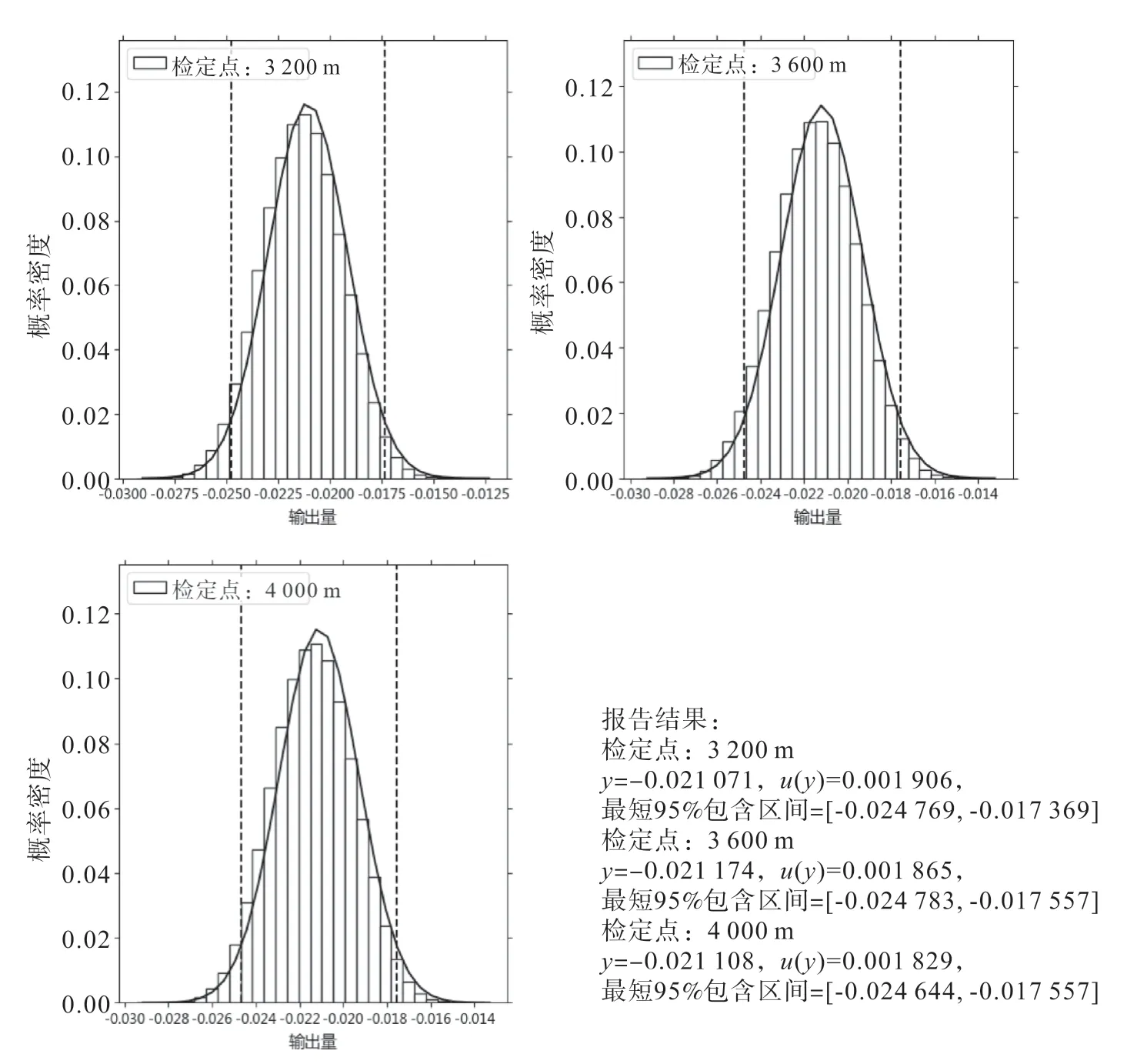
图4 软件提供的报告结果

在软件中，用户可以方便地导入计价器重复性数据文件并设置PDF 各项参数和样本值。内置算法将自动进行数值计算和统计分析，并生成直方图和报告结果区间。此外，软件还提供了多种可选项，如样本数量、抽样次数等参数设置，以满足不同用户的需求。

通过使用该软件，用户可以更加轻松地完成MCM 法评定计价器不确定度的任务，并且能够获得更加准确、可靠的测量结果。同时，直观详细的报告结果也使得用户能够更好地理解和解释评定结果，并进行更深入的分析和研究。

3 验证GUM法的结果

为了验证GUM 法的结果，按照JJF 1059.2—2012 中要求确定u(y)的数值容差δ，将u(y)表示为c×10l。取一位有效数字时，δ= 0.000 5；取两位有效数字时，δ= 0.000 05。通过以下公式比较GUM 法和MCM 法获得的包含区间各自端点的绝对偏差，当绝对偏差不大于δ时，则说明GUM 法通过验证。

式中：y—— 输出量的估计值；

Up—— GUM 法提供的扩展不确定度；

ylow—— MCM 法提供的包含区间下限端点；

yhigh—— MCM 法提供的包含区间上限端点；

dlow—— 包含区间下限端点的绝对值偏差；

dhigh—— 包含区间上限端点的绝对值偏差

根据JJF 1059.2—2012 中蒙特卡洛试验次数M=106 可以为输出量提供95%包含区间，该区间长度被修约为1 位或2 位有效数字。按照规范要求，在软件中设置相关参数后计算得到MCM 法的包含区间，并与GUM 法得到的结果进行比较。从表3 中可以看出，两者在约定的数值容差下一致，绝对偏差不大于取一位及两位有效数字情况下的数值容差。这表明GUM 法适用于计价器检定测量不确定度评定及类似的情形。

4 结语

本文采用蒙特卡洛法评定计价器检定测量不确定度，探究GUM 法与MCM 法评定过程中的差异，提出针对计价器检定专业方面MCM 法需设定的输入量概率密度函数。基于该专业的需求使用Python 研发MCM 法评定计价器不确定度软件，提供直观详细的输出量概率密度分布图以及报告结果，并验证了GUM 法的结果。结果表明，GUM 法与MCM 法都适用于计价器检定测量不确定度评定，提升了计价器检定标准装置的准确性和科学性，为今后MCM 法应用于类似标准装置不确定度评定提供指导意义。