螺杆钻具瓣齿式万向轴密封结构流固耦合分析*

张锐尧 叶道辉 肖 平 关勤勤 朱忠喜 张小俊

(1.长江大学石油工程学院 2.中石化石油机械股份有限公司)

0 引 言

近年来，随着我国油气资源勘探开发力度日益增大，仅仅对浅部地层油气资源的开采已经不能满足现有需求。未来我国油气勘探开发的重点目标是各类“难动用”的油气资源，尤其是大量深井、超深井、大位移井等复杂结构井[1-3]。由于地质条件复杂，钻井提速难题异常凸显，所以亟需开展相关提速工具研究[4-5]。螺杆钻具作为常用的钻井提速工具，可以将钻井液的液力能作为动力源，进一步将扭矩和转速传递给钻头，从而实现高效钻井[6-7]。然而，螺杆钻具的关键传动结构——万向轴的使用寿命对工具整体的使用寿命以及钻井风险具有决定性影响。现有挠性万向轴由于长度大，不利于定向钻井作业，所以不适用水平井和大位移井[5]；花瓣式万向轴在传递运动过程中，瓣齿之间会产生滑动摩擦，运动副的磨损也比较严重；球形万向轴需要对运动副外表面做特殊强化处理以增强耐磨性，并且对密封性能的要求较高[8-13]；现有密封瓣齿式万向轴的瓣齿外轮廓曲线与上、下接头内腔中内凹曲面的外轮廓曲线形成共轭曲线，其传递扭矩和转速的稳定性更好。在保证密封性能良好的前提下，该运动副的耐磨性能较好，万向轴的使用寿命也可以得到延长。但是，在钻井过程中，螺杆钻具马达转子产生的轴向拉力以及密封套内腔中液压力的综合作用，使得密封套经常发生破损或鼓胀变形，从而引起密封失效，导致运动副出现不同程度的磨损，缩短了万向轴的使用寿命，对钻井效率产生不利影响。为了探究橡胶密封套出现破损和鼓胀变形的失效机理，笔者针对密封结构开展了流固耦合分析，研究了内部流场的流动规律、最大应力和最大位移分布规律，并通过现场试验进行了验证，以期为密封结构的优化设计提供参考。

1 总体结构和原理

密封瓣齿式万向轴主要由上接头、下接头、中间轴以及三者之间的运动副密封结构组成，三维模型如图1所示。其中，中间轴两端的瓣齿外轮廓曲线与上、下接头内腔中的内凹曲面的外轮廓曲线之间形成共轭曲线，可以实现稳定啮合以传递动力。在钻井过程中，螺杆钻具的马达转子做偏心旋转运动，其与上接头通过螺纹连接，将转速和扭矩通过瓣齿啮合传递给中间轴。中间轴通过球面与球窝配合结构在一定角度内自由摆动定位，进一步地通过啮合结构将动力传递给下接头，并将转子的偏心旋转运动转换为传动轴的定轴旋转。

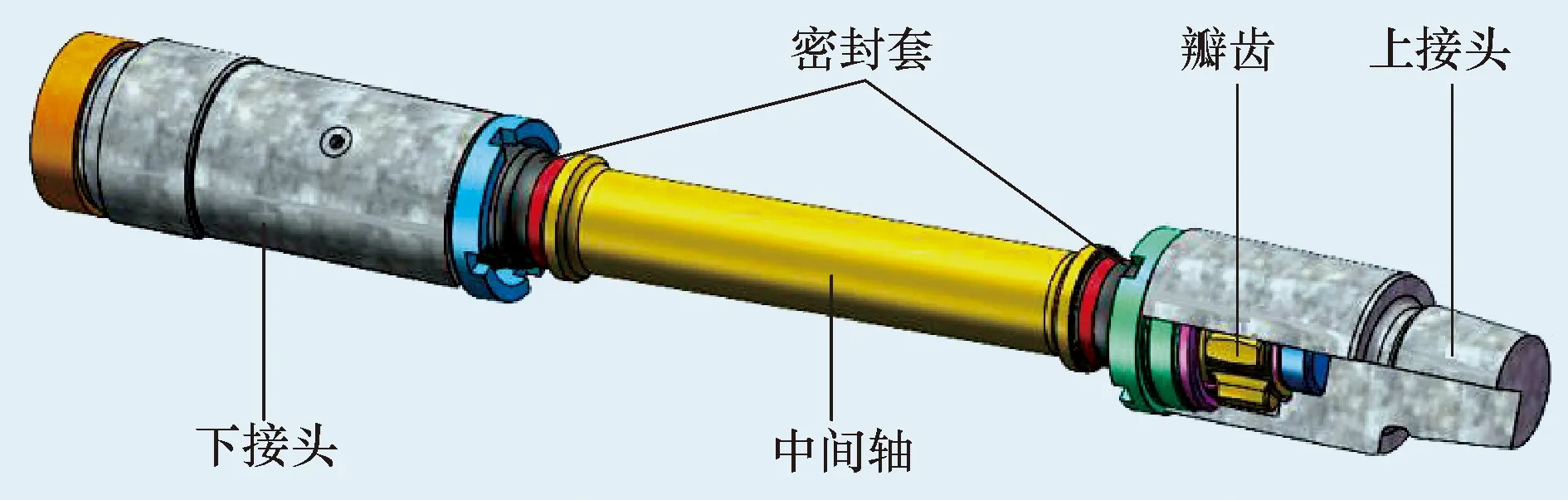
图1 密封瓣齿式万向轴三维模型Fig.1 3D model of sealed flap toothed universal shaft

综上所述，在瓣齿式万向轴传递动力过程中，马达转子在轴向上会产生一定的位移，尤其是沿着上接头右侧端面外法线方向上会产生一定的拉力。橡胶密封套一端固定在中间轴上，另一端与上接头连接，其内腔充满润滑脂。因此，密封套在轴向上为一端固定，一端承受拉力，在径向上承受内部流体的分布压力，从而引起橡胶密封套的破损或鼓胀变形。

2 仿真模型建立及结果分析

针对瓣齿式万向轴的密封结构开展了流固耦合仿真分析：一方面基于动网格方法，研究内部流场的速度与动压分布；另一方面，研究不同动压以及轴向力条件下，密封套产生最大应力和最大变形量的分布区域；最后，通过现场试验对仿真结果进行了验证。

2.1 物理模型

在密封结构内腔中充满润滑脂对运动副进行润滑。润滑脂是胶体分散体系，具有黏弹性。当不受外力作用或外力较小时，润滑脂只产生弹性变形而不流动[14-19]。在实际钻井时，受到井下高温条件以及瓣齿高速旋转所产生的较大剪切力的综合影响，润滑脂的皂纤维结构明显变稀，基础油从皂纤维结构中分离出来，进而润滑脂的黏度下降、流动性增强[20]。因此，本文将内腔中的润滑脂视为流动状态，进一步开展内部流场研究。

图2为密封结构内腔流体域和橡胶密封套网格划分结果。由于瓣齿高速旋转会在密封腔内形成旋转流场(见图2a)，将流体域网格划分为瓣齿附近区域的旋转流体域(动网格区域)以及其外侧的非旋转流体域。

图2 密封结构内腔流体域和橡胶密封套网格划分Fig.2 Grid division of fluid domain in cavity of seal structure and rubber gland

网格划分采用多面体网格划分方法，由于各单元接触面更多，可以获得更多的插值信息，所以计算速度快且精度高，并且更适用于漩涡流的模拟。旋转与非旋转流体域交界面设定5层膨胀层，动网格设定旋转速度120、160和180 r/min。橡胶密封套为小端固定约束，大端施加轴向力，内腔中施加动压分布载荷。

2.2 数学模型

2.2.1 动网格控制方程

在正常工作时，由于花键在密封结构内部始终处于匀速旋转状态，所以本文选择守恒型的动网格流场计算方程[14]，其对应的控制方程如下：

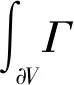
(1)

式中：V(t)为控制大小和形状随时间动态变化的控制体体积，m3；ρ为流体密度，kg/m3；φ为速度矢量；∇为散度；A为过流面积，m2；∂V(t)为控制体的运动边界；ug为动网格的运动速度，m/s；u为流体的流动速度，m/s；Γ为耗散系数，Pa·s；Sφ为φ的源项，Pa/m。

2.2.2 流体控制方程

流体连续性方程和动量守恒方程如下：

(2)

(3)

选择计算精度和计算效率较高的标准k-ε湍流模型[15-17]模拟内部流体的旋转流动，其中k和ε控制方程如下：

(4)

(5)

式中：ux、uy、uz分别为X、Y、Z方向的速度，m/s；p为流体微元体上的压力，MPa；t表示流动时间，s；τ为在黏性力作用下，流体微元体所受到的黏性应力，MPa；f为上述各个方向的单位质量力，N/kg；其中下标i表示沿着X、Y、Z方向的分量；k为湍动能，m2/s2；ε为湍动能耗散率，m2/s3；νt为黏性系数，m2/s；νt=ut/ρ，ut=Cuρk2/ε；ut为湍流黏度，Pa·s；C1、C2、Cu、σ1、σ2为上述模型的计算系数。

2.2.3 固体控制方程

(6)

式中：Ms为质量矩阵，kg/mm；ξs为阻尼矩阵，Pa·s/mm；Hs为刚度矩阵，Pa/mm；r为固体域的位置，mm；σs为密封套所受到的应力，MPa；ds为密封套所产生的位移，mm。

2.2.4 流固耦合方程

在密封套内腔中的流体与密封套在交界面处应满足守恒方程[18-19]，具体如下：

(7)

式中：τs为密封套的应力，MPa；τf为密封套腔体内部流体的应力，MPa；df为密封套腔体内部流体域所产生的位移，mm；nf、ns分别为固体和液体在耦合边界层处的法向矢量；Ts、Tf分别为密封套与其腔体内部流体交界面处固体表面和流体表面的温度，℃。

2.3 仿真结果分析

2.3.1 内部流场分析

图3为流体域的速度矢量图和流线图。其中X、Y为径向方向，Z为轴向方向。从图3可以看出，以Z轴为旋转中心，流体域产生了明显的涡旋流动。这是因为上接头将动力传递给中间轴，带动瓣齿高速旋转并对周围流体产生剪切作用，使得流体产生涡旋流动。在瓣齿所在内腔中的高速旋转流体会进入密封套中，并对密封套的内表面产生一定的动压作用。

图3 瓣齿所在内腔流体的旋转速度矢量与流线Fig.3 Rotation speed vector and streamline of fluid in the cavity

图4为不同转速下流体的速度大小与动压的分布规律。从图4可以看出，流速和动压较高的区域主要集中在瓣齿附近的旋转流体域，并且在转速一定时，靠近外侧的流体涡旋半径更大，旋转速度更高。同理，旋转流体域中的动压分布为外侧高、内侧低，并且在瓣齿的外侧曲面上产生的动压更高。随着旋转流体的转速从60 r/min逐渐增加至180r/min时，流速的峰值从49.3 m/s逐渐升高至148.0 m/s，动压峰值从0.84 MPa增大至14 MPa。由于靠近旋转流体域的外侧动压和旋转速度高，峰值主要集中于最外侧区域。因此，当旋转流体进入密封套后，在其径向方向上，靠近内表面区域的动压和流速高，靠近旋转中心区域的动压和流速相对较低。

图4 流体域的速度大小和动压分布Fig.4 Velocity and dynamic pressure distribution in fluid domain

以图4中120 r/min条件下的计算结果为例，对旋转流体域的速度和动压分布规律进一步研究。图5为旋转流体域中沿着径向方向的速度和动压分布。从图5a可以看出，流体域的速度分布在径向方向上以X轴或Y轴呈轴对称分布。以旋转中心为原点，随着半径的逐渐增大，流体速度逐渐升高，速度分布区间为60～100 m/s。

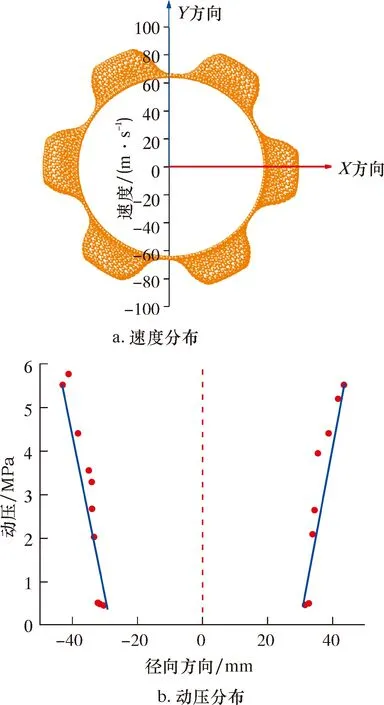
图5 旋转流体域径向方向的速度和动压分布Fig.5 Velocity and dynamic pressure distribution of rotary fluid domain in radial direction

由图5b可知，动压在径向方向上总体呈现对称分布，且距离旋转中心的距离越大，其涡旋流动速度越高，动压也逐渐增大，总体变化范围为0.5～5.5 MPa。

2.3.2 最大位移与变形量分析

为了进一步探究密封腔内流体所产生的动压以及马达转子轴向拉力对橡胶密封套最大应力和变形量的影响规律，以不同转速下所获得的动压计算结果作为橡胶密封套内腔中的分布力载荷，同时设定轴向力为20～100 kN进行分析。在橡胶密封套的小端(卡箍处)设定固定端约束，大端施加上述轴向载荷。计算得到如图6所示的不同动压或轴向力条件下的最大位移、最大应力以及最大位移相对变化率。

图6 不同动压和轴向力条件下最大位移、最大应力和变形量相对变化率曲线Fig.6 Relative change rates of maximum displacement，maximum stress，and deformation under different dynamic pressure and axial force conditions

如图6a所示，当轴向力一定时，随着动压从1.5 MPa逐渐增加到14.0 MPa，最大位移和最大应力都逐渐增加，其产生的变形量与初始尺寸相比，相对变化率从9.68%增加至10.45%。

如图6b所示，当动压一定时，随着轴向力从20 kN逐渐增加至100 kN，最大应力、最大位移和变形量相对变化率逐渐增大，其中变形量相对变化率从16.39%逐渐增大至18.15%。综合对比可知，轴向拉力所引起的变形量大于径向方向的变形量。

为了进一步探究橡胶密封套在综合载荷作用下的最大应力和最大变形量分布区域，现以0.5 MPa动压和20 kN拉力为例进行分析。图7为密封橡胶套的位移和应力分布云图。从图7可以看出，最大变形量主要集中于密封套中间区域，其最大应力主要集中在卡箍的固定区域。这是因为橡胶密封套小端被卡箍在径向上锁紧，在受到轴向拉力的作用下，最大应力主要作用于固定约束端处(卡箍所在区域的外表面为最大应力分布区)。在内腔动压作用下，橡胶密封套小端在径向上被卡箍锁紧，所以产生的变形量较小；同理，大端在轴向拉力作用下，在轴向上产生拉伸变形，从而导致径向直径减小，然而动压分布力作用下，径向会产生膨胀导致直径增大，大端的变形量相对较小，所以径向上在橡胶套中间区域产生的鼓胀变形最显著。

图7 0.5 MPa动压和20 kN轴向拉力下的变形量和应力分布云图Fig.7 Deformation and stress distribution diagram under 0.5 MPa dynamic pressure and 20 kN axial tension

2.4 现场试验

由仿真计算结果可以看出：橡胶密封套在卡箍处产生应力集中，容易导致密封套破损；在内腔中受到内压的作用且在中间区域容易产生鼓胀变形。为了对密封套的仿真结果进行验证，以焦页165-2HF井的1 502～2 591 m井段进行现场测试。参数如下：排量63～70 L/s，转速65 r/min，机械钻速5.08～17.16 m/s，钻压范围120～200 kN，扭矩12～24 kN·m。

利用上述参数进行现场测试，得到如图8所示的测试结果(密封套出现鼓胀变形和破损区域分布)。

图8 密封套鼓胀变形和破损的区域分布图Fig.8 Distribution of the bulging deformation and breakage areas of gland

从图8可以看出，橡胶密封套产生明显鼓胀变形的区域位于小端和大端的中间区域，而产生破损的区域主要是从卡箍处产生裂纹源，随着周期性的轴向力作用，裂纹逐渐增大导致小端出现破损。通过现场测试结果与仿真结果对比，验证了仿真结果的准确性以及橡胶密封套产生的失效机理。

3 结 论

本文首先对密封瓣齿式万向轴的总体结构和原理进行了介绍，然后基于动网格方法开展了橡胶密封套的流-固耦合分析，研究了密封结构内部流场的速度与动压分布，以及橡胶密封套位移与变形量的分布规律，并开展了现场测试，获得如下结论：

(1)在瓣齿高速旋转剪切作用下，密封结构内部流体会产生明显的涡旋流动，流体速度和动压以旋转轴为中心呈对称分布且距离中心距离越大，动压和旋转速度越大。

(2)瓣齿式万向轴的橡胶密封套主要承受内部流体的动压和轴向拉力作用，随着动压和轴向拉力增大，其最大应力和变形量都逐渐增大且轴向拉力对变形量的影响大于动压所产生的影响。

(3)综合流-固耦合仿真和现场试验结果，橡胶密封套承受轴向拉力导致橡胶密封套小端(卡箍处)产生应力集中，进而易导致破损；其内腔中流体动压的作用，使得中间区域更易鼓胀变形。该研究阐明了橡胶密封套产生密封失效的机理，可以为密封结构优化设计提供一定的参考，有利于延长瓣齿式万向轴的使用寿命。