基于与异或非图的混合粒度可重构密码运算单元设计

戴紫彬 张宗仁*② 刘燕江 周朝旭 蒋丹萍

①(解放军信息工程大学 郑州 450000)

②(31642部队 临沧 677000)

1 引言

信息安全在互联网、物联网中越来越重要，而密码算法是保证信息安全的关键手段[1]。其中对称密码分为序列密码和分组密码，由于多种对称密码的基本编码环节具有相似性，适用于可重构实现[2]。

粗粒度可重构密码逻辑阵列(Coarse-Grained Reconfigurable Cipher logic Array, CGRCA)根据密码算法的计算特征，在高性能和高灵活性之间达到平衡，ANOLE[3]是面向分组密码的高性能流水处理架构，采用查找表(LookUp Table, LUT)和寄存器的方式实现序列密码算法中反馈移位寄存器(Feedback Shift Register, FSR)的状态更新，但支持的序列密码算法较少，性能不高。PVHArray增加了专用的非线性反馈移位寄存器(Nonlinear Feedback Shift Register, NFSR)处理电路和FSR，但其处理粒度基于字，在实现序列密码的单比特更新时，高位计算资源被闲置，同时阵列在处理分组密码时，专用NSFR电路基本闲置，硬件资源利用率较低[4]。文献[5]提出一种面向序列密码的混合粒度并行运算单元，兼容多种粒度的序列密码算法，同时采用并行抽取和流水线设计提高了密码算法的处理性能。该单元提升了CGRCA对序列密码的兼容性，但仍然增加很多专用FSR的电路，硬件资源利用率低。文献[6]提出了一种可重构多发射流水处理架构，但是这种架构容易产生流水线的结构冲突，从而极大程度上限制了粗粒度可重构逻辑阵列的性能。综上，现有的面向对称密码算法的CGRCA，对序列密码兼容性较差、资源利用率低。

目前，国内外针对FSR进行一些可重构设计。徐光明等人[7]提出一种基于LUT的可重构NFSR处理结构，基础模块是支持任意6变量布尔函数的高级非线性逻辑单元(Advanced Nonlinear Logic Unit,ANLU)，该单元灵活性高，配置量少，硬件开销小，但性能和硬件资源利用率仍然较差。Nan等人[8]提出将NFSR、线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)和有限域乘法相融合的可重构单元，提升了硬件资源利用率。文献[9]以提高资源利用率为目标，以变量频次为约束改进适配算法，并设计单元互联结构，将资源利用率提高到91%以上。针对多功能融合的可重构单元，目前研究主要集中于对单一功能下的多种操作位宽设计的可重构[10,11]单元，以及用复选器进行功能重构的可重构单元。另外对于多功能实现往往是对单一功能的选择控制实现，流水线处理时会面临同一时刻要使用同一功能单元的情况，而此时，必然会有大量未使用功能单元闲置，功能单元的竞争冲突会同时带来性能和资源利用率降低。因此，设计可重构的多功能混合粒度的运算单元是解决细粒度的序列密码算法兼容性差，和流水线处理时功能单元竞争冲突问题的可行方案。

综合分析序列密码和分组密码中不同编码环节特点，分析得出电路同构部分，结合与-异或-非图(And-Xor-Inv Graph, AXIG)在逻辑综合上的优势，主要做出以下3个方面贡献：(1)提出可重构逻辑元件(Reconfigurable And-Xor-Nand, RAXN)，该元件可用于AXIG，可同时实现3项基本逻辑功能。另外，提出了RAXN的晶体管级方法并设计了版图，延迟性能较传统方法均有明显提升。(2)提出基于RAXN逻辑元件的多功能扩展方法，设计了多功能单元节点—RAXN-U，可重构实现全加器、3输入与异或逻辑、乘法部分积生成、可重构非线性布尔函数等功能节点。(3)提出一种面向粗粒度可重构阵列的可重构单元的互联结构，在CGRCA平台上可用于实现32 bit加法、8 bit乘法、CF(28)有限域乘法、非线性布尔函数等多项核心运算。

所提运算单元较为规整，可扩展性较强，非线性布尔函数的扩展只需改变互联节点配置，其他功能只需要增加少量控制电路，即可满足序列密码算法和分组密码算法的多种功能运算和多种位宽的需求。此单元将非线性布尔函数功能的延迟降低了1.27 ns，同时可以缓解电路资源闲置问题以及流水线处理时部分功能单元竞争冲突问题。

2 基于AXIG的可重构逻辑元件设计

2.1 AXIG理论与研究动机

逻辑综合是数字电路设计中非常重要的部分，选择不同的逻辑表达范式，综合优化后的电路在面积、性能、可测试性和可靠性上会有较大差别[12]。由于CMOS电路在可靠性、静态功耗以及设计复杂度等方面拥有显著优势[13]，传统布尔逻辑(Traditional Boolean, TB)得到广泛运用。而以And-Xor为原语的里德穆勒(Reed-Muller, RM)逻辑设计电路，可以使实现算术运算和奇偶校验函数更为简单，在面积、延迟和功耗上都有明显的优势。但用RM逻辑表达“或(OR)”逻辑时，需要较复杂的结构，因此和RM逻辑混合的AXIG有更大的优化效果[14]。目前针对AXIG的研究主要是在逻辑级或算法级对电路进行面积、延迟和功耗的优化，在晶体管级研究较少，文献[15]设计了基于RM逻辑的3输入AND/XOR门，在面积、功耗上相比传统的AND门-XOR门级联结构有明显优势，将该复合门运用到操作位宽可配置的乘法电路中，功耗和延迟有较大提升，但未有相关研究在晶体管级设计实现AXIG的基本单元。

本文设计一种可配置实现“与、异或、与非”逻辑的元件RAXN，其中AXIG中的“非(Inverter,Inv)”原语可以利用“与非”逻辑得到，因此可以根据需求，将RAXN作为基本逻辑单元，配置成为最优的AXIG，以充分利用其在复杂非线性布尔函数和算术电路中的优势。

2.2 RAXN逻辑元件晶体管设计

当M=0, C=0时，F=1。电路中Y和F的逻辑表达式分别如式(1)、式(2)所示

同时将信号M，或者A, B, C中的一个信号当作配置信息时，输出F可同时实现“And, Nand,Xor”，此3个逻辑正是双逻辑范式最基本的3个原语(And, Inv, Xor)。

2.3 RAXN逻辑元件延迟分析与版图实现

由图1可知，M=1, C=1，当电路输出为“Xor”逻辑时，若B=1, P1, P4, P5均是关断状态，则前一级上拉电路无法形成通路，N2, N3, N4均是导通状态，前一级下拉电路中形成如图1红线所示的信号通路。Y此时输出为0，则后一级中P9导通，N7关断；又因为此时P7, P8, P10是关断状态，N6,N7, N10是导通状态，则此时电路相当于信号A的反相器，A的翻转信号传到F需要经过P6, P9或N10, N8, N6(紫色线路部分)。若B=0，同理分析可得，A的翻转信号需要经过P5, N7到F，或者经过N5, N2, P9到F，即下降沿经过2个晶体管，上升沿经过3个晶体管。同理可得如表1所示为每个信号的翻转时信号传输路径。C的信号传输路径最短，B,A的最差情况一样长，但A的平均信号传输路径比B短。

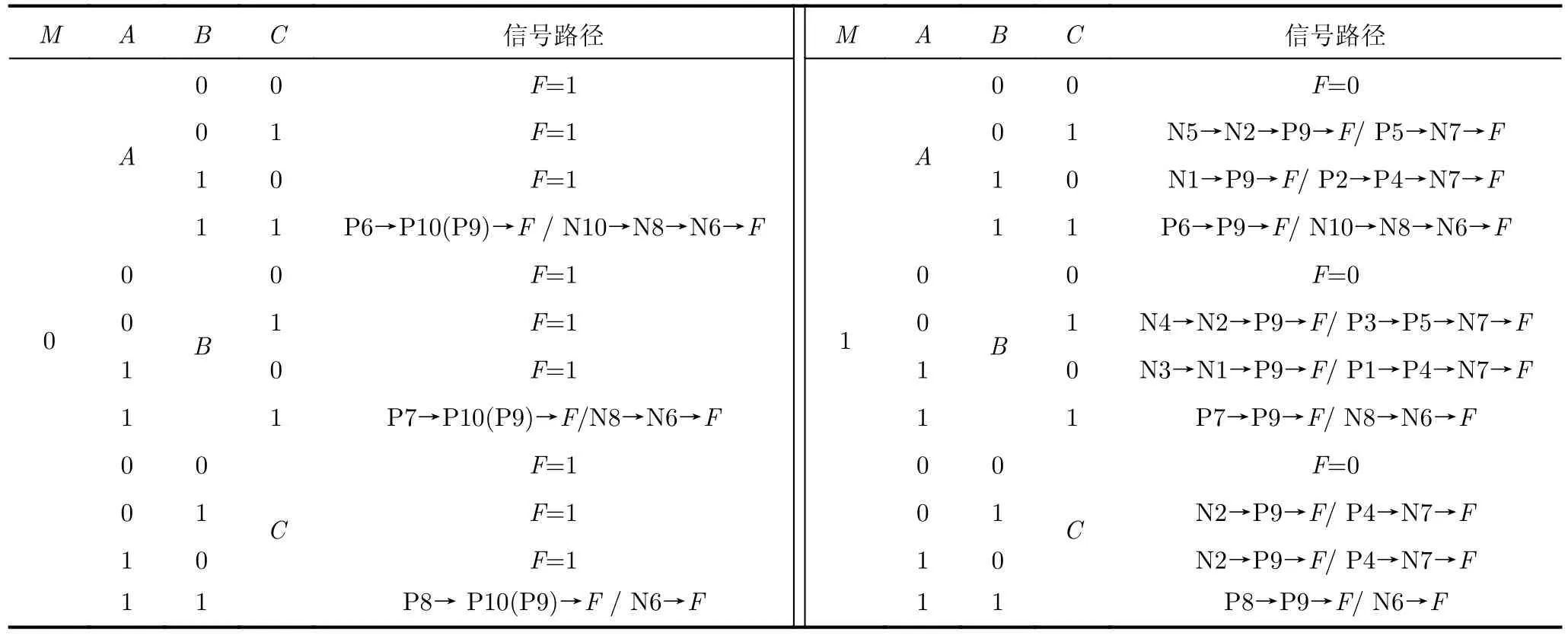
表1 RAXN电路信号传输路径分析

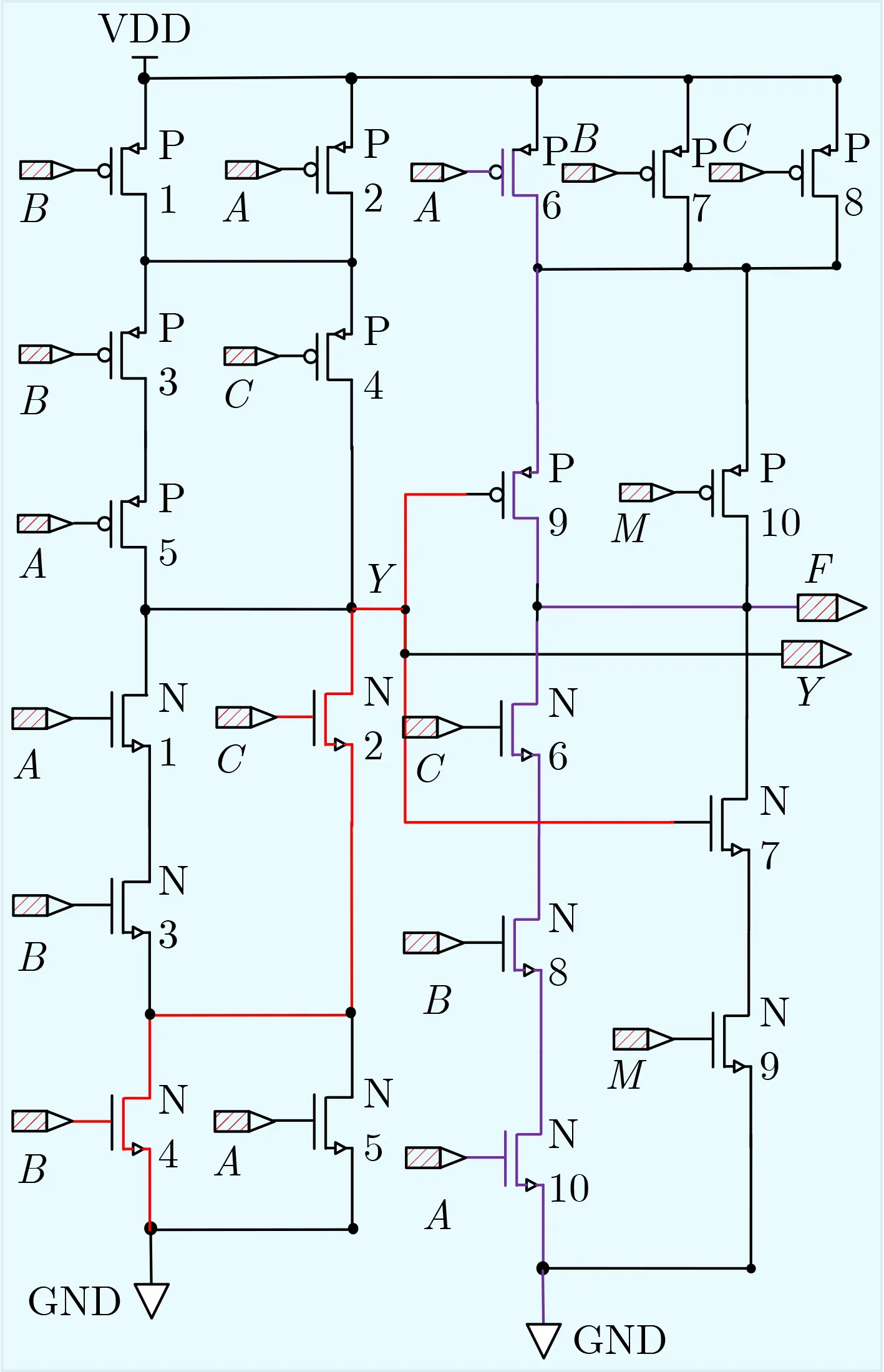
图1 RAXN晶体管级实现

根据以上分析，关键路径的信号从C端口输入时可以减少电路延迟，同时调整关键路径上的晶体管宽长比P5, P9, P10, N1, N2, N6, N7，减小单元的延迟。对于非关键路径上的晶体管可以采用高阈值的晶体管，以降低功耗，图2为其最小驱动能力下的版图设计。

图2 RAXN的版图设计

3 基于RAXN的密码运算单元分析

3.1 密码算子特征分析

对称密码算法是基于特定的密码学性质而设计的，因此不同的对称密码算法具有相同的基本操作成分，其中出现频次出现最多的是：异或、移位、置换、非线性(线性)布尔函数、S盒、有限域乘法和算术运算。

从本质上讲，所有的编码环节都是布尔函数操作，布尔函数又各有特点，比如序列密码中单比特为操作位宽的非线性(线性)布尔函数，特点是输入变量多，形式复杂多样；以字为操作位宽的序列密码和分组密码中S盒、置换、移位为多输入多输出，输入多为8, 16, 32等字节的倍数，输出有4, 8, 16等特定位数，有限域乘法主要集中CF(28)上，多以矩阵乘法形式出现，算术运算在密码学中使用模加、模减、模乘，位宽主要为16 bit和32 bit。因此设计一种位宽为8的基本单元，利用CGRA中数据抽取和数据分配电路，扩展至16, 32等位宽，同时实现多类操作，可极大提高资源利用率和单元的灵活性。本文重点讨论非线性布尔函数(S盒)、有限域乘法、算术运算这3类算子如何重构到同一单元中。

3.2 基于RAXN的3类密码算子设计分析

目前，对非线性布尔函数和S盒的研究主要是利用LUT的级联组合来实现，但LUT的灵活性过强，在特定领域中应用时会造成比较大的资源冗余[16]。2012年，瑞士联邦理工学院提出一种基于“与非锥(And-Inv-Cones, AIC)”的布尔函数实现方式，在处理大位宽输入的函数时有较为明显的面积和延迟优势[17]，但其“And-Nand”并不适合处理“异或”运算，针对密码学中非线性布尔函数异或逻辑较多的特点，本文提出一种“与-异或-与非锥(And-Xor-Nand Cones)”的网络(如图3)，节点采用本文设计的可重构逻辑元件RAXN，其中上一级输出接入下一级的A, B端口，C, M端口分别接配置信息di,di+1，输出端口F输出信号O，作为下一级的输入和全局输出。每个节点可以配置为“And,Nand, Xor, 1”4个逻辑，可以更好地支持“异或”运算；当第3级的一个输入端口需要置1时，只需将第2级相应节点的配置信息di,di+1全部置0即可，这样此节点的上一级节点仍然可以独立执行功能，避免了一条完整分支全部置1造成的资源占用。

图3 “与-异或-与非锥”3级深度的互联结构

有限域乘法主要出现在分组密码中多维尺度变换(Multi-Dimensional Scaling, MDS)矩阵乘法，序列密码算法中Fibonacci LFSR并行更新、Galois LFSR并行更新，以及基于字的序列密码中复合域乘法等编码环节中。相关研究总结出CF(28)域上乘法的基本电路结构，由两级运算电路，一级为幂乘(Xtime)电路，一级为“与-异或”的阵列[6]。“与-异或”的阵列可以用图3结构实现，Xtime结构是由3输入函数FX=hf ⊕a级联组成。其中f[7:0]是不可约多项式的系数，a[7:0]和b[7:0]是CF(28)域上的两个元素，若A=M=a,B=h,C=f，则根据式(5)可利用RAXN作为FX的实现电路

4 基于RAXN的可重构多功能密码运算单元设计

4.1 运算单元的整体布局

根据3.2节的分析，乘法电路和Xtime电路都需要8列7行的RAXN单元级联，而以8 bit行波进位加法器为基础的32 bit选择进位加法器，同样需要8列7行的RAXN单元。本文提出一种可以同时实现无符号8 bit乘法、CF(28)域乘法、32 bit选择进位加法、最大深度为8的“与-异或-与非锥”可重构混合粒度多功能密码运算单元(RHMCA)。如图4为单元整体布局，基本单元命名为RAXN_U，其中横黑线为加法的进位信号，竖黑线为输出信号，红线配合上级最后1 bit进位，是无符号8 bit乘法信号传输，P0为部分积；红线配合黄线是CF(28)域乘法的信号传输，蓝色线为“与-异或-与非锥”的信号传输。第2～6行的左4列不同于右4列，左4列每个单元多出两个外部数据端口。

图4 混合粒度多功能密码运算单元

4.2 多功能实现与单元扩展

如图5，在RAXN基础上增加模式选择电路、各模式下信号转换电路。图5(b)中F, G为模式选择信号，ai,bi,di,di+1可为数据输入信号，也可为配置信号，S信号为上一级输出，C为加法进位信号。当F=1,G=0,di=0,di+1=1 ，ai,bi为数据输入，此时执行加法，如图5 中红色线路；当F=1,G=1,di=0,ai为 乘数，di+1为被乘数中1 bit，同一行的di+1相同，bi为任意值，此时执行乘法运算；F=0,G=1,ai=1,di+1=1，di为不可约多项式系数，此时执行有限域乘法运算，如图5中紫色线路；当F=0,G=0,ai=1,bi=1,di,di+1为配置信息或输入数据，此时执行非线性布尔函数。

图5 RAXN_U电路结构

本文设计单元可以直接得到7个8 bit行波进位加法器、1个无符号位的8 bit乘法、1个Xtime的功能实现。接下来重点分析复杂非线性布尔函数实现能力、扩展方式，以及高位宽扩展实现方式。

(1)灵活性。文献[5]对CGRA在面向序列密码时的互联结构进行设计，利用其中的抽取电路，可以将所需的变量送入到相应位置。根据需求，送入的变量可以是反相，每个RAXN_U可以实现任意的二输入布尔函数。除了“And,Xor,Nand,1”4种逻辑，在需要“Or”逻辑时，A,B输入同时取反，节点逻辑配置为Nand，需要“Xnor”逻辑时，将输入取反，节点逻辑配置为“Xor”。每一行左4个单元A,B端口不接上级输出，可以接收外部输入，那么本文所提出单元最高可实现72次的乘积项，或56变量的异或。第1行的输入变量在第3行可以与第2行左4个电路输入的变量进行运算，当第6级需要外部变量参与运算时，就可以将相关变量从第4级输入，这样避免了锥形结构中为实现直通功能造成的大量资源浪费。

(2)扩展能力。当1个单元无法实现复杂的函数功能，可以通过图4中Ie的信号实现单元之间的扩展。如图6所示，当不需要扩展时，红色块配置为逻辑“1”，那么每个单元可以独立运算；但当Toyocrypt-hs1算法中的反馈函数，需要3个本文所提单元，红色块配置成所需的“异或”逻辑即可。相比1个单元模块，每多扩展1个，延迟仅仅增加1个RAXN_U的延迟。

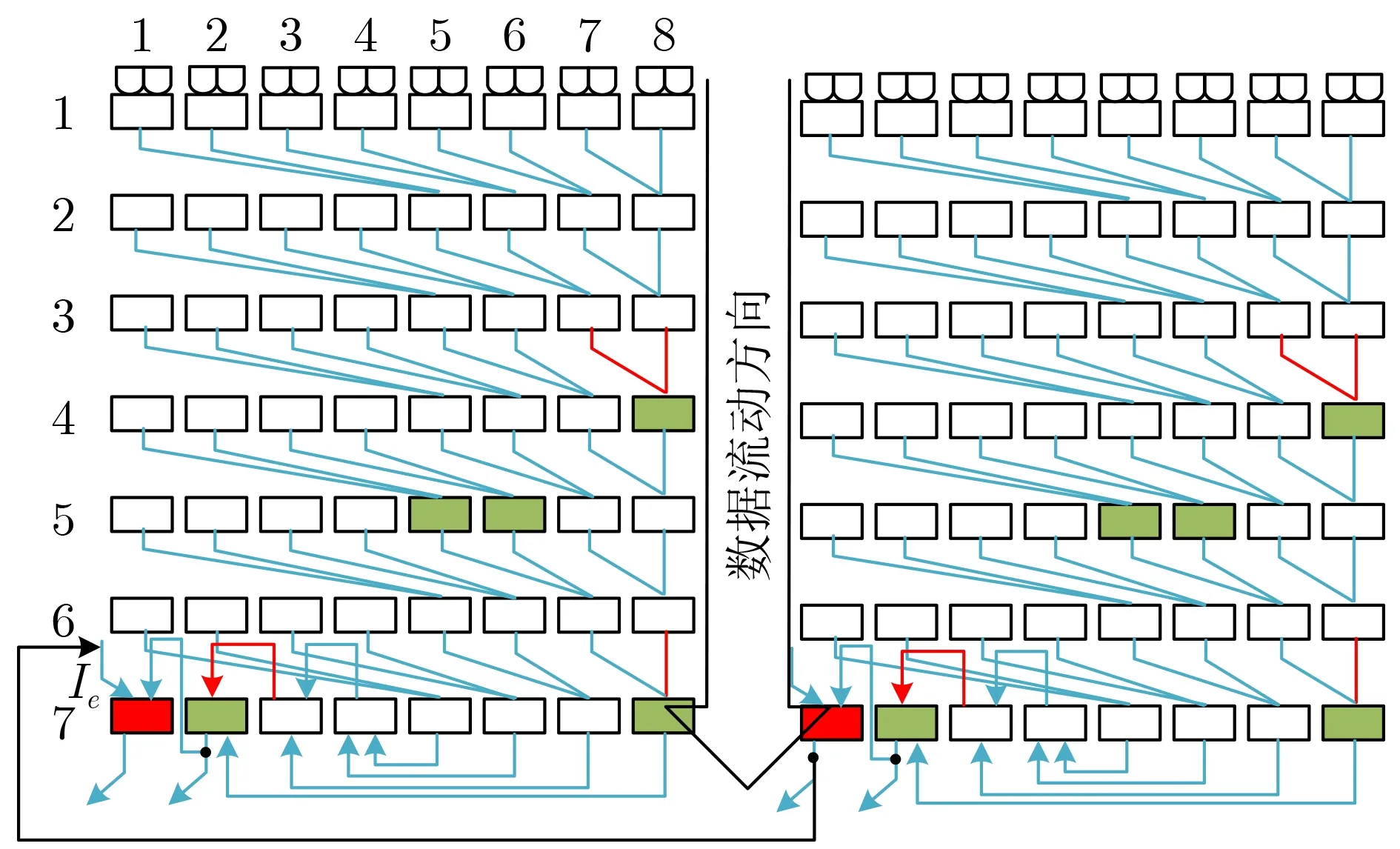
图6 单元扩展与拆分示意图

(3)单元拆分组合。利用外部互联网络中抽取电路有针对性地对所需的结果进行抽取，可以实现单元的拆分以及延迟可控及功能组合。如图5(a)所示，第1行每个RAXN_U中可以实现2个2次乘积项，以及1个RAXN功能。因此可以利用第1行实现两个Xtime的结果处理，则1个单元可以完成4个Xtime输出的处理，如图6绿色块配置为逻辑“1”，实现了单元内部的拆分，红线即为所需信号。在实现32 bit加法器时，第2行与第3行输入相同的数据，但初始进位信号不同，4, 5行、6, 7行同理为一组，根据选择进位加法器的原理，对输出结果进行抽取。

(4)乘法位宽扩展。有限域乘法进行位宽扩展时，只有在执行LFSR并行更新功能时，需要最左边输出信号替换其他扩展单元的左边第1个输出信号，参与下一级运算，单元间每一行增加1个2:1复选器。模乘位宽只用扩展到32 bit，且整个模乘运算在密码算法中仅有6.25%的使用率，不宜做特别改造。本文拟采用多周期实现位宽扩展。8 bit乘法结果为16 bit，区分为高8 bit (H)，低8 bit (L)，模乘运算一般只取低8 bit。在整个16 bit结果时，高8 bit的延迟约为整体延迟的1/3，因此将低8 bit全部生成的时间作为关键路径延迟(时钟周期)，可经过如图7所示5个时钟周期完成位宽的扩展。第1个周期，第2周期分别生成所有L,H，计算1对16 bit加得到sum0，1对24 bit加得到sum1，并输出out0；第3个周期，计算1对16 bit加得到sum2，计算1对24 bit加得到sum3, sum3低8 bit输出out1；第4,5个周期分别计算1对16 bit加得到sum3，1对8 bit加得到sum4，并分别输出out2, out3。

图7 32 bit模乘计算过程

5 实验及性能分析

在COMS 40 nm工艺，25°C, 1.1 V驱动电压，TT工艺角环境中，为使RAXN_U信号输出延迟最小，上升和下降沿尽量相同，调整晶体管的宽长比。对图5(b)电路的进行版图设计，经过布局布线和后端仿真，面积为26.9 μm2。根据连接关系，测得端口F的输出电容为5.1 fF，端口Y的输出电容为0.85 fF，遍历各种功能下的输入取值，得到如图8各种功能模式下翻转延迟分布。

图8 各功能模式下的延迟情况

实现加法功能时，关键路径在“进位到进位(C→C)”的延迟，最大值为44.4 ps，最小值为40.6 ps；乘法阵列功能时，关键路径在“加(和)位到进位(A(S)→C)”，“进位到和位(C→S)”与“进位到进位(C→C)”的延迟累加，其中“A(S)→C”的最大延迟为55.8 ps，最小值为43.5 ps，其差值为12.3 ps，“C→S”的最大延迟为59.3 ps，最小值为41.6 ps，其差值为17.7 ps。

实现Xtime功能时，关键路径是上级输出到此级输出，最大延迟为66.2 ps，最小值为36.7 ps，差值达到30 ps，不同取值情况延迟差别过大，会导致电路中出现不必要的翻转而增加延迟和功耗。从图8中E可以看到延迟集中在40 ～50 ps，仅有一种翻转延迟情况达到66.2 ps，远大于其他值，此情况下的翻转信号路径最长。把幂乘中扇出为8的输出信号-1，接入延迟信号较短的输入端口，大扇出导致驱动能力变弱，使最小延迟增大，缩小最大延迟与最小延迟的差值，经过实验仿真延迟差可以从30 ps降到14 ps。

实现非线性布尔函数功能时，最大延迟为70 ps，最小延迟为39.1 ps，延迟差为30.9 ps。延迟的中位数在58.7 ps，平均值在57.6 ps，说明整体延迟分布比较均匀。对于RAXN单元，从端口A,B,C进入的信号在功能函数中是等价的，因此将延迟差较为接近的两个端口A和B作为级间传递信号的输入端口，端口M和C的信号为外部输入，延迟差可以降为15 ps。

利用EDA工具调用CMOS 40 nm工艺库标准单元对本文所提出结构进行综合验证，和对本文多功能运算单元进行定制化设计后实验仿真，如表2所示是其两种实现方式下的不同功能延迟和总面积。

表2 两种方式实现下延迟和面积

根据文献[18]，对不同工艺下的延迟、面积进行归一化处理，得到如图9的对比结果。

图9 不同功能模式下性能和资源占用对比

如图9(a)是使用标准单元实现几种专用8 bit加法器的面积、延迟以及面积延迟积(Area-Delay Product, ADP)[19]，本文所提单元实现加法功能与类似的行波进位加法器延迟降低24.6%，大约0.13 ns，相比其最快的加法器结构延迟增加40.6%，约0.11 ns；图9(b)与传统阵列乘法器LP，可变操作数乘法器[10]，以及定制优化的乘法器[11]的延迟进行比较，在实现8×8乘法功能时，延迟最多增加15%，约0.14 ns，与用标准单元库实现几种不同结构下的乘法器[20]，比较ADP值，最高得到44.8%的优化；图9(c)为可重构NLBF运算单元比较，文献[9]可实现几乎所有序列密码中以1 bit为操作位宽的NLBF，本文最多需要3个本文所提单元即可达到相同功能，在一个RHMCA基础上延迟增加210 ps，面积增加2倍，与相关研究中最好结果RSCLU[9]比较，延迟降低1.27 ns, ADP值增加38.7%。结果表明，相比加法，乘法电路的专用电路，延迟最多增加0.14 ns，性能损失可接受；相比其他NLBF实现单元，延迟有大的提升，主要是由于AXIG在复杂布尔函数的优势[14]；由于有限域乘法单元在对幂乘单元设计基本结构相同，若使用标准单元实现，延迟约为0.610 ns，面积为427.3 μm2，ADP为260.653 μm2·ns，本文所提单元延迟降低6.6%，约40 ps，面积增大2.54倍，ADP增加231%。综上所述，本文由于是多功能可重构单元，与专用电路，延迟增加最大的是乘法功能时，增加0.14 ns，延迟优化最大是实现NLBF功能时，降低1.27 ns；单一功能下，实现乘法功能和NLBF功能占用面积相对较大，比较两种功能模式下的ADP值，本文所提多功能单元在乘法功能时有0.7%～44.8%的提升，在NLBF功能时有–38.7%～82.2%的提升。

6 结束语

本文提出一种混合粒度的多功能可重构密码运算单元，用于改善细粒度序列密码的兼容性和避免功能单元竞争冲突。该单元利用阵列中数据抽取电路和数据分配电路，可以实现非线性布尔函数，也可以作为S盒、模乘、模加和有限域乘法的实现单元，可以有效降低电路延迟，实现密码算子功能的可重构，系统级可重构的流水线设计和互联网络设计有更大的提升空间。针对本文所提单元，在算法映射、数据分配电路等方面还需要进一步研究。