面向存算一体架构中Tanh激活函数的绝对值电路设计

顾晓峰 管其冬 虞致国

(物联网技术应用教育部工程研究中心 无锡 214122)

(江南大学电子工程系 无锡 214122)

1 引言

随着集成电路制造工艺日趋成熟，芯片设计向着高速、低功耗、低面积的方向发展。但由于晶体管特征尺寸缩小受限，芯片的集成度已无法达到“摩尔定律”的预测效果，传统冯诺依曼架构也面临着功耗墙和存储墙问题[1]。至此，以存储器为核心的计算体系架构—存算一体(Computing In Memory, CIM)架构应运而生[2–7]，延长了“摩尔定律”的生命，打破了存储墙的瓶颈，扩大了神经网络的应用领域[8–13]。

典型的基于神经网络的CIM架构中，每一层的输入数据首先由线性向量矩阵乘法器处理，然后通过模拟生物神经元的激活函数引入非线性因素，激活函数可以实现神经网络输入与输出之间的非线性映射，使得神经网络能够逼近任何非线性模型中[14,15]，以解决线性模型的表达、分类能力不足等问题。而双曲正切函数Tanh的输入与输出均处在[–1, 1]之间，函数值变化敏感，能够保持非线性单调上升和下降关系，易于神经网络的梯度求解，容错性好，符合人脑神经饱和的规律。

基于CMOS工艺实现Tanh激活函数的方式包含模拟设计、数字设计以及模数混合设计，文献[15]将P, N型MOS管及电阻组成一个神经元电路，利用MOS管的饱和特性，通过基尔霍夫电流定律建立输入电流与输出电压函数关系，得到Tanh函数拟合曲线，该电路结构简单，但是电流变化，影响MOS管工作范围，且电流输入，会产生电荷泄漏，影响电压输出；文献[16]提出另一种Tanh函数简单实现方式，利用PMOS管及NMOS管的导通特性，对固定电阻传输电流进行I-V转换，得到相应的Tanh函数曲线，其实现了电路的快速转换，但小电阻阻值需要大的电流，显著增加电路功耗，相反控制小的电流则需要大电阻阻值，给电路提供了额外的面积开销；文献[17]采用数字组合逻辑完成正半轴计算电路以及负半轴反射电路，利用Verilog语言对上述电路拟合实现Tanh函数，但一系列数字电路给系统功耗及面积同样带来了不小的开销。

与数字实现相比，模拟设计更快、更节能[18,19]。但是对于模拟设计而言，激活函数中Tanh函数负值处理难度较大，复杂度较高，且不易转化。为解决上述问题，本文基于CMOS工艺提出一种实现Tanh函数负值转化的高速、高精度、离散型绝对值电路设计，转化后的绝对值输出通过模数转换器(Analog to Digital Converter, ADC)、数字控制逻辑等模块将器件输出重新拟合成Tanh函数。

但是绝大多数绝对值电路都是依靠二极管全波整流来实现，由于二极管的非线性失真严重且很难集成，很难适用于大规模集成电路系统架构中。文献[20]提出一种电流模形式绝对值电路，利用P型电流镜以及N型电流镜不同的导通条件将正负输入电流以不同形式输出，实现绝对值电路功能，但是电流镜拷贝精度很难控制，且大的电流条件下增加了电路功耗；文献[21]使用两个比较器以及1个异或门实现绝对值比较电路，通过将输入电压绝对值化，再将输出值与0进行比较，异或后得到最终的比较结果，但是为了降低比较器延时，需要更大的电流，从而引入更大的电路功耗。

针对上述问题且满足实现存算一体架构Tanh函数离散信号运算处理的要求，本文设计出一种新型高速、高精度绝对值电路。整体绝对值电路由高速比较器、快速建立运算放大器以及部分开关组成。

2 Tanh函数的实现

图1展示了CIM的整体架构以及通过绝对值电路方式实现Tanh函数的过程，每一个存算单元为闪存(Flash)型存算器件。图1存算阵列内部每一列存算单元器件连接同一条字线(Word Line, WL)，源极(Source Line, SL)接固定电压，漏极连接同一条位线(Bit Line, BL)传递读出系统所需要的输出值。输入信息通过脉冲编码输入到WL上，当WL上信号是高电平时，在BL端会产生一个大小为

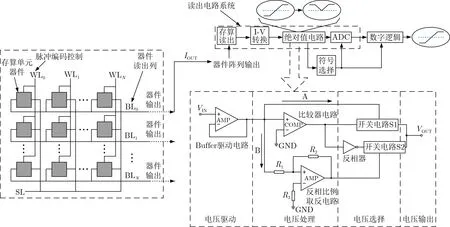
图1 CIM整体架构

的单位电流，其中，µ是存算器件的迁移率，Cox是其栅氧电容，W, L分别是其宽、长。当WL上信号是低电平时，不会产生电流，通过基尔霍夫定律，在BL端输出器件产生的电流流入读出系统的读出电路中进行放大、读出等操作后，经过I-V电路转化后电压传输给绝对值电路，符号选择电路可将绝对值判断的正负值存储并在ADC以及数字控制逻辑电路工作时发送。当绝对值电路数据处理完成后发送给ADC进行模数转化，并接收符号选择电路的正负信号进行传输，最后通过数字电路的内部逻辑将ADC的输出信号拟合成Tanh函数曲线。

3 绝对值电路架构及分析

3.1 电路整体结构

处理Tanh激活函数中负值的高速、高精度、离散型绝对值电路包含电压驱动的缓冲(Buffer)驱动电路，电压处理的比较器电路、反相比例取反电路以及电压选择的开关电路、反相器电路，其整体框架如图1所示。

存算阵列输出信号经过存算读出、I-V转换后传输给绝对值电路，此时绝对值电路中的比较器时钟在Buffer驱动电路输出电压稳定后开始比较(时钟处于低电平)，输入电压经过Buffer驱动电路后传输给比较器电路、反相比例取反电路以及开关电路S1，由比较器产生的结果判定后续开关是否打开，以此来控制输入电压的传输。当输入电压VIN为正值时，比较器输出结果为1，开关S1打开，VIN沿A支路通过开关电路S1传输出去；当输入电压VIN为负值时，比较器输出结果为0，经过反相器反相后，0变为1，开关S2打开，S1断开，输入的负压沿B支路经过反相比例取反电路后变为正压，再由开关S2传输出去，其传输公式如式(2)所示

由于CIM架构处理Flash器件阵列产生的某一固定信号值，因此比较器时钟在Buffer驱动电路输出稳定电压值之前一直处于高电平复位状态，直到电压稳定后比较器时钟才转换为低电平比较状态，为了适应ADC采样信号，因此比较器会在采样结束之前一直保持低电平比较状态。

3.2 Buffer驱动电路

绝对值电路中的Buffer驱动电路如图2所示，采用2级运算放大器对输入电压进行驱动跟随，将2级运放接成单位增益缓冲器的电路结构，使其能够稳定供给比较器，防止电压波动对后续传输产生影响。还需考虑其速度问题，尽量减小I-V转换到ADC之间的转换时间，提高整体运算速度。启动电路以及基准电流源构成2级运放的偏置电流供给模块。由于绝对值电路的输入会有负压，因此将2级运放的NMOS换成深阱(Deep NWell, DNW)工艺的NMOS，以使其能够更好地耐压。

图2 Buffer驱动电路

启动电路作为基准电流源的上电电路，必须满足上电以及自动关闭的功能。PM1为开关，当电源处在缓慢打开过程时，PM1导通，电源电压缓慢给MOS电容C1充电，此时PM2的栅源电压逐渐减小，慢慢达到PM2的阈值电压直至PM2截止，启动电路关闭。为避免A支路上的电压因PM2的传输产生波动，利用MOS电容C2电容对其进行稳压，以实现稳定输出电流。

为了提高基准电流源的电源抑制比，设计由PM3～5, NM1～3以及电阻R组成的负反馈结构基准电流源，使Buffer驱动电路能够更加稳定驱动输入电压。其中分压电阻R的选取一方面需要满足输出电流的精确输出值，一方面需要抵消基准电流源内部的温漂系数。最终基准电流通过电流镜拷贝沿B支路给2级运放提供稳定偏置电流。

3.3 比较器电路

比较器电路是为了比较输入电压与零值的大小，确定比较器后接开关是否打开，判定开关传输相应的电压值。单级的比较器即运放结构比较器，其精度较高，但是速度低，高精度是要求单级比较器有大的增益，但是却要牺牲带宽；锁存比较器可快速比较差分输入电压，但是精度偏低，且失调电压较大。

综合考虑比较器的速度，为了实现绝对值高速高精度的要求，采用两级预放大器加动态锁存器构成的比较器结构，其整体架构如图3所示。第1级预放大器需要将信号快速放大，因此需要更高的带宽；第2级预放大器则需要更高的增益来放大输入的差分信号，使得动态锁存器拥有足够的电压摆幅。因此设计采用电流镜负载的高带宽全差分运放，如图3(a)、图3(b)所示；第2级同样采用上述架构，并通过降低电压偏置适当提高其增益，放大差分输入电压值；动态锁存结构如图3(c)所示。

图3 比较器整体电路架构

为满足存算一体的高速算力要求，实现数据的快速传输，将绝对值电路的1个工作周期设置为50 ns，同样需要将比较器的时钟周期控制在50 ns以内，因此到达锁存器的比较信号至少要在比较器周期的1/2时间内达到稳定，根据输入信号延时求得预放大器的偏置电流大小

其中， ∆V为预放大器的输出共模电平，CL为负载电容。因此

根据式(3)可得

通过负载的大小可获得预放大器偏置电流最小值。

3.4 反相比例取反电路

为了实现相反数的运算功能，将架构外负输入电压转换为正输入电压供后续电路传输，设计如图4所示的反相比例取反电路。其中运算放大器(AMPlifier, AMP)同样是由上述Buffer驱动电路中的2级运放构成的，R1～R3组成反相比例取反电路的比例系数运算电阻。

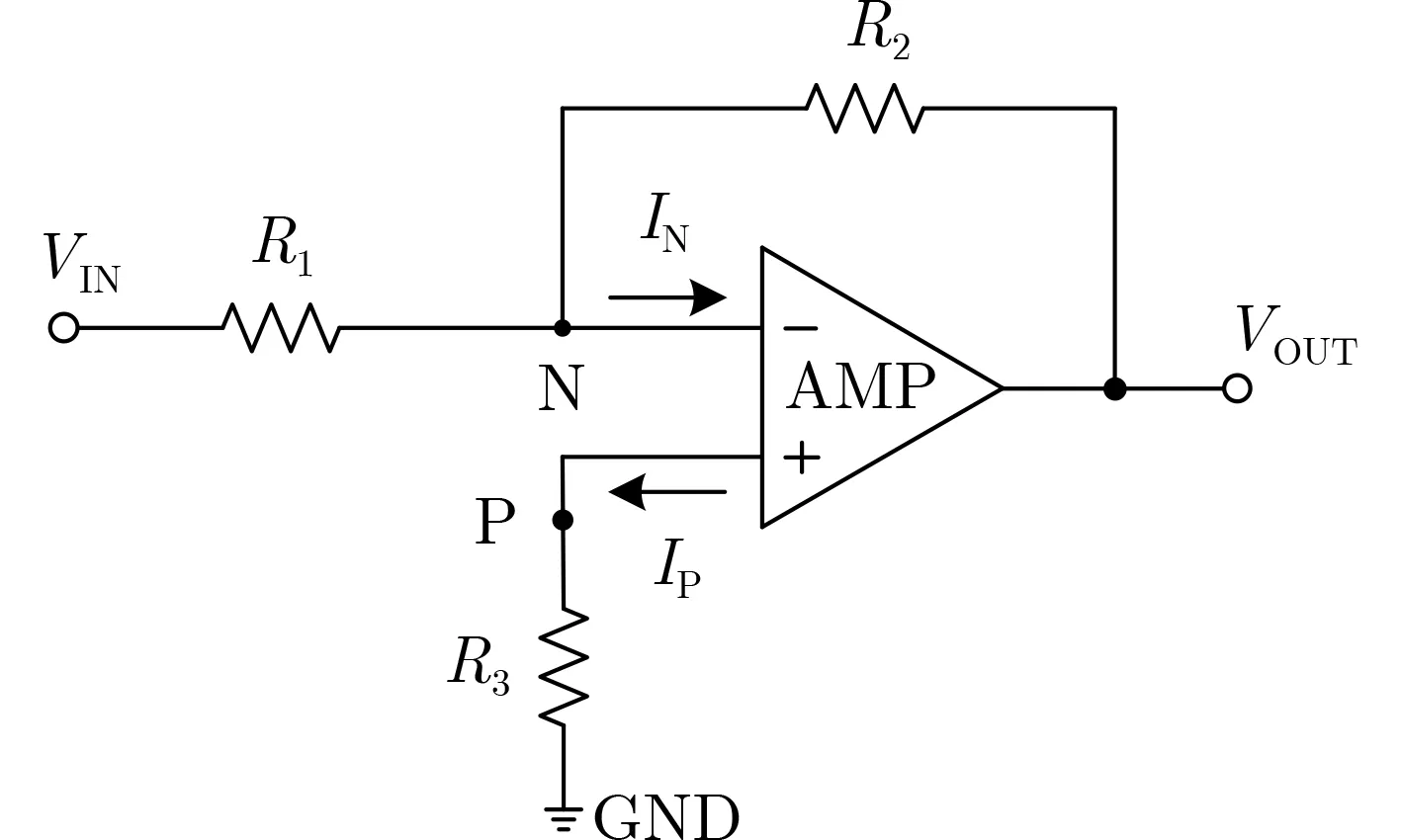
图4 反相比例取反电路图

3.5 开关电路

本文所提开关电路不仅要通过比较器的输出信号来判定开关是否打开，还要将处理的输入信号进行传输，因此采用如图5所示的产生互补时钟的传输门开关电路。比较器输出的高低电平经过PM1,NM1构成的恒导通的传输门以及PM3, NM3构成的反相器，一个正向导通，一个反相传输，信号经过传输门的时间可等效反相器的延迟时间，以产生互补的时钟信号，并通过PM2, NM2和PM4, NM4构成的反相器驱动，最终互补的时钟信号CLK,CLK用来控制PM5, NM5构成的传输门是否导通。

图5 产生互补时钟的开关电路

4 电路仿真及其分析

4.1 电路各个子模块仿真

采用55 nm CMOS工艺对新型高速、高精度、离散型绝对值电路进行电路设计，并对各个子模块主要关键技术指标进行仿真分析。由于CMOS器件单元易受工艺角、温度等条件的影响，因此主要针对以下3种PVT(Process, Voltage, Temperature)条件进行前仿：tt与25°C，ss与125°C，ff与–40°C。其中tt与25°C，ss与125°C，ff与–40°C分别为标准、最慢以及最快的组合条件。最后对整个电路架构进行相应的仿真对比分析。

仿真Buffer驱动电路驱动跟随稳定性，其结果如图6所示，输入电压在–100 mV和100 mV内来回切换，均在50 ns内达到稳定。其中深蓝色曲线为±100 mV参考电压值，浅蓝色曲线和绿色曲线分别为ss与125°C、ff与–40°C下电压的跟随状态，从图6可以看出，–40～125°C，工艺角从缓慢到快速变化，Buffer驱动电路的跟随稳定时间均能控制在50 ns以内。其在不同PVT条件下具体驱动稳定时间对比分析如表1所示。上述可以看出，Buffer驱动电路的前仿结果在对应的PVT条件下基本保持一致：较慢状态下建立的时间较长，较快状态下建立的时间较短，以保证在50 ns内数据能够稳定传输给后续电路工作。

图6 Buffer驱动电路建立时间

比较器整体瞬态仿真如图7所示，并对比较器在不同PVT条件下进行工艺角仿真。图7可以看出20 MHz频率下，比较器延时为5 ns，且比较器最低比较电压可精确至550 μV以内，满足低电压比较的要求。其在不同PVT条件下仿真的延时如表1所示。在ss与125°C和ff与–40°C条件下，比较器延时达到最长与最短，分别为10 ns和 3 ns。

图7 比较器瞬态仿真

图8为反相比例取反电路在标准状态下反相输入与反相输出仿真图，当输入电压从–100～100 mV离散变化(50 ns一个台阶电压变化)时，输出电压可以从100～–100 mV同比例反相变化，取反精度小于1 mV，误差小于1%。在不同PVT仿真条件下对反相比例取反电路进行功能仿真分析，其仿真分析对比如表1所示，在ff与–40°C与ss与125°C条件下，会出现最小误差与最大误差，分别为0.02 mV和1.04 mV。

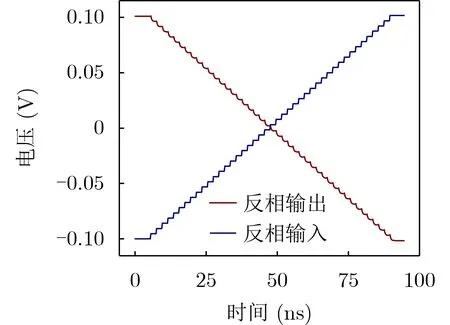
图8 反相比例取反电路功能实现

由上述分析数据可以推断得出，在ss与125°C状态下，温度升高，影响器件的载流子迁移率以及阈值电压，从而改变了MOS管之间的导通电压，继而影响了反相比例取反电路的运算输出。

传输门开关需要与比较器输出信号同步，尽量减少延时，图9为传输门开关在不同PVT条件下针对输入电压从–100～100 mV台阶变化后的输出曲线图。不同PVT条件下的输入信号经过开关电路均能够很好地输出。

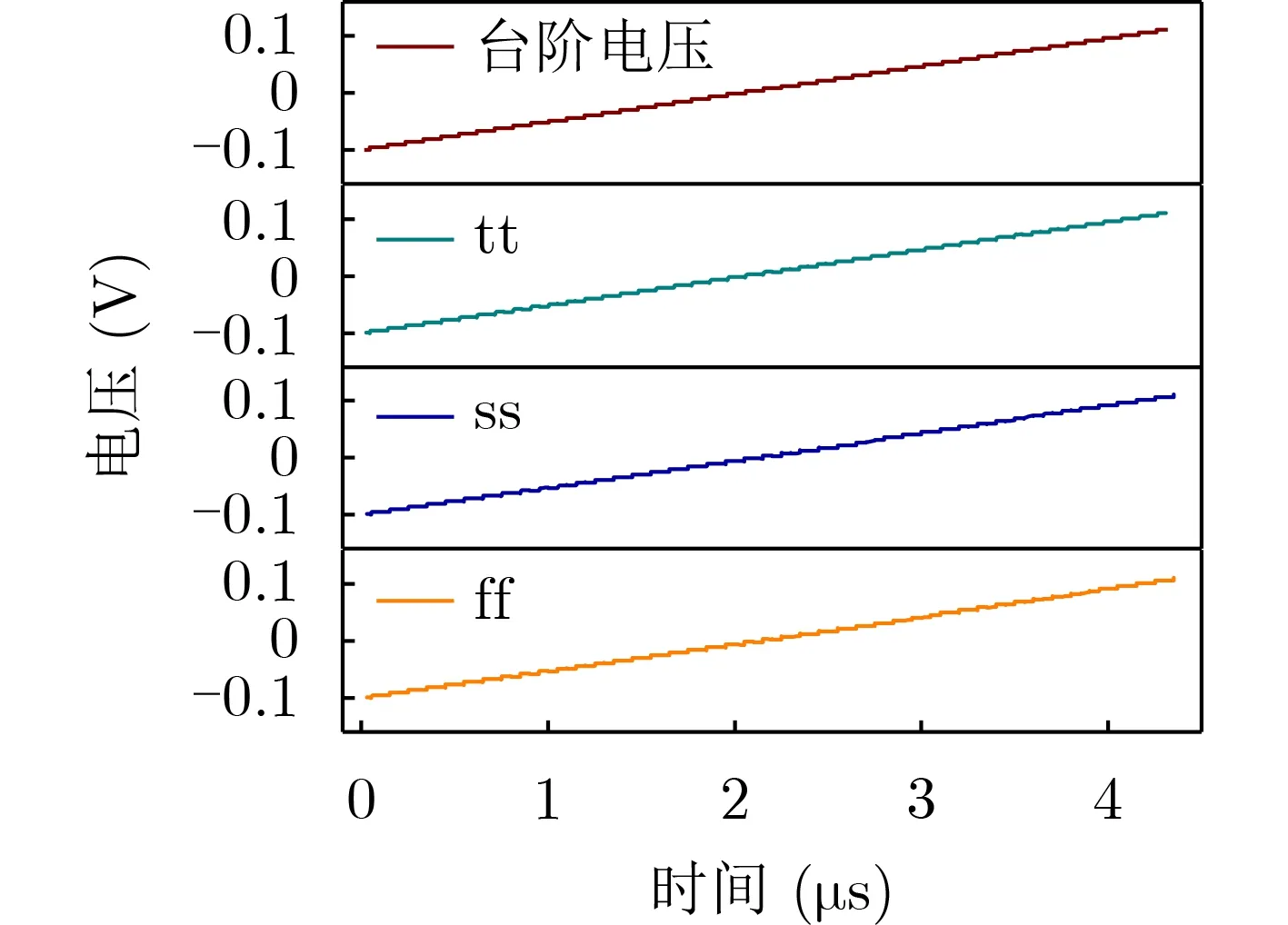
图9 传输门开关在不同PVT条件下的输出曲线

4.2 整体电路架构仿真及其对比分析

图10为绝对值电路过零点区域放大的电压值，其在不同PVT条件下零点电压值均在400 μV以内，通过对零点电压放大观测，确定该绝对值电路在零点处的偏移误差性很小，保证以零值为中心点的左右正负值能够很好跟随。

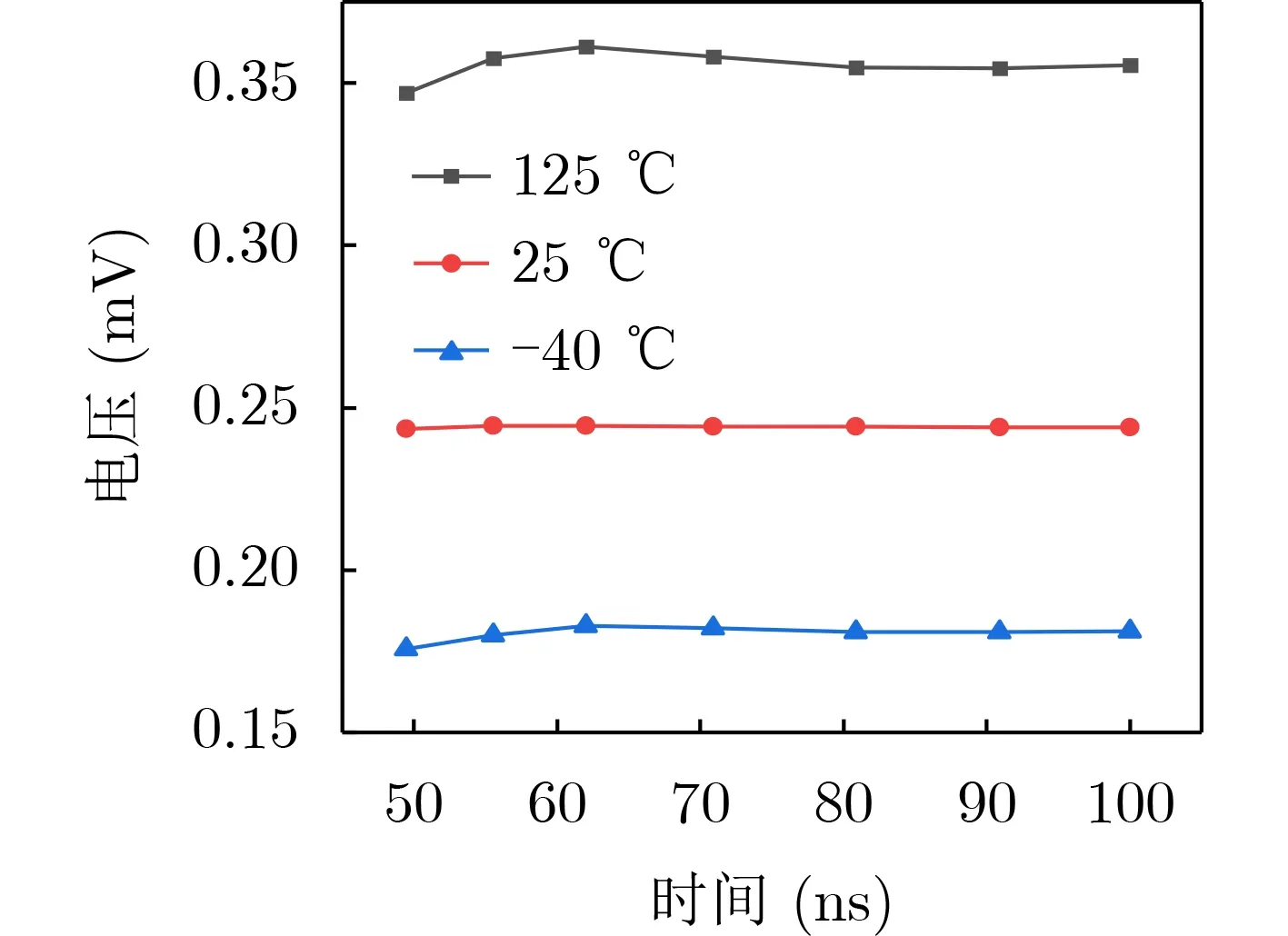
图10 绝对值零点放大

存算阵列在每一个数据读出周期下均是固定值，经过读出电路稳压放大操作传输给绝对值电路，因此，绝对值需处理每一次读出的正值或者是负值。图11为绝对值整体电路架构以50 ns为1个周期，从–100～100 mV的台阶电压变化下的仿真图。图11可以看出，一个周期内的绝对值转化误差都控制在1 mV以内，其在不同PVT条件下的误差大小如表1所示，在ss与125°C与ff与–40°C条件下误差达到最大和最小，分别为1.12 mV和0.69 mV。通过将台阶电压变为拟合的正弦波信号对该绝对值电路再次进行仿真，得到如图12所示波形，图12中，正弦波正半轴电压原值输出，而在负半轴，由于比较器的复位阶段，部分负压保持，而在比较阶段的负压能够很好地转化为正压，具有很好的拟合性，满足了固定周期内实现存算阵列输出值的相应转换。

图11 台阶周期电压仿真曲线

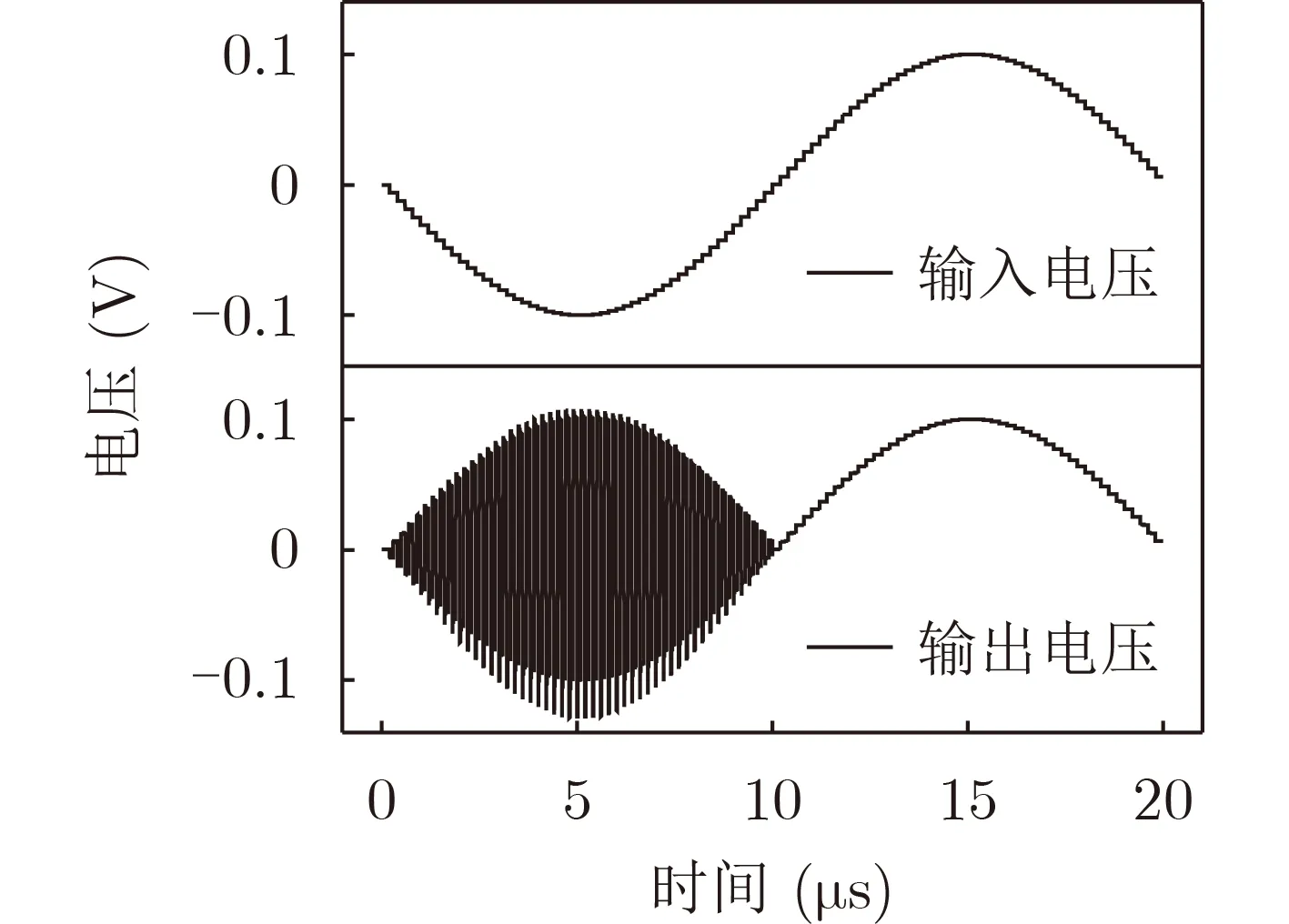
图12 正弦周期电压仿真曲线

图13为绝对值电路输出电压与输入电压之间差值分析的蒙特卡罗柱状图。图13中，蒙特卡罗正态分布一个σ的值约为0.6 mV，3σ值约为1.8 mV，平均电压值为–0.2 mV。绝对值电路的随机失调误差大致分布在–1.5～1 mV。可以看出，输入电压在经过整体绝对值电路转化后，绝大部分输出值误差均小于1 mV，小部分电压略大于1 mV，实现了该电路高精度的转化特性。

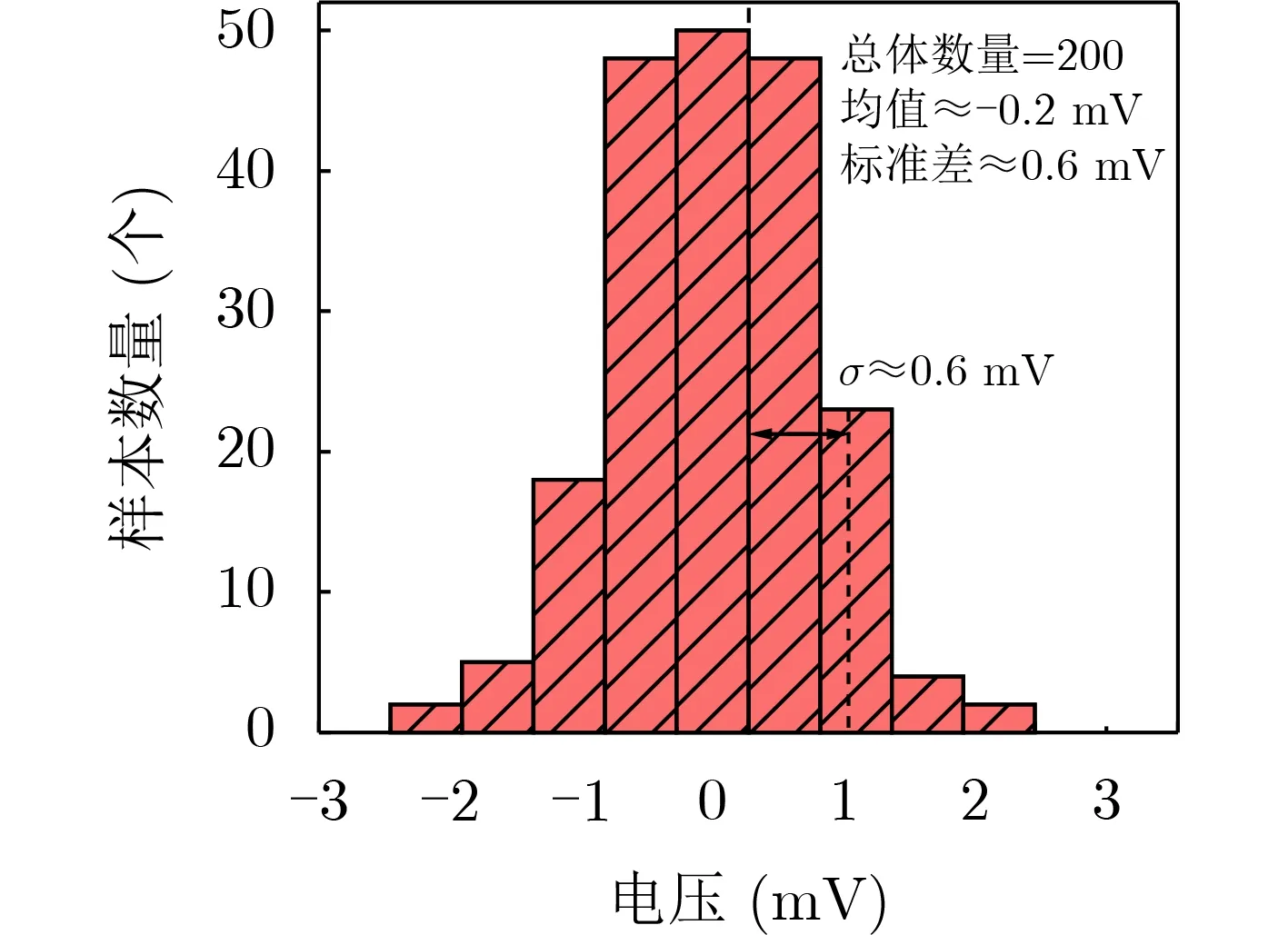
图13 蒙特卡罗失调分析

以上为绝对值电路子模块及整体电路架构性能仿真分析，为了实现绝对值电路在CIM架构中的运算功能，且最终能够拟合成Tanh激活函数，将ADC二进制输出值通过数字组合逻辑转化为Tanh激活函数，其仿真图如图14所示。其中蓝色曲线为理想Tanh激活函数曲线图，红色三角形离散点为通过CIM架构中ADC输出值经过数字逻辑转化后的曲线图。对两条曲线进行计算，拟合后的Tanh激活函数的平均误差为0.011。

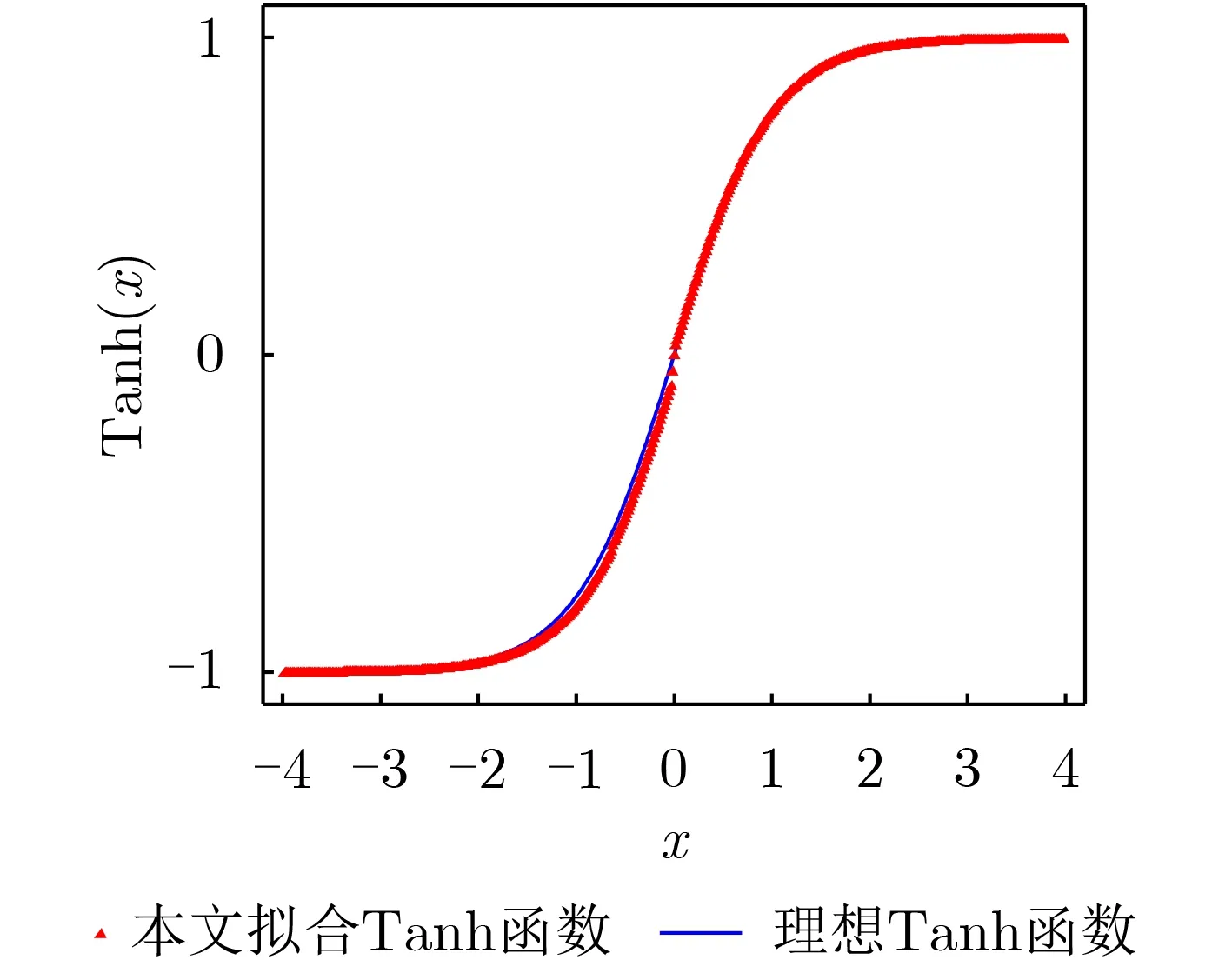
图14 理想Tanh函数与该文CIM架构输出值拟合成Tanh函数对比

表2展示了该绝对值电路与其他绝对值电路的对比分析。可以看出，该电路速度小于50 ns，高于其他电路；理论绝对值输出值与实际绝对值输出值之间相对误差小于1%；其面积以及低压适用条件等指标均处于中上水平。

表2 绝对值电路性能总结以及与其他绝对值电路性能对比

4.3 整体电路版图

本文设计的新型离散型、高速、高精度无二极管绝对值电路电源电压为1.2 V和–1.2 V。针对设计完成的绝对值电路进行相应的版图绘制，并根据以下要求对电路架构进行版图的布局及设计：

(1)为了降低温度变化对内部电路的影响，采用深阱工艺电阻，匹配基准电流源MOS管温度系数及反相比例取反电路正负端电压温漂。

(2)运放、基准电流源及比较器中电流镜负载及输入对管采用交叉匹配方式，并在两端增加虚拟(Dummy)管，提高MOS管对称性及匹配性，使之均匀传输对称支路电流。

(3)整体CIM架构集成在Flash型存算器件阵列中，由于存算器件尺寸较小，考虑到版图匹配等问题，不适合1对1(1条BL对应1条读出系统)的版图布局，根据器件宽度与读出系统宽度进行阵列式布局布线，并将读出电路系统进行堆叠设计，并考虑其布线通道等问题。

电路版图如图15所示。整体版图面积为4 447 μm2，在标准PVT条件下，取得仿真周期下流经电源电压的平均电流值，求得平均功耗为670 μW。适合低面积开销、低功耗存算一体架构及其他运算电路借鉴和考量。

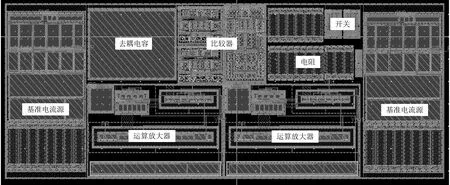
图15 绝对值电路整体版图

5 结论

为了解决存算一体模拟架构中Tanh激活函数负值难处理的问题，本文采用55 nm CMOS工艺创新设计出一种离散型无二极管绝对值电路，电路实现了正负压的高速、高精度转化输出，在不同PVT的工艺环境下对绝对值电路中各个子模块以及整体电路进行功能以及性能仿真和分析，均达到了设计需求。在输入电压为–100～100 mV，比较器的工作周期为50 ns，电源电压为1.2 V和–1.2 V条件下，绝对值电路在工作周期内均能够很好地输出相应的转化值，且输入输出的电压误差控制在1 mV以内，零点放大区域电压小于400 μV，整体电路功耗为630 μW，电路面积为4 447 μm2，实现了绝对值电路转化小面积、低功耗的要求，满足存算一体读出架构高算力、高精度的运算特性。因此，本文对低电源电压、低功耗、离散型正负压绝对值处理提供了有益的参考。