极化敏感阵列到达方向估计方法的FPGA实现

刘鲁涛 曹 莹* 郑 昱

①(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

②(南京电子技术研究所 南京 210039)

1 引言

波达方向(Direction Of Arrival, DOA)估计是战术和战略应用中许多电子战的主要组成部分，近代以来，由于军事和民用的迫切需求，DOA估计发展十分迅速[1–4]。多重信号分类(MUltiple SIgnal Classification, MUSIC)算法[5]作为经典的DOA估计算法，具有精度高、分辨力高和普遍的阵列适用性等优点。将普通阵元用极化敏感阵元代替之后，并按照特定的顺序在空间中排列的阵列系统称为极化敏感阵列[6]。和普通阵列相比，极化敏感阵列具有更高的抗干扰能力、抗角模糊能力、信号检测能力等优点[7]。因此，对基于极化敏感阵列的MUSIC算法的硬件实现的研究具有重要意义。

目前，DOA估计多采用数字信号处理器(Digital Signal Processor, DSP)多核运算实现，但DSP为串行操作，使得基于MUSIC算法的DOA估计局限在毫秒级，无法满足DOA估计的实时性。随着FPGA(Field Programmable Gate Array)技术的迅速发展，FPGA芯片的容量越来越大，提供的知识产权(Intellectual Property, IP)库也越来越全面，FPGA并行度高的优势逐渐展露，为提高DOA估计的实时性提供了更好的硬件选择。文献[8]提出了天线阵列缩减和协方差归一化技术，在100 MHz的工作频率下仅耗时2 μs即可完成DOA估计，但其提出的技术仅适用于常规的标量阵，并不适用于极化敏感阵列，且其使用代数计算的特征分解方法仅适用于协方差矩阵维数小于5的情况，有其局限性。文献[9]实现MUSIC算法的2维搜索，使用了雅各比(Jacobi)算法的串行脉动阵列结构以及多尺度峰值所搜方法，在100 MHz的工作频率下完成1次DOA估计需要1 ms。文献[10]提出了一种完全实数计算的MUSIC算法，为了缩减并行Jacobi算法的资源消耗问题，提出了一种新的脉动阵列结构，但同时为DOA估计的实时性带来了障碍，硬件耗时在毫秒级。文献[11]针对特征分解的繁重计算负荷以及耗时的问题，对Jacobi算法进行了优化，提出了一种并行Jacobi算法的一次旋转加速方法，但其硬件耗时仍然在几百微秒以上。文献[12]研究了几种矩阵分解算法在FPGA实现时对DOA估计性能的影响，其几种方法的硬件耗时均在微秒级，但没有考虑完整的MUSIC算法的实现。到目前对MUSIC算法的FPGA实现的研究均是基于传统标量阵列，对于基于极化敏感阵列的MUSIC算法的FPGA实现的研究仍需探索。对DOA估计的实时性的提高的研究也具有工程应用价值。

为了提高硬件效率和算法的实时性，本文提出一种实数化预处理方法，在此基础上提出一种基于极化敏感阵列的2维MUSIC算法的FPGA高效硬件实现方案。从阵列的特点出发，充分分析阵列的导向矢量，根据分布式极化敏感阵列的中心对称结构，得到导向矢量实部和虚部的对应关系。根据该对应关系构建线性变换矩阵，对接收数据做线性变换，使得极化MUSIC算法的计算得到了简化。FPGA实现方案主要包含实数化预处理、协方差矩阵计算、特征值分解、确定噪声子空间、谱峰搜索几个模块。并根据各模块独立计算的特点设计了流水线工作模式，充分发挥了FPGA并行计算的特点，完成了算法的低延迟和资源高效的FPGA实现。

2 基于极化敏感阵列的MUSIC算法

如图1所示的阵列为分布式极化敏感阵列，即天线阵列各阵元由1维分量构成，且具有不同的极化方式和指向，可无损耗接收对应极化方式的来波信号。

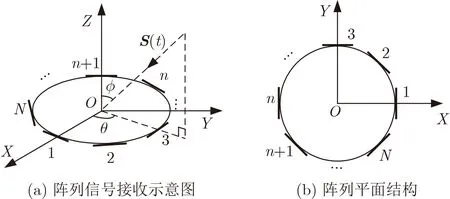
图1 分布式极化敏感阵列示意图

考虑由N(N=2K或N=2K+1)个阵元组成的一个分布式极化敏感阵列和M个远场窄带完全极化信号，第m个信号的方位角和俯仰角分别为θm和ϕm， 极化辅助角和极化相位角分别为γm和ηm。假设入射信号互不相关且与噪声之间相互独立，则该极化敏感阵列的接收信号可以表示为

式(1)中aθm,ϕm,γm,ηm为第m个入射信号的导向矢量，任一入射信号的导向矢量具有如式(2)的形式

其中，B=[B1,B2,...,BN]T为极化敏感矩阵，对于不同的极化敏感阵列结构和极化方式，B矩阵具有不同的形式，对于分布式极化敏感阵列，假设第n个阵元的指向角为αn， 则Bn=[cosαnsinαn]T,n=1,2,...,N。对于第n个阵元空域导向矢量un(θ,ϕ)具有如式(3)的形式

其中，f为信号频率，τn为不同阵元间的空间延迟，对于平面阵而言，若以原点为参考点，其具体形式为

其中， c=3×108m/s 为光速，(xn,yn)为第n个阵元相对原点的平面坐标。

接收信号的协方差矩阵为

由于信号和噪声是相互独立的，信号的协方差矩阵可以分解为信号子空间和噪声子空间两部分，其中RS是信号的协方差矩阵，ARSAH是信号部分。对协方差矩阵进行特征分解有

其中，US是 由R的M个较大特征值对应的特征向量组成的空间，称为信号子空间，UN是由R的N－M个较小特征值对应的特征向量组成的空间，称为噪声子空间[13]。

根据传统MUSIC算法可知，信号子空间US与噪声子空间UN是正交的，即信号子空间的导向矢量也与噪声子空间正交，那么可以构造空间-极化域谱函数为

式(7)有4个未知变量，那么就需要进行一个4维的谱峰搜索才能得到信源的DOA参数估计，这种搜索有非常多的搜索节点，在硬件实现时会造成较高的时间消耗。如果要减少谱峰搜索的搜索时间，那么就需要对极化MUSIC算法谱函数进行降维。

根据式(2)，式(7)可以进一步表示为

其中，hγm,ηm称 为极化矢量且满秩，是与DOA参数无关的向量，由式(9)表示

因此，极化MUSIC算法的空间谱函数可以表示为

此过程称为极化MUSIC算法谱函数的降维[14]。

3 极化MUSIC算法的FPGA实现

采用如图1所示的均匀分布的具有中心对称结构的分布式极化敏感阵列，在赛灵思(Xilinx)公司的Virtex7-690T FPGA芯片上，使用Verilog或System Verilog语言，在Vivado平台上进行综合仿真实现。

3.1 实数化预处理

将省略极化矢量的导向矢量展开为如式(11)的形式

根据阵元的中心对称关系，当N为偶数时，DH的第1个和第K+1个元素分别为

即DH(1)与DH(K+1)的 实部相反，虚部相同，且DV(1)与DV(K+1)也存在同样的对称关系，对于其他阵元也有同样的对称关系。当N为奇数时，阵列中心对称的阵元同样满足上述对称关系。

因此构造线性变换矩阵U

其中，IK为K阶单位阵，O为K维元素均为0的列向量。对接收信号X(t)做线性变换

此时，Y(t)仍然是复数数据，但数据的实部已经包含了相位信息，另外，硬件实现时实部和虚部作为IQ数据流分别输入到系统中，因此，下面本文以Y(t)的实部为例。图2显示了当N为偶数时实数化处理的FPGA实现示意图。对距离为K的所有元素对，实部相减，虚部相加，将复数数据转换为实数数据。

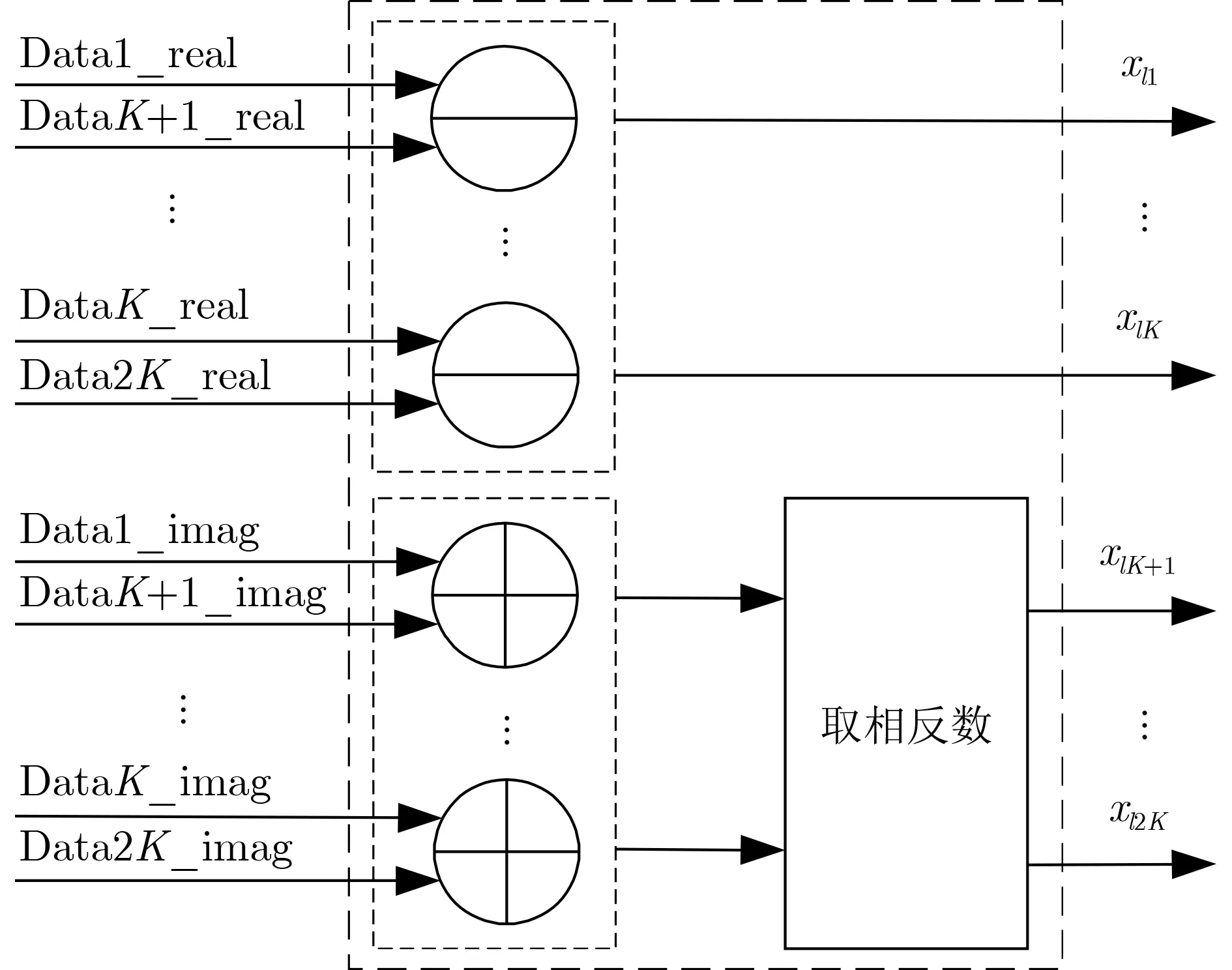
图2 实数化处理实现示意图

而此时导向矢量变为

至此，极化MSUIC算法的后续计算可以完全通过实数完成，相比于复数计算可以节约大量的硬件资源，同时缩短了计算时间，为DOA估计的实时性带来了可能。

3.2 协方差矩阵的计算

信号协方差矩阵R的计算公式为

其中，X为阵列接收信号，L为快拍数。由于在经过实数化预处理后R为实对称矩阵，因此只需计算矩阵R的上三角元素的值。此外由于取平均运算对后续计算没有影响，因此计算时可以省略快拍数L。综上可以将协方差矩阵计算式表示成如式(18)的形式

其中，xl(l=1,2,...,L)为阵列单快拍接收数据经过实数化预处理得到的数据。xlxlT形如式(19)

其中，xln(l=1,2,...,L,n=1,2,...,N)为xl的第n个元素。矩阵共有 ( 1+N)×N/2个上三角元素，每个元素通过定点数乘法器(Multiplier IP核)及定点数加法累加器(Accumulator IP核)并行计算，即可得到最终结果。

3.3 特征值分解

在得到协方差矩阵后，进行相应的特征值分解，从而得到特征值和特征向量。Jacobi算法是常用的特征值分解算法之一，主要通过对矩阵做一系列的旋转变换，将其变换成对角矩阵，从而计算出矩阵的特征值和特征向量[15]。本文选用并行Jacobi算法，充分利用FPGA和Jacobi算法的并行计算优势。使用Brent等人[16]提出的脉动阵列结构，将N×N维协方差矩阵的上三角元素拆分为N-1组，每组为N/2个 2 ×2的矩阵处理单元，根据每个单元在协方差矩阵中所处的位置可以分为对角单元和非对角单元，通过并行分组及调度规则保证同组N/2个处理单元之间独立并行地进行Jacobi旋转。当阵元数N=10时，并行Jacobi分组如表1所示。

表1 10×10矩阵的并行Jacobi分组

首先通过对角单元根据ϑ=1/2arc tan(2b/(a-c))计算旋转角ϑ的值，并根据式(20)对对角单元进行Jacobi旋转运算

同时根据式(21)对非对角单元进行Jacobi旋转运算

每组Jacobi旋转的FPGA实现结构如图3所示。通过调用CORDIC IP核的arc tan模式计算反正切值，

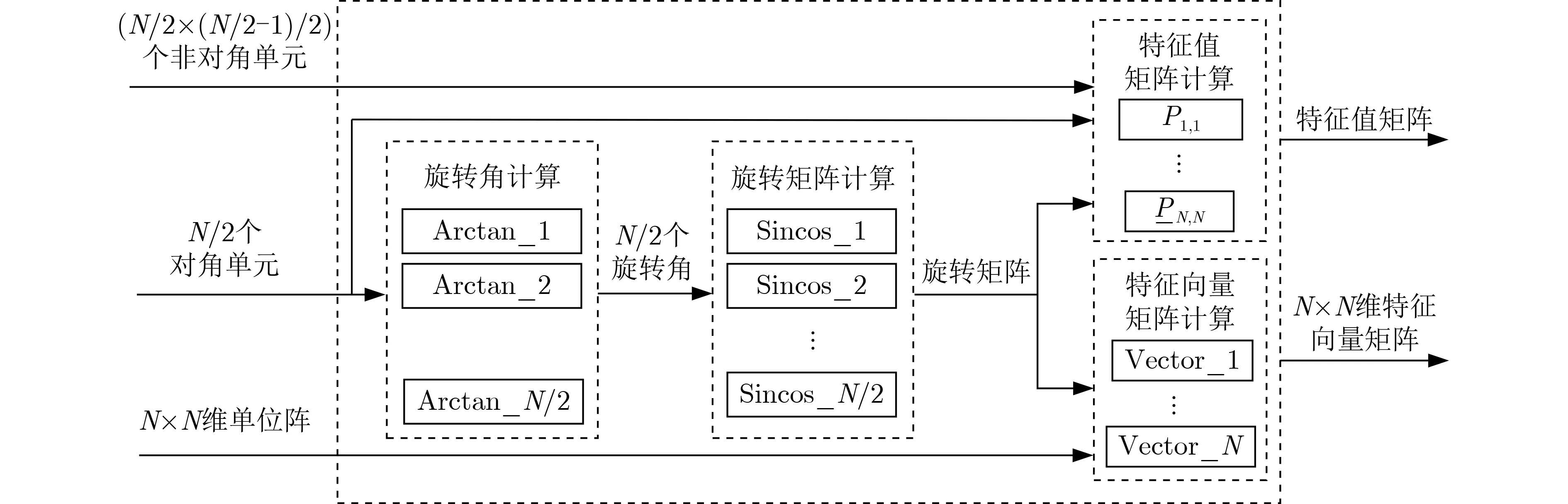
图3 单组Jacobi旋转实现示意图

从而求得旋转角ϑ，通过调用CORDIC IP核的sin and cos模式计算旋转角的正弦值和余弦值。完成一组Jacobi旋转之后，需要根据Jacobi分组进行数据交换，然后重复进行运算，直到完成N－1组Jacobi旋转，即完成1级清扫。由于每一组进行相同的迭代计算，为了节约资源，循环使用一组硬件资源N－1次来完成清扫，因此需要在输入端和输出端进行数据交换。同样为了节约资源，数据交换不采用矩阵乘法，而采用状态机直接进行寄存器赋值操作。

在进行特征值分解时，可根据实际需要进行多级清扫，清扫的次数越多特征值矩阵越接近对角阵，即误差越小，但同时会带来时间消耗的问题，可根据实际需求选择清扫级数。本文采用如图4所示的3级清扫结构，3级清扫的实现硬件结构相同，为节省FPGA资源，3级清扫重复使用同样的硬件资源。

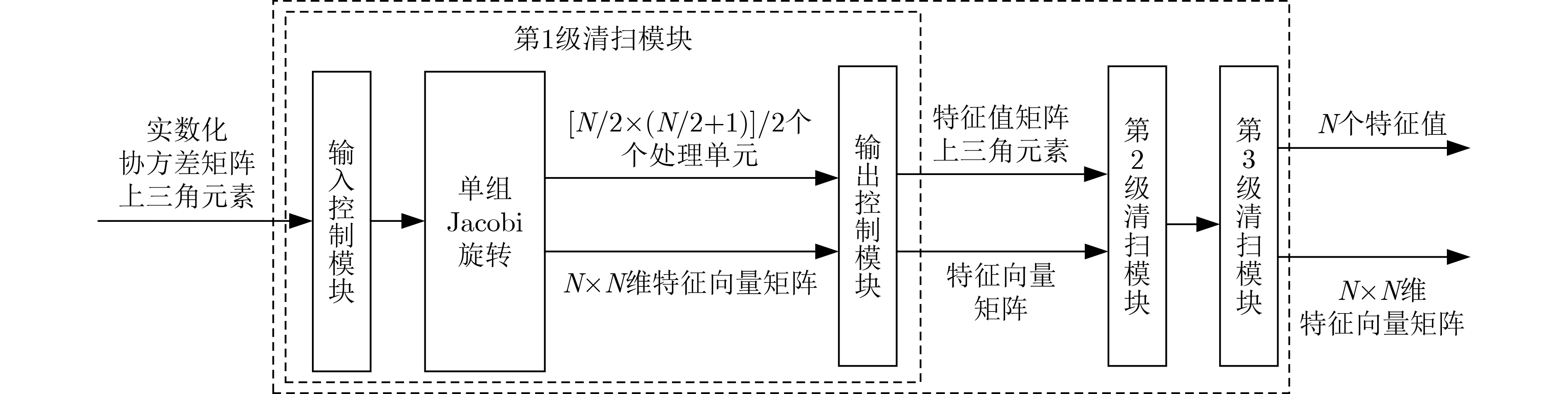
图4 特征分解实现示意图

3.4 确定噪声子空间

该模块首先对特征值进行排序，然后根据排序结果确定噪声子空间。对N个特征值进行从大到小排序，每个特征值均依次与N个特征值进行大小比较，计大于等于此特征值的个数即此特征值的排序结果。根据特征值排序结果，将对应的特征向量构成噪声子空间。由于特征值的物理意义为信号或噪声的功率，故特征值一定为正数，故通过运算符“<”和“==”进行特征值的比较。如图5为特征值排序的FPGA实现示意图。

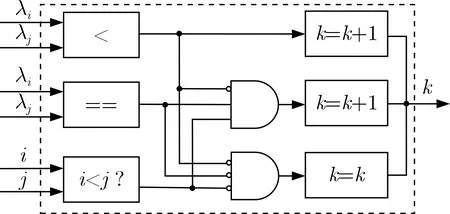
图5 特征值排序FPGA实现示意图

3.5 2维谱峰搜索

3.5.1 导向矢量计算

实数化之后的2维阵列的导向矢量形式为

其中， (θ,ϕ)为搜索角度，根据搜索范围及步进将其正弦值和余弦值保存到ROM中，导向矢量计算实现示意图如图6所示。

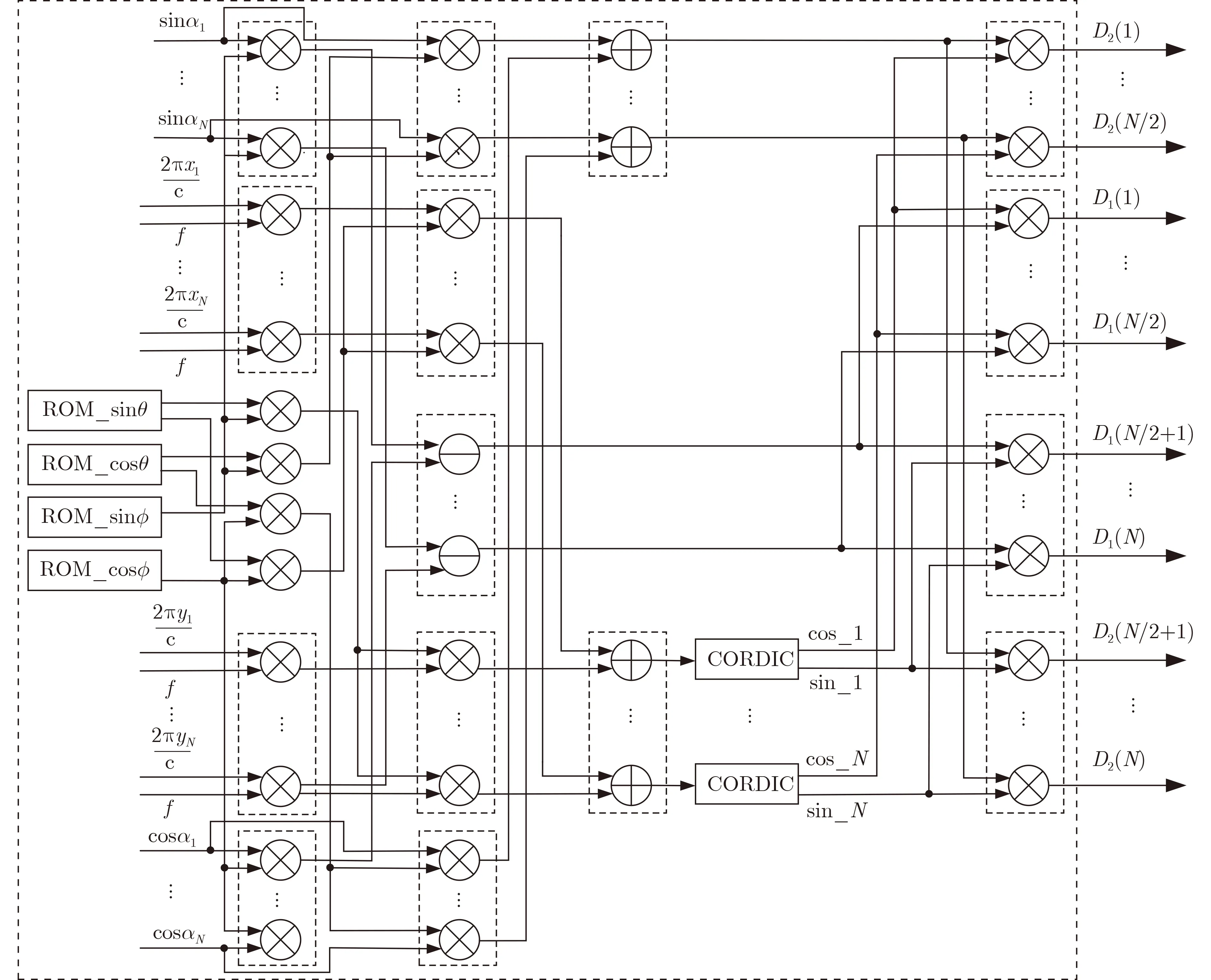
图6 导向矢量计算示意图

3.5.2 空间谱函数计算

由以上分析可知，经过降维和实数化处理之后的极化MUSIC算法的空间谱函数可以表示为

其中，U～N为实数化预处理得到的实数噪声子空间。为了简化计算，构造伪谱函数

计算空间谱函数值，首先以噪声子空间的第i列为例计算(θ,ϕ)×N(i)×(i)×Dr(θ,ϕ)，称为一个内部单元，其FPGA实现结构如图7所示。经过实数化处理后，噪声子空间为N×(N-M)维矩阵，即需要N-M个内部单元。如图8为空间谱函数计算示意图。

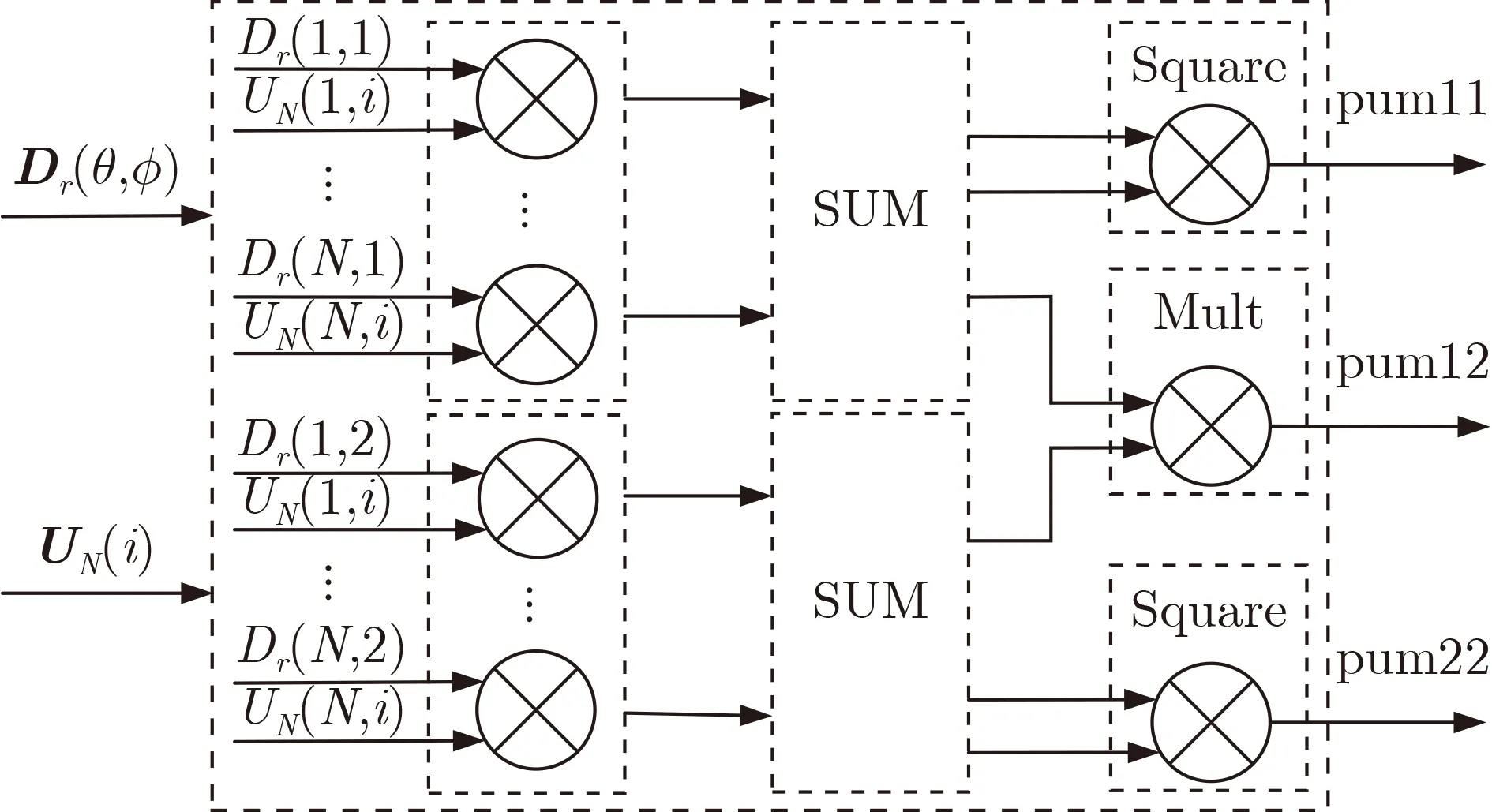
图7 内部单元计算实现示意

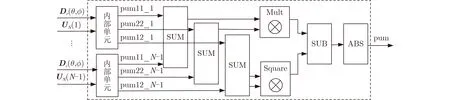
图8 空间谱函数计算实现示意图

3.5.3 谱峰搜索

当俯仰角和方位角的搜索范围分别为Rθ和Rϕ，搜索步进分别为 ∆θ和∆ϕ时，令I=Rθ/∆θ，J=Rϕ/∆ϕ。 这样(θ,ϕ) 能够划分为I×J的新矩阵，就可以将谱函数P(θ,ϕ)表 示为I×J的矩阵P

这样2维极化MUSIC算法的谱峰搜索问题就可以转化为从式(25)表示的2维矩阵的I×J个谱值中搜索局部极小值的问题。

Pi,jP(θi,ϕj)(i=1,2,...,I,j=1,2,...,J)

若用 表示 ，则需要满足Pi,j同时小于Pi-1,j-1,Pi-1,j,Pi-1,j+1,Pi,j-1,Pi,j+1,Pi+1,j-1,Pi+1,j,Pi+1,j+1，Pi,j才为一个极小值点，其空间位置谱谷值示意图如图9所示。搜索到所有谱谷值位置，然后将其依次按从小到大排序，得到最小的M个谱谷值相对应的俯仰角和方位角就是信号DOA参数的估计值。

图9 空间谱谷值示意图

从表达式可以看出，先将方位角θ固定不变，然后遍历俯仰角ϕ， 再将θ值进行改变，这样持续计算，就能够完成整个空域的搜索。在FPGA实现时通过FIFO IP核进行数据传输，以实现图10所示的九宫格数据比较结构。

图10 数据流水线处理框图

为了进一步减少计算量，采用两级搜索方式。首先进行搜索步进较大的粗搜索，在整个搜索范围内得到搜索结果 (,)(m=1,2,...,M)。再将搜索结果串行输入到第2级，在粗搜索的结果适当范围内以较小的搜索步进进行细搜索，得到最终估计结果(θm,ϕm)(m=1,2,...,M)。

3.6 流水线设计

由于谱峰搜索模块的耗时大于协方差矩阵计算、特征值分解和确定噪声子空间模块的总耗时，且各个模块的计算是独立的，故采用如图10所示的流水线处理结构，可以进一步提高DOA估计实时性，但谱峰搜索模块处理的数据为其他模块上一次工作的输出，故单次DOA估计时间为谱峰搜索模块的耗时。

4 实验结果与评估

4.1 FPGA资源占用

综合考虑硬件资源、时间资源以及算法精度之间的平衡，使用定点数实现算法，虽然数据精度会有一定的牺牲，但在硬件资源、时间资源方面却可以成倍的节省。

受FPGA资源的限制，传统极化MUSIC算法使用8个阵元的分布式极化敏感阵列，而实数化的MUSIC算法使用10个阵元的阵列，当快拍数为100，搜索范围为θ∈[0,360◦],ϕ∈[0,30◦]，粗搜索和细搜索的步进分别为2°和0.2°，当芯片的工作频率为100 MHz时，消耗的硬件资源情况如表2所示、消耗的时间如表3所示。

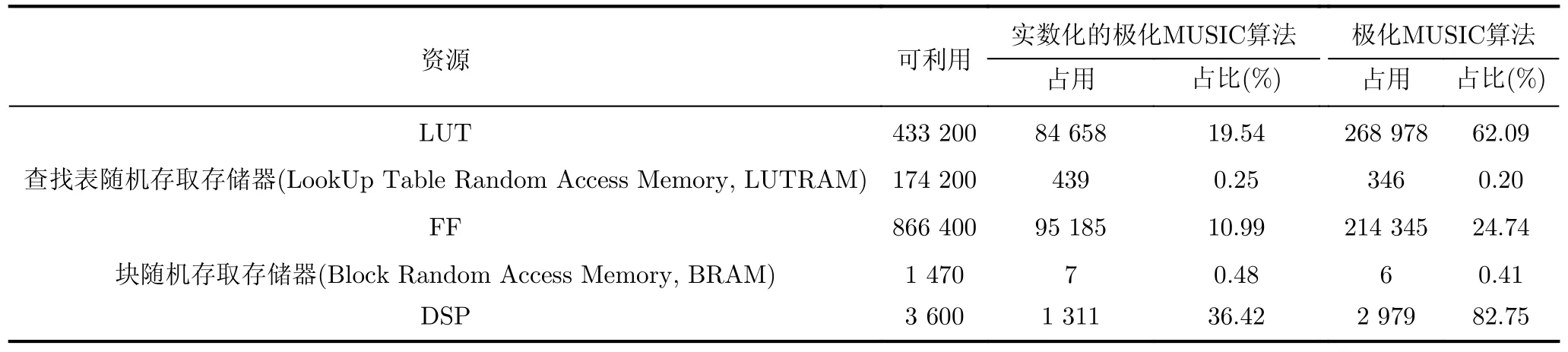
表2 资源占用情况

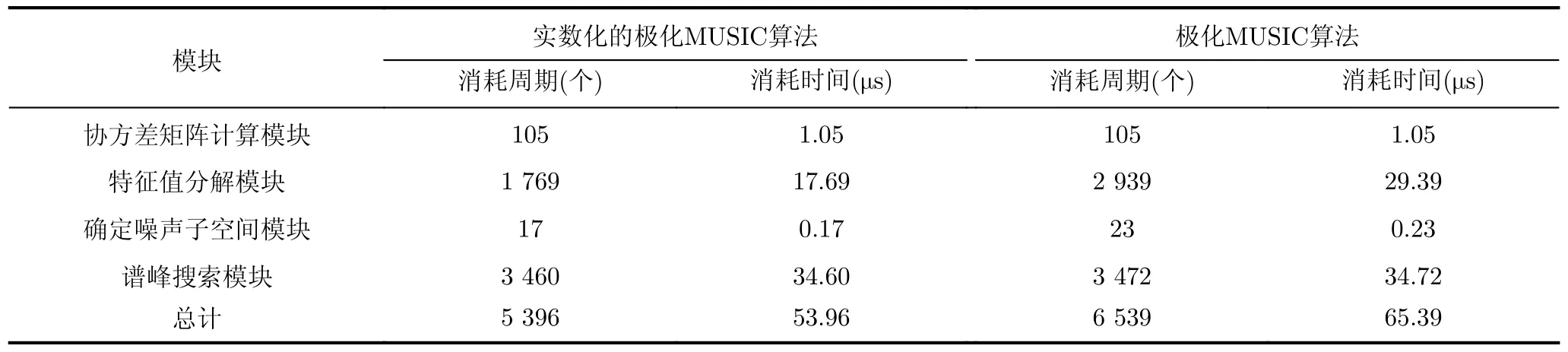
表3 各模块消耗时间

由表2可以看出，对于查找表(LookUp Table,LUT)、触发器(Flip-Flop, FF)和DSP资源，提出的实数化的极化MUSIC算法的利用率远远低于传统的极化MUSIC算法，这表明提出的方案计算量显著减少。此外，从表3可以看出，就时间消耗而言，这两种算法在特征值分解模块中的差异最大，主要是因为传统极化MUSIC算法的复数计算使特征值分解中的协方差矩阵的维数加倍，而该方案通过实数化预处理避免了这一问题。由于流水线设计，提出的实数化的极化MUSIC算法需要34.60 μs即可输出一次DOA估计参数。注意，与传统的极化MUSIC算法相比，所提出的方案利用了更多的阵元，与基于10阵元阵列的极化MUSIC算法相比，资源占用和时间消耗的改进将进一步提高。

4.2 算法的DOA估计结果及性能评估

设置两个信源，DOA参数分别为(77.6◦,11.6◦)和(277.2◦,26.1◦)，极化参数均为(γ,η)=(45◦,15◦)，如图11为DOA参数估计结果图。由图可知，实数化的极化MUSIC算法的谱峰要比极化MUSIC算法的谱峰低，但仍然有明显的谱峰。

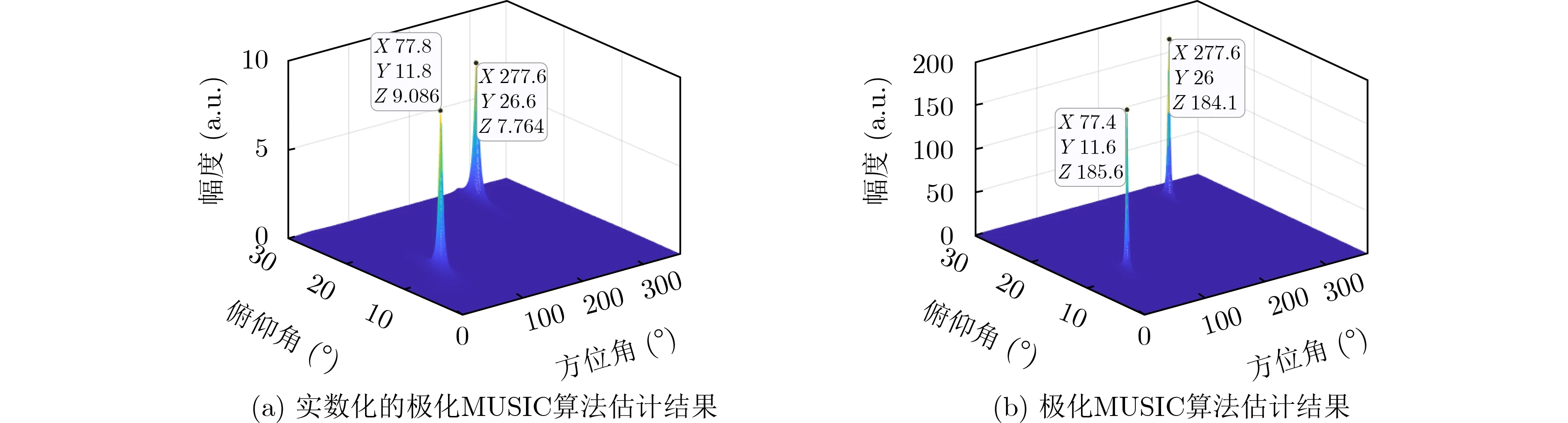
图11 DOA参数估计结果

假设单信源入射到该阵列，信源DOA参数在搜索范围内随机给出，极化参数为(γ,η)=(45◦,15◦)，接收信号信噪比为0～28 dB，快拍数为100，搜索步进为0.2°时，使用极化MUSIC算法、通过线性变换实数化的极化MUSIC算法以及对接收数据线性变换后分别取实部和虚部的极化MUSIC算法，各做1 000次Monte-Carlo实验，得到均方根误差(Root Mean Square Error, RMSE)随信噪比变化的曲线如图12所示。其中RMSE的计算式为

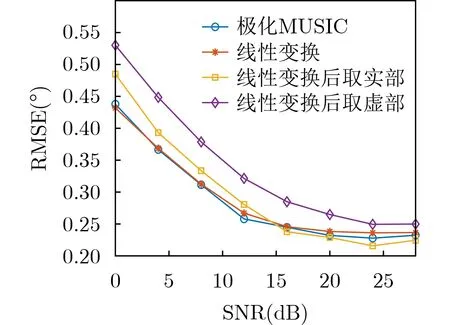
图12 均方根误差随信噪比变化曲线

其中，C为Monte-Carlo实验中测向结果正确的次数，θc,ϕc为第c次实验的真实DOA参数，,为第c次实验的DOA参数估计值。由图12可知，线性变换后的极化MUSIC算法与极化MUSIC算法的性能几乎一致，取实部和虚部后性能略有所降低，但随着信噪比的提高，取实部后的性能有所提高。相比于实数化节省的计算量，其性能的降低可以忽略，由此得出实数化的极化MUSIC算法具有重要的工程应用价值。

5 结论

本文首次研究了极化MUSIC算法在FPGA上的实现。为了解决传统复数极化MUSIC中的资源占用和时间消耗问题，提出了一种实数化预处理方法，利用均匀圆阵的中心对称结构，通过线性变换将接收数据和导向矢量转换为实数。通过实数运算，协方差矩阵计算和特征值分解的时间消耗显著减少。此外，本文还构建了所提出的实数化的极化MUSIC算法在FPGA上的整体实现方案，详细说明了各模块的设计。为了有效地连接所有模块，本文还设计了一种流水线实现结构。根据实验结果，在100 MHz的工作频率下，完成一次完整的DOA估计需要53.96 μs，同时保证了估计精度。该实现方案具有精度高、实时性好、资源消耗低等优点，具有较大的工程应用价值。