脉冲神经网络权重量化方法与对抗鲁棒性分析

李 莹 李艳杰② 崔小欣 倪庆龙② 周崟灏*

①(中国科学院微电子研究所 北京 100029)

②(中国科学院大学集成电路学院 北京 100049)

③(北京大学集成电路学院 北京 100087)

1 引言

人工智能正成为推动人类进入智能时代的决定性力量[1]，在自动驾驶、医疗救助、政府管理等安全攸关应用中，人工神经网络(Artificial Neural Networks, ANN)面临着以对抗攻击为代表的各种攻击威胁。对抗攻击来源于人脑与机器智能的识别差异，可定义为通过对输入注入人类难于辨识的扰动来欺骗神经网络模型，使其达到高概率的错误输出。愚弄模型[2]、操纵语音助手[3]、错误过滤垃圾信息[4]等案例层出不穷，可能造成泄露关键数据，甚至决策错误[5]，严重影响系统应用的准确性、机密性和完整性。对抗攻击已经成为影响深度学习模型成功的最大挑战之一。

类脑芯片在结构上多采用脉冲化的神经网络(Spiking Neural Networks, SNN)，具有高稀疏性、低功耗等特点，已成为第3代神经网络的代表[6]，有望大规模地用于视觉分类等低延迟目标识别任务。SNN的固有结构使层间数据具备天然的稀疏性[7]，使其比ANN有显著的对抗鲁棒性提升。国内外相关研究主要聚焦在算法模型分析层面，Sharmin等人[8]提出了一个简单的对抗攻击框架，并指出通过泊松编码的输入离散化和泄漏-积累-发放(Leaky Integrate-and-Fire, LIF)神经元的非线性激活是SNN鲁棒性的来源。El-allami等人[7]研究了SNN对不同神经元放电电压阈值和时间窗边界值条件下的攻击鲁棒性。Kundu等人[9]从权重、泄漏、阈值和时间步长等方面评估了视觉几何组(Visual Geometry Group, VGG)网络结构的鲁棒性。Kim等人[10]在低延迟训练中比较了两种编码的鲁棒性、能量效率、准确性等特性。上述研究中均没有考虑算法到电路的映射，而类脑芯片在实际应用中，必然要通过重要参数的量化来配置电路单元，进而完成网络推理。

本文通过在对抗攻击前向推理的加载顺序之前加入感知量化函数，从而模拟量化压缩后的权重在推理过程中的精度损失，将感知量化框架与对抗攻击训练/推理过程相融合，能够对网络部署到硬件的量化过程中鲁棒性损失进行度量。主要贡献如下：

(1) 针对基于梯度攻击的对抗攻击算法，在不同网络拓扑上构建了适用于对抗攻击训练的基于替代梯度的SNN模型和对抗样本。

(2) 创新性地提出一种权重感知量化的方法，建立感知量化与对抗攻击训练/推理相融合的评估框架，在不同脉冲编码和网络参数组合条件下，通过引入攻击前后推理精度损失差、层间脉冲活动和脉冲信噪比等度量依据，解释量化稀疏性与对抗鲁棒性的联系。

(3) 基于类脑芯片模拟器完成部署和对抗推理，对SNN对抗鲁棒性实现了全栈评估。

具体结构安排如下：第2节介绍支持对抗鲁棒性分析的SNN算法与对抗样本生成，第3节介绍本文提出的权重量化方法和评估框架，第4节通过实验分析了量化前后不同对抗鲁棒性评估依据的差异，并在实际类脑芯片中进行了硬件验证，第5节总结全文。

2 支持对抗鲁棒性分析的SNN算法与攻击建模

2.1 基于反向传播和替代梯度的SNN算法

SNN训练常用到的算法有3种：(1)ANN转换SNN方法[11]；(2)基于反向传播和替代梯度的方法(Spatio-Temporal Back-Propagation, STBP)[12]；(3)无监督脉冲时间依赖可塑性 (Spike-Timing-Dependent Plasticity, STDP)及其变体方法[13]。由于转换SNN的算法需要较大的计算资源和调试优化时间，而STDP没有梯度反向传播的过程，且损失函数不可导，不易生成对抗样本，因此，使用STBP训练算法，将替代梯度算法与时间反向传播算法融合，解决了SNN层间脉冲反向传播不可导的问题。反向传播主要利用链式求导法则计算损失函数相对于网络参数的梯度。导数的链式法则是微积分的基本规则，允许通过应用其组成函数的导数来计算复合函数的导数。SNN时空展开的链式求导结果如式(1)

L表loss函数，O代表神经元输出，U代表神经元电压，t代表当前的第t个单位时间，l代表网络的第l层，W代表对应节点上的权重。

由于SNN中隐藏层的LIF神经元只有在膜电位超过放电阈值时才产生脉冲输出，导致不可微。为了利用标准的基于反向传播的优化程序，本文使用了替代梯度技术。参考利用导数中峰值时间信息的梯度逼近函数进行替代梯度计算的方法[12]。线性函数替代梯度的数学公式如式(2)

ot和ut为时间步长t时的输出峰值和膜电位。θ为神经元阈值电压。

图1(a)为同一神经元在时间上展开后的链式求导法则原理，在一轮训练权重更新的过程中，对应每个单位时间T上的权重信息累计得到这一轮训练权重更新的最终数据。图1(b)为不同层神经元在时间上展开后的求导原理。

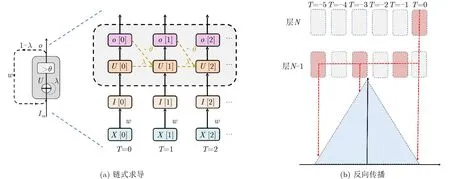
图1 链式求导法则在时间和空间上展开后的求导原理

2.2 对抗攻击建模

Szegedy等人[14]于 2013 年发表了第1篇深度神经网络的对抗性攻击论文，并创造了术语“对抗性示例”。随后Goodfellow等人[15]也提出了具有单个梯度步长的对抗性示例：快速梯度符号方法(Fast Gradient Sign Method, FGSM)。后续出现更多的对抗算法，如R + FGSM通过随机化步骤来增强攻击[16]，投影梯度下降(Projected Gradient Descent,PGD)则采取多个较小的步骤迭代对FGSM进行了改进[17]。SNN对抗攻击包括：(1)对抗样本的生成；(2)对抗样本的注入。首先将原始样本叠加上权重和扰动因子的乘积后生成新的样本，然后将样本重新注入网络进行训练，更改要攻击的标签后进行反向传播和梯度下降，训练多轮直到最终分类结果修改为攻击目标效果后，导致SNN做出不正确的预测。

SNN对抗攻击的建模首先需要确定一个数据集(x,ytrue)个 分类模型h，其中x为干净的图像，ytrue为正确标签，对抗攻击的概念是找到一个输入xadv，使得x和xadv无法区分开，但分类模型h错误地区分了xadv，即在错误标签上产生高概率输出。在本文中，主要考虑FGSM生成xadv的方法，如图2。其中的Loss为SNN替代梯度训练过程中前向传播后的损失函数，Grad为训练过程中反向传播后获得的梯度信息，Adv_Grad为保存中间梯度信息的节点，Adv_Loss为原始样本推理精度减去对抗样本推理精度的差值，Embedding Weight是指将训练最后一轮的权重信息重新加载到推理过程中。

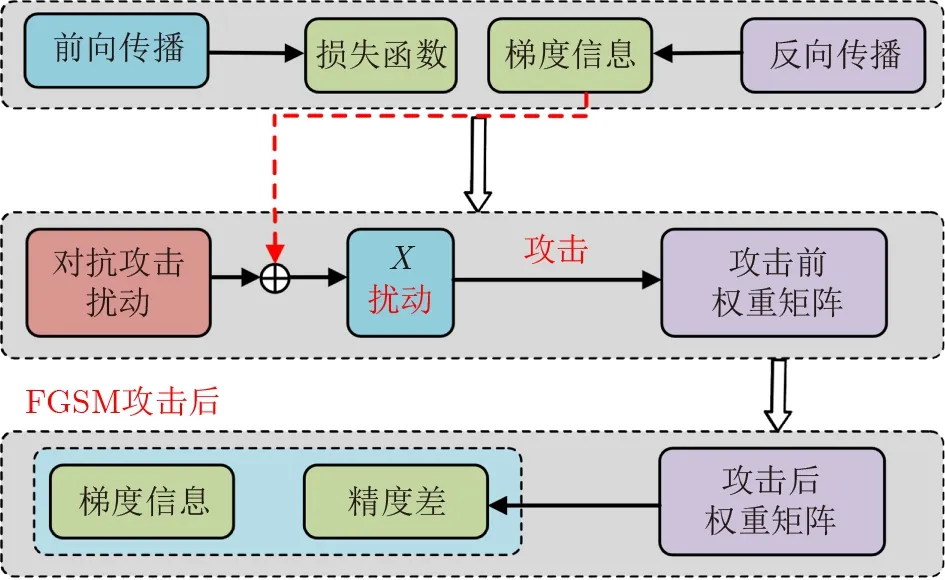
图2 FGSM攻击原理

2.2.1 FGSM攻击

FGSM是产生对抗性干扰的最基本和最广泛的方法，分为非目标和目标两种方式。

非目标FGSM如式(3)

FGSM如式(4)

这里ϵ指扰动量，通常ϵ远小于x，∇xJ是损失函数相对于原始干净数据的梯度。

2.2.2 对抗样本生成

假设X是32×32矩阵，卷积的核大小W是3×3。卷积是以1的填充和1的步幅执行。然后输出Y将保持32×32的大小(Y维度=X维度 + (2×padding)–W维度+ 1)。当Y=X⊛W时可以得到：。由于编码方式不同，X和Xencode的差异也不同，导致最终不同编码方式下求导得到的∂J/∂X也存在很大差异，这会影响到最终对抗攻击的效果，因此本文作了近似假设，如式(5)和式(6)

经过补丁操作以后的结果如式(7)

损失函数用J表示，J对X的梯度也是一个32 ×32的矩阵，每个元素用链式法则描述，并表示为矩阵的形式为式(8)。假设输入图像表示为X,W表示卷积层的权重矩阵，Y表示卷积运算的输出。合理进行以下近似假设如式(9)和式(10)

利用替代梯度技术通过网络反向传播损失而得到的。然后用式(9)求得对抗扰动，可以得到

W是Wconv1旋转180°。将式(11)的结果代入式(3)和式(4)中，即可得到FGSM攻击的对抗扰动值。如式(12)

具体攻击算法的迭代次数即可得到最终的对抗样本。由于对抗攻击过程只在前向推理过程中进行，但是对抗样本的生成过程，需要利用反向传播的权重数据。因此利用权重数据和FGSM算法生成的对抗样本注入网络来完成攻击。更多算法建模和分析可参考文献[18]。

3 权重量化方法与评估框架

3.1 量化稀疏

量化是将神经网络中的浮点数参数和激活值转换为低位整数或定点数的过程，通常会牺牲一定的模型精度以换取更小的模型尺寸和更低的计算量，从而使得神经网络可以在资源有限的场景中运行。深度神经网络模型中，通常权重由float32浮点数量化为int8, int4等定点数，减少模型的可表示空间大小。当 SNN 的权重被量化时，由于权重变得非常小，在某些情况下甚至为0。因此，连接到这些小或零值权重的神经元将接收到非常少的输入，从而造成网络输出的稀疏性。量化稀疏性有助于防止过度拟合训练数据。但过度的量化稀疏会导致大多数神经元沉默，影响网络推理精度和训练效果。因此，权重量化方法需要综合考虑量化比特选择、量化函数，以及量化和对抗框架的执行顺序等要素。

3.2 权重量化方法

在机器学习中，模型量化通常包括两种方式：后训练量化和感知量化。后训练量化是在模型训练完成后对模型参数进行量化，可将原本使用浮点数表示的参数转换为使用更少的比特位表示。感知量化是在模型训练期间对模型参数进行量化，可在不降低模型精度的情况下，显著降低模型参数的存储和计算开销。

为了使量化比特宽度范围更广泛，本文使用K-bit量化函数来调节量化的bit位宽。如式 (13)，[.]代表round操作，将输入张量的每个元素四舍五入到最近的整数

3.3 量化函数

根据2.1节的描述，SNN中每一层输出脉冲不可导，故而在训练过程中引入了替代梯度。量化的过程是在训练的每一轮中插入伪节点，在训练过程中对权重信息进行量化并存储到权重伪节点。在训练的前向传播中利用伪节点的权重信息进行推理，然后求得该轮的损失值loss后，进行反向传播并更新权重信息。在下一轮训练中重复这种执行顺序，直到达到适合的推理精度，并保存此时的权重信息。在定义SNN前向推理网络时，也要将感知量化函数插入到同样的地方，需加载训练过程最后一轮保存的权重信息，在推理时对该权重进行裁剪量化和存储，利用伪节点权重做前向推理即可得到真实的量化后的网络推理结果。

感知量化函数主要包括以下4个内容：

(1) 初始化网络：定义变量，定义网络节点用于索引网络中每一层参数，网络初始化；

(2) 构建参数张量节点(伪量化节点)：用于保存前向推理过程中量化参数；

(3) 裁剪函数：将浮点权重按层进行裁剪，利用式(17)完成裁剪，用于k-bit量化；

(4) restore函数：用于存储将反向过程中原始权重参数值还原到原始节点。

3.4 融合对抗攻击与量化的训练/推理框架

在具体模型的实现中，需要将对抗攻击与量化的训练和推理框架进行融合，算法1为加入了感知量化算法的训练框架，算法2为感知量化与对抗攻击融合的推理框架。

算法1 加入感知量化算法的训练框架

4 实验结果与分析

4.1 量化后的对抗鲁棒性分析

神经网络算法部署在类脑硬件上时都要进行权重裁剪，因此量化权重必然会引起推理过程的稀疏性变化，进而影响对抗鲁棒性。本节通过3.2节的方法对VGG5和VGG9进行了4 bit的权重量化，并使用对抗攻击融合的推理框架，分析对抗鲁棒性的差异。(1)VGG5推理精度损失和对抗鲁棒性差异。表1展示了VGG5在最优推理精度时(参数为(0.4,1.0,0.5))，量化前后不同攻击强度下的推理精度损失，损失越大表明对抗鲁棒性越差。Q1代表权重量化前，Q2代表权重量化后。量化前后推理精度损失差在可接受范围内。组合参数的3个数值分别代表conv层阈值电压，fc层阈值电压和泄露因子λ。I代表FGSM_2攻击，II代表FGSM_8攻击，III代表FGSM_16攻击。4种编码的对抗鲁棒性在量化后都大于量化前。直接编码的鲁棒性最差。为了更深入分析量化前后的对抗鲁棒性规律，在更深层的VGG9网络上针对更多组合参数进行了实验。(2)VGG9推理精度损失表2为在FGSM攻击下，不同组合方式在权重量化前后推理精度损失的对比变化幅度表征了不同参数下的结果波动范围。

表1 VGG5量化前后不同攻击强度下的推理精度损失(%)

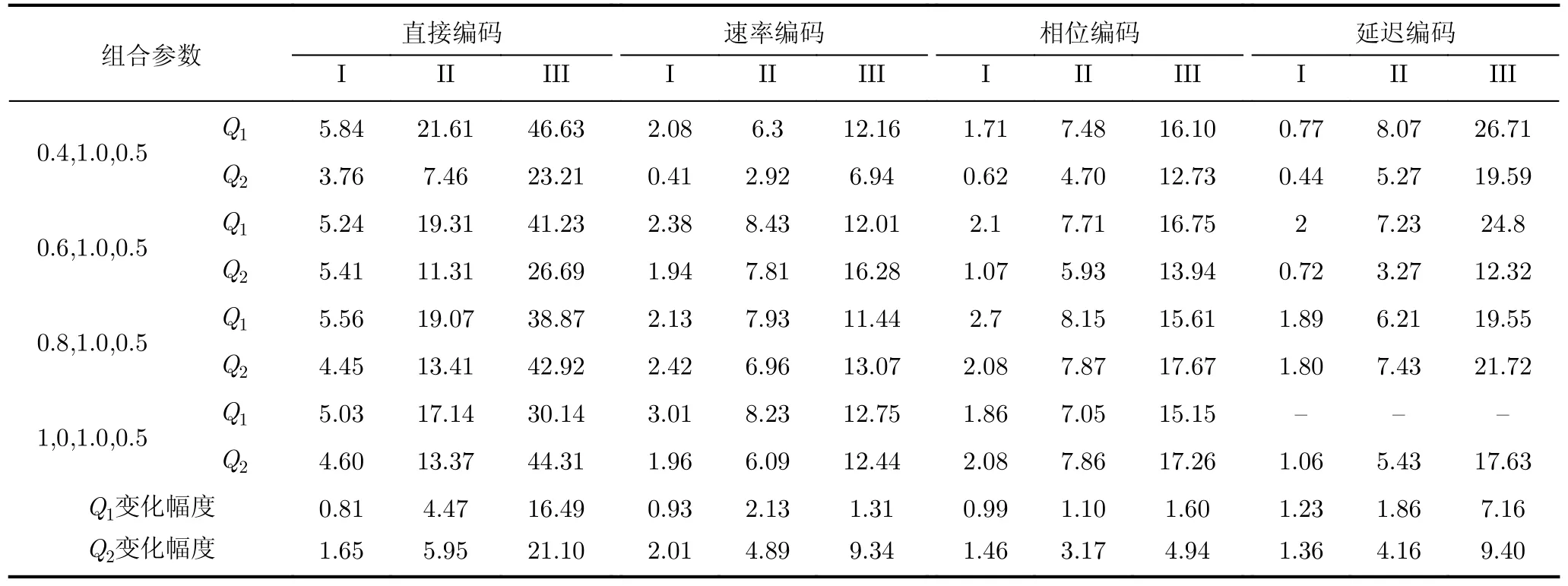
表2 VGG9量化前后不同攻击强度下的推理精度损失(%)

算法2 感知量化与对抗攻击融合的推理框架

由表2中结果可以看到：

现象1在相同(θ,λ)组合参数的情况下，无论哪种攻击强度，直接编码在4种编码方法中都显现出最差的鲁棒性。

现象2对于3种稀疏编码(速率编码、相位编码和延迟编码)在低阈值电压(θ=0.4)时，量化后对抗鲁棒都高于量化前的对抗鲁棒性。升高阈值电压(θ= 1,θ=0.6和θ=0.8)时，对抗鲁棒性分布无规律性。各种编码方式都在(θ=0.4)时表现出最好的鲁棒性，量化前只有局部最佳阈值点。

现象3量化后随着组合参数的变化，在低强度攻击下直接编码的adv_loss最大差异为1.65%，在高强度攻击下为21.21%。速率编码对低强度攻击最大差异为2.01%，对于高强度攻击为9.34%。相位编码对低强度攻击最大差异为1.46%，对于高强度攻击为4.94%。延迟编码对低强度攻击最大差异为1.36%，对于高强度攻击为9.4%。较于量化前对固有参数变化时的推理精度损失变化幅度均有所增大，均值为5.79%，涨幅为73.23%。

(1) VGG9层间脉冲活动。图3(a)—图3(d)分别代表了在没有对抗攻击的情况下，量化前后不同编码方式和参数下的脉冲活动，可以看到量化前后脉冲活动基本保持在同一数量级。

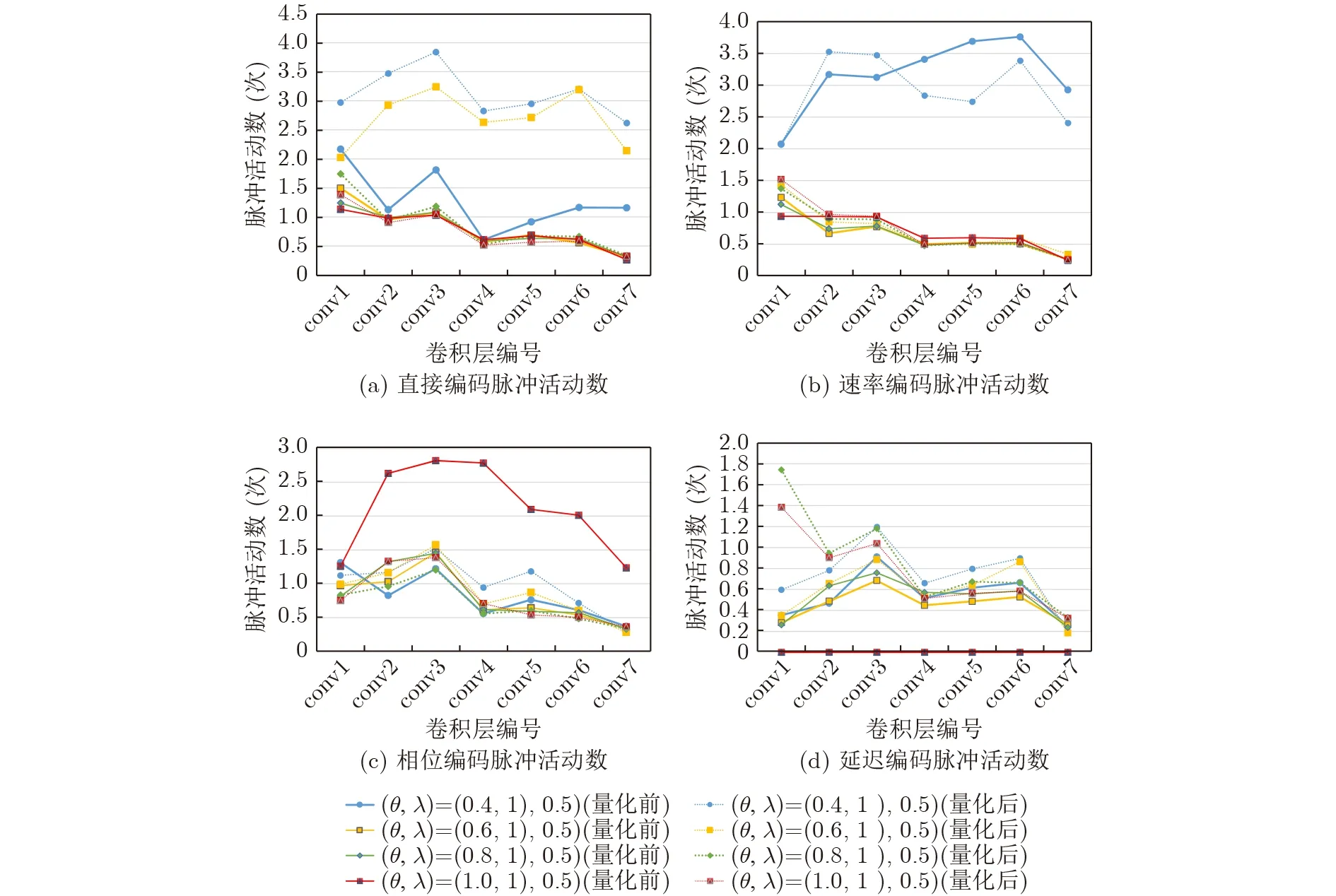
图3 量化前后不同组合方式下的脉冲活动

以FGSM-2攻击为例，表3为不同组合参数和编码方式在权重量化前后平均层间脉冲活动的差异(个别数值由于训练失败缺失)。可以看到，直接编码、相位编码和延迟编码结的层间脉冲活动均值的在量化前后变化幅度明显变大，平均涨幅为51.6%，而速率编码则稍有减少。

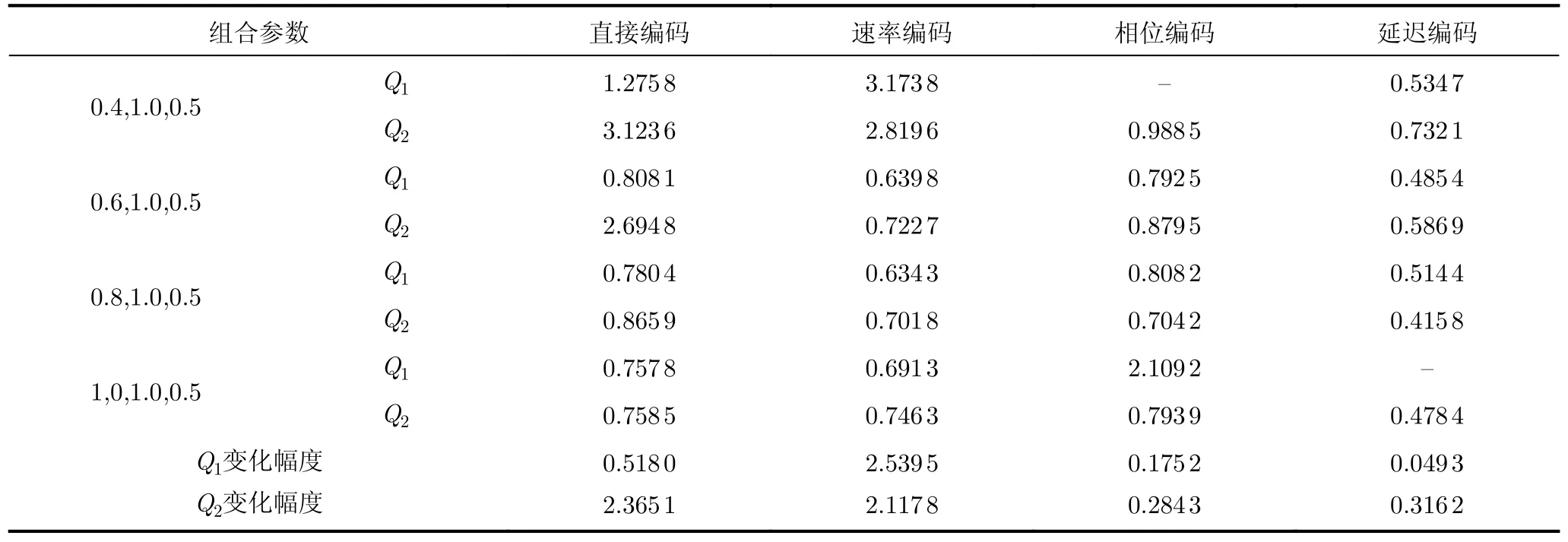
表3 量化前后不同攻击强度下的层间脉冲活动均值

(2)脉冲信噪比。对抗样本和原始样本会因攻击强度的不同存在不同的噪声强度。根据输入数据传递的时空特性，以及输入编码后数据积累用于脉冲发放的特性，将原始样本和对抗样本在推理过程中层间的原始样本脉冲活动数SA1与SA1-SA2的差值的比值定义为对抗样本与原始样本的脉冲信噪比(Signal to Noise Ratio, SNR)，其倒数为噪信比(Noise to Signal Ratio, NSR)，如式(14)

在分析中使用脉冲信噪比SNR(或NSR)，可以将影响层间脉冲稀疏性的因素包含在内，更好地反映加入干扰后网络是如何受影响而做出错误判断的，同时还考虑时间步T的影响。攻击强度ε/255代表对抗样本相对于原始样本在每个图像通道上被改变的幅度，一旦数据被编码送到每个神经元后，对抗样本的附加干扰就会被随机加到每个神经元上参与神经的积累电压与发放脉冲过程，从而影响最终的分类结果。

图4为加入对抗攻击后，量化后不同编码方式和组合参数作用下的NSR的结果。可以看到：

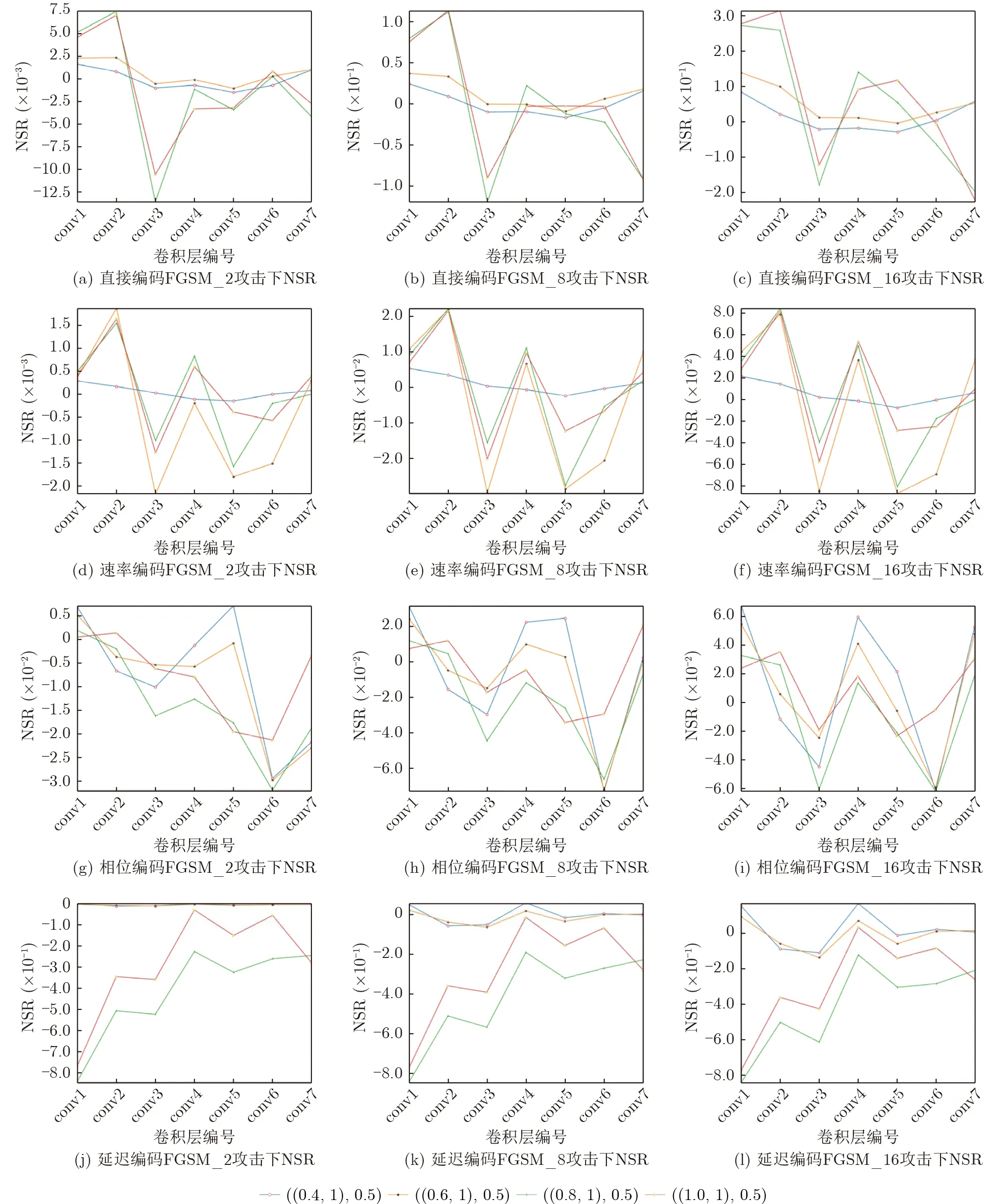
图4 量化后不同编码方式下的脉冲NSR

(1)在相同编码方式下，随着阈值变化，NSR的波动趋势一致。

(2)4种编码方式都存在NSR波动幅度相对最大的阈值点或波动幅度最小的阈值点，直接编码、速率编码和延迟编码都是θ=(0.4,1)NSR波动幅度都最小，延迟编码在θ=(0.8,1)和θ=(1,1)上NSR波动幅度更大，相位编码不同阈值下幅度相当。

(3)同一种组合参数，不同编码方式NSR的差别数量级不同，本文以1, 0.1, 0.01, 0.001和0.000 1为数量级的衡量依据来描述NSR的差异，结果如表4。无论在何种攻击强度下延迟编码NSR值都最大，这说明对抗样本和原始样本影响层间脉冲的发放程度更大。

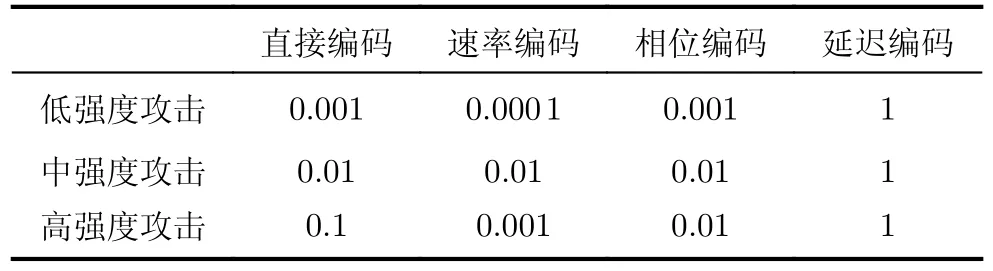
表4 NSR数量级差异

分析1在同一种编码方式下，对抗鲁棒性存在最佳阈值点，且最佳阈值点的NSR波动相对其他阈值点低。当调整单一参数时，总会存在一个极点使对抗鲁棒性达到相对最佳，而低于或者超过这个设定值时，就会出现鲁棒性的下降的趋势。且NSR越低对抗样本对层间脉冲改变量越小，此时鲁棒性越好。

分析2不同编码方式的Xclean影响了W的分布，中间存在替代梯度和权重量化两个近似过程，导致了W是模拟混淆值，所以编码越稀疏，模型越具有较高的鲁棒性。

由上述实验结果的综合分析可以得出如下结论：

(1)阈值增加，稀疏编码，权重量化都可以作为层间脉冲稀疏化的因素。其加剧稀疏化的趋势是，阈值增加大于权重量化bit降低大于稀疏编码。当稀疏因素单一时，对抗鲁棒性趋势是单调的，而当稀疏因素达到3种时，训练的模型有很大的脆弱性，导致对抗鲁棒性下降。

(2)单一的参数因素与对抗鲁棒性之间并不是线性关系。关于模型对抗鲁棒性的比较必须在固定系统模型参数的前提下。当调整单一参数时，总会存在一个极点使对抗鲁棒性达到相对最佳，而低于或者超过这个设定值时，就会出现鲁棒性的下降的趋势。

4.2 类脑芯片硬件验证

为了验证本文的权重量化方法与实际硬件上的兼容性，将提出的SNN框架在权重量化后部署到类脑芯片的硬件中。实验平台为北京大学PKUNC64C[19]类脑芯片，如图5。该芯片是一款多核脉冲神经网络类脑芯片，芯片采用2D Mesh NOC架构，集成了64k个随机LIF神经元和64M神经突触，可实现脉冲神经网络模型的高效推断功能。芯片配套设计工具链包括完整的芯片行为硬件模拟器，基于硬件模拟器进行了攻击验证实验。因芯片可部署网络的规模限制，芯片部署实验采用模型为VGG5，数据集CIFAR-10，编码为直接编码，在不加攻击的情况下，推理精度为83%，加入不同程度的攻击后推理精度损失如表5，由于训练方法的差异，映射过程存在一定转换误差，但是不同攻击强度下的趋势没有大的改变。这也验证了本研究算法的可用性和迁移性。

表5 软件和PKU-NC64C硬件映射adv_loss对比(%)

5 结束语

针对脉冲神经网络对抗鲁棒性分析方法缺乏对网络部署到硬件中的量化过程的损失度量的局限性，本文提出一种将对抗攻击与权重感知量化相结合的训练与推理框架，通过将推理精度损失差、层间脉冲活动和脉冲信噪比作为度量依据，从而衡量量化前后的鲁棒性水平和变化趋势。实验结果表明直接编码的对抗鲁棒性最差，且提出稀疏化的因素对鲁棒性影响相关度为：阈值增加大于权重量化bit降低大于稀疏编码，及单一稀疏性因素对于对抗鲁棒性存在局部最优解的结论，量化方法和评估框架在实际的类脑芯片硬件中得到验证。研究揭示了SNN在量化过程中的部分对抗脆弱性来源和机理，能够帮助研究人员构建更安全可靠的神经形态系统。