NN-EdgeBuilder:面向边缘端设备的高性能神经网络推理框架
2023-10-17张经纬曹新野
张 萌 张 雨 张经纬 曹新野 李 鹤
(东南大学电子科学与工程学院 南京 210096)
1 引言
随着物联网(Internet of Things, IoT)和人工智能行业的发展,神经网络在许多应用场景中的性能已超越传统算法[1,2]。FPGA具有高度可编程性,可以满足应用场景中的延迟、功耗等要求,因此FPGA已成为部署神经网络的流行平台之一[3–5]。目前只有丰富设计经验的硬件研究人员才能在目标平台上部署满足性能目标的神经网络加速器,这阻碍了神经网络的进一步发展。于是各种神经网络前向推理框架不断涌现[6–9],可以解析神经网络算法的高级描述,捕获网络的结构等关键信息,然后自动映射为目标平台的硬件描述。
但是目前主流的神经网络推理框架还没有充分考虑到在边缘端FPGA计算资源有限的情况下,高效地探索设计空间,平衡好资源占用和性能表现,主要还存在下列不足:(1) 很少考虑在边缘端设备计算资源十分有限的情况下,为神经网络定制高效的硬件加速算子,提高资源利用率和性能表现。(2) 忽略了对设计空间探索(Design Space Exploration, DSE)算法的优化,常规的启发式算法对超参数的设置十分敏感,需要多次的实验尝试不同的初始参数。
为了应对上述的挑战,本文设计能够在边缘端FPGA上高效部署神经网络的推理框架NN-Edge-Builder,主要贡献如下:
(1) 设计一个基于数据流结构的神经网络推理框架NN-EdgeBuilder,让神经网络算法领域内的研究人员不需要掌握深厚的硬件加速器设计经验,也可以快速地验证自己设计的网络模块的硬件性能,提高FPGA在神经网络生态中的适用性。
(2) 设计了高效的量化模块,既支持量化感知训练,又支持训练后量化,能够最大限度地保证神经网络的精度。
(3) 开发了通用且高性能的硬件加速算子库,将网络中计算量最大的Conv和FC层映射到Conv/FC层通用计算单元来适应不同的量化位宽和资源限制。
(4) 设计了一个基于多目标贝叶斯优化的设计空间探索算法,使用具有混合核函数的高斯过程作为代理模型可以有效地提取混合设计空间的信息,使用带约束的多目标采集函数来处理边缘端FPGA的资源限制,可以高效地搜索出满足要求的设计点。
本文其余安排如下:第2节介绍推理框架NNEdgeBuilder的总体架构和Conv/FC层通用计算单元;第3节介绍专为NN-EdgeBuilder定制的设计空间探索算法;第4节将讨论我们使用NN-Edge-Builder部署神经网络模型的实验结果;第5节给出结论。
2 神经网络推理框架NN-EdgeBuilder的设计
2.1 推理框架NN-EdgeBuilder的部署流程
本文设计的神经网络推理框架NN-EdgeBuilder能够在边缘端FPGA平台上自动部署神经网络模型,实现检测精度,推理速度和关键资源占用等性能指标的平衡。图1虚线框中的部分展示了NN-Edge-Builder的部署网络模型的完整流程,主要包含网络模型解析,设计空间探索和调用硬件加速算子这3个阶段,具体流程如下:首先网络模型解析模块会解析已经训练好的模型,提取推理阶段网络每层所需的信息,删除冗余信息,接着会进一步配置网络的通用信息,如每层的量化位宽和并行度因子等信息,最后会配置每层的专用信息,如确定每层使用的硬件加速算子等,解析完网络模型之后会输出完整的计算图。
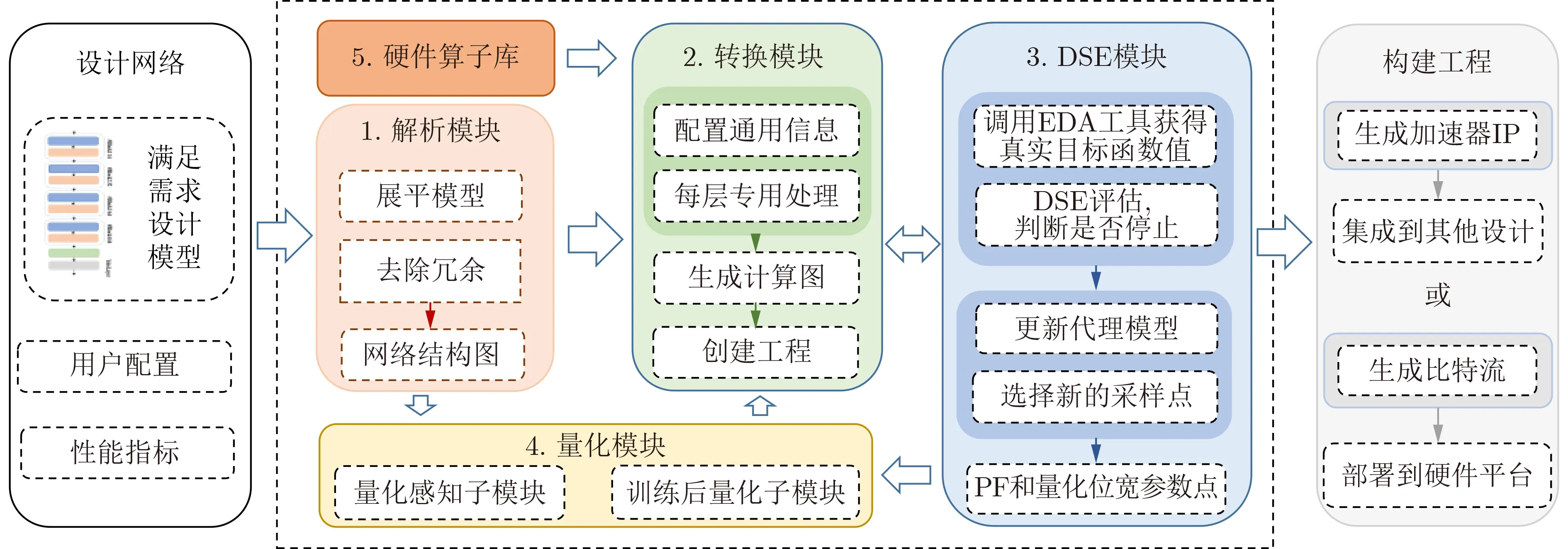
图1 推理框架NN-EdgeBuilder部署网络模型的流程
设计空间探索阶段使用了第3节设计的基于多目标贝叶斯优化的设计空间探索算法,可以探索网络任意层的输出位宽和并行度因子,每次迭代并通过采集函数确定下一个采样点,然后调用EDA工具流得到准确的目标函数值,并以此更新数据集和代理模型,直到满足停止条件,输出帕累托前沿设计点。
硬件加速算子库为推理框架支持的所有网络模块都设计了对应的加速算子,通过计算图连接成一个完整的加速器。针对边缘端FPGA资源有限的现状,本文设计了低推理延迟和低资源占用的FC/Conv层通用计算单元。NN-EdgeBuilder有两种格式的输出:第1种是可以导出加速器的IP并将其集成到更大的设计中。第2种则是生成加速器的比特流,可以直接部署到硬件平台上。
为了能够最大限度地保持推理框架部署加速器的精度,NN-EdgeBuilder的量化模块包含两个子模块,分别支持量化感知训练(Quantization-Aware Training, QAT)[8]和训练后量化(Post-Training Quantization, PTQ)[10]。量化感知训练子模块可以解析经过量化感知训练的网络层,保留其量化配置并固定到计算图中,在设计空间探索阶段这些网络层的权重位宽保持不变,以此利用量化感知训练精度高的特点。训练后量化子模块主要针对推理过程中网络每层的输出位宽量化,由于在保持精度的情况下网络的某些层能够进行更低比特的量化,所以训练后量化子模块采用异构量化,能够在低硬件资源占用的情况下实现高精度。网络每层的输出量化位宽由设计空间探索模块给出,可以细粒度地探索网络每层的输出量化位宽,来达到加速器的最优性能表现。
NN-EdgeBuilder生成的是数据流结构的加速器,会为网络的每一层都例化单独的硬件模块,每一层都会例化单独的缓存器(Buffer)以及基本运算单元(Multiply ACcumulate, MAC),所以每个部分的量化位宽会不一样,对于后续硬件生成的缓存器以及MAC没有影响。图2为推理框架NN-EdgeBuilder部署加速器时的量化流程,其中 IW为输入数据的量化位宽,QW和QB是量化感知训练阶段网络权重和偏置的量化位宽,O W是训练后量化阶段计算层的输出位宽,QA是量化感知训练阶段激活层的输出位宽。量化的整体流程如下:首先量化位宽为IW的输入数据进入计算模块,与位宽为QW和QB的权重和偏置进行计算,得到输出位宽为O W1的中间结果,接着将其送入激活层,得到输出位宽为QA的中间结果,然后就可以进行下一层的运算。

图2 量化模块运行流程
2.2 FC/Conv层通用计算单元
为了能够更好地在资源有限的边缘端FPGA上部署神经网络,本文设计了低延迟,低资源占用的硬件加速算子库。由于Conv层和FC层占据了网络的绝大部分参数量和计算量,接下来重点介绍本文设计的FC层和Conv层通用计算单元,可以利用通用计算单元(GEneral Matrix Multiplication,GEMM)来加速FC层和Conv层。如图3所示,由于本文实现了全片上推理,所以可以直接从Block RAM(BRAM)中加载卷积权重和偏置,只需要从外部存储器读取输入数据,数据流格式的中间计算结果不需要传输到片外存储器中暂存,可以直接传递给下一层。将网络权重加载到Weight Buffer之后,就可以送入通用计算单元。可以考虑对网络进行更低比特的量化来降低存储空间需求,或者设计更加轻量化的网络来完成任务。
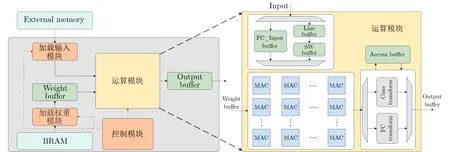
图3 FC/Conv通用计算单元
在开始计算之前,需要根据运算类型对Input的数据进行调整,因为FC层的输入尺寸较小,所以只需要根据输入输出尺寸进行分块并存入到FC_Input Buffer中即可。而Conv层输入尺寸较大且有复杂的数据复用,所以需要将Input中的数据先缓存到Line Buffer中,调整数据排列方式,再传输到SW (Sliding Window) Buffer中,以此来实现流水线运算和输入数据复用。接着将准备好的数据送入到通用计算单元进行运算,接着将计算结果按FC运算和Conv运算分别处理,将计算得到的部分结果对应相加并暂存到Accum Buffer中,最终将完整的输出结果传输到Output Buffer中,然后直接送到下一层网络模块中继续进行计算。以FC运算为例,假设输入的尺寸为 2CI ,当FC层例化了C I个MAC运算单元时,流水线计算过程如下:首先在T=1时 , C I 个通道的输入x1~xCI和神经元参数w1∼wCI并行计算得到C I 个部分结果mi~mCI,并且还将偏置b1加载到Accun Buffer中。同理在T=2 时,再次得到部分计算结果mCI+1∼m2CI,并将T=1时 刻计算得到的m1~mCI累加到A cc1中。
通用计算单元由MAC阵列组成,通过3.1节中介绍的并行度因子控制实例化的MAC数量[11],来决定每一层运算中MAC使用的次数。如果对输入和权重都进行了量化,推理框架NN-EdgeBuilder可以使用查找表(LUT)来实现部分的低位宽乘法来节约DSP资源。NN-EdgeBuilder生成的是数据流结构的加速器,加速器的延迟取决于计算延迟最大的层,所以需要探索每一层的并行度,根据每层的计算量来分配计算资源,实现每一层延迟的均衡。
算法1为全连接运算循环嵌套流程,通常在计算全连接层时会将输入展平为1维向量,即输入向量维度为 CI ,输出向量维度为C O,所以得到一个全连接层输出像素点需要两层循环。本文将FC层的输出维度Loop2展开,实现了输入数据复用,即在一个周期内输入像素点固定,同时和所有输出维度对应的神经元相乘。本文针对输入较小的FC层,使用数组分割指令将FC层的输入数组完全分割到独立的寄存器中,以此实现在一个时钟周期内访问所有的输入。理想状态下经过C I个周期就可得到完整的输出结果。
卷积运算的循环嵌套流程算法2所示,得到一个卷积层输出像素点需要6层循环,针对输入特征图尺寸较大的Conv层,如果将特征图和权重参数全部展开并堆叠成矩阵形式,会占用边缘端FPGA大量的硬件资源。
为了获得最快的卷积运算速度,本文将Loop3~Loop6展开,即实现了卷积核维度的展开,输入通道维度的展开和输出通道维度的展开,整体的并行度为 CO×CI×HF×WF ,在每个周期内输出CO个像素点,对应着输出特征图的同一位置。与FC层一样,Conv层也复用了输入特征图的像素点,这样就可以实现和FC层共用相同的矩阵向量运算单元。
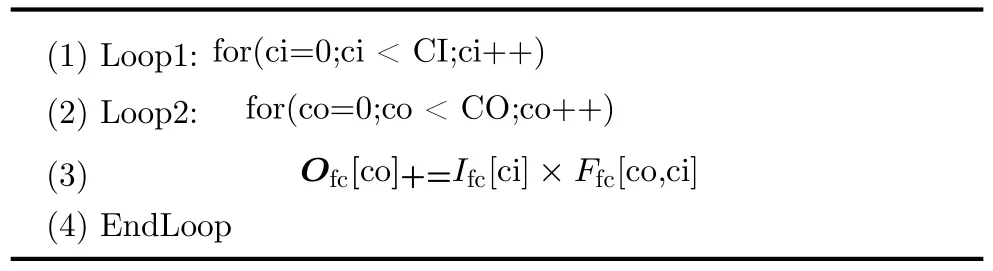
算法1 全连接运算循环嵌套
2.3 Line Buffer和Sliding Window Buffer设计
为了提高输入数据处理速度并节省硬件资源,本文设计了Line Buffer和SW Buffer来缓存输入特征图[12],假设输入特征图的尺寸为 H I×WI×CI,卷积核尺寸为 HF×WF×CI×CO,则Line Buffer的尺寸为 (HF-1)×WI×CI,SW Buffer尺寸为HF×WF×CI。
由于对输入特征图每个通道的处理是相同的,所以为了简洁地说明,图4展示了 CI=1的情况,如图4(a)所示,输入特征图尺寸为HI×WI=5×5 ,卷积核尺寸H F×WF=3×3,所以Line Buffer的尺寸为( HF-1)×WI=2×5,SW Buffer尺寸为 H F×WF=3×3。如图4(b)和图4(c)所示,在T时刻,新的输入像素点x3被压入Line Buffer和SW Buffer的第1行,Line Buffer第1行最先压入的像素点x2被移动到Line Buffer和SW Buffer的第2行,最后是Line Buffer第2行最先压入的像素点x1被 弹出,并压入到SW Buffer的第3行。所以T时刻同一列的3个像素点x1,x2,x3被传入到SW Buffer中,此时SW Buffer是被填满的,所以会将整个SW Buffer的像素点送入运算单元进行一组并行的卷积运算。同理,如图4(d)、图4(e)和图4(f)所示,T+1 时 刻同一列的3个像素点x4,x5,x6被传入SW Buffer中,并再次进行卷积运算。综上分析可得x1,x2,x3一共被复用了3次。从图4(a)和图4(d)可以看出,Line Buffer相当于是在输入特征图上滑动,每次滑动Line Buffer的每行都会压入新的像素点,且将Line Buffer最后一个像素点弹出,这样Line Buffer每次滑动时弹出和压入的像素点正好就是卷积运算所需的一列数据。

图4 Line_buffer工作流程
3 基于多目标贝叶斯优化的设计空间探索算法设计
3.1 NN-EdgeBuilder的参数空间
不同推理框架能够提供不同程度的设计自由度,这些自由度构成了推理框架的参数空间,提供了灵活部署神经网络的能力。NN-EdgeBuilder是基于数据流结构的神经网络推理框架,将网络每一层的关键信息映射成计算图上的节点,通过并行度因子(Parallelism Factor, PF)控制每一层网络例化的基本计算单元的数量,以此来调节并行度。

算法2 卷积运算循环嵌套
并行度因子 PF通 过控制MAC实例化的数量来决定计算层中单个MAC单元使用的次数。如图5所示,输入向量的维度为 1 ×M,神经元参数矩阵维度为M×N,当并行度因子P F=1时会针对每一个乘法实例化相应的MAC单元,则共有M×N个MAC单元,实现了完全并行计算。当并行度因子PF=α时,需要实例化 c eil(M×N/α)个MAC单元。在推理框架NN-EdgeBuilder中量化能够在保持精度的情况下更显著地降低DSP资源利用率,并且支持任意定点数精度。
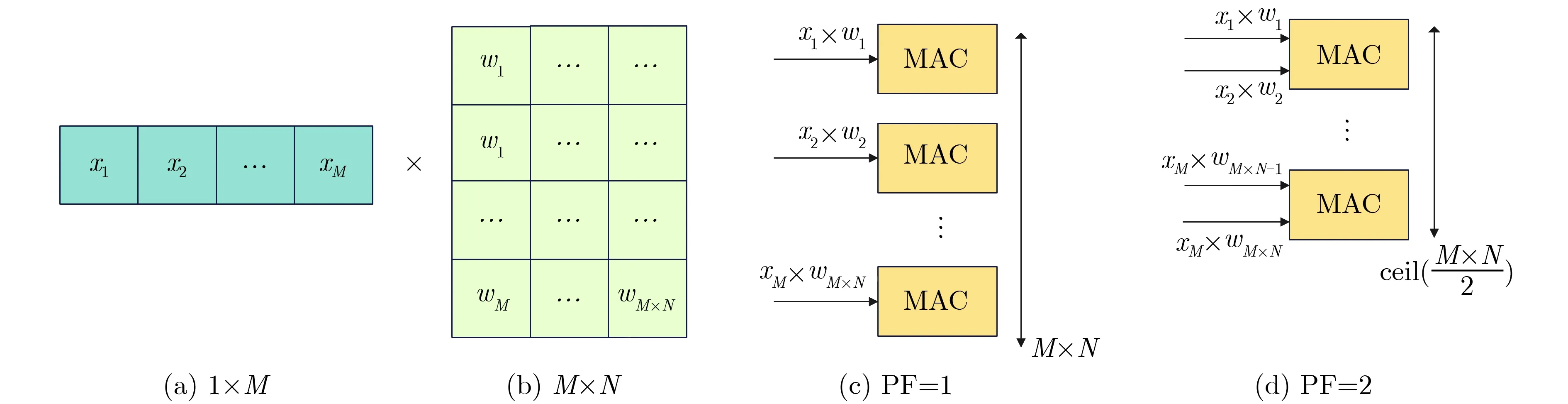
图5 并行度因子控制MAC数量
综上所述,本文选择将网络每一层的并行度因子和输出位宽作为推理框架的设计空间,参数空间的细粒度是可调节的,可以先固定任意层的并行度和量化位宽,然后探索剩余网络层的参数空间,以此来加快探索速度并降低计算资源占用,在满足硬件资源的限制下实现精度和推理速度等指标的平衡。
3.2 具有混合核函数的高斯过程回归
贝叶斯优化使用概率模型来拟合目标函数,因为高斯过程的计算代价相对较小,还可以计算每个设计点的不确定度,所以高斯过程是应用最广泛的代理模型之一[13]。假设已经获得的数据集共有J个神经网络推理框架得到的样本,记为D=(X,Y),其中X=[x1,x2,...,xJ]T是J个已经采样过的设计点,Y=[y1,y2,...,yJ]T是对应的目标性能输出,其中y表示待优化的黑盒函数,记为y=φ(x)。假设φ(x)服 从高斯过程,则可以表示为式(1),其中u(x)代表均值函数,K(x,x)代表核函数。
高斯过程利用核函数来提取不同设计点之间的相似性,所以核函数是决定高斯过程代理模型性能的关键,NN-EdgeBuilder的参数空间为网络每一层的并行度因子和输出位宽,其中并行度因子为整数,而输出位宽表示为
本文针对组合空间构建了具有混合核函数的高斯过程G PM,可以充分地提取组合空间中采样点的相似性。首先使用Matáern核函数来度量并行度因子这样的数值变量,如式(2)所示,其中Kυ第2类修正贝塞尔函数,Γ是伽马函数,l是长度范围,可以通过调整υ来控制核函数的平滑程度,本文取值为2.5,来更好地逼近真实目标值
因为Hamming距离可以有效地度量类别参数之间的距离,所以本文使用基于Hamming距离的加权核函数来提取不同输出位宽之间的相似性[14],如式(3)所示,其中αj为权重超参数,本文取值为1。 当x1,j=x2,j时 ,δ(x1,j,x2,j)=1 ,当x1,j ̸=x2,j时,δ(x1,j,x2,j)=0
综上,针对由并行度因子和输出位宽构成的组合设计空间,本文使用了如式(4)所示混合核函数KMixed(x1,x2)来提升高斯过程拟合目标函数的效率,其中Kcons(x1,x2) 为常量核函数, L为常量,KN(x1,x2)为白噪声
3.3 带约束多目标优化采集函数
在贝叶斯优化算法中采集函数负责确定下一个采样点的位置,来高效逼近最优的目标函数值,目前流行的采集函数之一是期望改进(Expected Improvement, EI)及其多种变体[15],可以结合已经探测得到高确信度的区域和还没有充分开发的区域的信息,实现了搜索和利用两者之间的平衡。
对于带约束的多目标优化问题,假设共有M个目标函数φ(x)={φ1(x),φ2(x),...,φM(x)}和N个约束 条 件C(x)={c1(x),c2(x),...,cN(x)},且φi(x)和ci(x)都满足高斯过程,则多目标优化问题可以表示为式(5)所示。
超体积(HyperVolume,HV)是衡量多目标优化常用的指标[16],以参考点yref为界,超体积是由非支配解集组成的目标空间的体积,记P(V)为帕累托前沿。可以通过帕累托边界上的点P(V)将目标空间分块,使用分段积分来计算期望的超体积改进量(Expected HyperVolume Improvement, EHVI),期望的超体积改进积分是非支配采样点集合的超体积改进分段积分之和。如式(6)所示,其中非支配解集Pn内的设计点不被任何帕累托前沿上的点P(V)支 配,Pn={p ∈Pn:∀y ∈p,y′∈P(V),y′y},P
φx(y)是目标函数预测分布的概率密度函数。
NN-EdgeBuilder需要在满足边缘端FPGA硬件资源限制的条件下自动部署网络模型,常规的EHVI没有考虑有约束多目标优化问题,所以本文使用改进后的EHVI函数,只有在采样点满足约束时才会计算EHVI,改进后的采集函数命名为EHVIC[17]。目标函数和约束条件都是计算代价不菲的黑盒函数,优化后的采集函数由两部分组成,第1部分是针对目标函数的超体积改进量,第2部分则是满足约束的期望C S(p),如式(7)所示
由于是C S(p)是在每个单元格内定义的,所以边界为输入x,记为x={x ∈F:y ∈p},考虑到约束满足高斯过程,可以使用目标函数后验分布的采样点来拟合 Pr(c(x)≤0) 。选择满足(x|y ∈p) 标准的后验采样点,并使用Monte-Carlo采样方法来求解 C S(p),所以EHVIC采集函数的计算如式(8)所示
为了能更快地找到可行解,让高斯过程更专注于利用可行域的信息,不满足要求的点不会用于帕累托集的计算。在多目标贝叶斯优化每次迭代过程中,都是通过最大化EHVIC函数在设计空间F中确定下一次采样点,如式(9)所示
神经网络加速器的核心指标包含检测精度和推理速度、资源占用等,这些指标往往相互冲突,很难同时达到最优。其中边缘端FPGA的硬件资源既可以作为约束条件又可以作为优化目标,例如可以将资源紧张的DSP和LUT作为优化目标,而将其他资源作为约束条件,这样可以探索性能表现的平衡点。
本文提出了基于多目标贝叶斯优化的推理框架设计空间探索算法,具体流程如算法3所示,首先在设计空间内采样,运行EDA工具流得到初始的性能表现样本集Dφ=(X,Y)和硬件资源约束条件集DC={C(x)}。接着在每一次迭代过程中,首先根据样本集Dφ和约束集DC更新代理模型G PM。接着算出非支配域内的期望超体积改进量E HVI(x)和满足约束的期望C S(p),进一步算出带约束的采集函数 E HVIC(x), 然后通过最大化E HVIC(x),选择下一个参数配置点xJ+1。得到新的配置点之后继续运行EDA工具得到真实的性能表现函数值φ(xJ+1)和硬件约束C(xJ+1)。最后更新数据集和约束集并进行下一次迭代。迭代的停止条件可以根据实际场景的需要来选择,如设计空间探索的最大时间,参考帕累托前沿的ADRS等,最终输出加速器精度和推理速度平衡的帕累托前沿设计点。

算法3 贝叶斯优化算法流程
4 实验结果及分析
为了验证NN-EdgeBuilder自动部署的加速器的性能,针对大疆(DJI)无人机小目标检测数据集,本文使用NN-EdgeBuilder部署UltraNet网络。为了提高生成的UltraNet网络加速器的性能,本文使用量化感知训练,位宽设置为4 bit,并通过数据增强,重参数化等优化策略,在不改变UltraNet推理阶段参数量和计算量的情况下将精度提升到了0.703。网络训练完成之后,就可以使用NN-Edge-Builder将其自动部署在边缘端Ultra96-V2 FPGA上,工作频率为250 MHz。NN-EdgeBuilder通过设计空间探索给出2个帕累托设计点,分别记为P1和P2点,然后可以部署到Ultra96-V2开发板上来测试结果。
本文将NN-EdgeBuilder经过设计空间探索得到的UltraNet-P1和UltraNet-P2加速器与专用加速器SEUer和ultrateam进行对比,表1为4个加速器分别处理5.25×104张图片的性能表现,对每一个加速器,循环测试5次取各个指标的均值。
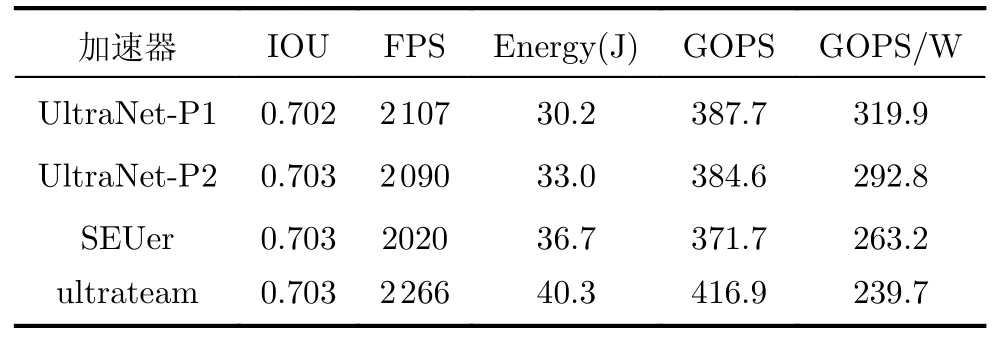
表1 UltraNet加速器性能对比
UltraNet-P1加速器每秒处理图片的数量比ultrateam加速器少159帧,但是UltraNet-P1使用了高性能的硬件加速算子,处理5.25×104张图片的功耗仅为30.2 J,功耗比ultrateam降低了25.06%。UltraNet-P1拥有最高的能效比,其每瓦特每秒的运行数达3.199×1011次,比ultrateam提升了33.46%。
UltraNet-P2加速器实现了检测精度和推理速度的平衡,UltraNet-P2的IOU和SEUer相同,都是0.703,其余性能指标均优于SEUer,其中推理速度提升了70FPS,功耗表现提升了10.08%,能效比提升了11.25%。
UltraNet-P1和UltraNet-P2优秀的性能表现证明了推理框架NN-EdgeBuilder能够有效地将网络模型映射为高性能的硬件加速算子,再通过充分的设计空间探索,生成性能优异的神经网络加速器。
从表2可以看出目前主流推理框架支持的深度学习框架数量有限,如DNNBuilder只支持Caffe框架,而NN-EdgeBuilder 的扩展性更强,能够高效地解析主流深度学习框架设计的网络模型,如PyTorch和TensorFlow。表2还对比了NN-Edge-Builder和其他推理框架部署VGG网络的性能表现,目前主流的推理框架支持的量化精度通常在8 bit及以上,对低比特量化没有很好的支持,而NN-EdgeBuilder支持量化感知训练,所以可以进行4 bit量化并保持网络精度。NN-EdgeBuilder的硬件加速算子库提供了低延迟低功耗的算子和高性能的DSE算法,所以针对相同的FPGA平台,NNEdgeBuilder 生成的VGG加速器计算性能是Deep-Burning-SEG的两倍。由于DNNBuilder在硬件资源更丰富的平台上部署,并且对VGG进行了剪枝,所以生成的加速器计算性能超过了NN-EdgeBuilder。但是NN-EdgeBuilder主要针对边缘端FPGA进行优化,考虑了低功耗和低资源占用,所以生成的加速器能效比是DNNBuilder的4.4倍,DSP的计算效率提升了50.65%。所以与目前主流的推理框架相比,NN-EdgeBuilder针对边缘端FPGA生成的加速器解决方案实现了明显的性能提升。
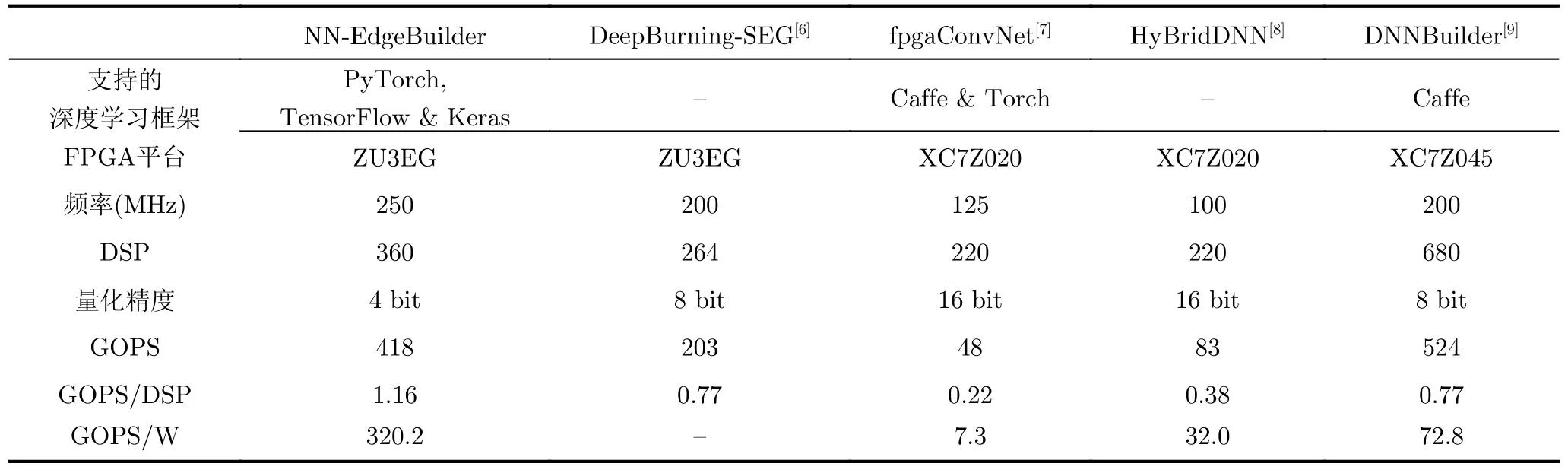
表2 NN-EdgeBuilder和其他推理框架部署VGG网络的性能对比
5 结束语
目前将神经网络部署在FPGA平台还面临开发时间长、性能优化难等问题,本文设计了神经网络推理框架NN-EdgeBuilder,提供了高性能的基于多目标贝叶斯优化的设计空间探索算法和低延迟低功耗的硬件加速算子,能够加速开发对边缘端FPGA友好的神经网络硬件加速器,生成的加速器比目前主流的推理框架有显著的性能提升。
