单向及双向布篾工程竹材-钢填板连接件力学性能研究*

李 智 李百鹏 彭 洋 王 睿

(1.浙江大学建筑工程学院,杭州 310058;2.浙江大学平衡建筑研究中心,浙江大学建筑设计研究院有限公司,杭州 310058;3.南京工业大学土木工程学院,南京 211816;4.浙江大学-伊利诺伊大学厄巴纳香槟校区联合学院,浙江海宁 314400)

0 引 言

竹材具有很高的比强度,通过优化布篾而制备的工程竹板材是环保高效的结构工程材料[1-3]。销连接是在现代竹木结构中广泛使用的标准连接方式之一。但囿于竹木材料横向断裂性能的限制,在实际工程中往往会发生节点域的脆性断裂破坏[4-5],节点域的强度和刚度则对整体结构起控制性作用。同时,竹木结构简易化装配施工的要求,还对现代竹结构节点域的加工便利性和性能可靠性提出了新的要求。

目前,工程木结构领域相关研究主要集中在销连接及其失效模式之上[6]。其可采用钢销[7]、螺栓[8]、圆钉[9]甚至竹销[10]作为连接件。而采用螺栓作为连接件的又称为螺栓连接,是在工程实践中应用最广泛的连接形式,并主要分为钢填板[11](木-钢板-木)和钢夹板[12](钢板-木-钢板)两大类。在合理的几何参数限制条件(如钢板厚度、螺栓直径、节点域端距、边距、中距等)之下,销连接将因为销槽在一定长度上达到其销槽承压强度fh或销钉自身在弯曲应力作用下达到其屈服强度fy,形成塑性铰(对应的弯矩值为My)而失效。上述销槽承压屈服和销弯曲屈服都具有一定的塑性,故上述连接的失效模式往往又被称为屈服模式,并可通过相应的屈服模型,如欧洲屈服模型(European Yield Model,EYM)[9],对连接件的承载能力进行估算。而针对各种不同的连接件形式,去研究其对应的几何参数设计条件,保障上述塑性屈服模式的实现,避免节点域的横向断裂失效,则是目前工程木结构领域相关研究的主要内容之一。

目前针对工程竹结构节点域的研究还比较缺乏,而竹材又是一种各向异性与脆性表征明显的材料。相关研究[4-5]表明：单向工程竹材在采用远大于GB 50005—2017《木结构设计规范》所规定的端距、边距与中距的构造要求后,仍然发生了节点域的行剪与劈裂破坏。可见,工程竹材连接件设计要求与工程木结构具有显著差异,难以仅通过几何参数限制条件就保证其塑性破坏模式。有鉴于此,本研究针对在现代工程竹结构中使用较为广泛的钢填板螺栓连接,以及具备简易快速施工优势的压铆空芯铆钉连接[13]的力学性能进行试验研究及理论分析,以期为上述连接件在工程竹结构中的设计和应用提供支撑。

1 材料与方法

1.1 工程竹材及其坐标

竹材是一种具备细观梯度结构的天然生物质复合材料[14]。竹篾中的维管束单元是竹材刚度与强度的主要来源。维管束分布密度从竹杆外壁至内壁呈一定规律降低,以适应竹子侧向受力与压弯受力的需求。以竹篾为基本组成单元的工程竹板材的材料性能显然也具备上述性质,即材料性能与方向相关。所以,可通过区分工程竹材中维管束分布的主要方向去定义工程竹材的主纤维方向及其他方向。

图1是本研究所涉及的竹材及其坐标体系。针对原竹杆件,可定义竹材生长方向为径向L,原竹杆件剖面上某一点指向该点曲率中心的方向为R方向,该点对应的切线方向为T方向。由此,就建立起了分析原竹杆件力学性质的LTR坐标系统。原竹杆件破篾而形成的竹篾,是制备工程胶合竹板材的主要原材料。针对竹篾,可定义竹纤维的方向为1方向,垂直于竹纤维的方向为2方向,竹篾厚度方向为3方向。由此,就建立起了分析单个组坯用竹篾的123坐标系统。上述竹篾针对具体的建筑与结构性能要求,通过布篾、组坯胶合以后,就可以形成工程竹板材。针对工程竹板材,可定义布篾较多的方向为主纤维方向x,布篾较少或未布篾的方向为次纤维方向y,厚度方向为z。由此,就建立起了分析工程竹板材的xyz坐标体系。在上述坐标体系下,表1给出了本研究所取用的工程竹材的主要力学性能。

表1 工程竹板材的主要力学性能[3]Table 1 Mechanical properties of engineered bamboo panels

图1 工程竹材及其坐标体系Fig.1 Engineered bamboo and its coordinator system

销槽承压强度是竹木结构销类连接件计算的重要变量。本研究采用ASTM D5764-97a (2013)中的半孔法[15]对上述两种工程竹板材在x和y方向的销槽嵌入性能进行了研究。

通过如图2所示的工程竹材销槽嵌入曲线,并通过ASTM规程[15]中所规定的相应计算方法,可以计算出板材的销槽承压强度数值(表2),其中括号中的数值为标准差。

表2 工程竹板材的销槽承压强度Table 2 Embedment strength of engineered bamboo panels

图2 工程竹材销槽嵌入曲线Fig.2 Embedment curves of engineered bamboo panels

1.2 钢填板及连接件的材料性能

本研究用钢填板沿顺轧制方向取样,试件制作方法和试验方法以及数据处理方法遵照GB/T 228.1—2010[16]的要求。具体尺寸如图3所示。试验结果如表3所示。由上述材性试验数据分析得到,试验所使用的Q345钢材料满足GB/T 700—2006碳素结构钢[17]的各项强度要求。

表3 钢填板材料性能参数Table 3 Material properties of steel plate

Ra为表面粗糙度。图3 Q345钢材拉伸试件尺寸 mmFig.3 Dimensions of Q345 steel tensile specimens

本研究所采用的螺栓连接件是直径为8 mm和10 mm的半螺纹螺栓,螺栓强度等级为4.8级和8.8级,无螺纹区域长度不小于56 mm。所采用的304不锈钢空芯连接件外径为10 mm,壁厚分别为0.8,1,1.5 mm。参考ASTM F1575-17规范[18]提供的屈服强度测试与计算方法,对螺栓和空芯铆钉进行三点弯曲试验,测试螺栓的屈服强度和空芯铆钉的塑性弯矩。试验装置如图4所示,荷载-位移曲线如图5所示。测试结果汇总如表4所示。

表4 连接件弯曲屈服强度试验结果Table 4 Test results of the bending yield of connections

图4 连接件三点弯曲试验加载装置Fig.4 Test set-up of three-point bending for connections

注：4.8-8/10表示强度等级为4.8级、直径为8/10 mm的螺栓,8.8-10表示强度等级为8.8级、直径为10 mm的螺栓,10×0.8/1/1.5表示外径为10 mm、壁厚为0.8/1.0/1.5 mm的空芯连接件。图5 连接件三点弯曲试验荷载-位移曲线Fig.5 Load-displacement curves of the three-point bending of connections

1.3 试验设计及加载方式

研究变量如图6a所示,主要涉及竹材类型、销连接件类型以及节点域相应的几何变量。相对应的实验矩阵如表5所示,其中空芯铆钉连接件主要考虑了三种不同壁厚的影响,螺栓连接件尺寸与某实际钢-竹组合结构网架相同。相关试件在室内标准养护条件(室温20 ℃,相对湿度65%)下养护48 h以上。连接试件通过设计的夹具与万能试验机相连,施加的荷载与位移由试验机自动记录。同时,在连接试件两侧安装位移传感器(LVDT),与试验机同步进行位移测量,如图6b所示。

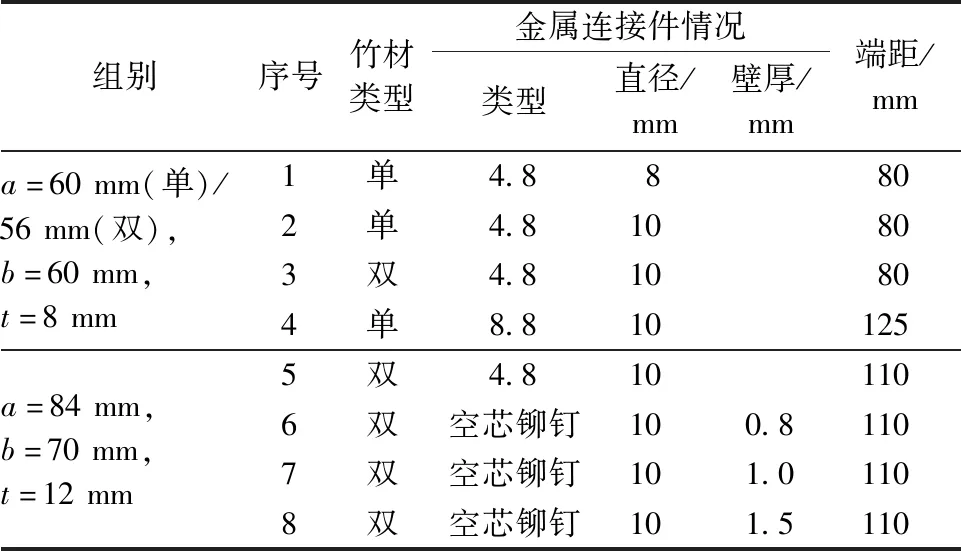
表5 竹-钢-竹连接件试件情况Table 5 Test matrix of bamboo-steel-bamboo connections

a—试件变量信息;b—加载装置示意。图6 竹-钢-竹连接试验详情Fig.6 Test details of bamboo-steel-bamboo connections

针对每组试件,进行了三次单调试验和一次滞回试验。单调试验参考ASTM D5652-15[20]的加载制度进行。首先对夹持好的试件进行预加载,大小为0.3F(F为预估承载力),使试件被拉紧;然后,调整好变形测量装置的位置,并将力传感器的显示调零;最后,调整好试验机的速度,并开始对试件进行拉伸。以位移控制对试件进行受拉方向的单调匀速加载,加载速率为1 mm/min,以保证试件从加载到破坏的时间不少于5 min且不大于20 min。滞回试验参考CUREE(Consortium of Universities for Research in Earthquake Engineering)加载制度[21],但是并不施加反方向压力。加载速率为3 mm/min。其中参考位移Δ=0.6Δm,Δm为单调试验中荷载下降至0.8Fmax时所对应的位移值。对于荷载没有降至0.8Fmax就发生破坏的情况,Δm则取破坏时对应的位移值。滞回加载程式分四组：第一组以0.05Δ加载幅度各进行6次往复加载,第二组以0.075Δ和0.1Δ幅度各进行7次往复加载,第三组以0.2Δ和0.3Δ幅度各进行4次往复加载,第四组以0.4Δ、0.7Δ、1.0Δ和2.0Δ幅度各进行3次往复加载。

2 结果与分析

2.1 破坏模式

如图7所示,单向布篾胶合竹材试件最终破坏表现为竹材劈裂破坏和螺栓屈服,双向布篾胶合竹材最终破坏表现为竹材销槽承压破坏和金属连接件屈服。在弹性阶段,连接件未发生塑性变形,连接件与螺栓孔道上表面完全贴紧且同时受到钢填板与竹材的压力,当连接件达到其弹性抗弯强度时开始弯曲,形成塑性铰,构件开始进入塑性阶段。随着塑性变形的发展,靠近钢填板处的连接件对螺栓孔的压力逐渐增大,远离钢填板端的连接件对螺栓孔压力逐渐减小甚至与孔道分离。

a—序号1-单-4.8/8/80;b—序号2-单-4.8/10/80;c—序号3-双-4.8/10/80;d—序号1-单-8.8/10/125;e—序号5-双-4.8/10/110;f—序号6-双-10;0.8/110;g—序号7-双-10;1/110;h—序号8-双-10;1.5/110。4.8/8/80表示4.8级直径8 mm的螺栓连接件,端距为80 mm;10;0.8/110表示直径为10 mm、壁厚0.8 mm的空芯连接件,端距为110 mm。图7 竹-钢-竹连接件试件破坏模式Fig.7 Failure modes of bamboo-steel-bamboo connections

从图7a、图7b、图7d中可以看出,螺栓连接件出现明显的弯曲,螺栓孔呈现左右对称的梯形,其他区域的螺杆仍然笔直,胶合竹材被挤压沿着纤维部位呈现劈裂破坏。在塑性铰之外的部分,螺栓变形较小,试件受力较小,单向布篾胶合竹材劈裂以及螺栓屈服导致试件破坏,螺栓和胶合竹材间有一道或者数道贯穿的裂缝,为典型的单铰屈服失效模式。双向布篾胶合竹材销槽承压破坏与金属连接件屈服破坏同时发生,螺栓连接件屈服弯曲,空芯铆钉局部被压扁,其中壁厚较小的试件为双铰屈服失效,壁厚较大的试件为单铰屈服失效。

2.2 力-位移曲线

竹-钢-竹连接件的单调力-位移曲线的平均曲线及其相应的滞回曲线如图8所示。通过上述曲线可知,连接件由于初始孔壁间隙的影响,滞回加载时在0～2 mm位移段有一定的低刚度滑移。本试验的滞回曲线保留了上述初始滑移段。金属连接件与孔壁接触后,则进入了连接件受力的第二阶段,其性能主要受金属连接件的弯曲屈服性能和竹基材的嵌入性能而决定。通过观察滞回曲线可以发现,钢-竹连接件在同一加载行程的第二次及第三次加载中,出现了比较明显的颈缩现象。这种现象主要是由于竹材不可恢复的损伤而造成的。当进入破坏阶段时,双向竹材的延性性能显著优于单向竹材,其较为充分地发挥了金属材料延性较好的特征。同时,当空芯钢管壁厚为1.5 mm时,连接件的承载力和耗能能力均优于采用4.8级螺栓的连接件。

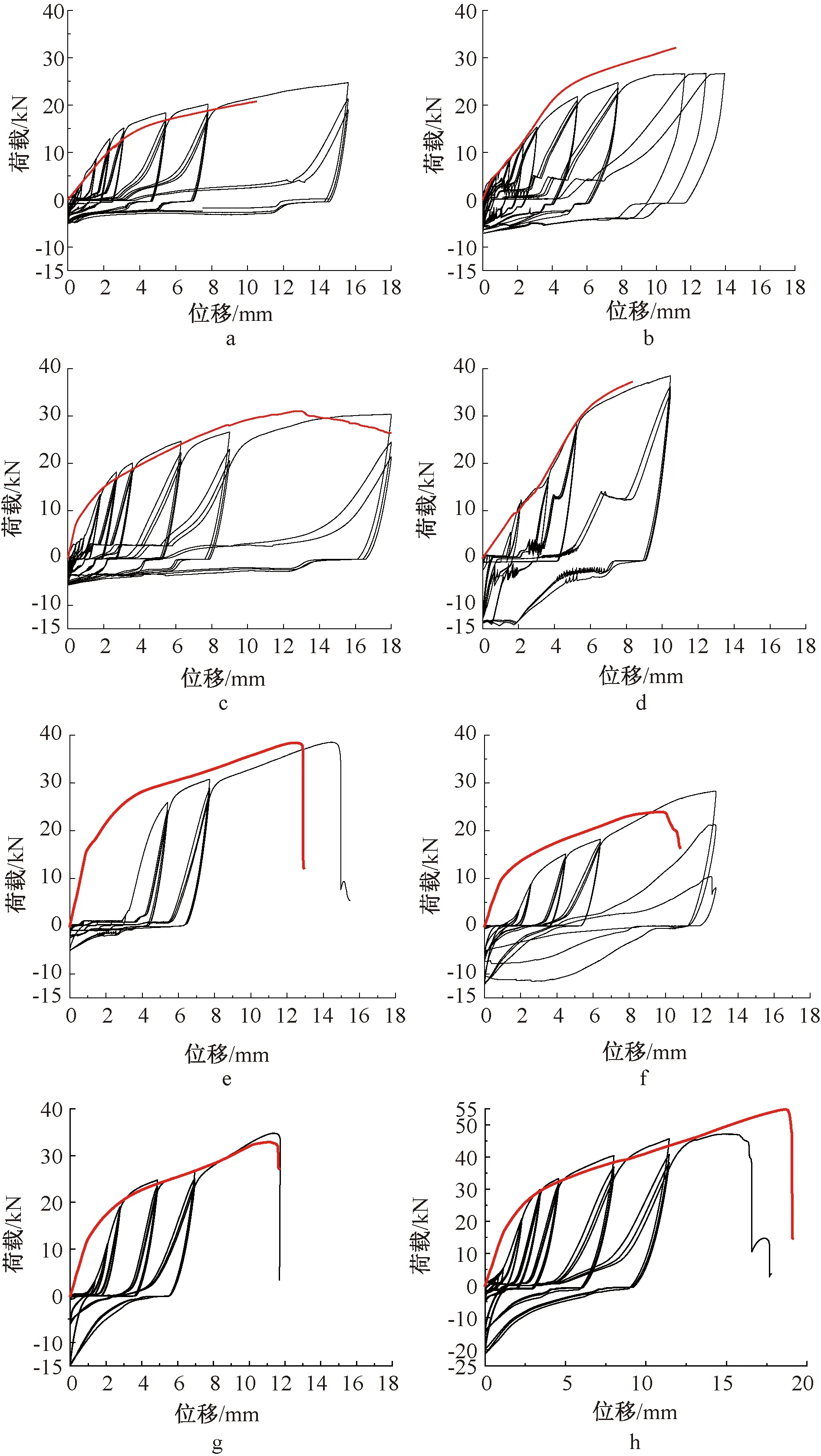
a—单向竹材,4.8级8 mm螺栓,端距80 mm;b—单向竹材,4.8级10 mm螺栓,端距80 mm;c—双向竹材,4.8级10 mm螺栓,端距80 mm;d—单向竹材,8.8级10 mm螺栓,端距125 mm;e—双向竹材,4.8级10 mm螺栓,端距110 mm;f—双向竹材,直径10 mm壁厚0.8 mm空芯柳钉,端距110 mm;g—双向竹材,直径10 mm壁厚1 mm空芯柳钉,端距110 mm;h—双向竹材,直径10 mm壁厚1.5 mm空芯柳钉,端距110 mm。图8 竹-钢-竹连接件力-位移曲线Fig.8 Load-displacement curves of bamboo-steel-bamboo connections

2.3 主要力学性能参数

通过上述试验所获取的荷载-位移曲线可以计算出竹-钢-竹连接件得初始刚度Ke、屈服荷载Fy、极限荷载Fu、屈服位移Δy、极限位移Δu及延性系数λ等力学性能参数。但是如何合理界定竹木结构构件与连接件的“屈服”状态,则尚缺乏普遍共识[22]。

各参数定义与计算方法如下：初始刚度Ke为不考虑初始滑移段的曲线上升段10%～40%峰值荷载的割线刚度;屈服荷载Fy为画一条平行于初始刚度的直线,然后将其偏移5%螺栓直径,偏移线与荷载-位移曲线相交的荷载即为屈服荷载[15],如果5%偏移线不与荷载-位移曲线相交,则把极限荷载取为屈服荷载;极限荷载Fu取为试验中记录的最大荷载;屈服位移Δy为屈服荷载所对应的位移;极限位移Δu为极限荷载所对应的位移;延性系数λ为极限位移与屈服位移的比值。基于滞回曲线外包络线所计算的竹-钢-竹螺栓/空芯压铆钢管连接件的主要力学性能参数见表6。

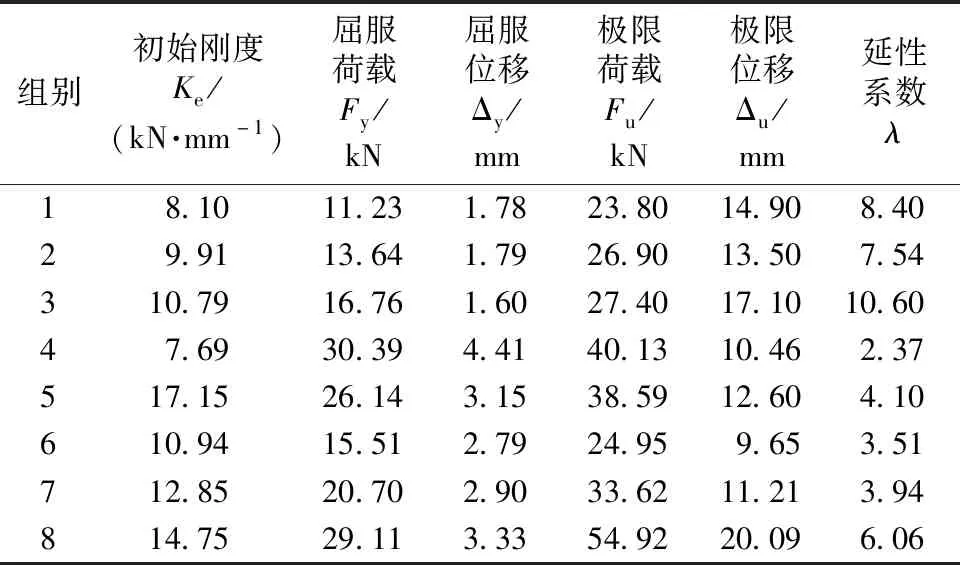
表6 竹-钢-竹连接件主要力学性能参数Table 6 Mechanical properties of bamboo-steel-bamboo connections

由表6可知：极限荷载、屈服荷载随着螺栓直径的增大而增大,胶合竹材螺栓连接件的螺栓直径从8 mm变为10 mm时,螺栓连接的屈服荷载和极限荷载分别提高了21%和13%。双向布篾竹材的极限荷载、屈服荷载、延性系数均大于单向布篾胶合竹材,比较2组和3组试件,双向布篾胶合竹材的初始刚度略高于单向布篾胶合竹材,屈服荷载、极限荷载和延性系数分别提高22.9%、1.9%和40.6%。综上所述,双向布篾胶合竹材的螺栓连接和空芯铆钉连接节点承载能力相对最好,所以在实际工程中,双向布篾胶合竹材应用更为广泛。

比较5、6、7、8组,可以发现10 mm直径1 mm壁厚空芯铆钉承载能力与10 mm直径4.8级螺栓接近,随着空芯铆钉壁厚的增大,空芯铆钉的极限荷载、屈服荷载、初始刚度和延性系数均有提高,当壁厚从0.8 mm变为1.5 mm时,极限荷载、屈服荷载和延性系数分别提高120%、87.7%和72.6%,合适的径厚比可以提高空芯铆钉连接的承载能力,对于10 mm直径的空芯铆钉,建议径厚比取6.7。

3 承载力估算方法与结果

3.1 屈服与破坏模型

欧洲屈服模型是目前多个国家木结构设计规范与标准[23-25]给出的销连接件计算方法的基础,也被称为Johansen屈服理论[26]。其假设成立的前提如前所述：是基于销槽承压屈服和销弯曲屈服的塑性表征。上述理论对于脆性表征明显的工程竹材是否适用,则需要通过相应的试验研究验证。

如图9所示,是根据试验观测到的破坏模式,在欧洲屈服模型的基础上所给出的竹-钢-竹连接件延性屈服破坏模型。假设金属连接件形成单个塑性铰,达到其如前文所测的屈服弯矩My。在此基础上,选取金属连接件为隔离体进行力学分析,并假设竹材达到其销槽承载强度fh,并均匀分布在金属连接件上。金属连接件由于拉索效应而产生的轴向拉伸力,则受连接件拉伸屈服强度fty和竹材z面局部抗压强度fcz控制。在上述假设的前提下建立力学平衡方程[9],则可估算出竹-钢-竹连接件在延性破坏模式下所对应的承载力。

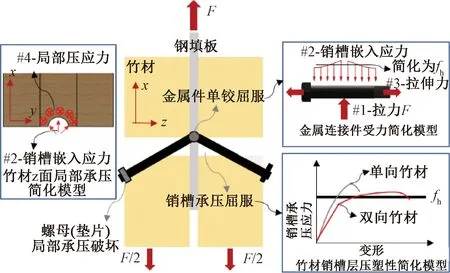
图9 竹-钢-竹连接件延性屈服破坏模型Fig.9 Ductile failure model of bamboo-steel-bamboo connections

同时,试验中针对单向竹材,还观测到了剪切和劈裂破坏,其相应的脆性破坏模型如图10所示。对于劈裂破坏而言,其可归因于孔边复杂的应力状态,并主要受y方向的拉伸应力控制,从而简化为I型断裂问题进行分析。对于行剪破坏而言,则主要受沿着x方向且法线方向为y方向的剪切应力控制,从而可简化为Ⅱ型断裂问题进行分析。而具体求解上述应力值,则可以通过假设对称于脆性劈裂/剪切破坏面的一半竹材隔离体为欧拉-伯努利梁[27]或铁木辛科梁[28],梁的中性轴位于隔离体的中间位置,在开孔位置承受外力F由于楔入效应而产生的y方向的分力V,以及F所产生的弯矩M的作用。同时,其放置于基础刚度为K的文克勒(Winkler)地基之上。基于上述模型假设,并通过相应的力学计算方法,就可以估算出相应的拉伸应力σy[29]和剪切应力τxy[28],进而在相应的强度/破坏理论假设下,计算或通过有限元法模拟出上述脆性破坏模式下所对应的承载力。

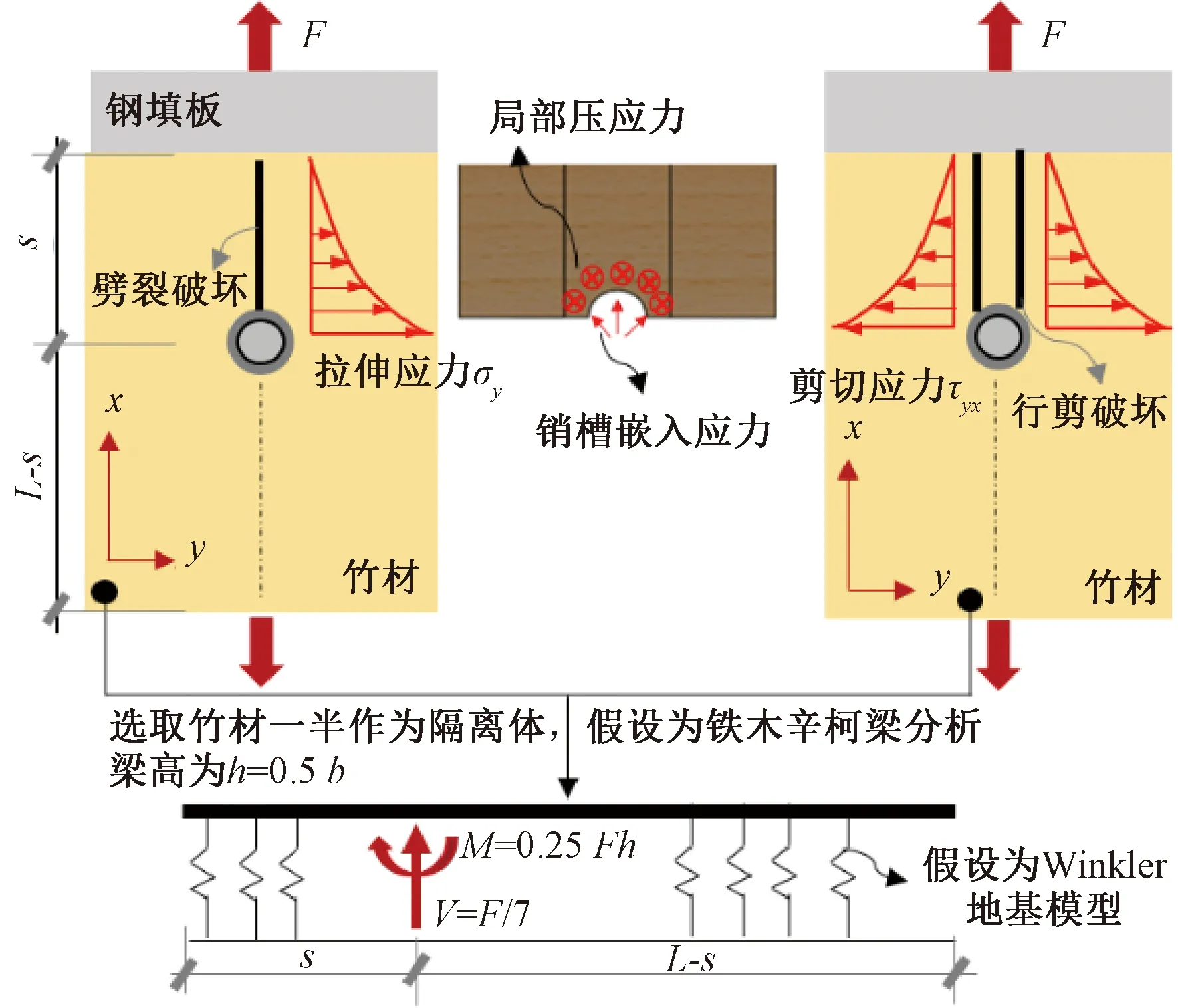
图10 竹-钢-竹连接件脆性断裂破坏模型Fig.10 Brittle failure model of bamboo-steel-bamboo connections

3.2 单栓连接承载力估算公式

竹-钢-竹单栓节点域发生连接件的单铰屈服破坏与竹材的销槽承压破坏时,可通过上述力学模型与平衡方程,计算出其屈服承载力为[9,24]：

(1a)

Fax,R=min(fyAs,fczAr)

(1b)

式中：fh为竹材主纤维方向(x方向)的销槽承压强度,取值如表2所示;t1为每个计算剪面所对应的竹材厚度,本文取为(a-t)/2,取值如表5所示;d为销连接件直径,取值如表5所示;My为销连接件名义屈服弯矩,取值如表4所示;Fax,R为销连接件考虑拉索效应所对应的抗拔出力,取为销连接件的抗拉屈服强度fy乘以截面净面积As和竹材在z方向的抗压强度乘以垫片面积Ar之间的小值。

连接件发生劈裂破坏时的承载力,可认为主要受竹材次纤维方向(y方向)抗拉强度fty的控制,其抗劈裂承载力可通过下式计算[30-33]：

Rsplit=ksftysti

(2)

式中：ks为考虑了通过梁模型计算后获知的F与V之间的关系(β=V/F,亦被称为楔入系数)、启裂位置、及各种应力(以y方向正应力σy和剪应力τxy为主)交互作用后的系数,可取为1/0.3[29,31];fty为竹材在y方向的抗拉强度,取值如表1所示;s为连接件的端距,取值如表5所示;ti为竹-钢-竹连接件区域竹材厚度a扣除钢板厚度t后的计算厚度,取值如表5所示。

连接件发生行剪破坏时的承载力,可认为主要受竹材剪切强度fv的控制,其抗剪承载力可通过下式计算[30-33]：

Rv=2kvfv,yxsti

(3a)

(3b)

式中：kv为行剪破坏计算系数;fv,yx为竹材沿着x方向且法线方向为y方向的剪切强度,取值如表1所示。Gyx为与上述剪切强度所对应的剪切模量,建议取为550 MPa[34];Ex为竹材在x方向的弹性模量,取值见表1。

本研究所涉及的单栓连接件的承载力估算值,则应是式(1)～式(3)中的最小值。且出于节点延性变形的考虑,宜使得式(1)所估算出的延性承载力为最小[33,35-36]。按上述单栓承载力估算公式进行计算,8组试件的承载力如表7所示。

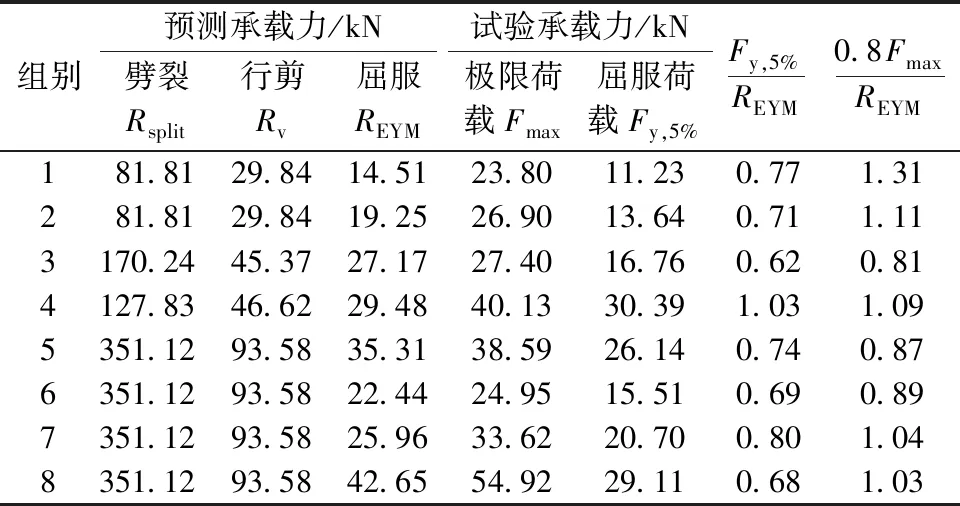
表7 不同屈服、破坏模型下的承载力与试验值对比Table 7 Comparisons of bearing capacity values based on different failure modes and the test results

同时值得注意的是,上述基于欧洲屈服模型而获取的承载力值对应了试件力-位移曲线中的某一具体荷载值,并非连接件承载力的极限状态,而更接近于工程设计的“屈服”状态。表7采用了5%偏移法给出了屈服荷载,同时目前还有研究取用力-位移曲线中0.8倍极限荷载所对应的值为屈服荷载[36]。对比试验获得的屈服荷载结果和理论分析结果可知,5%偏移法计算所得的屈服荷载略低于理论分析值。若采用0.8倍极限荷载作为试验屈服荷载值,则其更接近于理论值。

4 结束语

针对单向及双向布篾工程竹材-钢填板螺栓和空芯铆钉单销连接件进行了试验研究与理论分析,得出以下主要结论：

1)双向布篾工程竹材-钢填板普通螺栓/空芯铆钉连接以钢材的屈服破坏为主,连接节点域承载力的离散性较小,双向布篾竹材有效地避免了节点域横向断裂破坏的发生,承载力相对较好,建议在节点域等复杂力学环境中使用双向布篾竹材。在使用单向布篾竹材时,建议校核其脆性破坏承载力,并通过合理的几何参数设计,使其大于按屈服模型所估算的延性屈服承载力。

2)空芯压铆连接具有施工便利、施工效率高等优点。试验研究表明：1 mm壁厚不锈钢空芯压铆钢-竹连接的力学性能与采用10 mm直径的4.8级普通螺栓连接相近,随着空芯铆钉的径厚比减小,空芯铆钉连接的极限荷载、屈服荷载、初始刚度均有所提升,对于10 mm直径的空芯铆钉,建议径厚比取6.7,该新型连接具有较好的工程应用潜力。

3)通过连接屈服模型可以对钢-竹连接的屈服承载力进行估算,并可在其基础上实现对连接的工程计算与设计。