基于突变理论的空间钢结构稳定性研究

2023-10-16王健李红民闫凯

山东建筑大学学报 2023年5期

王健李红民闫凯

(1. 山东建筑大学信息与电气工程学院，山东济南 250101；2.山东建筑大学土木工程学院，山东济南 250101)

0 引言

空间结构因跨度大、抗震性能好等优点已广泛应用于体育场馆、会展中心、铁路站房等公共建筑形式。随着服役年限的增加，在材料劣化、环境侵蚀、随机荷载等因素的影响下，结构构件不可避免地会产生损伤，空间钢结构杆件众多，具有较高的超静定次数，关键构件的失效会导致结构失稳，造成突然倒塌的事故。结构稳定性是力学中研究的热点问题，学者们对结构稳定性作了大量的理论研究，如经典的特征值稳定理论、临界点稳定理论等，较有影响的判定准则有BUDIANSKY 和ROTH 提出的B-R 运动准则、能量准则、李雅普诺夫(Lyapunov)稳定理论判别准则等[1]。但从工程应用的角度来看，现有的理论研究方法在实际应用中均存在不同的限制条件。

为了预防既有建筑结构安全性事故，大量工程建立了结构健康监测系统。结构安全评估作为健康监测系统的组成部分，可分为包括层次分析法、极限分析法的确定性方法和包括构件可靠度分析法、体系可靠度分析法的可靠度分析方法[2]，但准确、高效地利用海量监测数据进行结构稳定性分析和安全评估还需深入研究。 RAFIEI 等[3]建立了基于深度学习的整体和局部结构评估模型，以加速度频谱作为深度限制波兹曼机的输入，隐含层提取的特征用来确定结构健康程度。 BAO 等[4-5]通过机器学习利用所获数据进行结构的损伤识别和状态评估，提出了结构健康监测数据科学与工程的研究方向。朱宏平等[6]提出精准复杂结构精准体检技术，通过检测关键局部区域结构评估结构健康状态。贺海建等[7]以海口东站钢结构雨棚健康监测为例，建立了单只传感器的三级阈值预警。杨渊等[8]基于长短期记忆神经网络模拟评估了凯威特型(K6)网壳屋盖结构。罗尧治等[9]和熊仲明等[10]以层次分析法为基础运用模糊综合评价法对大跨度空间钢结构进行了综合评估。

突变理论是研究系统从一种状态跳跃到另一种状态的数理方法，非常适合于空间钢结构因构件失效、承载能力骤降而失稳的问题分析。目前，该理论已在大坝、隧道等工程结构中开展应用研究，并取得了丰硕成果[11-13]。通常，应变速率作为反映结构动力学特性的指标，在结构动力响应中具有重要作用，关于钢结构应变速率效应的研究，陈俊岭等[14]揭示了材料强度和弹性模量会随着应变速率的增加而提高。但现有研究并未涉及应变速率效应对既有结构稳定性的影响，同时鲜见以结构健康监测系统为依托针对空间钢结构稳定性判据研究的相关文献。

文章依托潍坊北站南站房为工程背景，基于突变理论建立空间钢结构杆件失稳的尖点突变模型，推导出钢结构杆件失稳动力学判据；采用主成分分析法对应变传感器监测数据降维并提取结构特征数值；利用突变级数法对结构稳定性进行综合评估，通过实例分析，验证了所提方法的有效性。

1 空间结构稳定判据理论

1.1 动力学模型反演

空间钢结构自由度较多，根据显式物理量判别结构稳定性更具有实际意义[15]。外界荷载作用下结构发生失稳时，结构单元应变能发生突变，应力、应变将突然跳跃较大数值。将应变速率-时间序列作为结构非线性动力模型的已知特解，反演出结构应变速率的非线性动力模型。

将应变速率作为结构动力学系统的变量X，动力学方程由式(1)表示为

式中f(X) 为结构动力系统随时间t变化的一般非线性函数。

由ti(i ＝1，2，…，m) 时刻监测数据可得式(1)近似表达式，由式(2)表示为

假设式(1)为非线性多项式，设f(X) 由矩阵Q和相应的A构成，由式(3)表示为

式中Q为(n -1)× m阶应变速率矩阵，Q ＝；A为多项式相应系数矩阵，

在所建立的模型中，仅A未知，因此可采用多项式拟合最小二乘法，即用残差的加权平方和最小值的方法求解A。采用多项式的最小二乘曲线拟合，可求得系数ai(i ＝0，1，2，3) ，得到3 阶阶次动力学方程，由式(4)表示为

1.2 突变理论

突变理论是分析事物状态从一种状态到另一种状态跳跃变化的数学方法，突变理论包括7 种变换类型，尖点突变模型势函数[16]由式(5)表示为

式中x为系统状态变量；u、v为势函数的控制变量。

尖点突变模型势函数对系统状态变量x的一阶导数，由式(6)表示为

奇点满足方程由式(7)表示为

由平衡方程和奇点可建立尖点突变模型，如图1 所示。分叉集曲线即Δ ＝0 为平衡曲面的褶皱处在(u，v) 平面上的投影。当分叉集Δ ＞0 时，方程只有1 个实根，即系统状态变化是连续的，不会发生突变；当分叉集Δ ＝0 时，方程有3 个实根，此时系统处于临界稳定状态；当分叉集Δ ＜0 时，方程有3 个不相等的实根，系统状态跨越分叉集发生突变，出现失稳现象。

图1 尖点突变模型图

1.3 结构稳定性判据推导

式中bi(i ＝0，1，2，3，4) 为待定系数。

据此，通过判别式(8)可定义空间钢结构稳定性判定准则:Δ ＞0 为稳定状态；Δ ＝0 为临界状态；Δ ＜0 为失稳状态。

1.4 突变级数法

突变级数法是基于突变理论演化出来的一种综合评估方法，其计算步骤为:(1) 将结构系统分为若干指标；(2) 选取合适的突变系统类型通过分歧方程归一化公式定量计算指标突变级数；(3) 确定结构整体突变级数值[13]。

尖点突变模型可用于2 个指标的综合评估，通过联立V′(x) 和V″(x)，即式(6)和(7)消去x，计算出尖点突变模型的系统分叉集方程，由式(12)表示为

假设评估目标E分解为2 个指标，表示为E➝(xa，xb)。通过式(12)可解出尖点突变归一化公式，由式(13)表示为

式中a、b为E➝(xa，xb) 中的控制变量。

利用归一化公式进行综合评估计算突变级数值时需考虑非互补原则和互补原则。对于非互补型指标，即指标间不存在相关性，按大中取小取值为min{xa，xb} ；对于互补指标，即指标间存在相关性，按平均值法取值为。

1.5 主成分分析

监测系统布置大量的传感器，监测数据维数过多容易淹没有效特征数据。同时，采用突变级数法综合评估时，指标选取过多将会增加计算的复杂度和信息的冗余度。主成分分析法可以从相互关联的高维数据中提取有效特征，将高维相关变量转变为低维线性无关的变量，实现对数据的降维[17]。假设监测数据有n个样本、m个传感器，且第j个传感器对应第i个测量为yij，则可构造n × m维的矩阵Y，由式(14)表示为

采用Z-Score 对其标准化，标准化公式由式(15)表示为

计算标准化后数据的协方差矩阵R由式(16)表示为

式中rij(i，j ＝1，2，…，m) 为标准化指标间的相关系数，满足rij ＝rji。

求出监测数据协方差矩阵R特征值λi及对应单位正交特征向量，由式(17)表示为

式中ωi为特征值λi对应特征向量。

计算方差贡献率，由式(18)表示为

将各个主成分方差贡献率相加计算得到其累计贡献率，当m个主成分方差累积贡献率＞85%，说明提取特征可有效反映高维数据信息，则可得到主成分F，由式(19)表示为

式中Ω＝(ω1ω2…ωm)T为特征值对应特征向量。

通过主成分的提取不仅将原始具有相关性的监测数据转变为线性无关的特征数据，而且可以提取出与实际状态变量相近的结果，因此很适合提取分析结构健康监测数据。

2 工程实例

2.1 工程概况

潍坊北站屋盖为大跨度空间桁架结构，结构设计使用年限为100 a，安全等级为一级。抗震分区将屋盖结构分为4 个区域，东西向最长结构单元为194 m、外悬挑最大长度约为38.5 m。屋盖构件选用Q345B 钢材，强度设计值为305 MPa、弹性模量为210 GPa。为了保障结构安全运维，建立健康监测系统对关键杆件实时监测，并进行状态评估。其南站房的屋盖结构健康监测系统中光纤光栅应变传感器共布置19 支，布置位置如图2 所示。

图2 测点传感器布置图

2.2 稳定性分析

由于整体布置传感器数量较多，文章选取南站房屋盖结构健康监测系统2019 年5 月1 日—6 月30 日应变传感器监测数据分析研究，监测数据如图3 所示。在此期间，结构健康监测系统运行正常，无传感器损坏等故障，监测数据可反映实际结构监测指标参量。

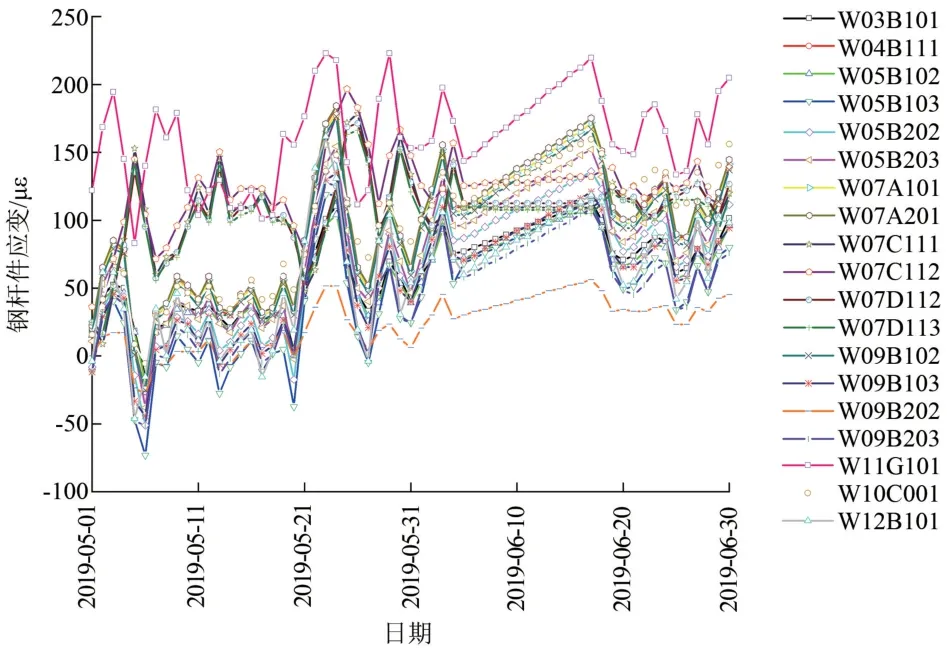
图3 屋盖应变监测值图

以测点W03B101 为例，监测数据按式(2)求得应变速率，测点W03B101 应变速率见表1。

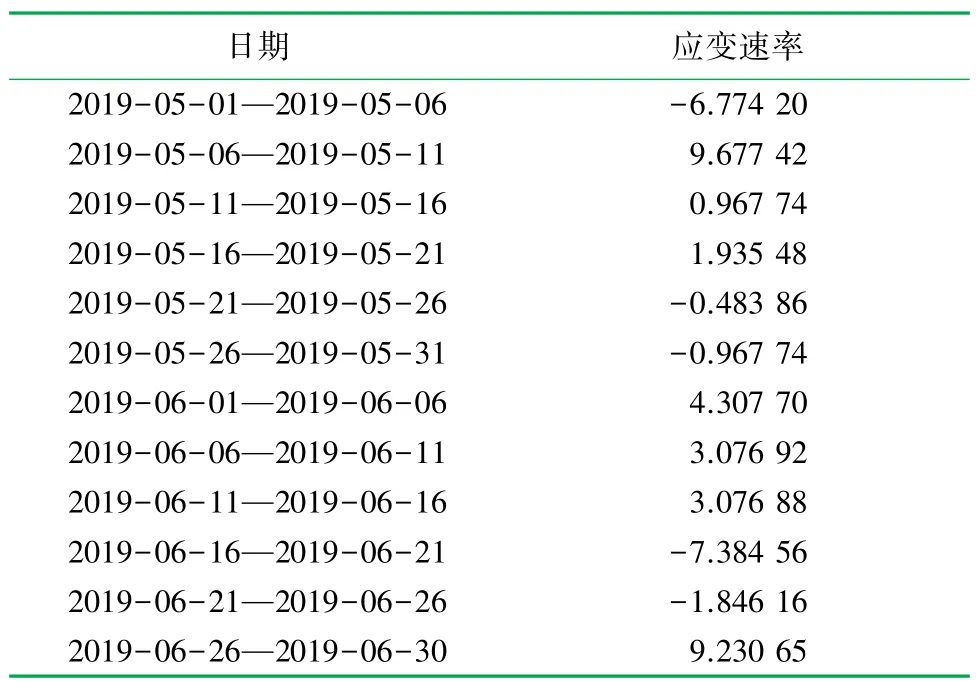
表1 测点W03B101 应变速率

将应变速率作为非线性动力学方程特解，按1.1节基础理论反演出动力学方程，由式(20)表示为

对式(20)积分，得到的算式由式(21)表示为

对式(21)进行Tschirnhaus 变换，得到的算式由式(22)表示为

式(23)为尖点突变模型标准形式，u＝-2.052 550、v＝3.174 264，则可得到判别式Δ ＝8u3＋27v2＝202.872 4，即Δ＞0，说明测点W03B101 位置处结构是稳定的。同理，可得其他测点判别结果，南站房屋盖结构测点处稳定性的计算结果见表2。

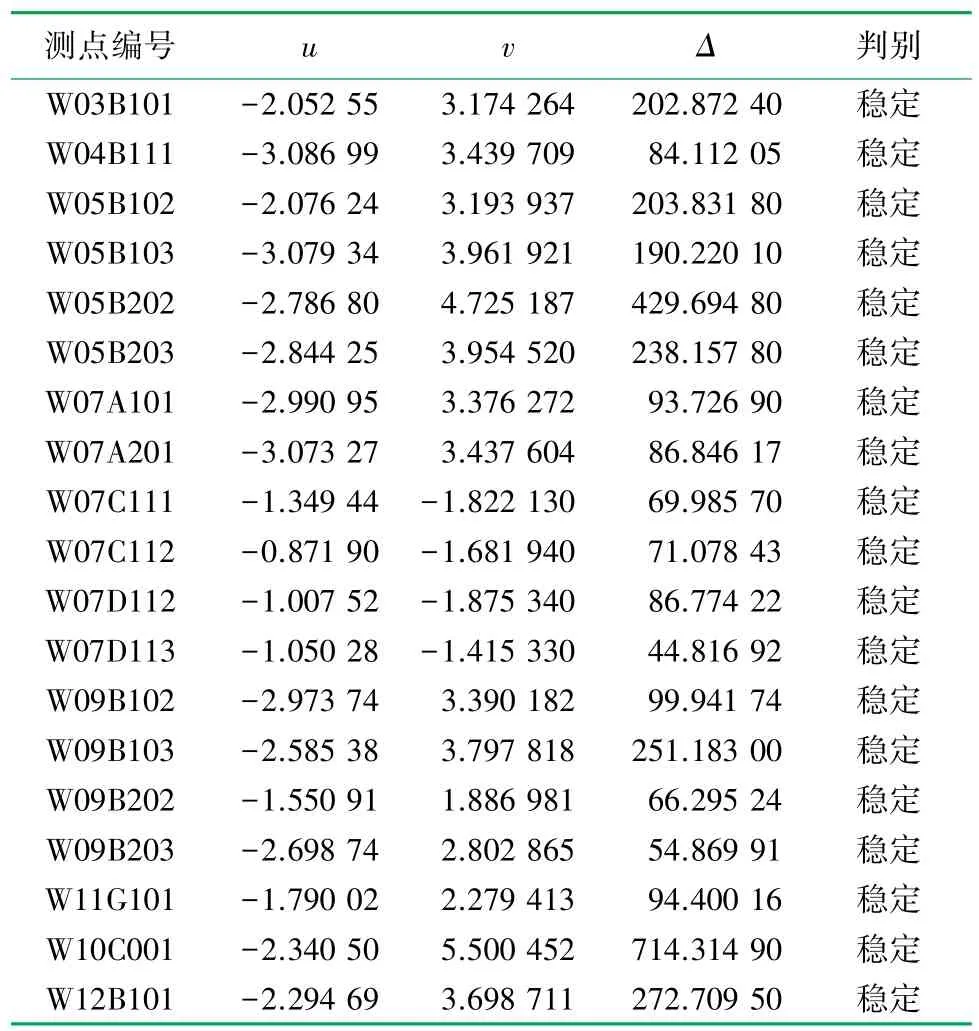
表2 南站房屋盖测点尖点突变模型势函数系数及判别表

根据尖点突变理论建立模型对空间结构屋盖监测结果进行分析，由表2 可知，各测点应变速率尖点突变模型的判别式Δ＞0，可以判断南站房屋盖结构所有应变测点处于稳定状态。同时，结构健康监测系统中各指标监测数据分析与数值研究均表明潍坊北站南站房的屋盖结构满足稳定性要求。为了说明方法的适用性，以文献[15]中凯威特型单层网壳结构分析验证。由上述方法可得到结构单元尖点突变模型标准形式:V(z)＝z4-19.425z2-8.16521z -158.448。其中，u＝-19.425、v＝-8.165 21，则可得到判别式Δ ＝8u3＋27v2＝-158.448，即Δ＜0，说明结构单元发生失稳。

2.3 综合评估

对空间结构综合评估时，因监测数据较多易淹没有效特征数据，因此采用主成分分析法降维并提取结构特征数据。根据式(15)～(18)提取主成分特征值及方差贡献率见表3。

表3 主成分特征值及方差贡献率表

由表3 可知，主成分F1和F2的贡献率分别为75.857%和20.533%，累计贡献率达96.390%。这说明F1、F2两个主成分可以反映出应变监测数据96.390%的信息量，提取信息较为充分，有效降低了信息维数。通过对监测数据分析可知，第一主成分F1反映了屋盖结构测点W03B101、 W04B111、W05B102、 W05B103、 W05B202、 W05B203、W07A101、 W07A201、 W07C111、 W07C112、W07D112、W07D113、W09B102、W09B103 的应变情况，第二主成分F2反映了屋盖结构测点W09B202、W09B203、W11G101、W10C001、W12B101 的应变情况，可以看出屋盖结构右半区域应变情况对屋盖结构整体稳定状态的影响占到75.857%，与有限元计算下的屋盖受力分析得出结果相符。F1、F2两个特征向量由式(24)和(25)表示为

式中y1～y19分别为不同测点应变监测数值，με。

在用式(13)评估之前，对指标进行标准化，由式(26)表示为

式中q1、q2、q3、q4为标准化区间值；d1、d2、d3为指标区间值，με。

依据GB 50017—2017《钢结构设计标准》[18]考虑Q345 钢理论屈服应变及结构构件实际受力性能，设定应变指标区间值和标准化区间见表4。

表4 指标区间值表

以2019 年6 月30 日监测数据为例，通过式(24) 和(25) 提取出主成分F1＝140.342、F2＝132.52，再通过式(26)对主成分数值标准化，由式(27)和(28)表示为

由于提取出两个主分量F1、F2满足尖点突变模型、突变级数法2 个指标的要求，运用尖点突变模型归一化公式(13)计算2 个指标突变级数值，由式(29)和(30)表示为

由于提取主成分向量F1、F2线性无关，因此依据非互补原则求取突变级数值，由式(31)表示为

即其突变级数值为0.927。同理，可求得其他时间突变级数值，由历史监测数据得到结构突变级数值较大且基本稳定，说明空间钢结构屋盖整体稳定性较好。

综上分析，得出空间钢结构屋盖稳定性分析和综合评估结果的一致性较好，尖点突变理论在空间结构稳定性分析和综合评估中具有适用性，同时验证了主成分分析在结构健康监测海量数据降维中具有有效性。应该指出，文章所提结构稳定性分析方法是广义上的稳定，即结构失稳的几何突变。该方法不仅适用于具有结构健康监测系统的结构稳定性评估，同时为既有建筑结构稳定性分析和综合评估提供了新思路。