基于SVM的电网物资价格预测模型研究

黄龙山

（福建榕能电业集团有限公司，福建 福州 350108）

当电网需要采购电力物资时，首先由计划部门确定采购的数目以及价格，然后电网公司会利用这个价格安排融资，并最终进行公开竞争招标。由于招标过程的时间较长，会导致招标价格与申报价格相差很大。这些差异增加了不必要的高额贷款利息和设备采购成本。为了规避这种情况，需要对电网物资价格进行预测，并且使预测价格尽量与实际招标价格一致，这样可以降低采购成本[1]。

当前背景常用预测方法有灰色理论、时间序列法以及贝叶斯理论等，在电力负荷预测、石油价格预测、铁矿石、有色金属价格预测以及农产品价格预测等多个领域中得到广泛应用。现有的研究大多是建立在价格为平稳序列的假设下进行的，这一假设仅适用于价格形成机理简单，影响因素单一的产品价格预测[2]。

但是电网物资价格受多种影响因素的共同作用，其价格形成机理十分复杂，因此电网物资价格表现为非平稳、非线性的时间序列[3]。传统预测方法不能满足电网物资的预测需求，经过对大量相关文献的分析，最终决定采用支持向量机方法来预测电网关键物资价格，并与BP 神经网络模型预测效果进行对比。

1 SVM 价格预测模型构建

使用皮尔逊系数评估特征与价格之间的相关性，并筛选出相关性较高的特征。将原材料价格和关键特征结合形成训练数据集。将训练数据集分为两个部分，分别为测试集和训练集，然后基于支持向量机算法和BP 神经网络算法分别对其进行预测。使用测试集来检查预测结果的准确性。最终通过预测效果评价指标来评估预测效果，评价指标选用均方误差（MSE）和校正相对系数（R2）[4]。

1.1 SVM 基本原理

支持向量机（SVM）[5-7]本质上是一种新颖的机器学习方法，它是基于统计学习理论和优化理论发展而来。常用于模式识别、分类和回归分析等领域。其重要之处在于维理论以及结构风险最小化原则，可用于解决线性和非线性分类问题。支持向量机的主要思想是找到最佳的超平面，将不同类型的数据点划分到不同的区域。总之，通过寻找模型复杂度和学习能力之间的最佳平衡点，支持向量机可以取得很好的效果。使用有限的样本信息来获得最好的推广能力。为了解决那些在低维空间中无法通过线性方式分开的数据样本，采用一个叫做非线性映射的方法，将这些样本映射到高维空间中。支持向量机具备简单的结构、较强的全局优化和泛化能力，能有效地解决高维和非线性问题。基本上，支持向量机就是通过间隔来确定置信风险的，同时通过参数来在经验风险和置信风险之间进行权衡。这样，它能够得出少数支持向量决定的最佳分类超平面，并且还具有稀疏性。支持向量机的模型类型为凸二次规划模型，不易陷入局部最优解的问题，具有非常强大的非线性处理能力。

1.2 建立SVM 模型

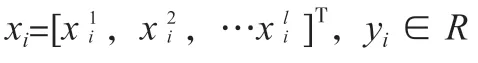
在高维特征空间中，可以建立一个线性回归函数：f（x）=ωΦ（x）+b。

其中，Φ（x）为非线性映射函数，定义ε线性不敏感损失函数。

在回归函数中，f（x）代表函数返回的预测值，而y为表示对应的实际值。

式中：C为惩罚因子，C越大表示对训练误差大于ε的样本惩罚越大，ε规定了回归函数的误差要求，ε越小表示回归函数的误差。

1.3 模型的求解

这里引入Laragange 函数，并将上式转换为对偶形式，转换如公式（2）所示。

可以通过设置最优解为α=[α1，α2，…αl]，则有公式（3）和公式（4）。

可以通过MATLAB 软件来对数据进行进一步分析和处理，结果会返回两个参数，第一个参数就是所得的预测值，第二个参数包括均方误差以及R2[8]，可以通过这2 个系数来确定预测值的精度，其计算如公式（5）所示。

2 模型实证分析

电力系统的关键物资比较多，选用某电力公司变压器物资的价格进行预测，并将预测价格与实际招标价格进行比较，检验该文所提的支持向量机模型价格预测结果的可靠性。

2.1 数据预处理

在该文中采集的数据包括缺失值、奇异值、字符型数据等，因此需要对这些数据进行预处理。对缺失值、奇异值而言，预处理方法是去掉奇异值变为缺失值，奇异值包括招标价格和申报价格的奇异值，如招标价格为 0、申报价格是实际价格的5 倍或更大等均为奇异值，然后使用中位数对缺失值进行填充，可以有效避免极端值对预测的影响。对字符型数据进行拆分、编码等，转化为数值型数据。

2.2 影响因素

影响变压器价格的因素有很多，例如安装方式、绝缘方式、中标单价以及额定容量等。部分因素对价格的影响并不是很大，为了避免关注过多的因素从而导致计算难度增大且可能产生不必要的干扰，该文决定仅考虑对价格影响程度较大的因素。

皮尔逊相关系数的作用是衡量两个影响因素之间的相关程度，其相关程度由两个影响因素的协方差和标准差的商表示。若通过计算得到两个影响因素的相关系数越接近于0，则说明这两个影响因素的相关程度就越低，反之，若得到的数越接近于1，则说明这两个影响因素的关联程度越大。皮尔逊相关系数的表达式如公式（6）所示。

式中：X，Y是2 个数据组，其中X（x1，x2，x3……），Y（y1，y2，y3……）；cov（X，Y）表示X，Y两组数据的协方差，用以表征X，Y两组数据彼此之间相互影响的程度，协方差绝对值越大，表示两者对彼此的影响越大，反之，越小。E表示均值，E（X）表示X组数据的均值，E（Y）表示Y组数据的均值。σX表示X组数据的样本标准差，σY表示Y组数据的样本标准差。

该文通过大量试验得出，当某一影响因素的皮尔逊相关系数达到0.35 时，该影响因素对预测价格的影响程度达到要求，因此根据相关经验，该研究设置3 个过滤常数，依次为0.35、0.37 和0.38，当某一影响因素与待预测价格之间的皮尔逊相关系数低于0.35 时，则将次影响因素过滤掉。然后对皮尔逊相关系数大于0.35 的影响因素继续重复上述操作，两两进行皮尔逊线性相关性的评估。

采用Pearson 相关系数法和行业专家的实际经验对影响变压器的多个因素进行分析，筛选出额定容量、铁芯材质、绝缘方式、安装方式和采购单价5 个主要因素来作为最终的影响因素。该文使用独热编码方法，将字符型数据转化为数值型数据。将表1 的样本数据转化为表2 的数值型数据，数据来自某电力公司，表1 和表2并未显示所有数据，仅列出了部分数据，以展示样本数据的转化。

表1 原始数据

表2 转换后的数据

2.3 支持向量机预测价格

由于变压器的3年数据并没有非常大，因此，为了保证预测的准确性，对所有数据进行训练，支持向量机采用默认的RBF 核函数，利用交叉验证方法确定最佳的惩罚因子c和RBF 核函数方差g参数，然后用这些参数来训练模型。其训练情况如图1所示。

图1 训练集情况

通过均方误差核决定系数的数值来看，整体的训练结果还是较为良好。为了得到变压器最终价格的预测情况，且为了不失一般性，采用了四组支持向量机模型预测，每组通过随机选择10 个数据进行预测。具体情况如图2所示。

图2 支持向量机预测情况

2.4 神经网络预测价格

数据预处理的方式同支持向量机模型数据预处理方式，数据每组为7 维，第一维到第六维为变压器价格的影响因数，第七维是变压器的中标单价。由于数据量并不多且工作量不大，可以采用对整体数据进行训练，也可避免数据的分布不均衡对预测产生较大的影响。

对BP 神经网络的预测[9-10]，采取与支持向量机相同的预测方式。为了得到变压器最终价格的预测情况，且为了不失一般性，采用了四组BP 神经网络模型预测，每组通过随机选择10 个数据进行预测。具体情况如图3所示。

图3 BP 神经网络预测情况

2.5 对比情况

通过表3 的直观对比，支持向量机价格预测模型的均方误差均值为0.0064634，小于BP 神经网络价格预测模型的0.01130202，支持向量机预测模型的校正系数均值为0.9462825，大于BP 神经网络预测模型的0.9124275，很明显，在变压器的价格预测中，还是支持向量机的预测精度要更精确一些，但在整体上误差并不是很大。此外在计算过程中发现支持向量机模型的速度比BP 神经网络预测模型更快。

表3 预测误差对比情况

3 结论

正确预测电网物资的价格对电网企业来说非常重要，因为预测价格的高低会直接影响到物资成本和损失。该文选取电网关键物资变压器作为预测对象，通过数据预处理来筛选出有用数据，并利用历史数据中的皮尔逊系数确定了影响电网物资价格的关键特征，筛选出额定容量、铁芯材质、绝缘方式、安装方式和采购单价5 个主要因素。分别采用BP 神经网络与SVM 两种模型，利用预测评价指标均方误差和校正相对系数来评估预测结果，对同一目标的不同预测模型的结果进行比较，提高变压器价格预测时结果的准确性，减少误差。得到了支持向量机预测模型、BP神经网络预测模型的均方误差分别为0.65%、1.13%，校正相对系数分别为0.9462825 与0.9124275，结果表明支持向量机模型的预测精度更好，可获得较为理想的结果。此外，在预测过程中支持向量机模型的预测速度比BP 神经网络模型快。该研究结果可为电网企业的物资价格预测提供参考。