基于无人机集群的森林防火监测技术研究

刘金荣

（吉林省通化县林业局，吉林 通化 134100）

随着科学技术的发展，我国无人机作为森林灾害监测和救援的基本平台已经得到广泛重视和应用[1]。我国专家和学者对无人机用于消防领域的现状及可行性进行论述。在森林火灾背景下，无人机由于动力、续航能力的限制，单架无人机对监测面积较大的森林防火任务难以胜任。针对这一情况，采取多无人机配合、以无人机集群完成火灾监测成为一种合理的方案。无人机集群中含有多个无人机，各个无人机之间相互协调、协同配合，提升了覆盖范围和复杂任务的执行能力，是无人机技术未来的重要发展方向[2]。无人机集群承担的任务多为多目标、多参数、多网点的复杂任务，为了完成总体任务，各个无人机所承担的任务范围、任务数量就成为关键，从而推动了无人机集群任务分配问题成为领域内的研究重点[3]。无人机集群任务分配的核心目标是在确保总体任务完成的前提下，高效使用每个无人机，即总体任务在各个无人机之间分配的均衡性。该文以森林防火的监测任务分配为背景，致力于无人机集群的分配方法和试验研究。

1 无人机集群的任务调度方法

1.1 粒子群算法

对大面积的森林防火监测任务来说，采用多个无人机构成的无人机集群具有更好的针对性，也可以胜任这种大面积、高复杂性的防火监测。对应于无人机集群，将集群内每架无人机看作一个个体，无人机集群的任务调度就变成了多个体均衡调度问题。适用于这一问题的求解方法包括多属性决策方法、遗传算法、神经网络算法、粒子群算法。

粒子群算法以每个粒子对应一个个体，全部粒子的集合就对应于整个集群。粒子群算法通过设定初始条件、限制条件和目标约束，致力于在一个特定适应度函数的优化下，找到整个集群的最佳位置，并形成持续的动态演化。根据适应度函数的优化和各种优化控制条件，粒子群会调整每个粒子的位置、速度等参数，同时兼顾各个粒子之间的均衡和协调，从而使整个粒子群达到最佳状态。

在无人机集群监测森林状态的过程中，每个无人机个体就对应一个粒子，其位置的表征如公式（1）所示。式中：x为粒子群中一个粒子即无人机个体的位置；p为粒子群中一个粒子即无人机个体的初始位置参照；L为位置变化调整范围系数；u为一个随机数，其取值范围是（0，1）。

对无人机集群中的每个个体，其不考虑其他粒子只考虑自身情况下，在目标约束下不断对位置进行优化，可以得到的局部最佳位置，如公式（2）所示。

式中：xi（t）为第i个时刻粒子群中一个粒子即无人机个体的位置；pi（t）为第t个时刻刻粒子群中一个粒子即无人机个体的局部最佳位置；pi（t-1）为第t-1 个时刻刻粒子群中一个粒子即无人机个体的局部最佳位置。

如果综合考虑集群内全部粒子的情况，得到每个粒子在集群内的全局最佳位置，如公式（3）所示。

式中：G（t）为整个粒子群的全局最佳位置；pg（t）为第i个时刻粒子群中一个粒子即无人机个体的位置；g（t）为第t个时刻刻粒子群中一个粒子即无人机个体的全部最佳位置；g（t-1）为第t-1 个时刻刻粒子群中一个粒子即无人机个体的全部最佳位置。

综合局部最佳位置和全局最佳位置的联合考虑，可以得到每个粒子个体的位置信息更新机制。

式中：xid（t）为第id个时刻粒子群中一个粒子即无人机个体的位置；pid为第id个时刻粒子群中一个粒子即无人机个体的位置；Lid为第id个时刻位置变化调整范围系数，uid为第id个时刻的随机数。

1.2 粒子群算法的实施步骤

粒子群算法在无人机集群森林防火监测任务分配时，每个无人机对应一个粒子群中的粒子，预期完成的任务为粒子群算法的优化目标，任务位置为粒子群算法的目标位置，算法应保证任务全部完成且每个无人机得到最大效率地使用，尤其要避免个别无人机任务负荷过重而个别无人机无任务的情况出现。根据这些要求以及粒子群算法的实现原理，设计无人机集群森林防火监测任务分配算法的流程：第一，根据任务要求、任务位置、无人机位置，对粒子群进行参数配置和初始化。第二，根据任务要求、优化目标构建适应度函数，并完成粒子群的适应度计算。第三，计算粒子的局部最佳位置和整个粒子群的全局最佳位置。第四，根据预设的更新机制，更新粒子的位置。第五，根据粒子的最新位置，更新每个粒子的局部最佳位置和整个粒子群的全局最佳位置。第六，判断此时的迭代误差是否小于预设，如果小于，就输出当前粒子群全局最佳位置。如果迭代误差大于预设，返回到第四步，不断重复第四、第五步，直到迭代误差小于预设。

上述算法的输出结果，整个粒子群的最佳位置对应配置给无人机集群，每个量子粒子的位置更新轨迹即成为无人机个体的规划路径。

2 仿真试验与结果分析

2.1 试验条件配置

为了验证该文提出的粒子群算法对无人机集群森林防火任务分配的有效性进行试验。在试验过程中，无人机集群配置了5 个无人机，其对应编号和坐标见表1。

表1 无人机编号和坐标配置

从表1 中可以看出，第一个无人机的初始位置在（36，13，26）的三维空间位置上，第二个无人机的初始位置在（21，35，43）的三维空间位置上，第三个无人机的初始位置在（15，28，28）的三维空间位置上，第四个无人机的初始位置在（28，49，25）的三维空间位置上，第五个无人机的初始位置在（35，31，20）的三维空间位置上。

试验中，配置了8 个任务目标点，其对应编号和坐标见表2。

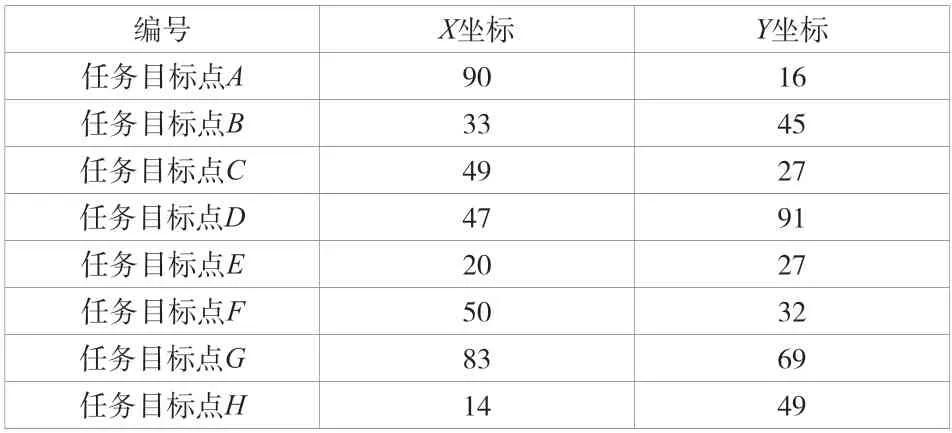
表2 任务目标点编号和坐标配置

从表2 中可以看出，第A个任务目标点在（90，16）的二维平面位置上，第B个任务目标点在（33，45）的二维平面位置上，第C个任务目标点在（49，27）的二维平面位置上，第D个任务目标点在（47，91）的二维平面位置上，第E个任务目标点在（20，27）的二维平面位置上，第F个任务目标点在（50，32）的二维平面位置上，第G个任务目标点在（83，69）的二维平面位置上，第H个任务目标点在（14，49）的二维平面位置上。

无人机集群执行的任务分为3 类，分别是第一周期监测、第二周期监测、第三周期，每个任务目标点上述三种任务的目标价值和总体价值，配置见表3。

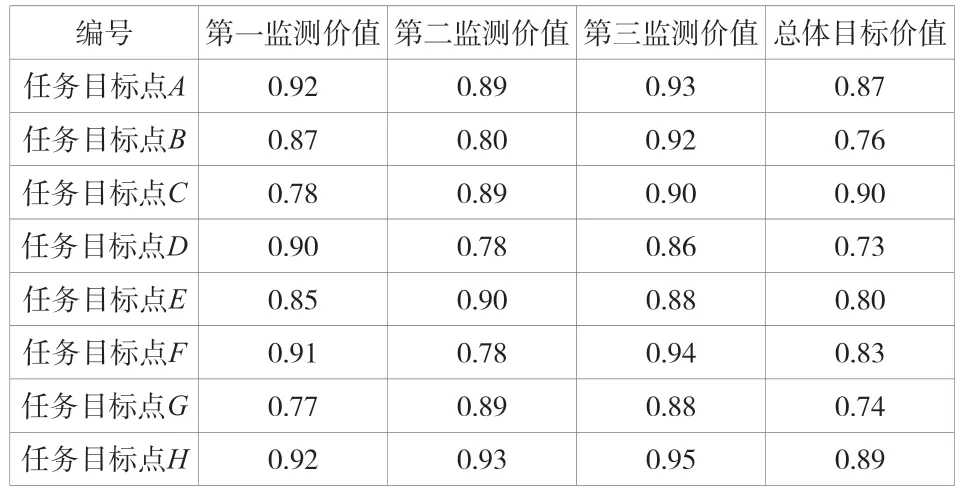
表3 任务目标点的三类任务目标价值和总体目标价值

从表1～表3 可以看出，无人机集群中每个无人机给出了空中三维坐标信息，而每个任务目标点给出的是平面地图的二维坐标信息，各个任务目标点的四类目标价值，是任务分配算法的优化目标。试验中，为了与该文提出的粒子群算法形成对比，还选择了遗传算法、传统粒子群算法，作为无人机集群任务分配试验中的参照方法。接下来，将分别进行三类任务的分配试验。

2.2 试验结果

首先，比较该文算法、遗传算法、粒子群算法在完成无人机集群监测任务分配时的适应度收敛曲线，结果如图1所示。

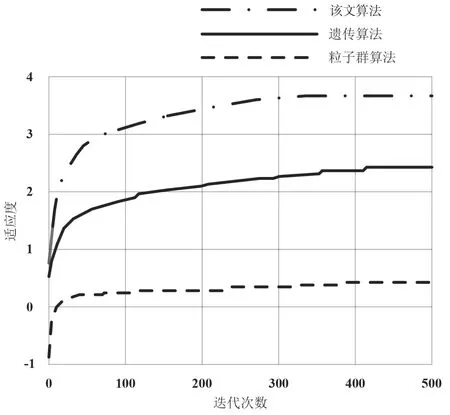
图1 三类算法的监测任务分配收敛曲线对比

从图1 中的结果可以看出，在无人机集群完成监测任务分配的过程中，该文算法的适应度达成收敛的速度最快，并且收敛时适应度值更高。传统粒子群算法、遗传算法的收敛速度都滞后于该文算法，并且收敛时的适应度较低。

进一步比较3 种算法完成的无人机集群侦察任务分配结果，如图2～图4所示。

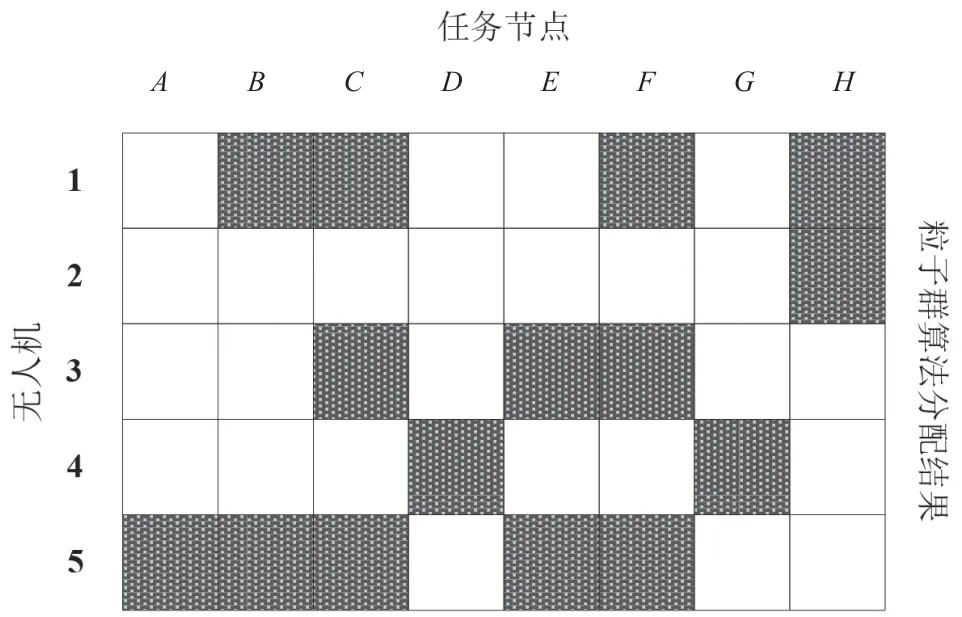
图2 传统粒子群算法分配结果

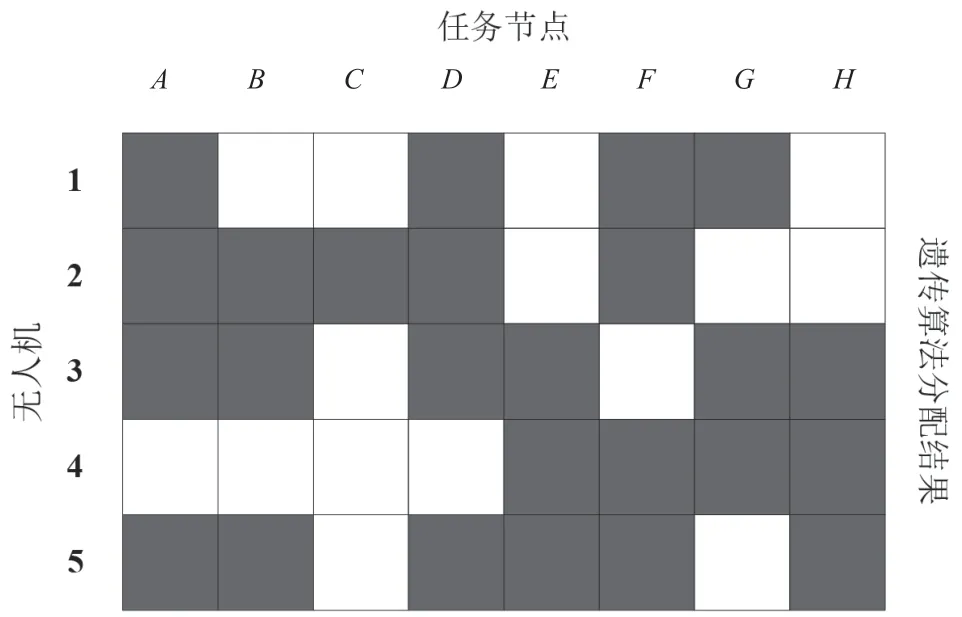
图3 遗传算法分配结果

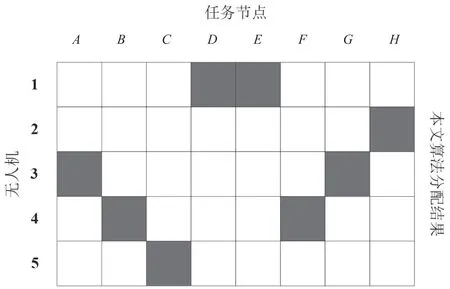
图4 该文算法分配结果

3 结论

从图2～图4 的对比结果可以看出，经过该文提出的粒子群算法完成的无人机集群监测任务分配结果，8 个任务目标点比较均衡地配置给了5 个无人机，1 号无人机负责D、E的监测，2 号无人机负责H的监测，3 号无人机负责A、G的监测，4 号无人机负责B、F的监测，5 号无人机负责C的监测，每个无人机都得到了接近最大效用的使用，无人机资源没有造成浪费和任务过载。粒子群算法得到的监测任务分配结果，各无人机任务分配不均衡，2号无人机任务过少，而1 号无人机和5 号无人机的任务过重。同时，传统粒子群算法得到的监测任务分配结果，造成了多个无人机任务过载和任务目标点重复侦察的问题。遗传算法也出现了类似问题，并且任务过载和任务重复执行的程度更严重。

无人机已经在很多领域中得到了广泛应用，无人机集群也日益成为复杂问题的合理解决方案。森林防火监测面积大、监测情况复杂，运用单一无人机很难达到预期的理想效果，采用无人机集群完成森林防火监测，是一种非常合理的手段。该文对传统粒子群算法进行进一步改进，从局部最佳位置、全局最佳位置完成粒子更新公式设计。在此基础上，以传统粒子群算法和遗传算法为对比方法，与该文提出的改进粒子群算法进行无人机集群监测任务分配的对比试验，试验结果显示：该文方法获得的无人机集群监测任务分配结果更合理，没有无人机出现过载，每个无人机都达到了最大效率。