基于SEA的常规导弹封锁机场跑道作战效能分析与应用
2023-10-14李新其李红霞邱艳粉
李新其,李红霞,邱艳粉
(1.火箭军工程大学 初级指挥系,陕西 西安 710025;2.西北政法大学 军民融合发展研究院,陕西 西安 710025;3.中国人民解放军96723部队,广西 柳州 545000)
作战效能的分析与评价是军事运筹学中的一项基础研究内容[1]。尽管在军事运筹中给出了适用于一般情况下的作战效能分析方法与步骤,但传统的武器系统效能分析的目的主要还是为武器系统研制、规划及配置提供一个可进行优劣对比的基本依据[2-3],故其主要应用于装备的发展论证上。从作战使用的角度来说,武器定型并装备部队后再进行武器性能的比较已无必要,因为武器使用者关注的是使用列装武器完成指定作战任务的把握程度。此时,作战效能研究侧重于分析不同作战环境下影响武器作战效能的因素及提高作战效能的途径[4-5]。
就常规导弹封锁机场跑道而言,攻方关心的问题通常有:①在明确系统结构、环境、使命,并给出各类原始参数信息后,如何对武器完成作战任务的把握程度做出评估;②在给定效能指标条件下,如何求取待定的参数组(主要指弹量计算问题);③如何对各种打击方案的优劣进行评估,从而为导弹武器火力运用提供可靠的理论依据和切实可行的辅助决策信息。
从上述问题出发,将常规导弹作战效能分析理论的基本任务归纳为4个方面:效能(任务)评估、弹量计算、方案选优和效费比分析。拟结合实例,详细阐述如何运用系统效能分析(system effectiveness analysis,SEA)方法解决这四类问题。
1 封锁把握程度评估
评估武器系统完成任务的把握程度,是作战效能分析的首要问题,又称其为作战效能分析的正问题。
例1评估单独使用某型侵彻子母弹封锁机场的作战效能。
导弹武器参数做出如下假定:子弹瞄准精度δCEP=200 m,装填子弹数100枚,子弹群抛撒可在100~300 m之间,发射成功率、飞行成功率、子弹成爆率均为100%。
其他环境原始参数假设如下:守方的反导系统都被假定为爱国者3,对攻方导弹的拦截概率为Pxy,反导系统可同时拦截的来袭导弹枚数的最大值为3枚;子弹对跑道的平均毁伤面积为Sh,同时抢修弹坑数量为Mmax,服从(αϖ,βϖ)间的均匀分布。跑道长3 658 m,宽45 m;最小起降窗口长度Lx_min=800 m,宽度Ly_min=20 m;
抢修参数:判定跑道损毁情况时间tdm=10 min,确定应急跑道抢修方案时间tpl=20 min。
作战任务要求:以80%的把握封锁机场90 min。
现按如表1所示的5个方案选取并分配弹量,试评估该型号武器完成任务的把握程度。表1中位置原点为机场跑道中心。按照文献[6]给出的模型,经计算得到表2的结果。可知在抛撒半径Rth为120~290 m时,5个方案都满足任务要求。
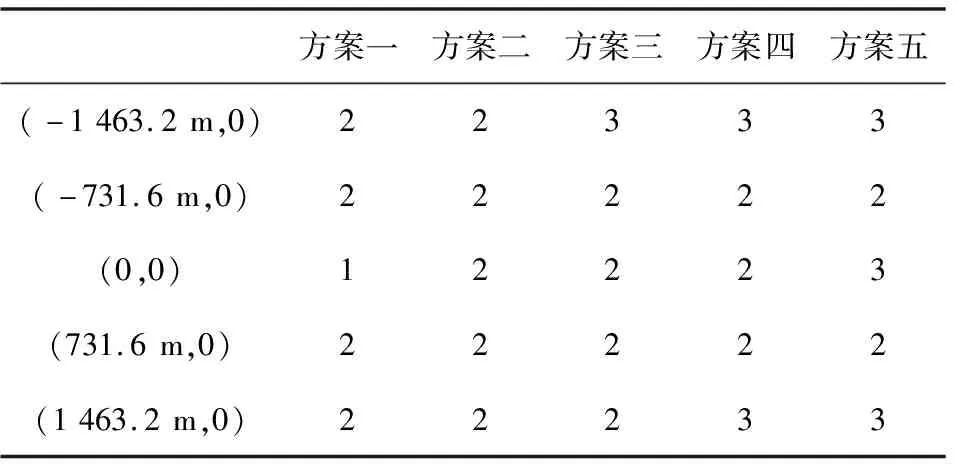
表1 弹量分配方案表Table 1 Missile number and its aim point

表2 子母弹封锁机场把握程度Table 2 Mastery degree of cluster bomb blocking airport %
例2评估组合使用某型侵彻子母弹和延时子母弹封锁跑道的作战效能。
侵彻子母弹武器参数同上,延时子母弹武器参数:精度δCEP=200 m;装填子弹数100枚;子弹群抛撒半径Rth在100~300 m之间选择;瞄准点选取及弹量分配方案同上。
作战任务要求:以80%的把握程度封锁机场120 min。经计算,不同抛撒半径、弹量分配方案下延时子母弹封锁机场把握程度计算结果如表3所示。可知在抛撒半径为140~290 m时,5个方案都满足任务要求,且方案五的封锁把握程度几乎都是最高的,不同方案中,抛撒半径在200 m左右最佳。

表3 延时子母弹封锁机场把握程度Table 3 Mastery degree of delayed cluster bomb blocking airport %
2 武器数量计算
耗弹量的计算是指在给定武器型号和作战任务要求的情况下,计算完成该任务所需的武器数量,这其实是作战效能分析的反问题,需应用作战效能分析理论求出给定效能指标条件下的待定参数组。
对于单波次打击方案而言,耗弹量的计算问题相对简单,只需在瞄准点上逐枚增加发射弹量,计算并比较效能值,直到满足规定的要求;但对于多波次打击,或需要使用不同类型导弹武器组合打击的情况,耗弹量的计算问题则复杂得多。
首先,定义封锁强度为机场跑道遭受导弹打击后,机场起降能力受损的程度。封锁强度越大,起降能力越低。封锁强度与落入跑道的子弹密集度、弹坑的大小及分布的均匀程度有关。由于跑道失效率φDPR能很好地体现落入跑道中子弹密度和均匀度与跑道失效时间的关系,进而表征跑道起降能力受损的程度,φDPR值越大,跑道受损越严重,说明封锁强度越大。
封锁强度量化的原则:
①封锁强度是随时间的推进不断减少的函数,取值范围在[0,1]之间;
②没有开始修复弹坑时,封锁强度等于跑道失效率φDPR[7-8],出现最小起降窗口时,封锁强度为0。
故封锁强度的函数形式为
(1)
式中:tf为跑道失效时间。
机场所担负的作战任务不能仅依靠少数架次飞机完成,因此,即使在某个较小的时间段内,经过跑道抢修分队的努力,跑道出现了最小起降窗口,使得少数架次的飞机得以起降,但这对于整个战役进程并不会发生大的改变。因此,用跑道失效时间和封锁把握程度同时满足任务要求作为衡量完成任务的标准,与机场封锁作战的实际情况不相符。
为此,定义封锁量为封锁强度在封锁时间内的积分(或封锁强度的时间延续),将其作为常规导弹封锁跑道的任务量指标,用于衡量完成任务的程度。封锁量W的函数形式为
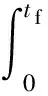
(2)
文献[6]中由于φDPR近似服从Beta分布,其分布密度函数为
(3)
tf服从正态分布,其密度函数为f2(tf),故根据卷积公式,可推知W的概率密度函数为
(4)

如果作战任务的封锁时间为tk,封锁强度为φDPR,k,则封锁量为Wk=tkφDPR,k,完成此任务量的概率即为完成任务的把握程度:

(5)
当把握程度无法满足要求的程度时,则增加弹量,用迭代法求出最优解。
例3单波次打击中的弹量计算。
根据例1所给出的导弹武器参数及目标参数,计算各型号武器以0.8的封锁强度,封锁机场跑道时间分别为60 min,75 min,90 min,完成任务的把握程度都为80%时,计算所需的弹量及最佳抛撒半径。
经计算,以80%的把握程度封锁例1机场目标60 min,75 min,90 min,所需弹量不得少于9,10,11枚,最佳抛撒半径为210~220 m。通过大量仿真计算得到封锁量与封锁把握程度的曲线,如图1所示。由图1可知,当成爆弹量达到12枚以后,封锁把握程度增幅有限。
由图8可知,酵母菌在模拟酒中的产气量随SO2质量浓度升高而降低,其中有氧环境活化所得酵母对SO2的耐受性显著高于厌氧环境活化所得酵母,但后者与普通方式活化所得酵母相比差异不显著。此外,有氧条件时,随活化培养液中碳源含量和氮源含量的增加,活化酵母菌对SO2的耐受性也随之提高,部分处理组差异显著。
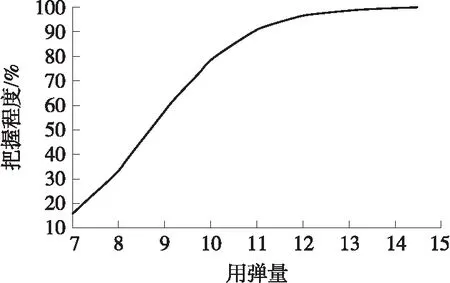
图1 某型侵彻子母弹不同用弹量与把握程度的曲线图Fig.1 Curve diagram of different amount of ammunition and grasping degree of a certain type of penetrating submunition
例4单波次多型号导弹武器混合打击中的弹型弹量计算。
在对机场的火力打击中,可同时使用某种轻型子母弹和中型子母弹打击机场跑道。在总用弹量为10枚,总封锁时间不低于90 min,封锁强度不低于0.8的前提下,以轻型子母弹和中型子母弹对例1中的机场跑道进行混合打击,计算最优方案。
轻型子母弹A导弹武器参数:精度δCEP=200 m;装填子弹数200枚;子弹群抛撒半径在100~300 m之间,每枚子弹的封锁时间为30 min。中型子母弹B导弹武器参数:精度δCEP=200 m;装填子弹数100枚;子弹群抛撒半径在100~300 m之间,每枚子弹的封锁时间为45 min。经计算,得到不同弹型弹量下的计算结果,如表4所示。
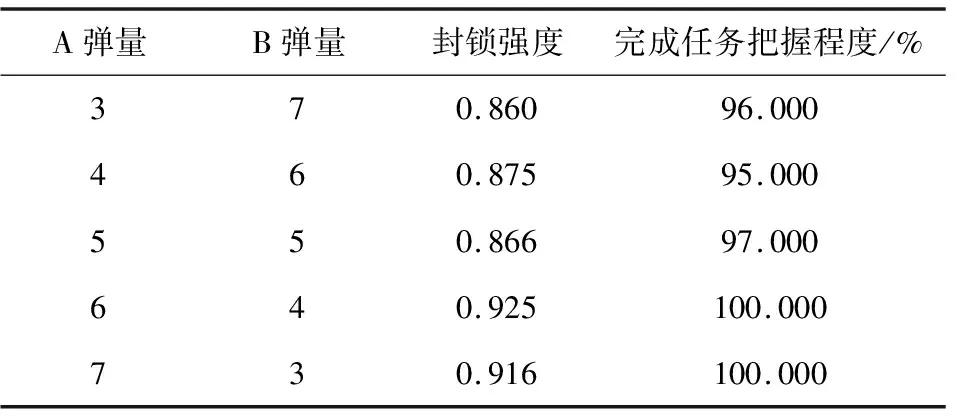
表4 不同弹型弹量组合下的计算结果表Table 4 Calculation results under different combination condition
例5多波次打击中的弹量计算。
当封锁机场跑道的作战要求封锁时限较长,而单波次打击无法满足封锁时间要求,需要进行多波次导弹打击。令第j波次打击时,封锁量为Wj,在作战要求封锁时限为tk的时间段内,其总的封锁量为Ws=∑Wj。Ws的分布密度可由各封锁量Wj推导而出,令fWs(Ws)。如果要求的封锁时间为tk,封锁强度为φDPR,k,完成任务的把握程度为Pk,则封锁量为Wk=tkφDPR,k,根据各波次封锁量的分布密度,可计算出相应弹量下完成此任务量的把握程度,即:

(6)
改变各波次弹量,当E≥Pk时,即达到规定的封锁任务要求。
在某次对机场火力打击中,拟使用某种轻型子母弹和中型子母弹,进行两波次火力打击。要求:前一波次的封锁强度达到0.8,后一波次的封锁强度不低于0.65,总封锁时间不低于180 min,试计算以80%的把握程度完成此任务的弹型弹量分配方案。
为此,制定2种打击方案:方案Ⅰ是以轻型子母弹A导弹第一波次先打,中型子母弹B导弹第二波次后打;方案Ⅱ是中型子母弹B导弹为第一波次,轻型子母弹A导弹为第二波次。根据模型计算得到表5和表6所示结果。表中,在计算2个波次各自的封锁强度时,置信概率都取为0.8。由结果可知方案Ⅰ满足任务要求。
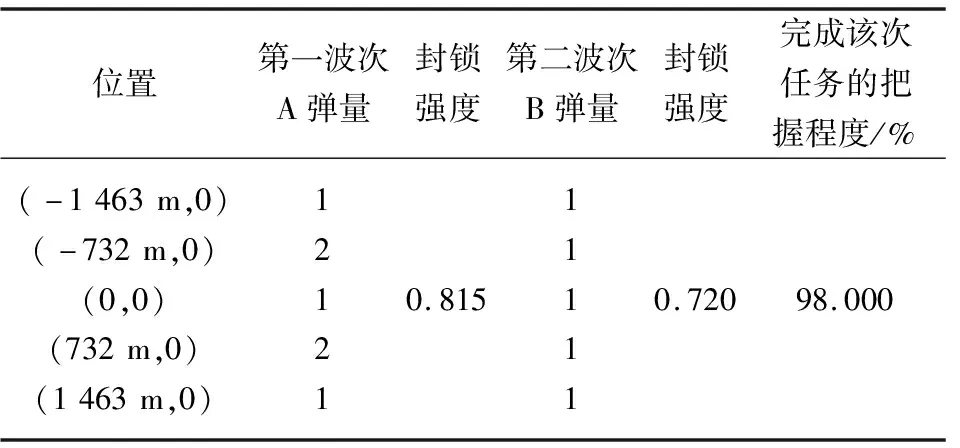
表5 方案Ⅰ弹量计算结果表Table 5 Calculation results of planⅠ
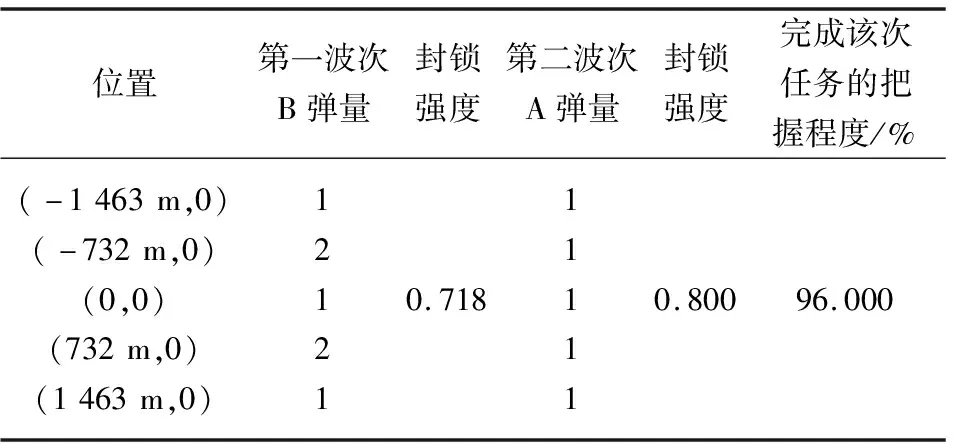
表6 方案Ⅱ弹量计算结果表Table 6 Calculation results of plan Ⅱ
3 武器系统效费分析
针对不同导弹武器系统进行效费分析时,统一选取封锁量作为效能指标。封锁量的分布密度及封锁量的计算方法参考文献[6]。假设使用XY型武器封锁机场,在把握程度不低于0.8的前提下,完成封锁跑道时间为ts,XY,封锁强度不低于φDPR,XY的作战任务,需要弹量NXY枚。则该型号导弹的效费比计算式为
(7)
式中:CXY为XY型武器单价。
例6几种常规导弹武器的效费比分析。
假设轻型子母弹单价1 500万元,中型子母弹1 800万元,各型号导弹使用件数、作战效能与总体费用情况如表7所示。

表7 各导弹武器系统作战效能与总体费用情况表Table 7 Effectiveness and total price of different missile systems
总体比较,方案Ⅰ的效费比与方案Ⅱ的比值约为1.414 3;相对而言,方案Ⅰ的效费比较方案Ⅱ要高,是更为合理的作战方案。
4 作战方预案评估
运用作战效能分析理论,可对各种火力打击方预案进行评估,从中选择作战效能最佳的方案。
例7仍以例1中的目标为例,使用中型子母弹武器对其进行打击,试对不同波次打击方案进行评估。
①单波次打击方案,发射13枚弹。
②双波次打击方案,每波次间隔时间为15 min,发射弹量分别为8和5。
③三波次打击方案,间隔时间为10 min,发射弹量分别为5,5,3。
④三波次方案,间隔时间为5 min,发射弹量分别为5,4,4。
根据本文的效能分析模型,计算得到方案①的封锁量为350.190 1;方案②的封锁量为381.463 2;方案③的封锁量为429.959 1;方案④的封锁量为369.511 1。可知在相同弹量情况下,方案③的作战效能最佳,应为最优打击方案。
5 结束语
本文根据常规导弹攻击机场跑道作战使用特点,运用SEA效能分析理论,对常规导弹封锁机场作战中的耗弹量、打击效果评估、火力方案筹划选优及武器系统效费比问题进行了定量分析。构建了导弹武器封锁机场跑道作战效能仿真的概念,验证了基于SEA的作战效能分析模型。本文工作可为作战效能分析评估提供理论基础。
