考虑润滑油齿面摩擦特性的齿轮啮合效率计算及优化分析
2023-10-14胡明用胡云波朱美玲
胡明用,胡云波,朱美玲
(湖南南方宇航高精传动有限公司,湖南株洲 412000)
0 引言
齿轮传动功率损失中,滑动摩擦损失和滚动摩擦损失组成的齿轮啮合功率损失占主要部分[1]。陈辛波等[2]提出了载荷均匀分布于接触线上,并采用了简化的齿间载荷分配系数的方法。王成等[3]提出一种通过人字齿轮副轮齿接触的分析方法,获得摩擦损耗功率。Xu Hai[4]建立了载荷分配模型,获得精确的齿面载荷分布情况,考虑了齿面粗糙度对摩擦因数的影响,实验数据表明,采用该模型计算的摩擦因数与实验值更为接近。Li Sheng等[5]分析了基于弹流润滑理论的斜齿轮啮合效率模型。Xu H.[6]对斜齿轮功率损失的计算有一定研究,但对斜齿轮设计参数与啮合效率之间的关系未做研究。
但这些研究并未考虑不同工作压力和温度变量下的润滑油对齿面摩擦特性的影响,进而去研究对齿轮啮合效率的影响。开展考虑润滑油的齿面摩擦特性的齿轮啮合效率计算方法研究,分析润滑油对啮合摩擦的影响,进而分析对齿轮啮合效率的影响规律,该啮合效率优化方案对整机设计具有重要意义。
1 齿轮啮合功率损耗及效率
1.1 齿轮啮合功率损耗
AGMA ISO 14179-1标准[7]给出了齿轮啮合功率损耗计算方法。
如果切向节线速度V为(2,25]m/s时,载荷强度K在(1.4,14]N/mm2范围内,啮合摩擦因数可表示为
式中,υ为润滑油运动黏度。
齿轮的啮合功率损耗为
式中:T1为小齿轮的转矩,n1为小齿轮的转速,β为螺旋角,M为啮合机械效益。
1.2 齿轮啮合效率
齿轮的啮合效率为
式中,P0为输入功率。
2 温度和压力对啮合效率的影响
2.1 温度对啮合效率的影响
流体黏度随温度变化的Walther公式[8]为
式中:T为润滑油的绝对温度,a、b、c为常数。
本文结合文献中润滑油的实测数据,来拟合公式(4),得到温度与润滑油运动黏度的关系。发动机油 5W -30 和5W-40 运动黏度的实测结果[9]如表1所示。

表1 发动机油5W-30和5W-40运动黏度的实测结果
4109 号和4050 号航空润滑油运动黏度的试验结果[10]如表2所示。
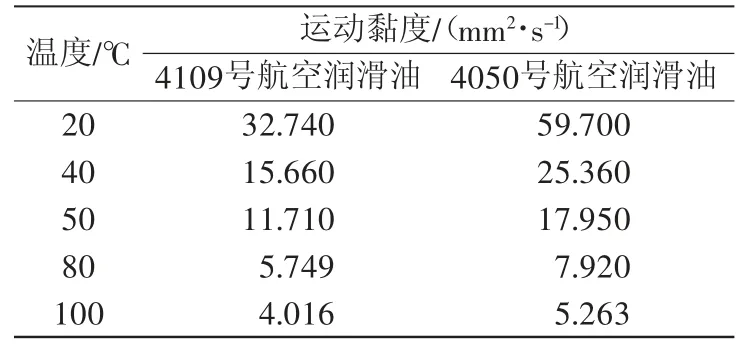
表2 4109号和4050号航空润滑油运动黏度的试验结果
SC30 汽油机润滑油和20号航空润滑油运动黏度的试验结果[11]如表3所示。
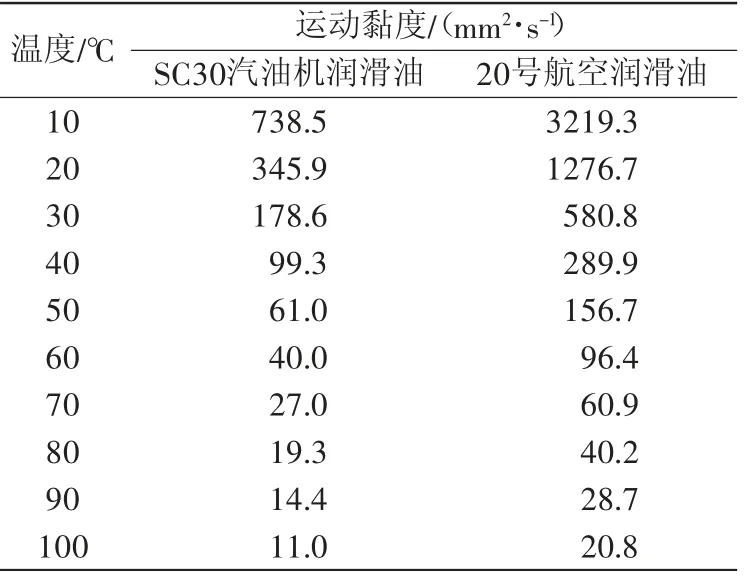
表3 SC30汽油机润滑油和20号航空润滑油运动黏度的试验结果
根据润滑油的运动黏度试验结果,可以拟合润滑油的 Walther公式,如图1所示。
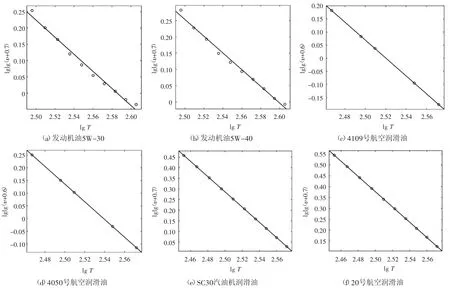
图1 润滑油的Walther公式拟合直线
润滑油的拟合Walther公式如表4所示。

表4 润滑油的拟合Walther公式
根据润滑油 的 拟 合Walther公式得到润滑油在温度为40~150 ℃下的运动黏度,如表5所示。
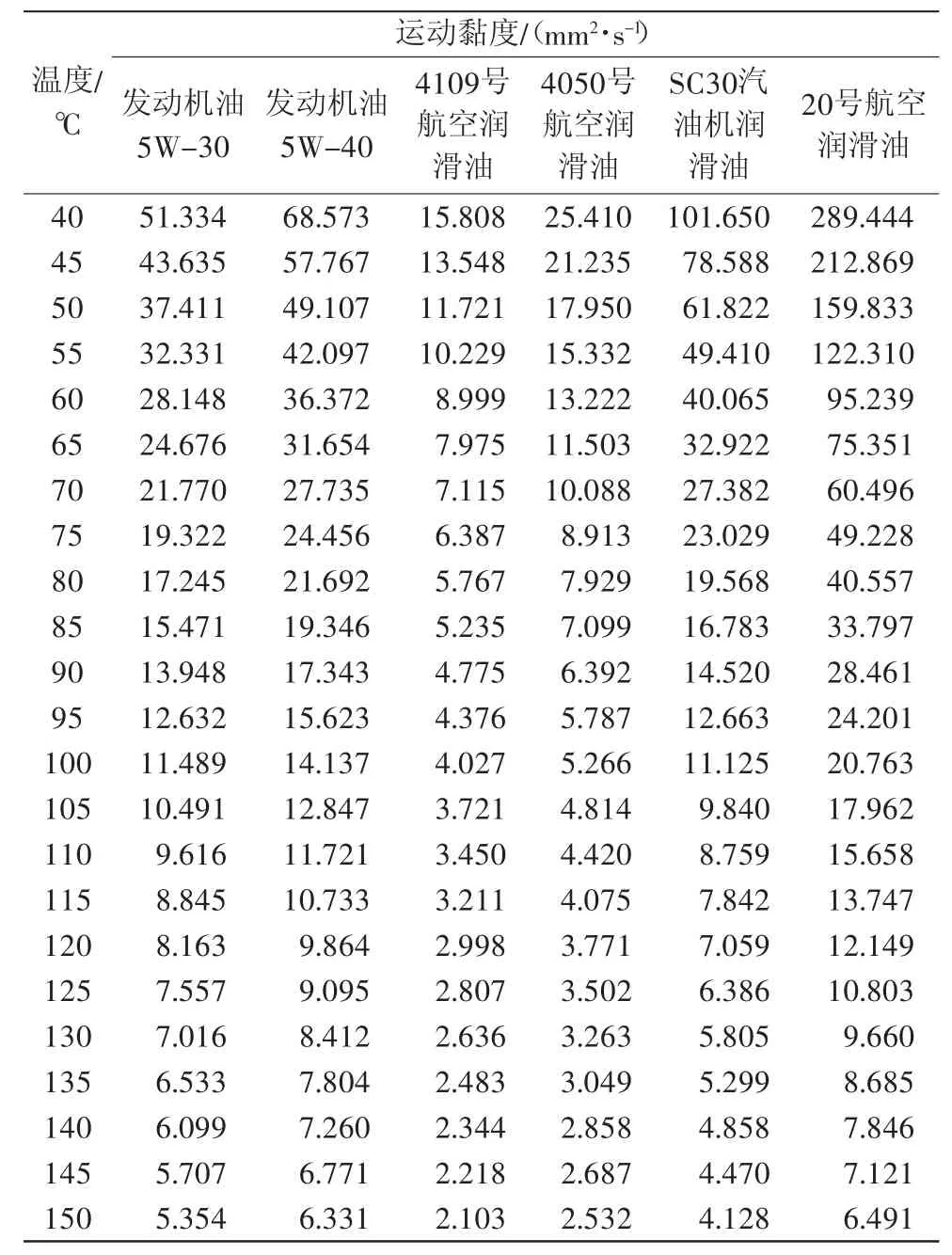
表5 润滑油的运动黏度
将得到的润滑油运动黏度代入到齿轮的啮合效率公式,可得到齿轮在各润滑油不同温度下的啮合效率,如图2所示。

图2 温度与齿轮啮合效率的关系曲线
通过实验测定的黏度值可知,在低温段,温度对黏度的影响比较大;在高温段,温度对黏度的影响逐渐变小,尤其在40~100 ℃温度段运动黏度下降幅度比较大,当温度在100 ℃以上时,运动黏度下降的幅度逐渐减小,黏温曲线逐渐平缓。
温度升高促使润滑油黏度下降,导致齿轮的啮合摩擦因数增大,使得滑动摩擦损失增加,导致齿轮的啮合效率降低。并且温度对齿轮啮合效率的影响规律呈现近似的线性递减关系。
2.2 压力对啮合效率的影响
压力对润滑油黏度影响的Barus公式[12-13]表示为
式中:P为压强,μ0为润滑油在环境压力下的动力黏度,α为压力与黏度的系数。
润滑油密度与压力和温度的关系式可以采用Dowson-Higginson公式[14]表示为
式中:ρ0为润滑油的环境密度,β1为润滑油的热膨胀系数。
润滑油在压力为P时的运动黏度为
下面以PAO-186合成油为例,通过编程可得PAO-186合成油在温度分别为40、80、100 ℃下的运动黏度,如表6所示。

表6 不同压力下PAO-186合成油的运动黏度mm2/s
将得到的润滑油运动黏度代入到齿轮的啮合效率公式,如图3所示,可得到在润滑油不同压力下的齿轮啮合效率。由图3可知,当润滑油的压力增大时,分子间的距离缩短,吸引力增大,所以润滑油的运动黏度会升高,导致齿轮啮合摩擦因数减小,使得滑动摩擦损失降低,导致齿轮的啮合效率增大。齿轮啮合效率与润滑油压力成线性递增关系。

图3 齿轮啮合效率随压力的变化曲线
3 啮合效率优化分析
3.1 啮合效率优化数学模型
A.Schmidt等[15]基于Barus公式,提出任意温度t和压力P下的动力黏度经验公式如下:
式中,参数a1、a2、b1和b2是通过实验数据计算得到的。
齿轮啮合效率都是设计参数的单调递增或单调递减函数,因此需要引入适当的约束条件,参数优化才是有意义的。因此齿轮啮合效率优化问题转化为约束最优化问题。约束最优化设计包含设计变量、约束条件和优化目标函数。
设计变量为
约束条件为:
式中:gi(i=1,2,…,m)为不等式约束条件;hj(j=1,2,…,l)为等式约束条件;分别为xk(k=1,2,…,n)的上下限。
优化目标函数为
式中,f(x)为齿轮的啮合效率。
优化时选择对啮合效率影响较大的参数,本文选取法向压力角、法向模数、齿顶高系数和螺旋角作为设计变量,设计变量表示为向量的形式如下:
本文设置约束条件如下:法向压力角αn取20.0°、22.5°、25.0°;根据GB/T 1357—1987标准,法向模数mn选1.5、2.0、2.5、3.0 mm;齿顶高系数han范围为0.9~1.1;螺旋角β范围为5°~25°。
3.2 齿轮啮合效率优化
环境温度t为60 ℃,环境压力P为0.05 MPa,通过计算求解,得到法向压力角分别为20.0°、22.5°、25.0°时不同法向模数下优化前后啮合效率与动力黏度的关系对比曲线,分别如图4~图6所示。

图4 法向压力角为20°时,啮合效率与动力黏度的变化曲线
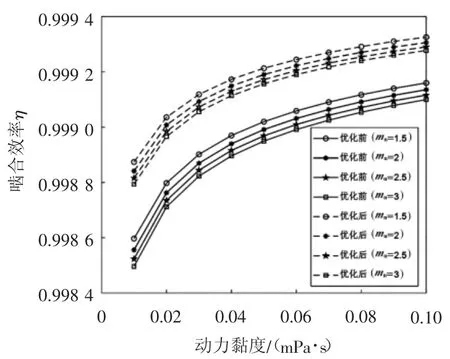
图5 法向压力角为22.5°时,啮合效率与动力黏度的变化曲线
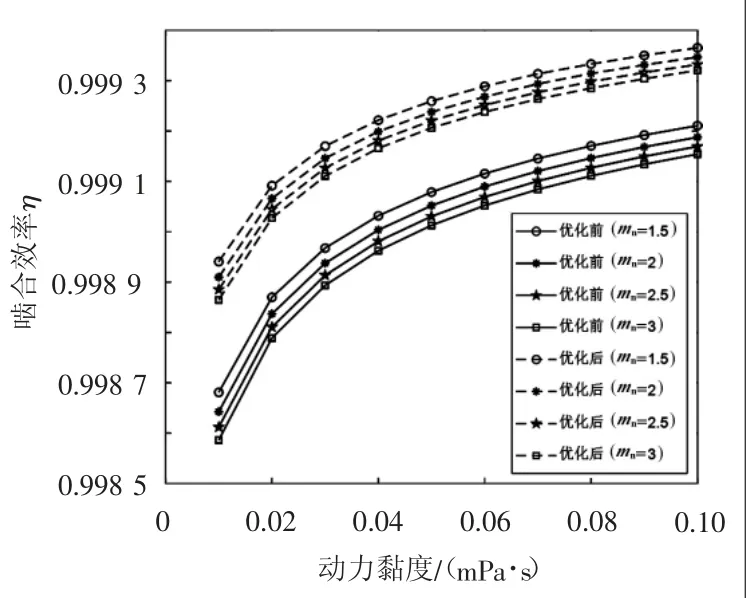
图6 法向压力角为25°时,啮合效率与动力黏度的变化曲线
结合上述结果,在可行域范围内,当法向压力角αn为25°且法向模数mn为1.5 mm 时,对应的动力黏度下的啮合效率最高。当法向压力角增大时,导致啮入起点滑移率和啮出终点滑移率都减小,从而使啮合机械功率损耗减小,啮合效率增加。当法向模数减小时,导致切向节线速度减小,载荷强度增大,进而导致齿轮啮合摩擦因数减小,从而功率损耗减小,啮合效率增加。
在动力黏度为0.04 mPa·s、法向压力角αn为25°和法向模数mn为1.5 mm的情况下,无优化时的齿顶高系数han为1,螺旋角β为10°,计算得到的啮合效率为99.903%;优化后齿顶高系数han为0.901,螺旋角β为24.979°,计算得到的优化啮合效率为99.922%,可提高0.019%,可减少长时间运转系统的热量损耗。因此,在极端天气(如高温和低压情况)下,为保证齿轮的啮合效率,可以降低法向模数和齿顶高系数,提高法向压力角和螺旋角,合理搭配齿轮参数,选择满足啮合效率的润滑油。
4 结语
本文建立考虑润滑油温度和压力对齿面摩擦特性影响的啮合效率计算数学模型,分析了温度和压力对齿轮啮合效率的影响规律,并提出啮合效率优化方案,得到如下结论:1)温度升高时黏度下降,导致齿轮的啮合摩擦因数增大,使得滑动摩擦损失增加,导致齿轮的啮合效率降低;2)当润滑油的压力增大时,分子间的距离缩短,吸引力增大,所以润滑油的黏度会升高,导致齿轮啮合摩擦因数减小,使得滑动摩擦损失降低,导致齿轮的啮合效率增大;3)在高温和低压情况下,合理搭配齿轮参数,选择合适的润滑油,可以适当地提高齿轮的啮合效率。
