摆线齿轮滚齿切削力及温度仿真分析
2023-10-14马付建高小迪普斌马嘉恒宗梓范
马付建,高小迪,普斌,马嘉恒,宗梓范
(大连交通大学 机械工程学院,辽宁 大连 116028)
RV减速器是一种常用的精密减速器,其核心机构是由双摆线齿轮与针轮及曲柄配合而成的二级减速机构,其中双摆线齿轮的齿形精度直接影响到RV减速器的传动精度[1-2]。摆线齿轮滚齿的加工方法主要有插齿加工、滚齿加工、铣齿加工及线切割加工等[3],其中滚齿加工是摆线齿轮加工的一种主要方式。RV减速器中摆线齿轮对齿廓精度要求高,而滚齿加工中的切削力和切削温度均会对摆线齿轮齿廓加工精度有较大影响,为此,国内外研究人员针对滚齿加工中的切削力和切削温度开展了相关研究。Sabkhi等[3-4]通过CAD软件布尔运算对渐开线滚齿加工过程中的未变形切屑几何体进行了建模,并基于微元法建立了离散化刀刃切削力,分析了切削力随滚齿速度变化规律。李钧亮[5]通过推导计算渐开线滚齿加工未变形切屑几何模型体积及K-V力学公式,建立了受切屑厚度和宽度影响的滚齿加工切削力模型。周力等[6]基于有限元方法对渐开线齿轮滚齿加工进行了仿真分析,研究了不同工件材料及加工参数下的切削力及切削温度变化规律。王新宇[7]对渐开线齿轮滚齿加工单齿切削建立了有限元仿真模型,分析了切削热随加工时间变化的规律。
以上研究大多从切削参数对切削力和切削温度的影响规律方面进行研究,而以摆线齿轮为研究对象进行研究的文献较少,其影响规律和影响程度尚不清楚。鉴于此,本文以某摆线齿轮为研究对象,建立摆线齿轮加工中间体和滚刀几何模型,对摆线齿轮滚齿加工运动过程进行分析,建立加工运动方程,并基于此建立摆线齿轮滚齿加工热力耦合有限元分析模型,研究轴向进给量和滚切速度对摆线齿轮滚齿切削力及切削温度的影响规律。
1 滚刀及加工中间体几何模型
1.1 摆线齿轮滚刀建模
本文使用的摆线齿轮齿形为圆弧-短幅外摆线等距线齿廓,摆线齿轮与针轮实际配合过程属于包心运动[8],即摆线齿轮基圆在针轮基圆内做纯滚动,摆线齿轮中心绕针轮中心回转,针轮中心不动。为方便计算,假设摆线齿轮不动,针轮基圆在摆线齿轮基圆上纯滚动,针轮中心绕摆齿线轮中心回转,如图1所示。

图1 圆弧-短幅外摆线形成过程示意图

(1)

本文根据摆线齿轮与针轮啮合运动关系,基于齐次坐标变换及多系统运动学原理,建立摆线齿轮齿形方程与针轮齿形方程的关系为:
(2)
式中:φ=φ2-φ1。
根据摆线齿轮和针轮啮合传动中传动比与转角间的关系,可以推出:
(3)
将式(1)、式(2)和式(3)联立,可将摆线齿轮的齿形方程表达为:
(4)
根据齿轮啮合原理和共轭曲线理论可知,摆线齿轮齿形与滚刀刀刃法向齿形的运动关系,与齿轮与齿条配合关系相同。因此,摆线齿轮的节圆在齿条的节线上做纯滚动时,摆线齿轮包络出的齿形即为滚刀齿形,其啮合过程见图2。

(5)
摆线齿形基本参数如下:针轮圆半径R2为82 mm;中心距e为1.5 mm;摆线齿轮基圆半径r1为38.5 mm;针轮圆基圆半径r2为40 mm;针轮针齿半径rz为7 mm;中心距转角0°≤φ1≤360°。将摆线齿形基本参数代入式(4),并将式(4)求得的结果代入式(5),得到滚刀基本参数如下:滚刀外径D为75 mm;滚刀容屑槽数为12;滚刀头数为3;滚刀长度L为110 mm;滚刀螺旋升角λ为3.136°;铲背量值h为5.4 mm。结合滚刀基本参数,建立滚刀的三维结构模型,见图3。

(a) 正视图
1.2 加工中间体建模
加工中间体是指齿轮在滚齿加工中齿坯到零件的中间形态。加工中间体建模时需要先对滚齿加工运动进行分析,通过滚刀刀刃上的点在滚齿加工运动过程中形成的空间轨迹曲面簇,与工件齿坯进行布尔运算,从而得到加工中间体模型。
滚齿加工过程中刀具与工件的相对位置和运动关系见图4。图中共设置5个坐标系,分别为固定参考坐标系OrXrYrZr、刀具参考坐标系O1X1Y1Z1、工件参考坐标系O2X2Y2Z2、刀具固联坐标系OhXhYhZh以及工件固联坐标系OgXgYgZg。

图4 工件与刀具空间位置及运动关系
图4中刀具与工件的相对运动关系如下:
(1)刀具回转运动
刀具固联坐标系OhXhYhZh在加工过程中绕X1轴回转运动,刀具运动相位角用φ表示,刀具回转运动用矩阵Rx(φ)表示:
(6)
(2)刀具轴向进给运动
刀具相对于工件的轴向进给,在固定参考坐标系OrXrYrZr中进行,刀具沿工件轴向进给加工出工件全齿宽,轴向进给量可用矩阵Tz(ζ(φ))表示:
(7)
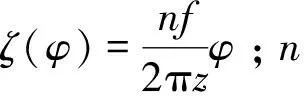
(3)工件回转运动
工件固联坐标系OgXgYgZg在加工过程中绕Z3轴回转运动,工件与刀具按照传动比关系分别绕自身轴线回转以保证得到正确的齿形,工件回转运动可用矩阵Rz(ψ(φ))表示:
(8)

将刀具与工件的运动用齐次坐标变换矩阵表示,则滚齿加工运动方程为:
Rtrans(φ)=Rz(ψ(φ))Tz(ζ(φ))Rx(φ)
(9)
滚刀上某个刀刃用矩阵E(t)=[Xc′(t),Yc′(t),Zc′(t),1]T表示,t为该刀刃所在位置的角度区间。通过E(t)建立滚刀刀刃组的空间坐标系Ei(t),其中i代表滚刀刀齿的序号。进行齐次坐标变换后,滚刀刀刃则在工件坐标系OgXgYgZg中完成包络运动,形成空间轨迹曲面簇,其矩阵方程为:
Gi(t)=Rtrans(φ)E(t)i
(10)
当刀具转角φ=128π时,滚刀刀刃在工件坐标系OgXgYgZg中形成空间轨迹曲面簇,见图5。在径向切深为全齿高, 轴向进给为开始形成完整齿形位置,将空间轨迹曲面簇在齿坯模型上进行布尔运算,得到某一时刻的齿槽模型,见图6。

图5 滚刀刀刃的空间轨迹曲面簇

图6 加工中间体模型
2 摆线齿轮滚齿三维仿真过程
2.1 刀具与工件材料属性
摆线齿轮的材质为25CrMo4,泊松比为0.3,密度为7.85×10-6kg/mm3,其他参数随温度变化的材料属性见表1。滚齿刀具材料为M35,泊松比为0.23,热导率为30 W/(m·K),比热容为15 J/(kg·K),密度为8.14×10-6kg/mm3。

表1 25CrMo4材料属性
2.2 材料本构模型
滚齿加工过程中,材料将发生非线性变形,产生大应变。本文采用Jonhson-Cook本构模型,该模型适用于表征滚齿加工过程的高应变率、大应变值及塑性耗散导致的材料软化,其本构模型关系为[9]:
(11)
滚削仿真中,存在切屑分离的过程,因此需对材料断裂准则进行分析与设定。考虑滚齿加工断续切削的加工特点,选择Johnson-Cook断裂应变模型。其表达方程为[9]:
(12)

材料本构参数及切削分离参数如下:d1为0.1;d2为0.76;d3为1.57;d4为0.005;d5为-0.84;加工硬化指数n为0.2;应变率系数C为0.02;室温Troom为20 ℃;材料熔点Tmelt为1 527 ℃;软化系数为0.64。
2.3 滚齿切削有限元仿真模型建立
本文在deform-3d仿真软件中对刀具及工件进行几何建模。为提升仿真效率,对工件进行裁剪,由于滚齿加工是断续非自由切削,每刀刀齿对工件齿槽的切削进给量小、切削速度快、切屑厚度薄,使得切削力及切削时间远小于连续切削加工方法,且滚齿加工工件刚度大,因此仅保留切削影响区及邻近部分特征进行切削加工仿真,不会使整体工件的滚齿切削加工仿真产生技术性误差。将切削区的单元网格划分为0.01 mm,其他区域划分为0.1 mm。在滚齿加工过程中,刀具的刚度要远大于工件刚度且在分析中加工的时间较短,不考虑刀具磨损、变形等对切削力与切削热的影响,刀具为刚体,对刀具按照式(9)施加运动约束。工件底部施加轴向固定约束,对工件裁剪面施加对称约束。仿真过程设为油液冷却,系统热对流系数设为125W/(m2·K),建立的摆线齿轮滚削有限元仿真模型见图7。

图7 摆线齿轮滚削有限元仿真模型
3 仿真试验及结果分析
3.1 仿真试验设计
本文通过对摆线齿轮滚齿加工进行仿真,研究不同滚齿切削速度和轴向进给量对摆线齿轮滚齿加工切削力及切削温度的影响。仿真中采用的滚齿加工参数如下: 滚齿切削速度分别为300、450、600、750、900 r/min;轴向进给量分别为0.25、0.5、0.75、1 mm/r。
图8为滚齿切削速度在600 r/min、轴向进给量为0.5 mm/r时,滚齿切削过程切削力及切削温度随加工时间的变化曲线。

(b) 径向切削力随加工时间变化
根据金属切削原理可知,切屑厚度和宽度是切削力的重要影响因素。通过对滚齿加工过程的运动分析可知,任意一个齿槽的第i个包络面与第i-1个包络面之间的几何体,即为加工第i个包络面所形成的未变形切屑几何模型,未变形切屑几何模型表达式为:
Gi-1→i(t,φ)=Rtrans(φ)E(t)i-Rtrans(φ)E(t)i-1
(13)
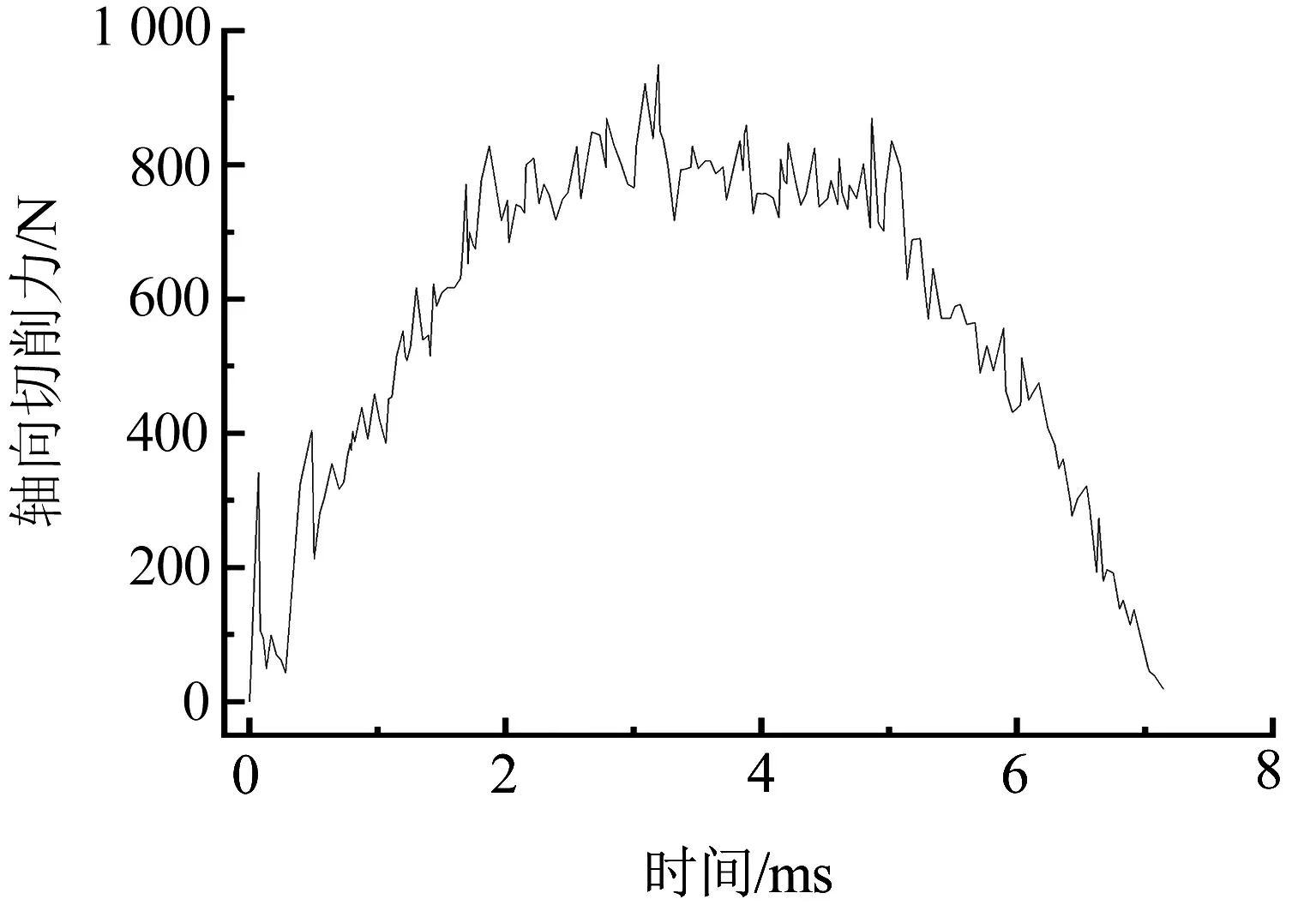
(a) 轴向切削力随加工时间变化
由图8(a)可知,在0~2 ms为切入阶段,轴向切削力上升至800 N左右,在2~5 ms轴向切削力进入平稳阶段,在5~7.1 ms轴向切削力随加工时间开始下降,轴向切削力曲线整体呈抛物线形。由式(13)可知, 切屑宽度和厚度的主要影响因素分别为
sin2(φ)sin2(ψ(φ))cos(ψ(φ))cos(φ)ζ(φ)、
cos2(φ)cos2(ψ(φ))sin(ψ(φ))sin(φ)ζ(φ)
滚刀切入角φ=0°,切出角φ=24.075°,剪切区面积在加工过程中由小到大再减小,轴向切削力主要受剪切区面积变化影响,因此轴向切削力随加工时间的变化与剪切区面积变化趋势相同,均为先增大后减小。由于剪切区面积在11.5°~20.5°没有明显变化,对应的加工时间约为2~5 ms,其轴向切削力处于稳定切削阶段,因此在分析切削参数对轴向切削力的影响规律时,选取2~5 ms时间段的轴向切削力的平均值进行分析。
由图8(b)可知,在0~1.6 ms径向切削力快速上升至430 N左右,在1.6~7.1 ms径向切削力持续下降。由式(13)可知,在0~1.6 ms滚刀切入工件,剪切区面积开始增大使得径向切削力逐渐增大;在1.5~7.1 ms径向切削力受刀具转角不断增大和剪切区面积逐渐减小的综合影响,开始随加工时间逐渐减小,直至刀具完全切出工件。1~3 ms时间段内的径向切削力相对比较稳定,因此在分析切削参数对径向切削力的影响规律时,选取该段切削力的平均值进行分析。
由图8(c)可知,在开始阶段,切削温度快速上升到250 ℃左右后逐渐趋于平缓,随后在切屑带走部分热量以及切削液冷却的影响下,切削温度稳定在250~290 ℃区间内,在刀具完全切出工件后温度曲线不再波动且呈稳定下降趋势,与实际加工情况相符合。在1.5~6.5 ms范围内,切削温度相对比较稳定,因此在分析切削参数对切削温度的影响规律时,选取1.5~6.5 ms时间段的温度平均值进行分析。
3.2 加工参数对切削力的影响
本文利用建立的摆线齿轮滚齿切削有限元仿真模型,根据滚齿加工参数进行滚齿仿真,得到摆线齿轮滚齿加工切削力随加工参数的变化曲线,见图9。
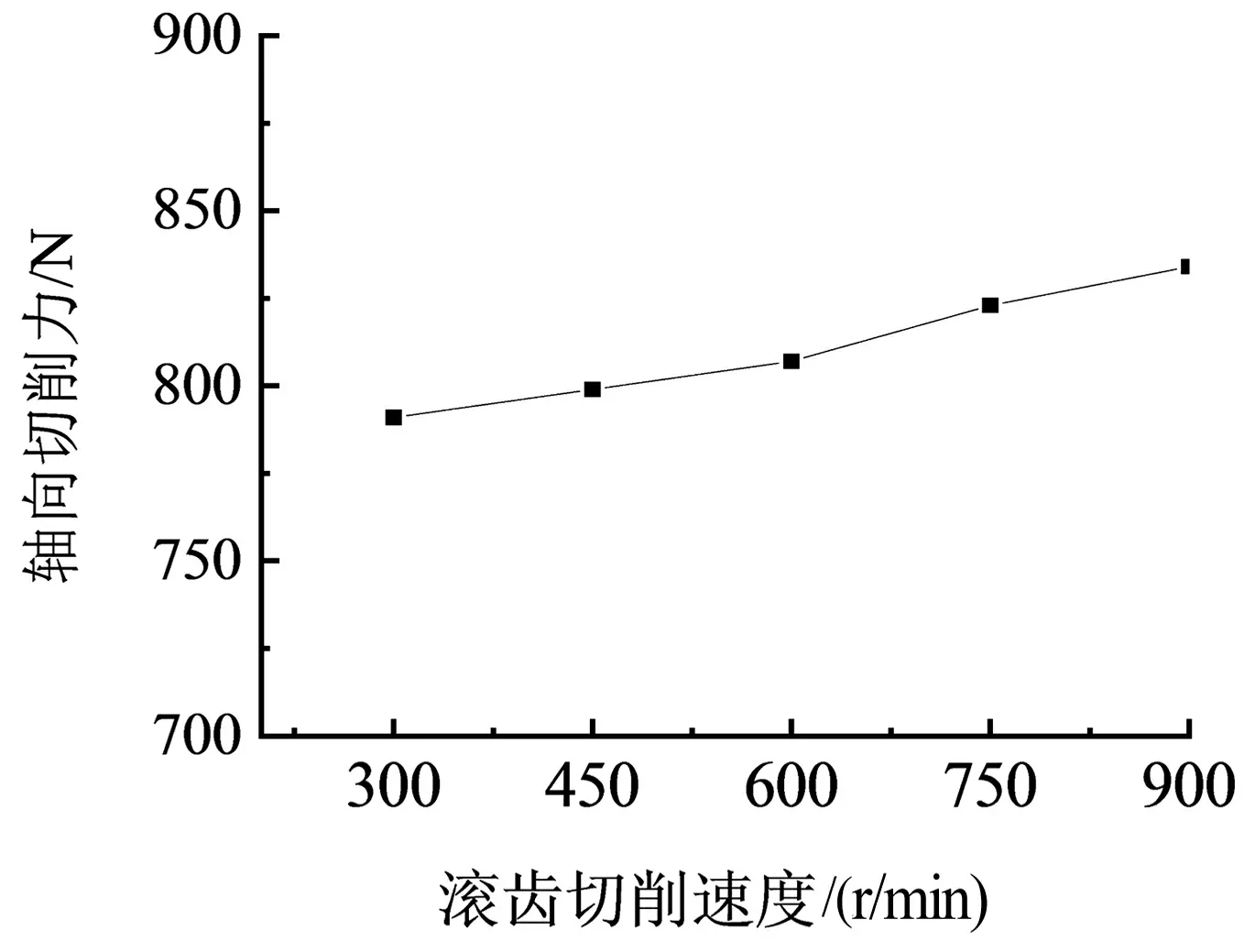
(a) 滚齿切削速度对轴向切削力
由图9(a)可知,滚齿切削速度对轴向切削力影响相对较小,当滚齿切削速度从300 r/min增大到900 r/min时,轴向切削力由791 N逐渐上升到834 N。
由图9(b)可知,当轴向进给量从0.25 mm/r增至0.75 mm/r时,轴向切削力上升较慢,从803 N上升到823 N;当轴向进给量由0.75 mm/r增大到1 mm/r时,轴向切削力上升较快,从823 N上升到914 N。
对比图9(a)和9(b),在滚齿切削速度从300 r/min上升至900 r/min的过程中,轴向切削力上升了42 N;在轴向进给量从0.25 mm/r上升至1 mm/r的过程中,轴向切削力上升了91 N,因此可以判断轴向进给量对轴向切削力的影响要大于滚齿切削速度。
由图9(c)可知,当轴向进给量从0.25 mm/r上升至0.75 mm/r时,径向切削力从324 N上升至407 N,大约上升了10%。当轴向进给量从0.75 mm/r上升到1 mm/r时,径向切削力从407 N上升至554 N,上升约35%。
3.3 加工参数对切削温度的影响
根据滚齿加工参数的滚齿加工仿真结果,得到摆线齿轮滚齿加工中加工参数对切削温度的影响曲线,见图10。

(a) 滚齿切削速度对切削温度
由图10(a)可知,滚齿切削速度越大,切削温度也越高,滚齿切削速度从300 r/min上升至450 r/min的过程中,切削温度比较缓慢地从229 ℃上升至232 ℃;滚齿切削速度从450 r/min上升至900 r/min的过程中,切削温度比较快速地从232 ℃上升至274 ℃。由图10(b)可知,轴向进给量从0.25 mm/r上升至0.75 mm/r的过程中,切削温度从225 ℃上升至244 ℃,上升速度较慢;轴向进给量从0.75 mm/r上升至1 mm/r的过程中,切削温度从244 ℃上升至273 ℃,上升速度较快。
4 结论
本文基于Deform-3D有限元分析软件建立了摆线齿轮滚齿切削仿真模型,研究了加工过程中的切削力及切削温度随时间和加工参数变化的规律,得到如下结论:
(1)轴向切削力在切入阶段,随加工时间快速增大,然后进入切削力在一定范围内波动的稳定切削阶段,在切出阶段迅速降低;径向切削力在切入阶段快速上升至最大值,随后随加工时间逐渐减小。切削温度在开始阶段快速升高,随后缓慢升高至平稳阶段,平稳阶段的温度在一定范围内波动。
(2)当轴向进给量从0.25 mm/r增大到0.75 mm/r时,轴向切削力和径向切削力分别增加了20 N和36 N,增加速度较慢;当轴向进给量从0.75 mm/r增加到1 mm/r时,轴向切削力和径向切削力分别增加了91 N和146 N,增加速度较快。滚齿速度从300 r/min增大到900 r/min时,轴向切削力增大了43 N,滚齿切削速度对轴向切削力的影响小于轴向进给量的影响。因此,提升生产效率可以通过合理提高滚齿切削速度来实现,但提高轴向进给量需谨慎考虑。
(3)滚齿切削速度从300 r/min增大到450 r/min的区间内,切削温度上升了3 ℃,上升速度比较缓慢;滚齿切削速度从450 r/min增大到900 r/min的区间内,切削温度上升了42 ℃,上升速度较快。当轴向进给量从0.25 mm/r增大到0.75 mm/r时,切削温度上升了19 ℃,上升速度较慢;当轴向进给量从0.25 mm/r增大到0.75 mm/r时,切削温度上升了29 ℃,上升速度较快。因此,对加工温度较为敏感时,可将轴向进给量可以控制在0.75 mm/r以下。
