基于复数滤波器的三相锁相环技术改进策略
2023-10-14鞠艳杰何帮鹏
鞠艳杰,何帮鹏
(大连交通大学 自动化与电气工程学院,辽宁 大连 116028)
随着清洁能源(风能、太阳能等)的广泛利用,基于并网逆变器的并网技术也得到了更多的关注。并网逆变器的运行和控制需要电网电压同步信号的信息,而锁相环技术是实现这一功能的主要方式,因而得到了各国学者的广泛研究和应用。
在三相锁相环的研究中,较为成熟的技术有同步旋转坐标系锁相环(Synchronous Rotating Frame PLL,SRF-PLL)[1-2]、解耦双同步坐标系锁相环(Decouple Double Synchronous Rotating Frame PLL,DDSRF-PLL)[3]、自适应陷波器型锁相环(Adaptive Notch Filter PLL,ANF-PLL)[4]、双二阶广义积分器型锁相环(Double Second-Order Generalized Integrator PLL,DSOGI-PLL)[5-6]和复数滤波器型锁相环(Complex Coefficient Filter PLL,CCF-PLL)[7-8]。其中,CCF-PLL由于其控制结构简单、响应速度快和具有正负频率的选择性等优势,受到广泛关注。谢永强等[9]在静止坐标系锁相环的基础上,利用复数滤波器进行解耦提取正序电压的方法来提高锁相性能。党克等[10]提出多重复数滤波器与锁频环相结合,利用多重复数滤波器分离正序分量与谐波,锁频环进行电网锁相跟踪,从而改进了锁相环的性能。参考相关文献后不难发现,CCF-PLL在多种故障条件下的锁相性能都满足国家标准。然而,其在电网电压不对称情况下的输出频率波动较大,锁相性能可进一步优化。
综上所述,为提升传统CCF-PLL在非理想电网条件下的估计信息功能,本文提出了一种改进型CCF-PLL方案。该方案利用前置SOGI进行输入信号的滤波,然后通过CCF提取基波正序分量,再添加后置SOGI对不平衡情况(尤其是电压幅值跌落的情况)进行调节,并且改变前级CCF与后级SRF之间的反馈信号,从而使得该锁相环在不平衡情况下能够更好地锁相。仿真结果表明,所提出的锁相环比CCF-PLL能够更加精确地在各种故障条件下锁相,提高了系统性能及适用性。
1 CCF-PLL
1.1 CCF-PLL工作原理
复数滤波器型锁相环(CCF-PLL)采用图1所示的结构图。首先,该锁相环将输入的三相电压Uabc进行Clark变换,得到静止坐标系(αβ)下的电压Uαβ;其次,Uαβ通过复数滤波器进行滤波和提取基波正序分量,然后对提取出的正序分量进行Park变换得到同步旋转坐标系(dq)下的电压Uq;最后,利用传统的SRF-PLL提取电网电压的频率和相位。CCF的结构图可以分为CCF滤波模块和SRF-PLL两部分,前级的CCF负责提取输入电压的基波正负序分量,后级的SRF-PLL利用前级提取的正序分量进行锁相,从而得到电网电压的频率和相位等信息,前后两级通过ω0进行关联,并且能够在一定程度上实现频率的自适应。

图1 CCF-PLL的结构图
1.2 复数滤波器的推导
对CCF-PLL的结构图进行详细分析,由图1可推导出复数滤波器的数学模型表达式为:
(1)
整理式(1)可得:
(2)

(3)
滤波器F+(s)的幅频特性为:
(4)
滤波器F-(s)的幅频特性为:
(5)
F+(s)和F-(s)的bode图见图2。
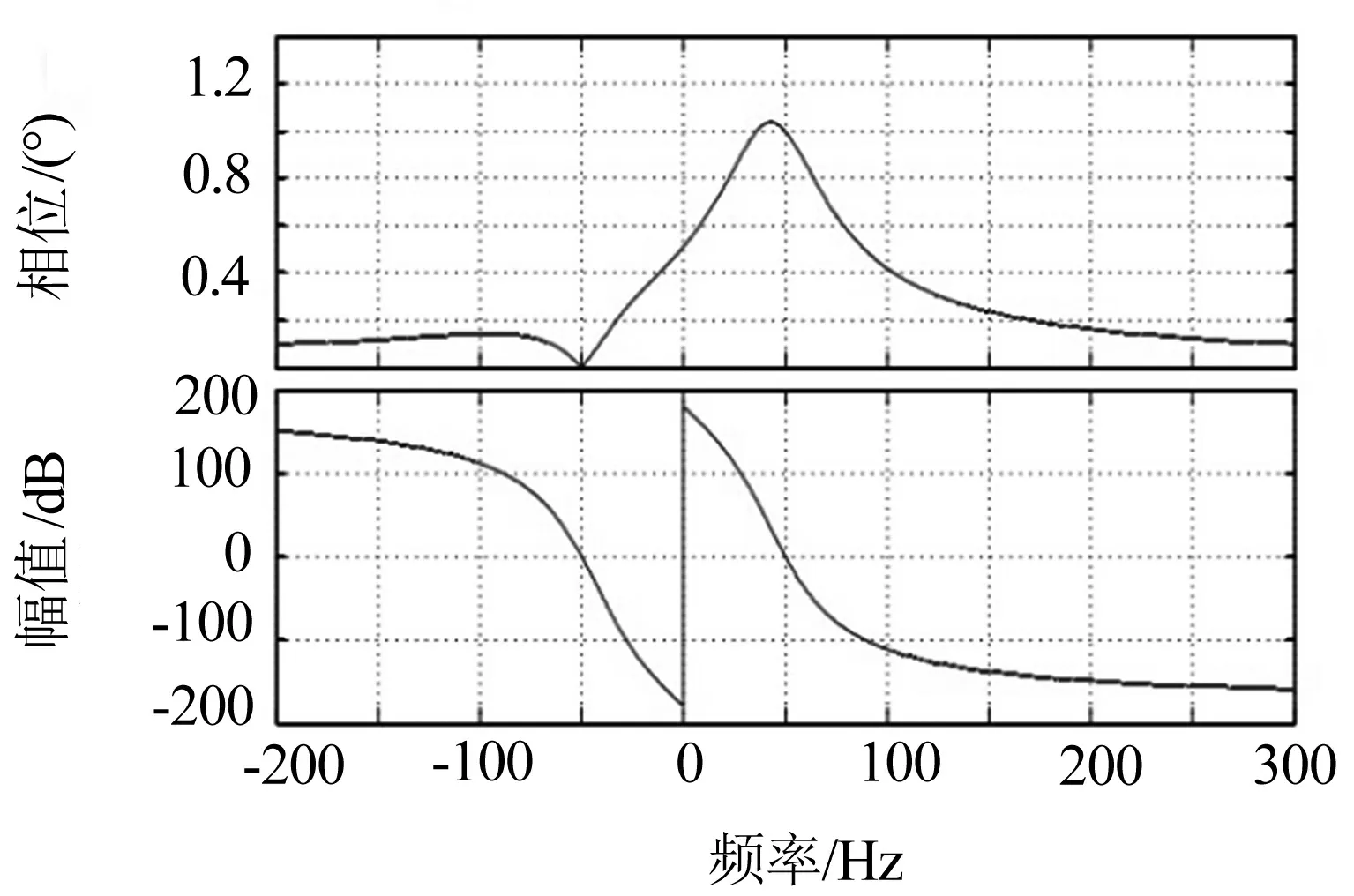
(a) 正序滤波器F+(s)的bode图
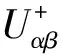
1.3 复数滤波器的实现形式
由于正负序滤波器F+(s)和F-(s)的实现方式有很多种,本文参考文献[11]所提出的实现方式,CCF 的实现图见图3。

图3 CCF的实现图
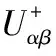
2 改进型CCF-PLL
为了改进CCF-PLL的动态性能,使得锁相环能够在各种故障状态下更加快速、准确地锁相。本文提出一种基于复数滤波器的改进型锁相环技术,其结构框图见图4。
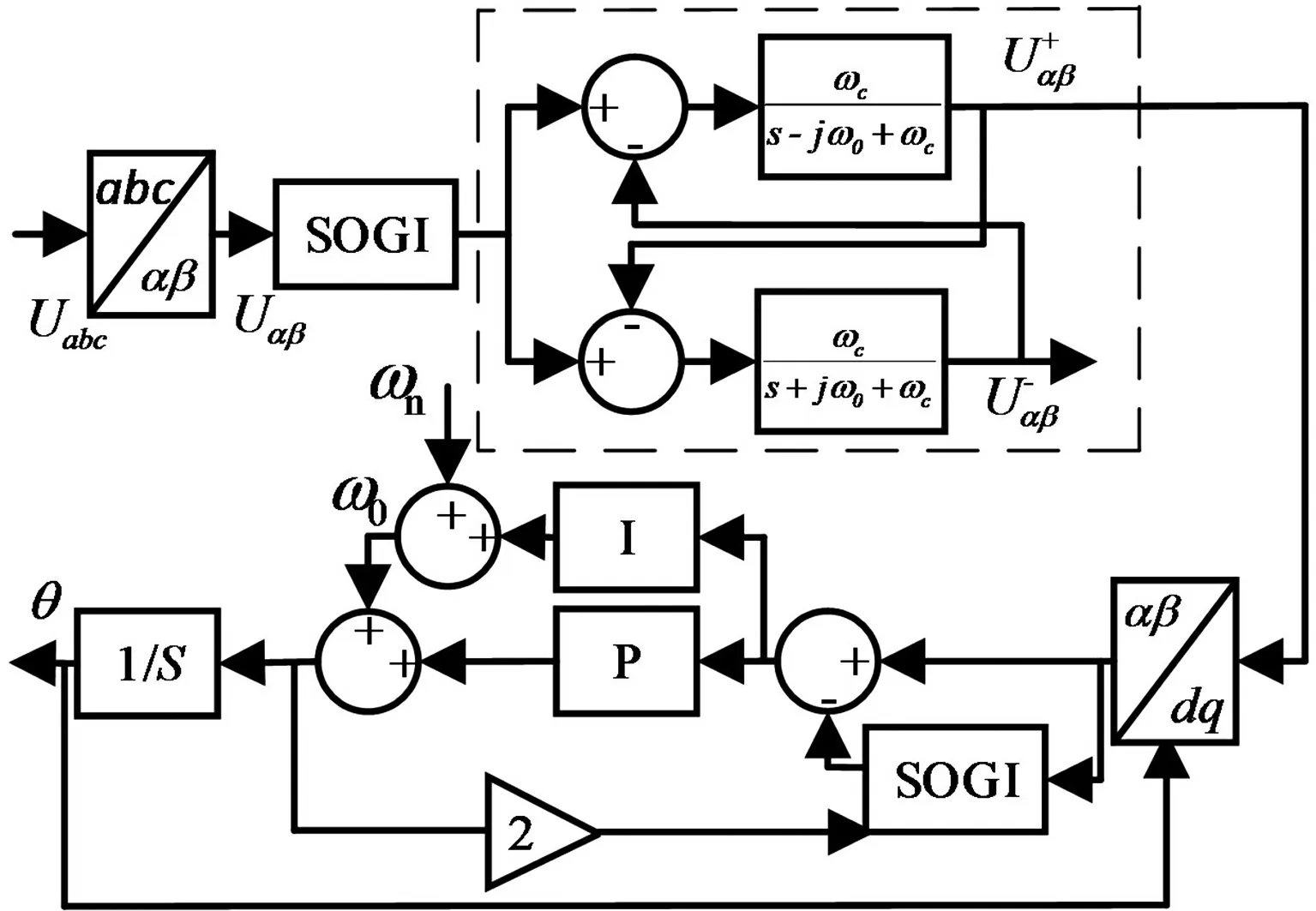
图4 改进型CCF-PLL的结构框图
本文所提出的锁相环利用前置二阶广义积分器(SOGI)对输入电压信号进行滤波,以减少电网电压中存在的谐波以及直流分量。滤波后的电压信号通过复数滤波器提取电网电压的基波正序分量,利用Park变换后所得到的q轴电压Uq,通过PI控制器的积分环节输出的角频率反馈至复数滤波器,从而使得复数滤波器能够在一定程度上具有频率适应性。此外,在PI控制器之后利用后置SOGI消除电网电压不对称情况下的q轴电压波动,从而增强CCF-PLL在电网电压不对称故障下的动态性能。
2.1 SOGI滤波
当电网处于不平衡状态时,三相电压经过Clark变换后所得到的电压中含有大量谐波分量。通常情况下都利用低通滤波器消除谐波,然而在闭环控制中会造成相位延迟,不利于锁相环工作。基于对二阶广义积分器(SOGI)的输出信号特性的研究发现,可以利用SOGI进行输入信号的滤波功能,采用图5所示的结构图。考虑到其阻尼系数k对滤波性能及响应速率产生影响,因此为了兼顾滤波和系统的快速性,k一般取1.4。

图5 SOGI的结构图
图5所示的SOGI的传递函数为:
(6)
对SOGI的传递函数进行分析,可发现输出信号v′具有带通滤波器的特性,能够抑制高次谐波和直流分量;输出信号qv′具有低通滤波器的特性,能够抑制高频干扰。所以本文利用输出信号v′的带通滤波器的特性来抑制电压中的谐波,并且可以利用此特性来消除电网电压不对称情况下所产生的二倍频干扰。
2.2 数学模型
由于经过Clark变换后,零序分量会被消除,因此输入的三相电网电压可表示为:
(7)
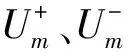
三相电压转换到两相静止坐标系可表示为:
(8)
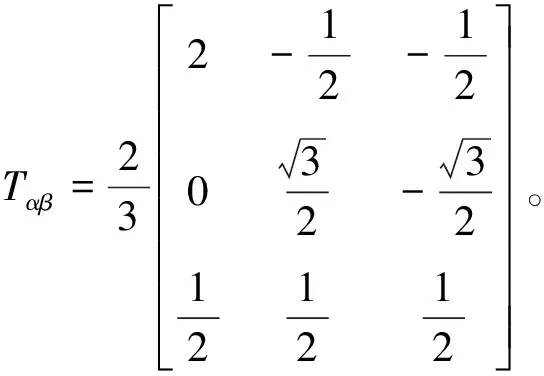
对式(8)右边进行如下定义:
(9)
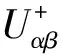
(10)
式中:θ为锁相环输出的正序分量相位角。
由锁相环的原理可推导出,θ在稳态情况下可视为正序分量的相位角,即θ=ωt+φ+。
对式(10)进行整理可得:
(11)
基于对上述数学模型的推导,可知在稳态情况下q轴坐标Uq恒定为零,且不存在负序分量二倍频的干扰,增强了锁相环的稳定性和可靠性。又由于复数滤波器提取正负分量较快的特性,使得锁相的性能更加快速准确。
2.3 反馈信号
Ghartema[12]介绍了前级复数滤波器和后级SRF-PLL之间反馈信号的选择,通常会利用压控振荡器的输入信号反馈至前级的CCF中。但这种反馈信号并不是唯一的,还可以利用PI控制器中积分器的输出作为反馈信号,文献[11]和[13]证明了改变反馈信号的有效性。此外,PI控制器中积分器的输出信号较前者更加精确,不仅保留了复数滤波器的简单性,而且没有额外增加计算负荷。
3 仿真验证
为验证所提出锁相环的正确性,本文利用MATLAB/Simulink软件对此算法进行仿真验证。仿真参数:电网电压为220 V;频率为50 Hz;CCF的截止频率为222 rad/s。本文主要研究电压不对称、直流电压和谐波3种非理想电网下锁相环的性能,设置在0.3 s时对电网电压进行故障处理,观察SRF-PLL、CCF-PLL和改进型CCF-PLL的输出并比较不同PLL的锁相性能。
3.1 电网电压不对称
当电网电压在0.3 s时发生三相电压不对称,即B相和C相电压幅值跌落为原幅值的一半,其仿真结果见图6。
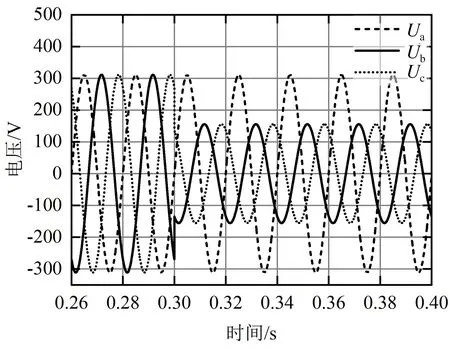
(a) 电网电压波形图
本文根据电网电压不对称故障的仿真结果,将该结果中的输出频率列于表1。

表1 电压不对称下的输出频率
结合图6和表1分析可知,在电压不对称情况下,SRF-PLL和CCF-PLL的快速性优于改进型CCF-PLL,而改进型CCF-PLL的稳态性能较优,经过0.04 s后输出频率稳定,不再波动。
图6(c)为3种锁相环的输出相位,对其进行分析可知,理想电网下相位变化呈线性关系;当发生电压不对称故障时,SRF-PLL的输出相位波动,不再呈线性关系,因而其锁相性能较差,而其他2种PLL仍呈线性关系,锁相较优。
3.2 直流电压干扰
此故障情况为A相电压在0.3 s时加入22 V的直流电压,仿真图见图7。直流干扰下的输出频率见表2。
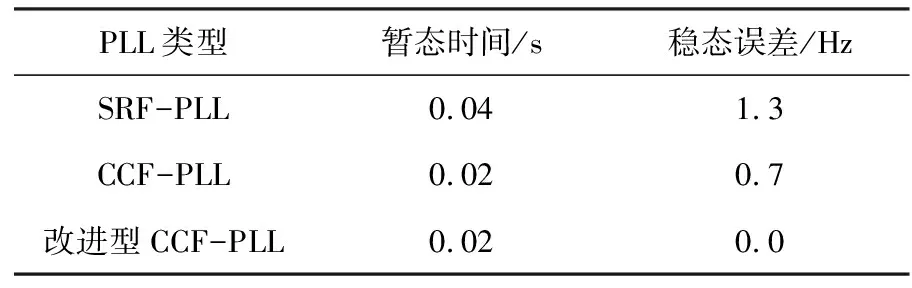
表2 直流干扰下的输出频率
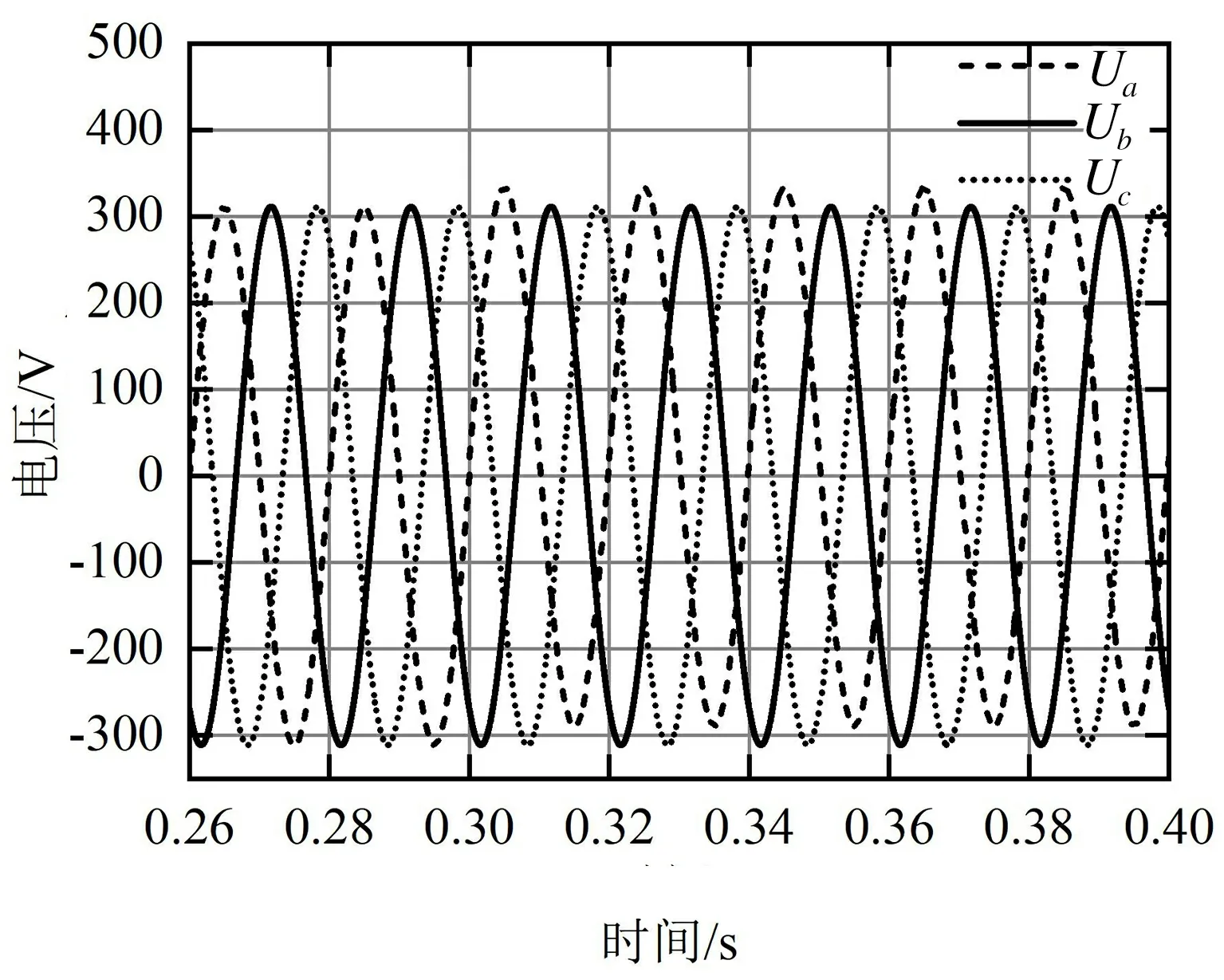
(a) 电网电压波形图
结合图7和表2分析可知,在直流干扰情况下,SRF-PLL的反应时间最长,暂态性能较差。而CCF-PLL和改进型CCF-PLL相比,改进型CCF-PLL的稳态性能更优。图7(c)中3种锁相环的输出相位在条件变化后均呈线性关系,锁相性能良好。
3.3 谐波影响
谐波下的输出频率见表3,图8为0.3 s时电网电压注入5次谐波的仿真结果。
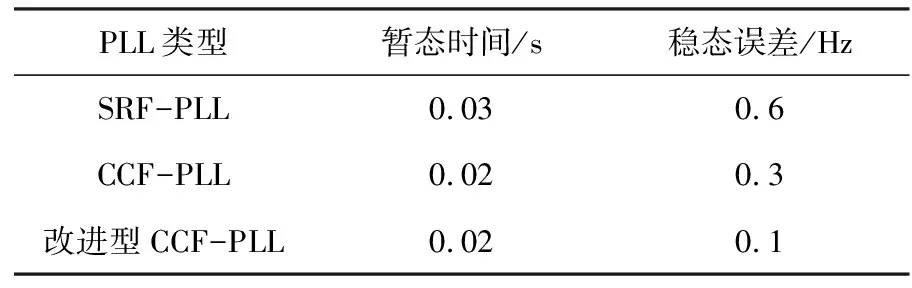
表3 谐波下的输出频率
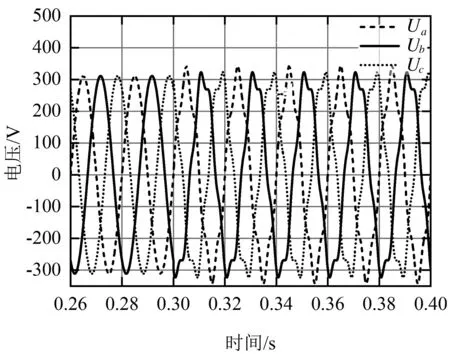
(a) 电网电压波形图
结合表3和图8分析可知,在直流干扰情况下,SRF-PLL的暂态时间较长,性能较差。稳态后3种PLL的输出频率均一直波动,但改进型CCF-PLL的误差较小,性能更优。图8(c)中3种锁相环的输出相位在条件变化后均呈线性关系,锁相性能良好。
通过仿真研究和数据对比可以得出,改进型CCF-PLL的锁相性能优于传统CCF-PLL。通过暂态时间和稳态误差的对比分析,改进型CCF-PLL的快速性和准确性均有较大提升,提高了锁相环在非理想电网下的锁相性能。
4 结论
本文提出了一种改进型锁相环的结构,在CCF-PLL的基础上,通过前置二阶广义积分器(SOGI)进行输入信号的滤波,利用复数滤波器提取基波电网电压的正序分量,改变反馈信号使得频率的反馈更加精准,最后利用后置SOGI消除在电网不对称情况下的二倍频干扰。理论分析和仿真结果都证明了所提出的锁相环在电网发生电压跌落、直流偏置以及注入谐波等故障条件下(尤其在电网电压不对称情况下)都具有更为良好的锁相性能,证明了改进型CCF-PLL的有效性。
