波纹钢管涵横断面内力计算及截面形状研究

刘晓义(安徽建工集团股份有限公司，安徽 合肥 230000)

0 引言

近年来，波纹钢管涵的排水通道模式已在国内公路系统得到明显的推广应用，众多相关的文献多偏向施工方法和质量控制方面[1-6]，对其理论研究相对偏少。目前国内应用最为广泛的波纹钢管涵主要为圆形和马蹄形两种（见图1）。理论上讲，波纹钢管涵的横断面是其整个结构的最薄弱处，而使其横断面任一截面弯矩为零则为它的最佳受力模式，图2 为零弯矩时波纹钢管涵横断面合理轴线的结构力学模型，文章以此为基础对其横断面内力及特征进行分析。

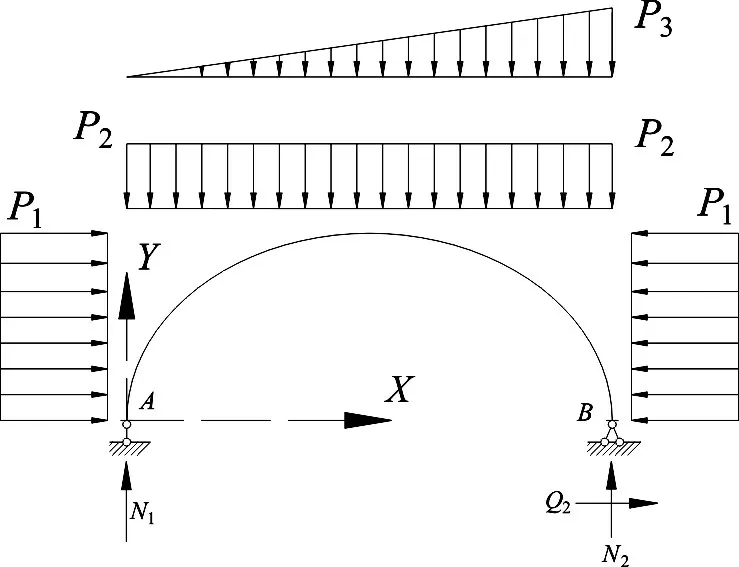
图2 零弯矩波纹钢管横断面合理轴线的结构力学模型

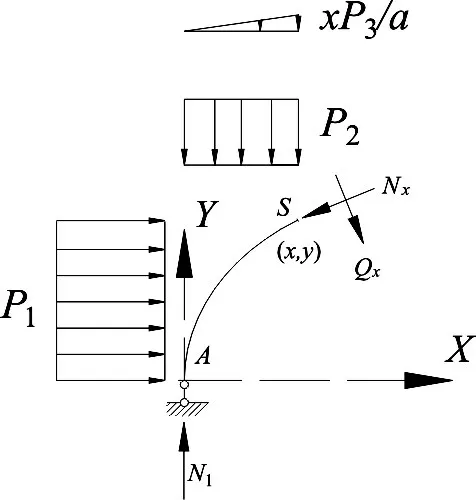
图3 零弯矩波纹钢管横断面截面内力分析

1 波纹钢管涵横断面与内力计算

1.1 波纹钢管涵横断面轴线计算

在波纹钢管横断面合理轴线设计时，需要求出合理轴线的表达式。设图2 中波纹钢管的截面为S，其坐标为（x，y），其左半部分如图2 所示，则截面S 的弯矩由四部分组成，即：

由公式（1）可知，截面S 的弯矩Ms的前三项均为沿Y 轴方向的荷载所导致的弯矩，其大小只与x 有关；后一项为沿X 轴方向的荷载所导致的弯矩，其大小只与y 有关。前三项的弯矩与对应的简支梁（如图4 所示）在受到相同的竖向荷载作用下的弯矩表达式相同，图4 中简支梁在水平坐标x 位置处的弯矩表达式如下：

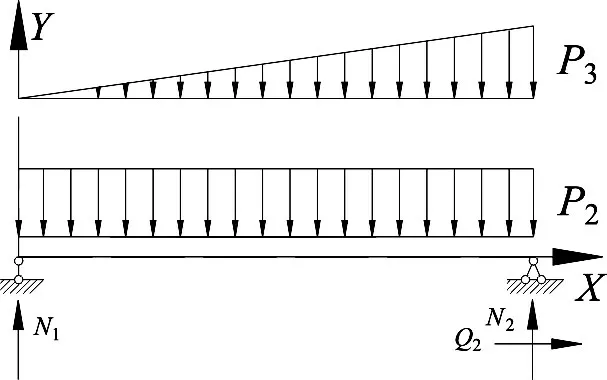
图4 零弯矩波纹钢管横断面对应的简支梁模型

若需要使截面S满足弯矩为0，则截面S的竖坐标表达式如下：

然而，图1 中波纹钢管右半部分截面为S 的弯矩由5 部分组成，如图5 所示。但是图4 中右侧大小为P1、方向向左的荷载对曲线CS 作用使截面S 产生的弯矩，与图5 中左侧大小为P1、方向向右的荷载对曲线DC 作用使截面S 产生的弯矩大小相等，方向相反，即相互抵消。因此，公式（3）适用于图2 中的任一截面，即公式3中的x取值范围为[0，a]。

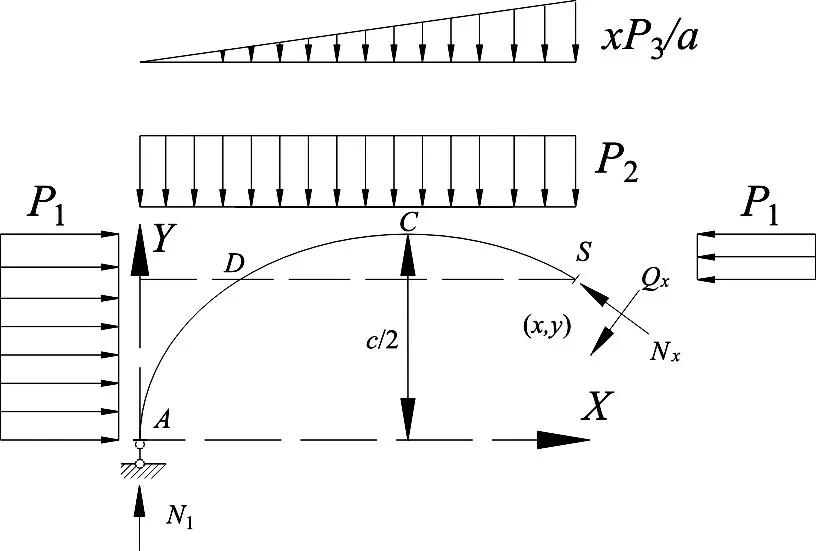
图5 零弯矩波纹钢管横断面截面内力分析

1.2 波纹钢管涵内力计算

对于横断面为合理轴线的波纹钢管涵，其横断面的内力只有轴力与剪力。设截面S 的轴力为Nx，剪力为Qx。考虑到截面的角度随坐标值的变化而变化，将截面S 的内力分解为水平荷载Fhx与竖向荷载Fvx（在图6 中分别以向左与向上为正），如图6 所示。先求出截面S 位置切线与水平线之间的角度α，再将水平荷载Fhx与竖向荷载Fvx分解为轴力为Nx与剪力为Qx（在图3 与图5 中，轴力以使截面S 受压为正，剪力以使隔离体顺时针方向旋转为正）。

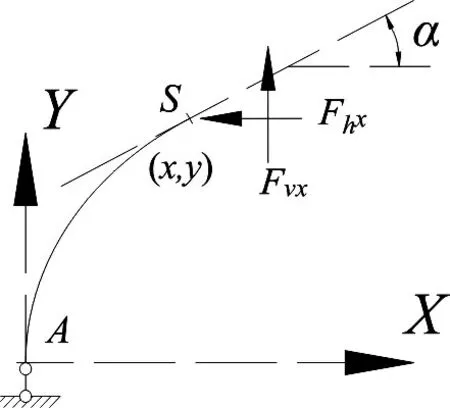
图6 零弯矩波纹钢管涵横断面截面内力分析

由∑X=0，得

由∑Y=0，得

将公式（8）对x求导得

可知角度α的表达式如下：

由Fhx、Fvx与Nx、Qx的等效关系可得

由图5 可知，当x=0 时，α=90°，ψ=tanα=+∞，sinα=1，cosα=0。

2 波纹钢管涵横断面特性分析

2.1 波纹钢管涵横断面水平直径计算

当x=a/2 时，对应的y为b/2，根据公式（3）可得到b的计算公式如下：

由图4可知，公式（11）中，x∈[ 0,a]，则当β=0 时所对应的x值计算得到的Mx值最大，因此，由β=0 时所对应的x值计算得到的y值最大，此时的y值即为c/2。当β=0时所对应的x值为：

以最大水平直径对应的竖直径位置与中心水平直径对应的竖直径位置之差作为偏心距Δo，则其计算公式为：

2.2 波纹钢管涵横断面特性

假设地层土体容重γ为19kN/m3，波纹钢管涵的竖向土压力按土柱理论计算，将交通荷载换算为地表一定厚度的上覆土，以竖直径为3m 为例，得到波纹钢管涵顶部不同理论上覆土厚度H或不同侧土压力系数k时波纹钢管涵横断面及结构内力，如表1 与表2 所示。从表1和表2中可以看出，中心水平直径b与最大水平直径c均小于竖直径a，随着波纹钢管涵顶部理论上覆土厚度的增加，中心水平直径b、最大水平直径c及偏心距Δo均减小，但减小速率越来越小；随着侧土压力系数k的增大，中心水平直径b与最大水平直径c均增大，偏心距Δo不变。

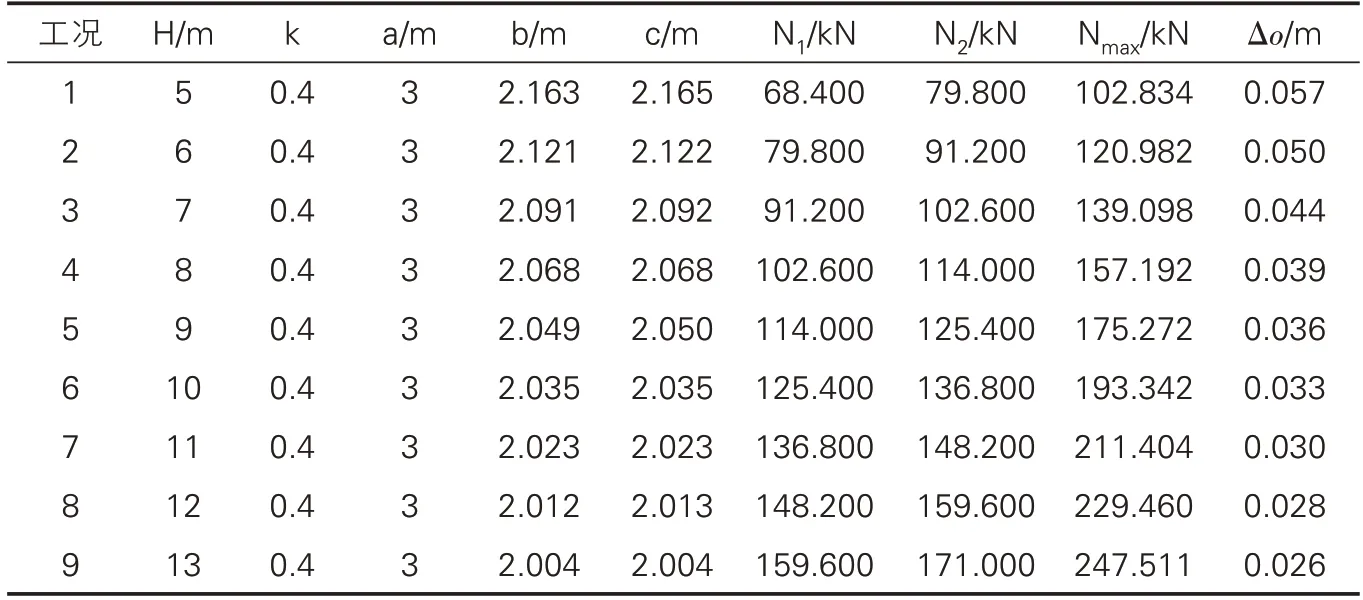
表1 不同顶部理论上覆土厚度时管涵横断面参数及轴力

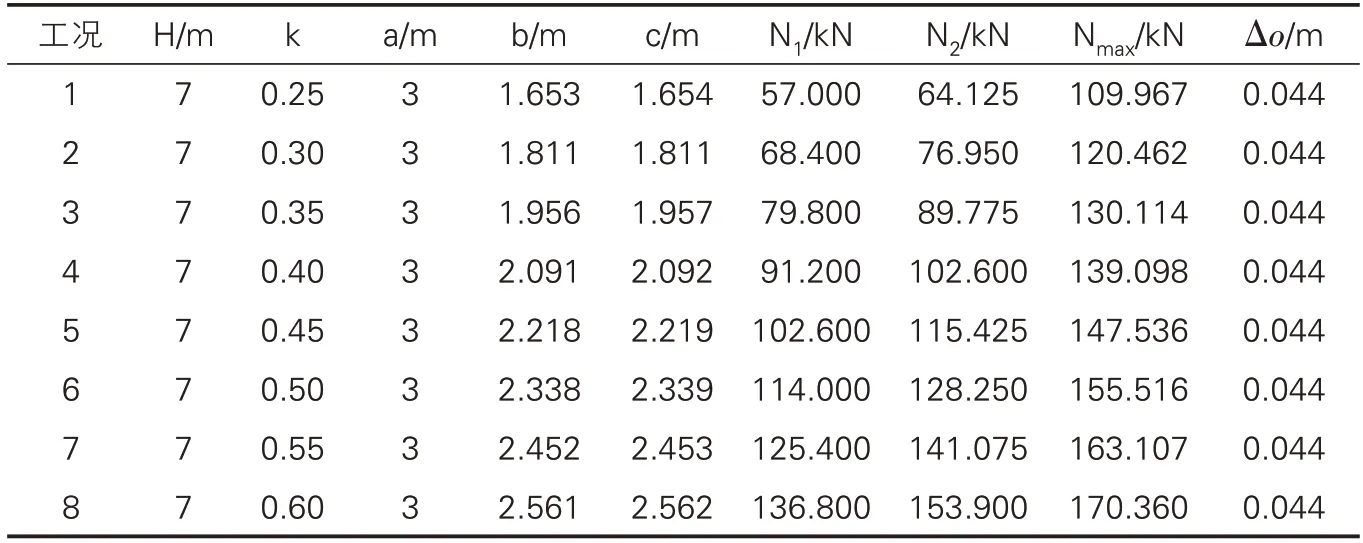
表2 不同侧土压力系数时管涵横断面参数及轴力

内力计算结果表明，在合理受力状态下，任意截面的剪力为零，最小轴力出现在拱顶位置，即为N1，最大轴力出现在与最大水平直径c同高度的侧部位置，即为Nmax。需要说明的是，在此计算的轴力是单位宽度（1m）波纹钢管环的截面轴力。

上述的计算公式与横断面参数表均无法直观地看出零弯矩波纹钢管涵的横断面，为此，将表1 和表2 中各工况的零弯矩波纹钢管涵的横断面作图，如图7所示。从图7(a)中可看出，随着理论上覆土厚度的增加，波纹钢管涵的横断面越来越接近稳定，且任一工况下，零弯矩波纹钢管涵的横断面均与圆形横断相差较大，且同一竖直径的零弯矩波纹钢管涵，在任意工况下水平直径之间的差值，均要小于任意工况下水平直径与同竖直径圆形波纹钢管涵的水平直径之间的差值。由图3与图5的弯矩计算图可知，某工况下的零弯矩波纹钢管涵横断面取为另一工况下的零弯矩波纹钢管涵横断面，管涵的弯矩均要小于圆形横断面波纹钢管涵在同工况下的弯矩，因此，竖向土压力误差对弯矩影响不大。但从图7(b)中可以看出，侧土压力系数k对零弯矩波纹钢管涵的横断面形状影响相对显著，因此，在波纹钢管涵的横断面设计时，需要合理地评估填土的侧土压力系数。在此主要是为了示意出不同侧土压力系数的横断面形状，实际的侧土压力系统变异范围并没有这么大。零弯矩波纹钢管涵的横断面均与圆形横断相差较大，由此可见，为了减小波纹钢管涵的横断面内力与变形，当前的波纹钢管涵的横断面是可以调整的。

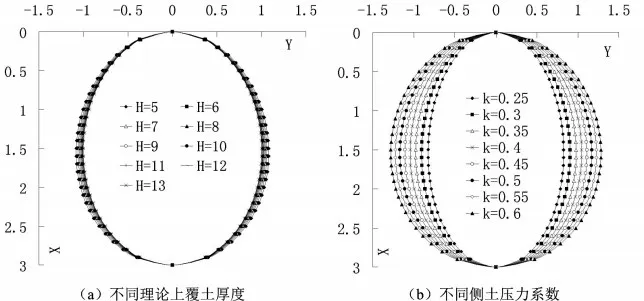
图7 竖直径为3m的零弯矩波纹钢管涵横断面

3 结语

本文通过对波纹钢管涵在零弯矩时的力学模型进行分析，得到了波纹钢管横断面轴线及其内力的计算公式。

对波纹钢管涵的横断面及内力特性进行了分析，结果表明，在合理受力状态下，波纹钢管涵的横断面并不是圆形，而是竖直径大于水平直径的类椭圆结构，且横断面参数与竖向土压力及水平土压力有关；波纹钢管涵横断面剪力为零，轴力在拱顶位置最小，在最大水平直径同高度位置最大。由此可见，当因工程设计所需需要减小波纹钢管涵的横断面内力与变形时，波纹钢管涵的横断面可以进行调整。