基于非球形颗粒水化堆积的水泥浆氯离子扩散系数预测

张坚， 刘清风

（1.浙江农林大学 暨阳学院， 浙江 诸暨 311800； 2.上海交通大学 海洋工程国家实验室， 上海 200240）

钢筋混凝土因性能优越、经济耐用已被广泛应用于工程建设中，但当其处于氯盐环境时，氯离子引发的钢筋锈蚀不容忽视.根据调查发现，中国因钢筋锈蚀导致的经济损失高达国民经济的3.34%［1］.氯离子扩散系数是导致钢筋锈蚀的关键参数［2-5］，如何更加精准和便捷地获取这个参数对混凝土耐久性评估具有重要作用.

在水泥浆微观尺度，水泥颗粒形状会依次作用于水泥浆的水化进程、微观孔结构和氯离子传输行为［6-7］，因而考虑水泥颗粒形状特征带来的影响逐渐受到关注［8］.为了解析水泥颗粒形状对氯离子扩散特性的作用，首先需要建立合理的水泥水化模型.目前重构水泥浆水化模型（即连续基模型［8］）有Hymostruc 3D［9］和μic［10］，这类模型通过存储描述水泥颗粒特征的位置、方向和大小等信息，能以独立于不同特征之间的相对大小来存储和处理不同水泥颗粒的特征信息，且不会对信息加以分辨率限制.然而为了避免在分析不同水化产物接触对水化干扰程度的影响时所引起的复杂数学运算，水泥颗粒形状通常被简化为球形.椭球颗粒作为非球形颗粒的代表，Needle水化模型［11-13］通过采用椭球状水泥颗粒可以很好地显示出实际水化放热特征.基于X射线断层扫描（X-CT）技术对水泥颗粒形状的统计得出长细比是决定水泥颗粒形状的关键参数［14-15］.已有研究将新拌水泥浆构建成由一定长细比的椭球水泥颗粒组成的三维模型［16-17］.根据上述分析，有必要进一步对基于椭球颗粒的水泥浆进行水化动力学模拟，明确长细比对水化度、孔结构特征的影响，以此解析水泥颗粒形状对水泥浆氯离子扩散系数的作用机理.

针对上述问题，本文通过解析水化层相互干扰下的水化演变特征，建立基于椭球颗粒的水泥浆水化模型，以明确长细比对水泥浆水化度、孔径分布和孔隙率的作用；通过综合考虑水泥浆各项组成的扩散特征，提出基于First-passage理论的布朗运动算法用于预测水泥浆中的氯离子扩散系数，随后阐明了长细比对氯离子扩散系数的作用机理.

1 水泥浆水化模型构建

1.1 水化模型

在影响水泥水化的诸多因素中，水泥颗粒形状对水泥水化机理影响的探究尚少［6-7］.已有研究表明，长细比μ是决定实际水泥颗粒形状的关键参数［14-15］，因此，在水化模型中考虑长细比不仅可有效增加水泥浆微结构重构过程的可靠性，还为探讨其对氯离子扩散系数的影响奠定基础.需要指出的是，由于温度参数会显著影响水泥浆微结构演化进程和布朗运动的速度，接下来的水化模型建立和布朗运动算法构建过程均在常温下进行.对于一定长细比的椭球颗粒，根据固体物料的筛分分析可知，其短轴长度D即为粒径.依据Rosin-Ramler函数，椭球水泥颗粒粒径的分布函数P（D）为：

式中：D0、Dm分别为最小、最大水泥颗粒粒径；α、β均为描述水泥颗粒分散程度的参数.

初始椭球水泥颗粒在立方体模拟单元中详细的生成和分布过程见文献［18］.水泥熟料硅酸三钙（C3S）、硅酸二钙（C2S）、铝酸三钙（C3A）和铁铝酸四钙（C4AF）是水泥的主要成分，它们一旦与水接触，便开始发生水化反应.参与反应的水泥体积为f，水化产物的体积fh和耗水体积fw分别为：

式中：k0、k1为体积相互作用常数.

由此，未水化水泥颗粒（UC）、水化水泥颗粒（HC）和空气层的体积分别为：

式中：fuc、fhc、fa分别为未水化水泥颗粒、水化水泥颗粒及空气层的体积；fha为水化水泥颗粒与空气层的体积之和.

在水化模型中，水化水泥颗粒的膨胀和未水化水泥颗粒的收缩均在垂直于前一水化迭代步骤的水化颗粒和未水化颗粒的表面进行，当椭球水泥颗粒以均匀厚度覆盖或去除时，改变后的外轮廓不再是椭球体，导致其表面方程比球体复杂得多.不仅如此，椭球体上的点接近或位于其短轴与曲面的交点，该点处法向向量的斜率达到无穷大.基于上述原因，纯解析的表面表达式很难直接获得，由此引入了数值方法求解未水化和水化水泥颗粒的表面方程.

式中：Ph为水化水泥颗粒中各层的表面方程；PE为椭球水泥颗粒的参数方程；δ为初始水泥颗粒轮廓的厚度；γ和fp为参数方程；Da、Db分别为椭球的长轴和短轴长度；ϕ为椭球面上一点和球心o点的连线与平面xoy的夹角.

根据δ<0，φ的范围为［ϕ1，ϕ2］∪［ϕ3，ϕ4］，其中ϕi（i=1、2、3、4）表示γ（ϕ）=0或π的解.基于上述方法，椭球水泥颗粒的水化模型见图1（图中IH、OH分别为水泥颗粒的内水化层、外水化层）.

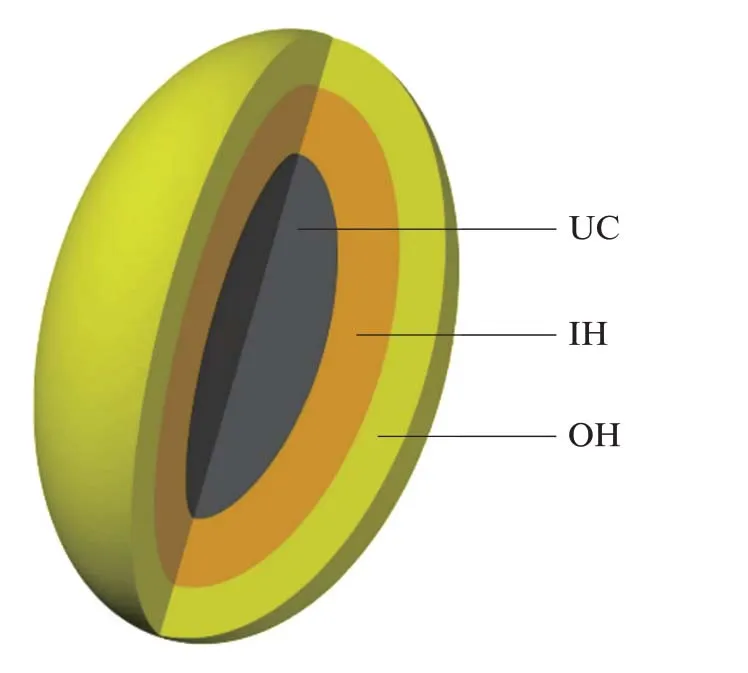
图1 椭球水泥颗粒的水化模型Fig.1 Hydration model of ellipsoidal cement particle

由于水化第一阶段反应机理复杂，且该阶段仅在水化的初始阶段（水化程度小于2%时）起主导作用，因此相对于整个水化过程，其持续时间可忽略不计.对于水化反应中的相边界和扩散阶段，未水化水泥颗粒的反应速率可表示为：

式中：δin（t）为t时刻未水化水泥颗粒的厚度；K0为反应速率常数；δtr为临界水化层厚度；δh（t）为t时刻水化层的厚度；H（x）为阶跃函数.

在构建的新拌水泥浆模拟单元中，最初分布的水泥颗粒彼此不接触，但随着水化反应的进行，水化凝胶产物不断生成，水化层和空气层的厚度不断增加，导致越来越多的水化水泥颗粒相互接触，阻碍水分和离子（Ca2+、OH-和Si4+等）的正常运输，从而影响整个水化过程.为了量化这种水化干扰效应，分别引入水化产物的干扰程度ω1（t）、未水化水泥颗粒的干扰程度ω2（t）、空气层的干扰程度ω3（t）来评价：

式中：N为选自外水化层、未水化层和空气层的随机点数；Ni（t）为t时刻位于非接触表面上的点数.

当考虑ω1（t）、ω2（t）、ω3（t）时，t时刻未水化层厚度径向的减少量rin（t）、δh（t）和空气层的厚度δair（t）可改写成：

式中：δout为t时刻外水化层的厚度；fc为描述外水化层和空气层轮廓的函数.

最后，通过将所有未水化水泥颗粒的体积fuc，i相加，可得到模拟单元中未水化的水泥颗粒体积，由此确定水泥水化度αc为：

式中：fc为初始椭球水泥颗粒的总体积.

1.2 水化模型验证和孔结构分析

为验证水化模型的可靠性，选取文献中的试验数据［19］进行比较.根据试验信息，在数值分析中，水灰比mW/mC（质量比，文中涉及的含量、比值等除特殊说明外均为质量分数或质量比）为0.4、0.5，水泥颗粒粒径为1～26 μm，水泥中C3S、C2S、C3A、C4AF的含量分别为60%、25%、8%、7%，水泥浆立方体模拟单元的边长l为65 μm，实际水泥颗粒的平均长细比μ为1.46［20］.水泥浆微观结构重构及水化模型的验证分别见图2、3.由图3可见：计算结果与试验数据吻合良好；当mW/mC为 0.4、0.5时，两者的相关系数分别为0.97、0.98.因此，水化模型的可靠性得到了验证.

图2 水泥浆微观结构重构Fig.2 Reconstruction of microstructure of cement paste

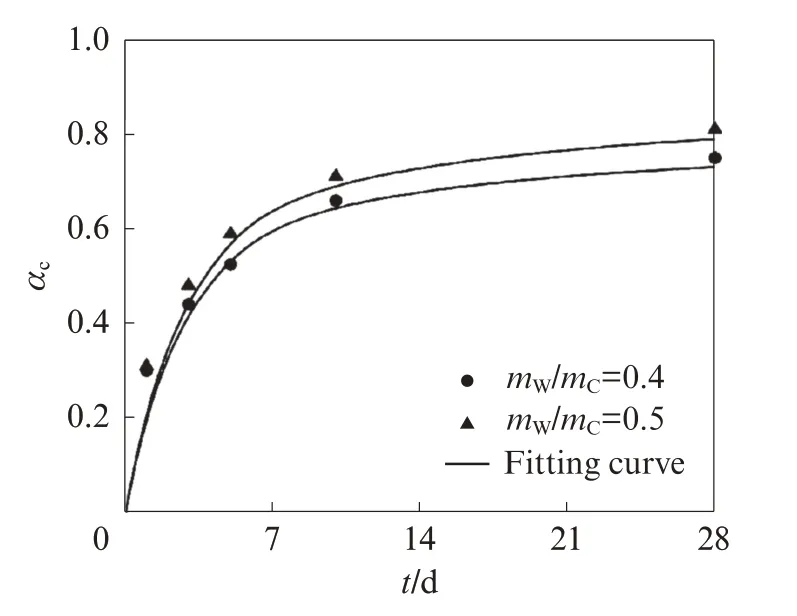
图3 水化模型的验证Fig.3 Verification of hydration model

利用水化模型评价了mW/mC=0.5时水泥颗粒长细比对水化度的影响，结果见图4.由图4可见，αc随着μ的增大而减少，当t=7、14、28 d，μ从1.00增大至3.00时，αc分别下降了17.5%、13.1%、8.9%.这主要是由于椭球水泥颗粒的长细比越大，其比表面积越小，水化速率取决于水泥表面与自由水的接触程度，因此比表面积越大，水化速率越快，尤其表现在水化初期.需要注意的是，如若使用等效粒径的概念［21］，球的比表面积小于椭球，椭球形水泥颗粒的水化程度会更高.

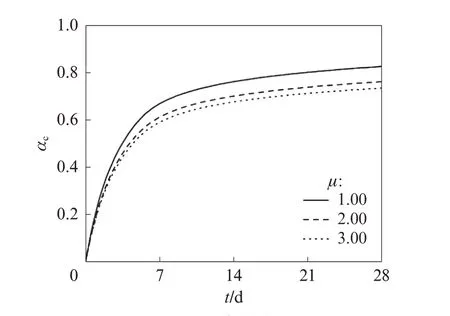
图4 长细比对水化度的影响Fig.4 Influence of μ on αc（mW/mC＝0.5）

水泥基材料的离子传输性能与其孔结构特征（如孔径分布、平均孔径、峰值孔径、孔隙连通率和孔隙率等）密切相关，通过分析水泥颗粒形状影响下水泥浆的孔结构变化规律，可为阐明长细比对扩散系数的作用机理提供可靠依据.利用三维内侵蚀法［21］对水泥浆中不同尺寸的孔隙分布进行分析，计算得到mW/mC＝0.5时水泥颗粒长细比对孔径分布特征的影响，结果见图5.由图5可见：随着水泥颗粒长细比的增大，水泥浆微结构中出现孔径分布范围左移、小孔体积占比增加和平均孔径减小的趋势 ；随着孔隙率的减小（即龄期增加），长细比的这种影响效应会增强.这不仅解释了“长细比越大，扩散系数就越小”的变化规律，而且揭示了28 d后长细比对扩散系数影响的增益效应.

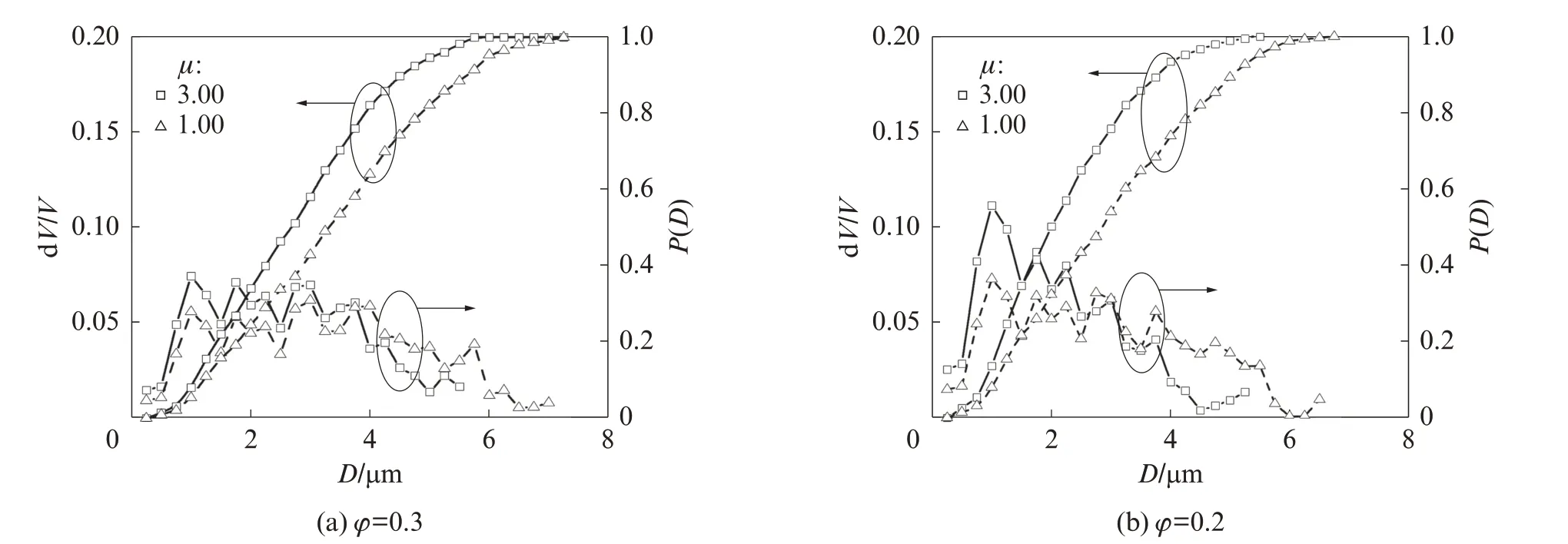
图5 长细比对孔径分布特征的影响Fig.5 Influence of μ on distribution features of pore diameter（mW/mC=0.5）

长细比对孔隙率的影响见图6.由图6可见：水泥浆孔隙率随着t的增长而减小，这是因为随着水化进程的进行，水化产物不断填充水泥浆的毛细孔（CAP），从而导致水泥浆孔隙率不断降低；水泥浆孔隙率随着μ的增大而增大，这是因为孔隙率的大小依赖于水化程度，水化程度越小孔隙率越大，水化程度会随着长细比的增大而减小，从而导致孔隙率随着μ的增大而增大.

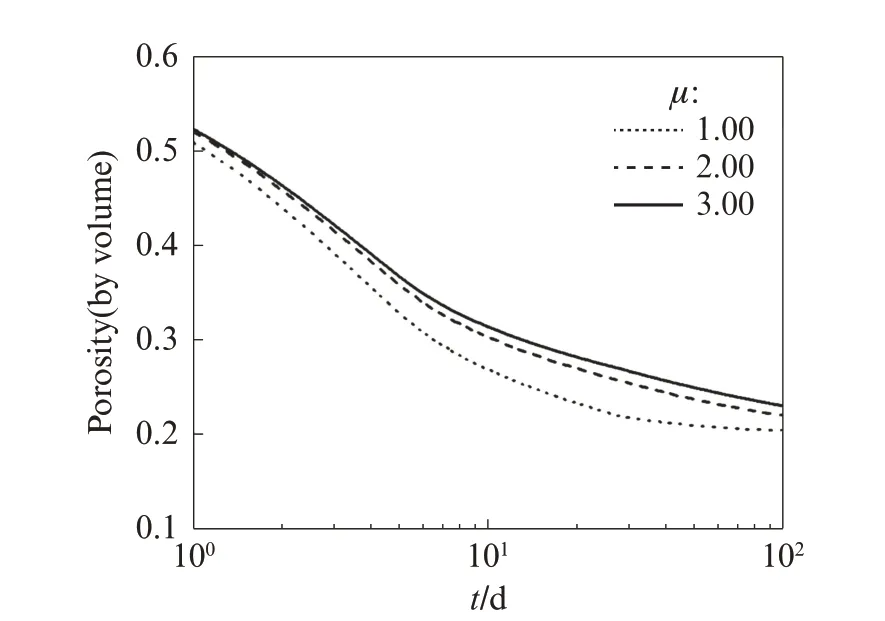
图6 长细比对孔隙率的影响Fig.6 Influence of μ on porosity

2 氯离子扩散系数预测

2.1 布朗运动算法构建

在宏观尺度上，氯离子在水泥浆中的扩散可描述为浓度梯度作用下氯离子从高浓度区域向低浓度区域运输的过程.从微观尺度上看，氯离子扩散则被视为众多氯离子在水泥浆中作布朗运动后的统计结果［18-19］.因此，本节将基于上述重构的水泥浆水化模型，构建一种适用于多相多孔介质材料的布朗运动算法，并用于计算水泥浆中的氯离子扩散系数.基于First-passage理论，在由多相组成的水泥浆体中，本算法将布朗粒子（即氯离子）的运动形式分为2类，即在单一相（如CAP、IH、OH和UC）中和两相交界处做锯齿形运动.需要特别指出的是，当氯离子在几十纳米及以上的毛细孔中做布朗运动时，其自身尺寸对传输的影响可以忽略不计；另外，由于水化层中的凝胶孔尺度较毛细孔要小一层级，当离子在水化层中运动时，对水化层组成相（包括凝胶孔、高或低密度水化硅酸钙（HD C-S-H或LD C-S-H）、氢氧化钙（CH）和少量钙矾石（AFt））的传输特性一般进行均一化处理，以避免尺度跳跃导致计算机运算效率过低［19，22］.对于第1类运动（见图7（a）），当位于O处的布朗粒子距两相交接面的最小球形相切距离ri大于等于其在单一相中运动或两相交接面处运动的最小临界距离rs时，其运动的时间ti为［18］：

图7 布朗粒子的运动形式Fig.7 Motion patterns of Brownian particles

式中：D（i）为当前布朗粒子位置处的扩散系数.

对于第2类运动（见图7（b）），即ri

式中：ε为两相扩散系数的比值；V1、V2分别为球形跳转表面被两相交界面划分成的两部分的体积；rs、rj一般分别取0.001、0.050 μm.

基于设定的运动规则，当布朗粒子第1次通过半径为R的球面时，布朗粒子的总运动时间t由以下两部分相加：

最后，水泥浆中的氯离子扩散系数Dcp为：

根据本文建立的布朗运动算法，通过记录单个布朗粒子在模拟单元中运动的时间和距离，可根据式（21）计算氯离子扩散系数.布朗粒子数M和位移R这2个参数都会影响最后氯离子扩散系数的收敛性，因为单次计算得到的结果并不能反映模拟单元的扩散性能，只有当布朗粒子数M逐渐增大时，氯离子扩散系数才会趋于稳定.R对扩散系数具有同样的作用.为了兼顾计算精度和计算机运行速率的要求，通过敏感性分析找到合适的R和M值显得非常重要.在敏感性分析中：水泥颗粒粒径为1～26 μm；水泥中C3S、C2S、C3A、C4AF的含量分别为60%、25%、8%、7%；l=60 μm；mW/mC=0.4；μ=1.46.在氯离子传输模型中，各相扩散系数一般取为定值，即毛细孔溶液的氯离子扩散系数Dcap、未水化水泥颗粒的氯离子扩散系数Duc、内水化层的氯离子扩散系数Dih和外水化层的的氯离子扩散系数Doh分别为1.07×10-10、0、0.83×10-12、3.4×10-12m2/s［19，22］.计算得到的Dcp与R、M的关系见图8.由图8可见，当R≥ 80 μm、M≥ 400时，Dcp趋于稳定.综上，下文计算中R和M的取值分别为80 μm和400.

图8 Dcp与R、M的关系Fig.8 Relationship between Dcp and R，M

当R=80 μm时，通过引入布朗运动的周期性边界条件［19］，布朗粒子依据已经建立的运动规则在模拟单元中沿某一路径运动，结果见图9.图9（a）为水化时间28 d时基于椭球水泥颗粒的水泥浆立方体单元，模拟单元尺寸为60 μm，图中浅蓝色区域表示毛细孔.由图9（b）可见，布朗粒子的运动路径贯穿了模拟单元的4个面（x=0、60.0 μm、z=0、60.0 μm），相应贯穿点的坐标可见图中的标记.这说明布朗粒子运动路径分布覆盖了模拟单元的大部分区域，根据R=80 μm的单次布朗运动路径得到的扩散系数可初步反应整个模拟单元的扩散特性，一旦粒子数M达到400时，模拟单元的氯离子扩散系数便会收敛于固定值.

图9 水泥立方单元和布朗粒子的运动路径Fig.9 Microstructure model of cement paste and motion path of Brownian particles

2.2 验证与讨论

为了验证布朗运动算法的可靠性，选取文献中的试验数据［19］进行比较，结果见图10.根据试验信息，数值计算中的mW/mC为 0.3、0.4、0.5，水泥颗粒粒径为1～26 μm，水泥中C3S、C2S、C3A、C4AF的含量分别为62%、24%、8%、6%，其余参数的取值同2.1中敏感度分析.

图10 计算值与试验值的比较Fig.10 Comparison of numerical results and test data

由图10可见：计算值和试验值吻合良好；当mW/mC为0.3、0.4、0.5时，两者的相关系数分别达到了0.96、0.96、0.97.综上，氯离子扩散系数预测方法的有效性得到了证实，将在接下来的讨论和参数分析部分予以应用.

由图10还发现，Dcp与mW/mC、t密切相关.Dcp随着mW/mC的增大而显著增大，当t为28、120、360 d时，mW/mC=0.5的水泥浆Dcp值相比于mW/mC=0.3时分别增大了264.0%、344.0%、393.0%.其主要原因是毛细孔连通率会随着mW/mC的增大而迅速增加，此过程毛细孔逐渐成为氯离子传输的主要通道，而毛细孔扩散系数是外水化层的31.5倍.Dcp随着t的增长而逐渐减小，当mW/mC为0.4、0.5、0.6时，t=120 d的水泥浆Dcp比t=28 d时分别减小了23.0%、28.0%、37.0%，t=360 d的Dcp比t=120 d时分别减小了10.0%、11.0%、15.0%.从数据分析可见，当t>120 d时，随着t的增长，Dcp递减率降低.这是因为水泥的水化进程在120 d内基本完成，此过程的水泥浆孔隙率会大幅减小，而后水泥水化度和孔隙率均几乎不变.

3 参数的敏感性分析

长细比是表征实际水泥颗粒形状的关键参数［14-15］，其对水泥水化进程和水泥浆微结构均存在影响，且已在1.2中进行了定量分析.为了进一步实现水泥颗粒形貌特征对氯离子扩散系数的参数化分析，本节将基于重构的水泥浆水化模型和布朗运动算法，讨论长细比对氯离子扩散系数的作用.在参数设置中，根据X-CT探测的结果得出，实际水泥颗粒的长细比通常在1～3范围内［14］，因此μ取1.00、2.00、3.00.其余参数取值同2.1中敏感度分析.

当mW/mC=0.5时，长细比对氯离子扩散系数的影响见图11.由图11可见：当t为1、10、28、100 d，μ从1.00增至3.00时，Dcp分别减少了23.8%、0.5%、7.8%、22.1%，即μ对Dcp的作用随着t的增大而逐渐减小，而后又逐渐增大.其主要原因为在水化早期，水泥颗粒的向外生长程度还不明显，水泥颗粒间尚未形成相互连结的团聚体，使整个孔隙网络的迂曲度未被明显干预.在这种情况下，尽管μ=1.00的水泥浆孔隙率小于μ=3.00的水泥浆，但该阶段长细比对氯离子扩散系数的影响大于孔隙率.由于氯离子扩散系数会随着长细比的增大而减小［18］，从而出现μ越大Dcp越小的现象.当t从1 d往28 d过渡时，水泥颗粒之间逐渐开始连结，孔隙率减小引起水泥浆迂曲度增大的效应开始比长细比的影响更明显，这解释了μ对Dcp的作用随着t的增大而减小.当t>28 d时，μ=1.00和μ=3.00的水泥浆孔隙迂曲度比较接近，长细比对氯离子扩散系数的影响又开始凸显.

图11 长细比对氯离子扩散系数的影响Fig.11 Influence of μ on Dcp

4 结论

（1）建立了基于椭球水泥颗粒水化堆积的水泥浆水化模型，通过第三方试验数据，验证了水化模型的可靠性.通过分析椭球颗粒长细比对水化度、孔径分布和孔隙率的影响发现，随着水泥颗粒长细比μ的增大，水泥浆水化度减小而孔隙率增大；此外，水泥浆微结构中出现孔径分布范围左移、小孔体积占比增加和平均孔径减小的趋势，当孔隙率减小（即龄期增加）时，长细比的这种影响效应会增强.

（2）基于First-passage理论，建立了综合考虑各水泥浆组成相时的布朗运动算法，用于预测水泥浆中的氯离子扩散系数Dcp，通过对比试验结果验证了该算法的可靠性.为兼顾求解氯离子扩散系数过程中计算机的运算速率和计算精度，通过敏感性分析获得了氯离子扩散系数收敛时的布朗粒子数和位移.

（3）基于建立的水泥浆水化模型和布朗运动算法，得到了μ对Dcp的作用随水化时间t的演变规律.通过数据分析发现，μ对Dcp的作用随着t的增大而逐渐减小，而后又逐渐增大.当t从10 d往28 d过渡时，μ对Dcp几乎没有影响；但当t超过28 d时，长细比对氯离子扩散系数的影响又开始显著.综上，在考虑水化全过程的水泥浆微结构演化及其氯离子传输中，长细比的影响不容忽视.