物理冶金信息指导机器学习的镍基单晶高温合金蠕变寿命预测

付佳博，王晨充，MATEO Carlos Gracia，CARABALLO Isaac Toda,CABALLERO Francisca Garcia，于 皓

(1.东北大学 轧制技术及连轧自动化国家重点实验室，辽宁 沈阳 110819) (2.西班牙国家冶金研究中心物理冶金系，西班牙 马德里 28040)

1 前 言

镍基单晶高温合金作为航空发动机涡轮叶片的关键材料，具备优异的承温性能和抗蠕变性能[1]。然而在抗蠕变性能的研究中，讨论最多的是高温低应力条件下的蠕变，这与镍基单晶高温合金涡轮叶片在实际应用中的情况相契合[2，3]。因此，提高新一代镍基单晶高温合金在高温和低应力下的蠕变寿命是合金设计的主要目标之一。

镍基单晶高温合金由于涉及大量昂贵的金属元素、单晶制造技术成本高、蠕变试验周期长，同时缺乏成分、组织和性能之间的定量关系，通过传统的试错法来提高合金的蠕变抗力需要耗费大量的时间和成本。因此，如何加速预测镍基单晶高温合金的蠕变寿命具有重要意义。传统预测蠕变寿命的方法主要分为外推法和蠕变本构模型两种。外推法一般根据短期数据寻求经验公式，用以计算外推长期结果，或者是根据高温蠕变与蠕变断裂的微观过程，建立起温度、应力、蠕变速率或蠕变断裂时间之间的关系式[4，5]。但是这种方法没有充分考虑实际蠕变过程中的显微组织演化信息，缺乏严谨的理论基础。蠕变本构模型则是基于蠕变过程中的组织演化信息，从微观角度出发建模预测合金的蠕变行为。Zhu等[6]通过考虑析出物的形态、尺寸和间距等几何结构因素，认为蠕变速率取决于γ/γ′界面处位错的滑移和攀移以及从俘获组态中逃逸的速率，提出了一种对化学成分和显微组织敏感的镍基单晶高温合金蠕变变形行为模型。Reed等[7，8]则是考虑高温下的位错攀移绕过蠕变机制，基于控制位错蠕变和空位辅助扩散的原子尺度过程的预期相似性，通过计算有效扩散系数来评估合金的蠕变抗力。Kim等[9]通过对已有模型的修正和组合，描述了将理论模型与相图计算(CALPHAD)方法相结合的高通量计算，建立了基于组织、工艺和蠕变条件以及材料性能的数学模型，并将该模型用于预测镍基高温合金中温区蠕变性能。虽然相关学者已经对如何加速预测镍基单晶高温合金的蠕变寿命进行了大量的研究，这些理论方法能够准确地描述合金的蠕变过程，并能在较短的时间内成功地预测合金的蠕变断裂寿命，但是由于镍基单晶高温合金的蠕变过程涉及长时间的显微组织演化，并且在不同温度应力下蠕变机制有所不同。因此想要进一步提升模型的准确性和适用性是非常困难的。

近年来，随着人工智能的快速发展，机器学习算法在建立高通量数据关联方面具有极大的优越性，已被越来越多地应用于材料性能的预测。Han等[10]基于从文献中收集的小数据集，通过数据驱动的机器学习方法，开发了一种基于双模型联动的方法来预测合金的蠕变寿命。基于高精度模型来判断和调整低精度模型，最终成功改善了整体蠕变寿命预测的精度。然而该方法仅考虑了成分参数和测试条件，并没有进一步考虑工艺参数和物理冶金参数对镍基单晶高温合金蠕变寿命的影响，缺乏可解释性。Liu等[11]在考虑化学成分、测试温度、测试应力和热处理工艺的基础上，同时基于相图计算方法和各种基本材料结构-性质关系计算并引入了层错能、晶格参数、γ′相的摩尔分数、扩散系数和剪切模量5个物理冶金参数，基于聚类方法区分混合蠕变机制，为每个类别训练出一个最优模型，大大提高了机器学习模型的预测能力。但是需要指出的是，该方法虽然能够区分不同的蠕变机制并分别建立机器学习模型，但对于不同蠕变条件的形变机制(如图1所示)，此工作并未考虑引入不同的物理冶金参数来指导机器学习模型，如层错能和剪切模量对应中低温蠕变机制[12，13]并不适用于高温蠕变机制，这可能会恶化基于单一蠕变机制建立的机器学习模型的预测准确性和可解释性。

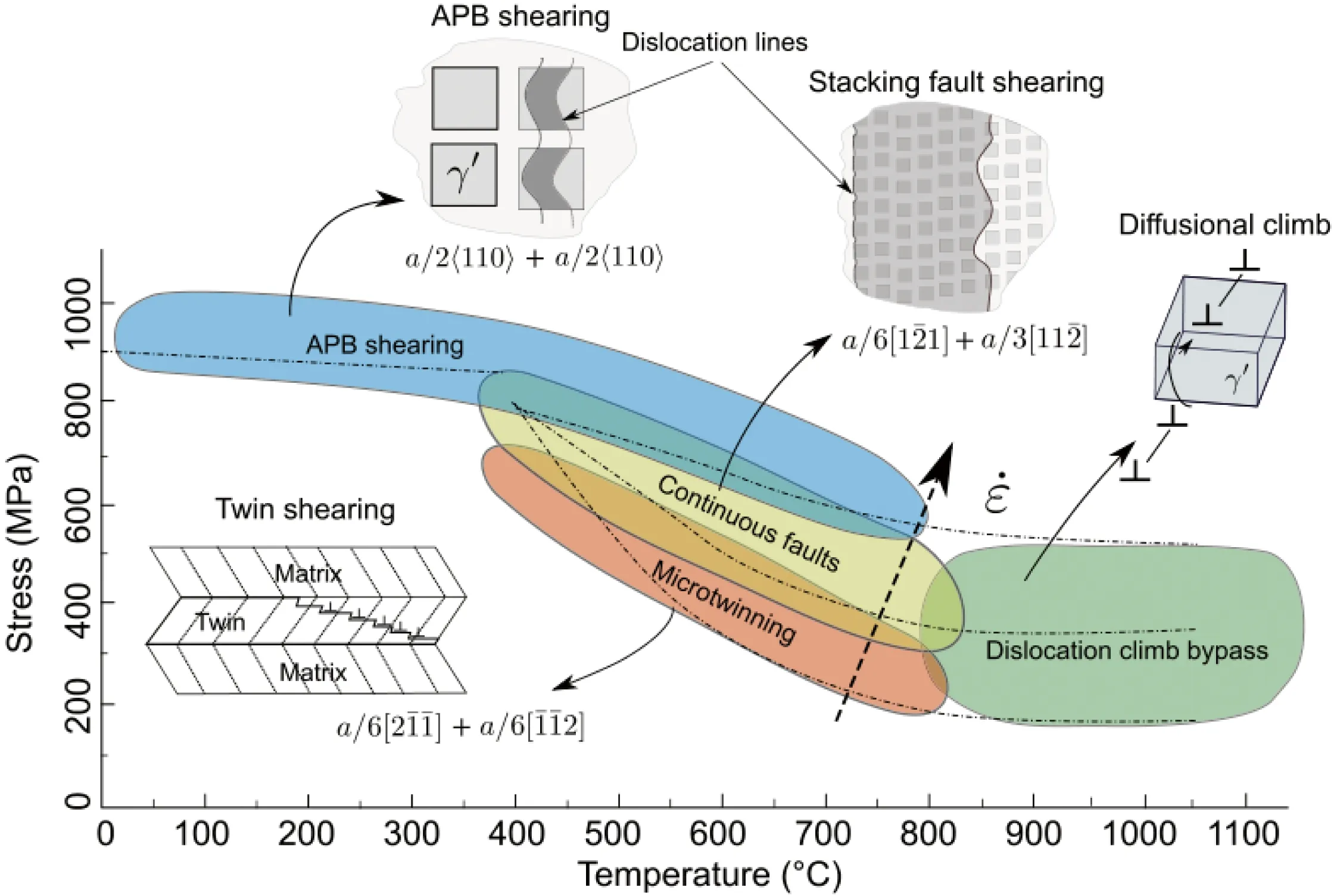
图1 单晶高温合金在不同服役温度及应力范围内的蠕变变形机制示意图[12，13]Fig.1 Deformation map for a single crystal superalloy illustrating the dependence on stress，temperature and strain rate[12，13]

综上所述，人工智能分析策略对于高温合金材料蠕变性能的预测颇有成效，但是目前所建立的机器学习模型没有考虑符合高温低应力蠕变机制的物理冶金参数，不能够对高温低应力条件下镍基单晶高温合金的蠕变性能实现准确预测。对此，本文的研究目的在于通过人工智能算法，建立起高温低应力下镍基单晶高温合金成分、工艺以及引入的物理冶金参数和蠕变寿命之间的关系，最终能够有效地预测蠕变寿命，有望应用于合金成分工艺的反向设计。

2 实验方法

2.1 数据库的建立

本数据库的文献信息部分来源于Liu等[11]的研究，基于数据质量分析保留122条高温低应力下的蠕变数据。此外基于文献调研[14-37]，收集镍基单晶高温合金的蠕变数据合计110条。最终建立了较高质量的镍基单晶合金蠕变数据集(成分/工艺/测试条件-蠕变寿命)。

如表1所示，数据集中包括23个输入特征和1个输出特征(蠕变寿命)。数据集的输入特征，综合考虑了材料特性和环境因素。材料特性包括15个元素(Ni，Cr，Mo，W，Co，Re，Ru，Al，Ti，Ta，Hf，C，B，Nb，Y)含量特征和6个工艺参数(固溶温度(ST)和时间(St)、一次时效温度(1aT)和时间(1at)、二次时效温度(2aT)和时间(2at))。环境因素则包括与蠕变过程密切相关的蠕变温度(tT)和蠕变应力(tS)。

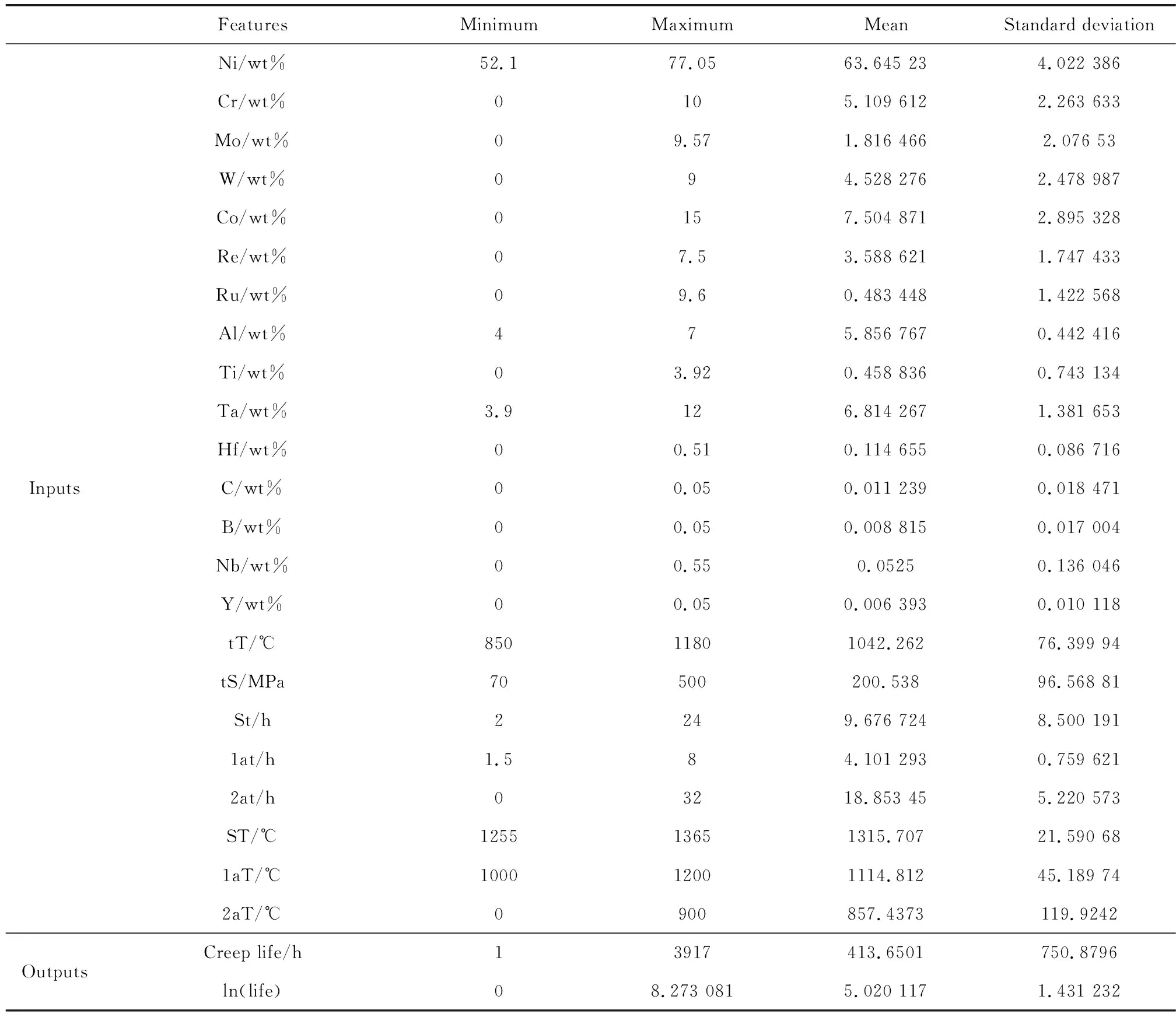
表1 镍基单晶高温合金蠕变数据特征的基本信息Table 1 Basic information of the features in the creep dataset of Ni-based single crystal superalloy

2.2 物理冶金参数的引入

对于基于机器学习回归策略的性能预测，引入物理冶金变量可以有效地提高泛化能力，而对于设计过程，可以消除不符合物理冶金原则的中间解，从而提高设计的精度和效率[38]。由于镍基单晶高温合金在高温和低应力下，热激活攀移绕过是主要的变形机制，此时的蠕变变形主要来自于位错在γ基体相中的滑移和沿γ/γ′界面的攀移，与筏状结构的形成有关。因此基于这一蠕变机制，对于镍基单晶高温合金的抗蠕变性能预测，最终考虑引入以下微观结构参数作为模型输入：γ′相体积分数Vf，晶格错配度δ，扩散系数DL，如表2所示。

表2 基于Thermo-Calc计算引入的三维物理冶金信息Table 2 Three-dimensional physical metallurgical information based on Thermo-Calc calculation

γ′相作为镍基单晶高温合金的主要强化相，其数量、形态、尺寸和分布与合金的力学性能以及蠕变性能是密切相关的[39]。本工作中基于CALPHAD方法中的Thermo-Calc来计算获得服役温度下的γ′相体积分数，作为模型的输入。

在高温合金中，γ和γ′相间的晶格错配度会对界面处位错网络的密度和演化速率以及蠕变断裂寿命产生重要的影响[40，41]。考虑到计算获得服役温度下晶格参数的公式过于依赖经验，因此在本研究中只采取室温下的晶格错配度[42]作为输入，如式(1)～式(3)：

(1)

(2)

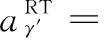
(3)

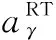
在高温低应力下，原子扩散机制是合金发生蠕变变形的重要原因之一，原子的扩散会影响蠕变发生的速率、γ′相的粗化以及扩散控制的氧化速率。在Zhu等[6]的研究中将γ相的晶格扩散系数作为其高温蠕变模型中的有效扩散系数，这其实是一种简化计算扩散系数的方法，特别是对扩散系数以复杂基体形式存在的多元体系的镍基单晶高温合金而言。通过进一步数学上的推导简化，本研究中采取式(4)进行扩散系数的计算：

(4)

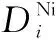
2.3 建模过程

本研究基于人工智能策略建立蠕变寿命的最优预测模型的基本流程如图2所示。在建立了数据库并且引入了物理冶金参数之后，首先对数据进行预处理，基于归一化处理将原始的数据特征去量纲化并缩放至相同的尺度，如式(5)所示：

图2 蠕变寿命最优预测模型建立的基本流程Fig.2 The basic flow of establishing the optimal prediction model of creep life

(5)

基于Pearson系数和随机森林平均精确度降低(MDA)值等数据关联性分析方法评估数据特征之间的关联性以及重要性。选择7种经典的机器学习算法建立性能预测模型，包括线性回归(LR)、支持向量回归(SVR)、多层感知机(MLP)、随机森林(RF)、梯度提升回归(GBR)、极端梯度提升回归(XGB)和自适应提升回归(AdB)模型，训练模型之前需要将数据集按照8∶2的比例划分为训练集和测试集，建模过程中基于网格搜索法调参，训练并优化机器学习模型。最后基于平方相关系数(R2)和平均绝对误差(MAE)评估模型性能，分别如式(6)和式(7)所示：

R2=

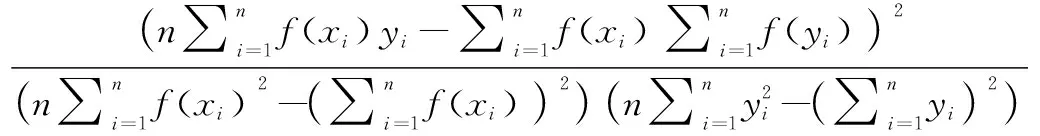
(6)

(7)

3 结果和讨论

3.1 特征分析

对数据集进行了Pearson系数相关性分析(如图3所示)：任意两个特征之间Pearson系数的绝对值均小于1，这说明所有的特征均可以视为独立变量。每个特征相对于输出变量的Pearson系数的绝对值均大于0，这意味着每个特征对于蠕变寿命都有自己的贡献。因此，单独分析各特征对蠕变寿命的重要性是合理的。

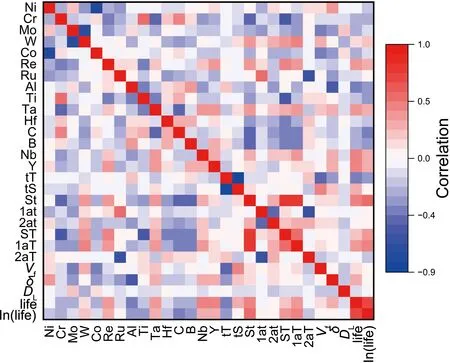
图3 Pearson系数热力图Fig.3 Heat map of the Pearson correlation coefficient

图4a定量地显示了基于平均精确度降低值评估的每个特征对蠕变寿命预测的重要性。值得注意的是，引入的3个物理冶金变量Vf、δ、DL的重要性均位于前列，这意味着本研究中引入的3个物理冶金参数对于镍基单晶高温合金蠕变寿命的预测有着重要意义，同时这与高温低应力下位错攀移绕过机制基本吻合，表明本研究所建立的数据集基本符合物理冶金原理。二次时效温度的平均精确度降低值较高，这意味着所收集数据的热处理工艺中二次时效温度极大地影响着合金的蠕变寿命，根据传统的物理冶金理论，二次时效过程影响着γ′相的形貌和尺寸，进而影响着γ基体相和γ′相的晶格错配度，是影响蠕变过程中γ′相能否定向粗化(筏化)的关键因素。此外，测试条件和测试应力的平均精确度降低值位于前列，这说明环境因素对合金蠕变寿命的影响较为重要。同时可以看到γ基体相元素Ni、γ′相形成元素Al和Ta以及固溶强化元素Cr和Re的平均精确度降低值均位于前列，这说明所建立的数据集中成分特征影响同样显著，因为蠕变过程时间较长，涉及显微组织的演化，这与合金元素的扩散过程密切相关，这进一步证明了本研究中所使用的数据集具有一定的可信度和可解释性。

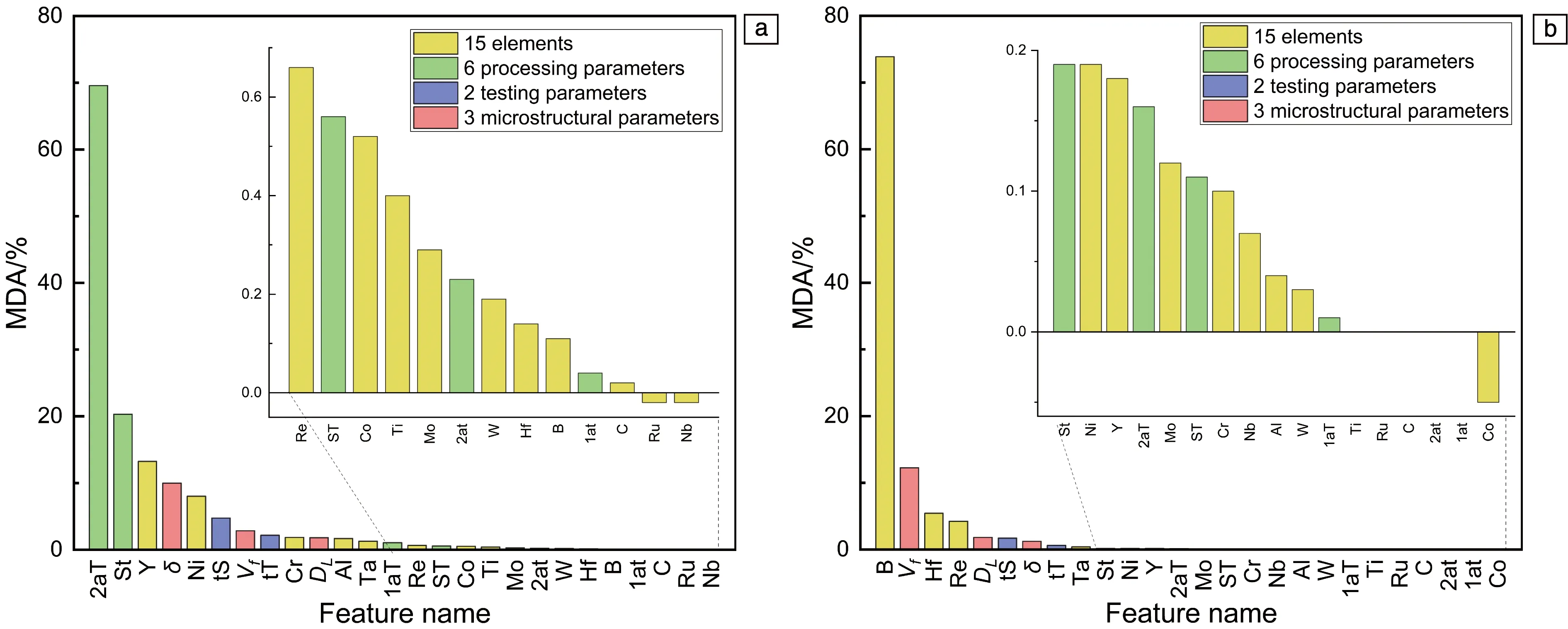
图4 特征重要性评估结果：(a)原始数据特征平均精确度降低(MDA)值，(b)含有Y元素数据集中的MDA值Fig.4 Feature importance evaluation results：(a)the mean decrease accuracy (MDA)value of original data feature，(b)the MDA value of each feature in the dataset containing Y element

平均精确度降低值低估了Ru元素对蠕变寿命的贡献，这是因为作为最新一代镍基单晶高温合金，所能收集到的数据中含Ru元素的样本仅有32个。不可否认的是Ru元素的添加会抑制拓扑密排(TCP)相的析出但同时增加了成本，因此不少学者[18，19，26]致力于追寻调控其他固溶强化元素如Co，Mo和Cr的含量来降低或者替代Ru元素以期降低成本，这意味着基于所建立的数据集通过机器学习算法有希望为高性能低Ru或无Ru单晶高温合金成分工艺的反向设计服务。

不难发现，平均精确度降低值高估了Y元素的贡献，因此后续基于Y元素的有无将数据集分成了两类，评估了有Y元素数据集中的特征重要性。如图4b所示，含有Y元素的数据集中Y元素的特征重要性评估排名非常靠后，这也就表明高估Y元素的原因是数据集中Y元素分布不均匀。

3.2 机器学习算法的选择

在建立稳定的蠕变预测模型之前，将归一化后的数据全部打乱并进行随机划分，将其中的80%用作训练集，余下的20%用作测试集，共进行了100次计算。通过评估100次随机划分训练后的R2和平均绝对误差，对各种机器学习模型的性能进行了比较分析，图5显示了这些模型的R2和平均绝对误差。

从图5a中可以发现，LR模型和AdB模型训练集和测试集的R2值相对较低，而大多数其他模型的R2表现远远好于LR和AdB模型。值得注意的是，虽然RF模型的训练集具有较高的R2值(95%以上)，但是在测试集上表现确不尽人意(80%以下)，这意味着RF在本研究中具有很强的过拟合趋势。这也表明具有26个输入特征的蠕变寿命预测是一个比较复杂的问题，远远超出了RF模型的最大分析能力。同样地，SVR模型、MLP模型、GBR模型和XGB模型4种机器学习算法在训练集上均有良好的表现，R2均在95%以上；然而在测试集上并没有保持这种优异的性能，R2的值集中在80%～90%之间。SVR模型在训练集上的R2达到了96.88%；在测试集上的R2相对较高，达到了87.17%，并且拥有较窄的误差范围。这意味着与其他模型相比，SVR模型更加稳定，过拟合的风险更低。这一结论也可以从平均绝对误差结果中得到证明，如图5b所示，SVR模型在训练集和测试集上的平均绝对误差值分别为0.1689和0.3542，并且误差范围相对较窄。

由于在小样本问题上，机器学习模型的过度拟合是一个重要的风险。因此，为了进一步评估SVR、MLP、GBR和XGB这4种算法的性能，需要对模型的过拟合程度进行评估分析，图6给出了在100次随机划分训练后，训练集和测试集R2差在10%～20%、20%～30%和>30%范围内，SVR、MLP、GBR和XGB这4种算法的过拟合模型的确切个数。由图6可以清晰地看到，相比MLP、GBR和XGB算法，SVR算法的过拟合模型的个数是最少的，这意味着SVR模型拥有最小的过拟合风险。因此，最终选择SVR作为镍基单晶高温合金高温低应力条件下蠕变寿命预测的模型。

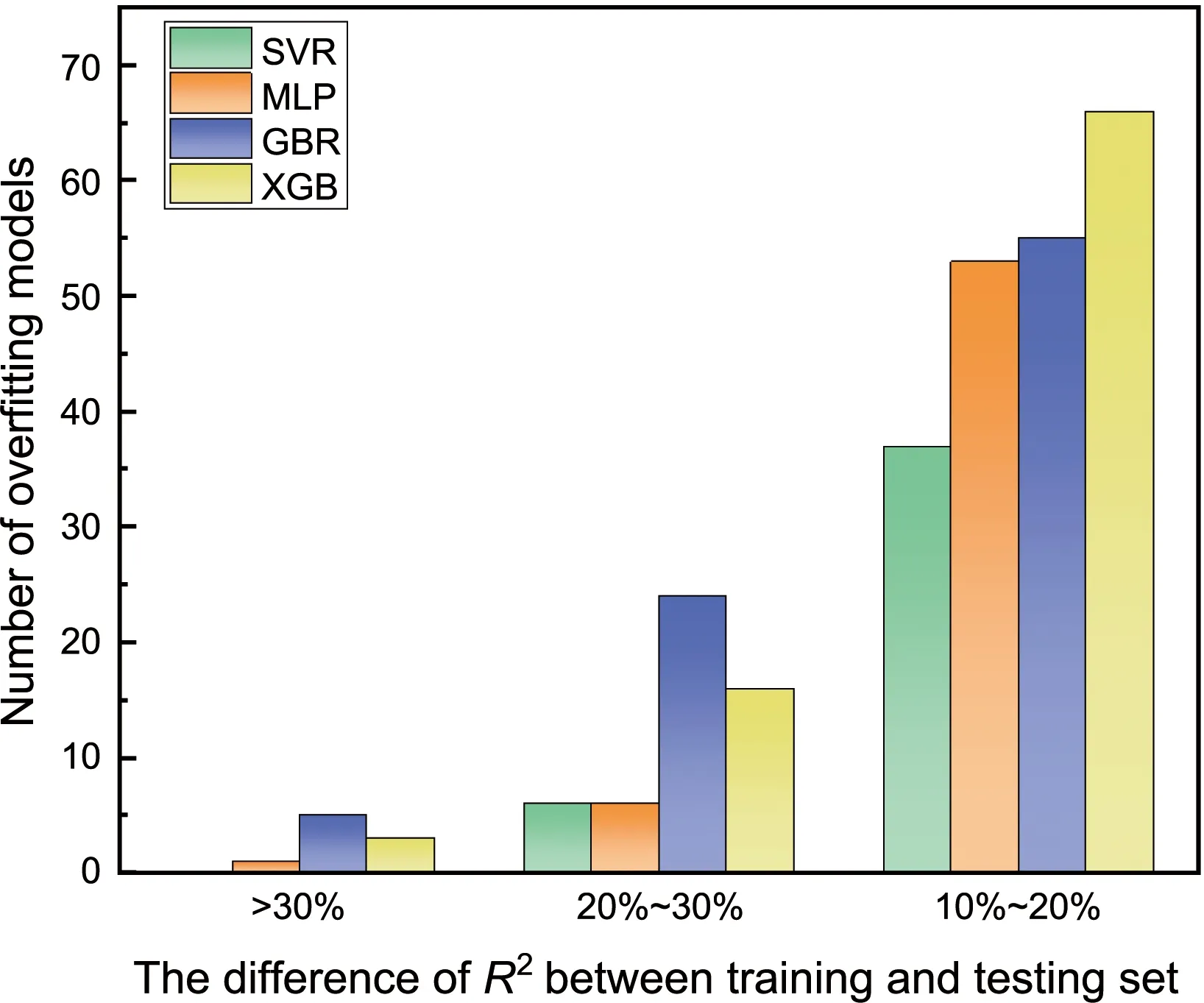
图6 过拟合程度分析Fig.6 The number of overfitting models

3.3 蠕变寿命的预测结果与合理性分析

由于对数据集进行了100次不同的随机划分，因此每个样本都能够多次被划分至训练集和测试集中，也就是说每个样本均可以获得多个预测。图7显示了SVR在不同数据集上的蠕变寿命平均预测结果。如图7a所示，SVR模型在训练集中表现为几乎所有的数据点都落在了斜率为1的直线上，误差棒也比较小，这一结果证明SVR模型在各自的训练集中都有着优异的性能。如图7b所示，在测试集中，SVR模型的表现不如在训练集中稳定，少量数据偏离了这条线，并显示出较大的误差条，这说明本研究中所使用的SVR模型对数据集的划分存在一定的敏感性。

图7 蠕变寿命预测结果：(a)SVR在训练集上的表现，(b)SVR在测试集上的表现，(c)SVR在少量新数据上的表现Fig.7 Creep life prediction results：(a)performance of the SVR model on the training set，(b)performance of the SVR model on the testing set，(c)performance of SVR model on a small amount of new data

为了进一步验证SVR模型的预测效果，基于文献调研，收集25个新数据，蠕变寿命范围为25.985～1364 h，与高温低应力这一蠕变机制基本吻合(其测试温度范围为900～1140 ℃，测试应力范围为124～392 MPa)[43-45]。图7c为SVR模型预测结果，其R2为84.44%，平均绝对误差值为0.3568。相比于测试集，SVR模型预测精度虽然出现一定程度的下降，但综合来看仍在可接受范围内，这也证明了基于物理冶金指导SVR模型具有良好的鲁棒性和可拓展性。

3.4 物理冶金参数的作用效果分析

为了进一步明确物理冶金参数在计算中所起到的作用，分别建立了不同层次的蠕变数据集(即原始特征+γ′相体积分数Vf、原始特征+晶格错配度δ、原始特征+扩散系数DL以及原始特征+两两组合的物理冶金参数)对SVR模型进行训练和测试。其中，数据集100次随机划分下，SVR模型在测试集上的平均绝对误差如图8所示。

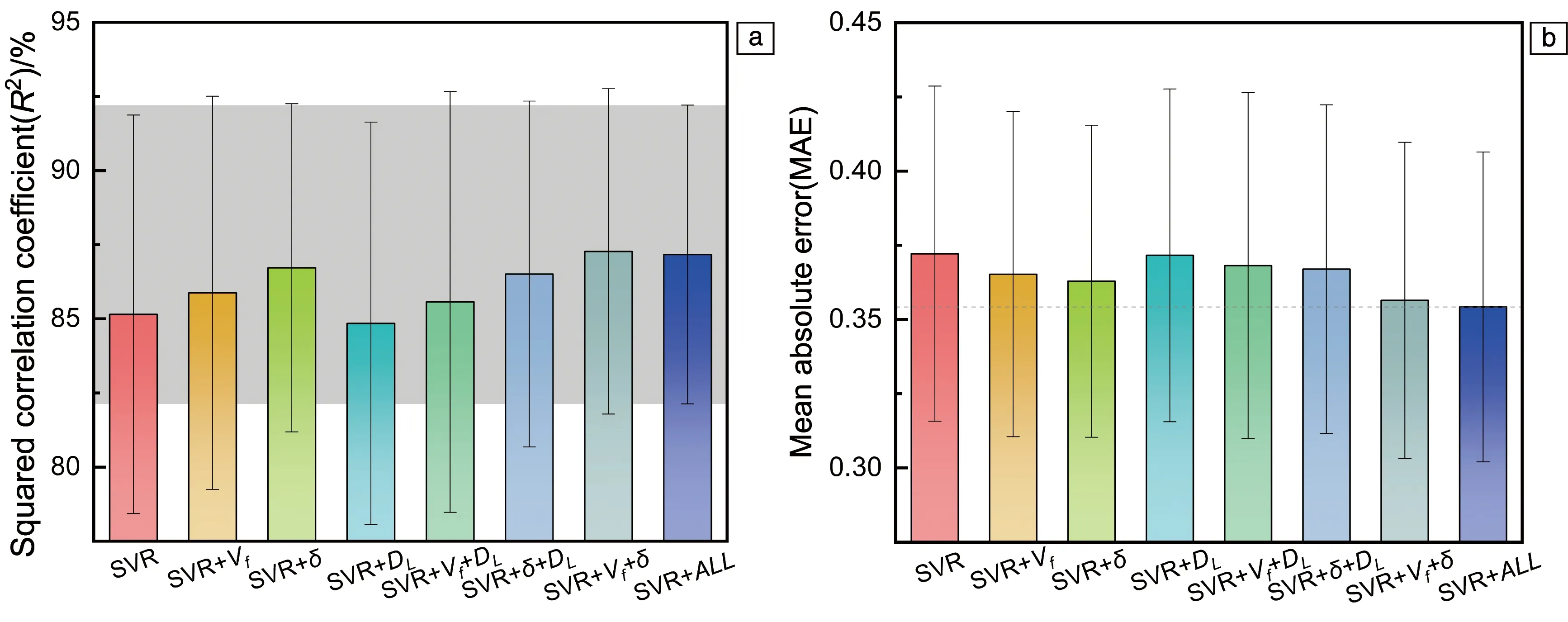
图8 基于不同程度数据挖掘的SVR模型在测试集上的表现：(a)R2，(b)平均绝对误差Fig.8 Performance of SVR model based on different levels of data mining on the testing set：(a)R2，(b)MAE

当模型的输入仅为成分工艺和测试条件时，SVR模型表现最差，而当使用原始特征和不同物理冶金参数作为输入时，模型的性能得到了一定提升。值得注意的是，在所有的模型中，模型SVR+Vf+δ与模型SVR+ALL的预测效果最好且相近，但是后者的平均绝对误差值更低同时R2和平均绝对误差的标准偏差更小，依此可以说明SVR+ALL拥有最好的预测效果。这进一步说明了在物理冶金原理的指导下对原始数据进行挖掘的重要性：物理冶金参数的引入不仅改善了机器学习模型的预测精度，同时可以改善模型的鲁棒性。

4 结 论

本文在充分调研国内外加速镍基单晶高温合金蠕变寿命预测的研究基础上，基于文献调研，建立起了高温低应力下的单晶高质量蠕变数据集，并且基于镍基单晶高温合金高温低应力下的蠕变机制，引入了三维物理冶金信息：γ′相体积分数Vf，晶格错配度δ，扩散系数DL。通过基于物理冶金指导机器学习的方法预测了高温低应力下镍基单晶高温合金的蠕变寿命，并且通过平方相关系数(R2)、平均绝对误差(MAE)、过拟合程度等方面对机器学习模型性能进行了评估，分析了物理冶金参数的作用效果。主要研究结论如下：

(1)基于Pearson系数的特征相关性分析表明，数据

集中的每个特征对蠕变寿命都有着自己的贡献；同时基于随机森林平均精确度降低的特征重要性评估表明，本研究中所使用的数据集在物理冶金学原理上存在一定合理性。

(2)基于7种经典的机器学习算法预测了合金的蠕变寿命，其中支持向量回归(SVR)模型的预测效果最佳，在训练集上的平方相关系数为96.88%，平均绝对误差值为0.1689；而在测试集上的平方相关系数为87.17%，平均绝对误差值为0.3542，并且拥有最少的过拟合模型个数。

(3)在引入三维物理冶金信息后，获得最高的平方相关系数和最小的平均绝对误差，同时降低了平方相关系数和平均绝对误差的标准偏差，说明物理冶金参数的引入改善了原始数据的质量，提高了SVR模型的预测准确性以及泛化能力。