表面装饰类石墨烯纳米粒子的磁性

秦伟凡, 吴 闯, 姜 伟

(1. 沈阳工业大学 理学院, 沈阳 110870; 2. 沈阳师范大学 实验教学中心, 沈阳 110034)

二维材料由于其独特的物理化学性质,受到了研究人员的广泛关注,例如石墨烯[1]、二硫化钼[2]、硅烯[3]等。其中,石墨烯是由英国曼彻斯特大学的2位科学家Andre Geim和Konstantin Novoselov[4]最早成功制备出的二维材料,二人由此获得了诺贝尔奖。石墨烯材料可以广泛地应用于纳米器件以及航空航天和生物医学等[5-6]领域。然而,完美无限大的石墨烯是不具有磁性的,通过剪裁、表面修饰[7]、掺杂[8]、缺陷[9]等方法可使其表现出独特的磁性,并使其在重金属离子的吸附与分离、传感器等领域有潜在的应用。Yuan等[10]报告了氮掺杂是提高石墨烯氧化物磁化强度和居里温度的有效途径,使其在自旋电子器件中的潜在应用成为可能。Kumazaki和Hirashima[9]研究了非磁性缺陷对石墨烯磁性能的影响,研究发现当一个子晶格上的缺陷数与另一个子晶格上的缺陷数不同时,缺陷周围可能会产生局域磁矩。基于第一性原理计算,Zhang等[11]预测石墨烯上装饰的5d过渡金属会呈现出一类独特的杂化体系,外加电场可以有效地控制其拓扑输运效应,从而使得这类材料的自发磁化方向被调控。Liu等[12]研究硅掺杂具有不同边缘的石墨烯纳米带的磁学性质,结果表明硅掺杂可以有效地调整系统的带隙和磁性。Si等[13]研究缺陷对石墨烯磁性的影响,发现缺陷的存在可以使石墨烯具有磁性。基于蒙特卡洛模拟方法,Sun等[14]对双层纳米石墨烯的磁性和热力性能进行了研究。在之前的研究中,学者们成功地应用蒙特卡洛模拟对石墨烯纳米带、硼烯等材料的磁性和热力学性能进行了详细研究[15-16]。然而,对表面装饰的类石墨烯纳米粒子的磁性研究相对较少,内在机理仍然需要进一步讨论。本文从微观量子的角度出发,采用蒙特卡洛的方法结合Ising模型研究了温度、表面亚铁磁交换耦合、内部铁磁交换耦合对表面装饰类石墨烯纳米粒子的磁性影响。

1 模型与方法

表面装饰类石墨烯纳米粒子简化模型如图1所示,其中箭头向上的球代表自旋为3/2的内部磁性离子,箭头向下的球代表自旋为2的表面装饰磁性离子;虚线和实线分别代表铁磁交换耦合作用J(>0)和J1(>0),点线表示亚铁磁交换作用J2(<0)。经过对模型结构分析,发现系统由4种独立子格子组成,它们的磁矩分别用M1-M4代表。

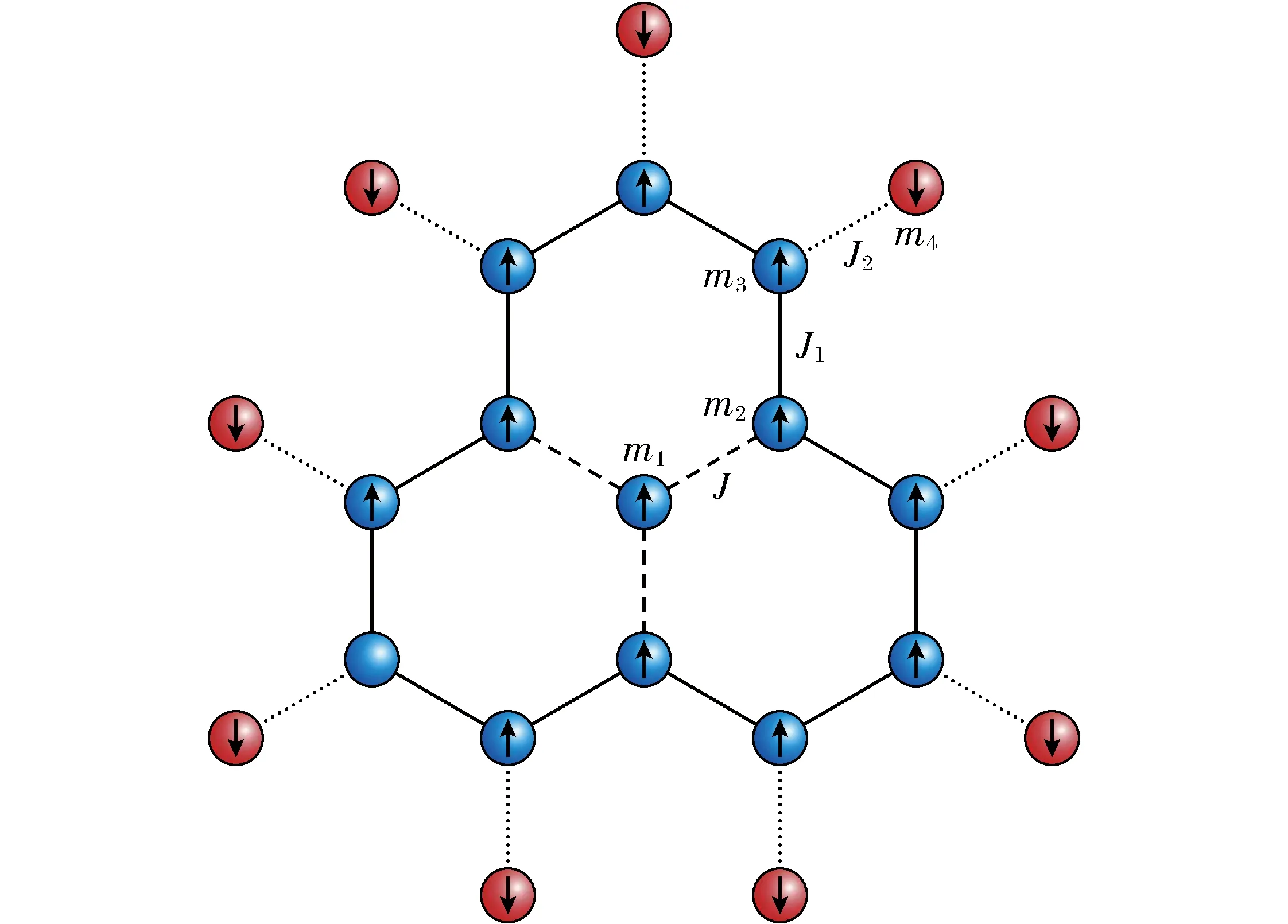
图1 表面装饰类石墨烯纳米材料模型Fig.1 Model of surface-decorated graphene-like nanoparticles

在考虑近邻交换作用和外场作用下,该模型的哈密顿量表示如下:

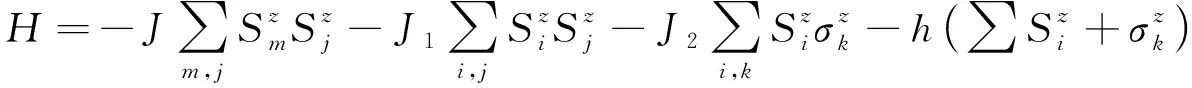
(1)

其中:S代表内部磁性离子的自旋值 3/2,可以取(±3/2,±1/2);σ为表面装饰磁性离子的自旋值2,可以取(±2,±1,0);h表示外磁场。哈密顿量前2项表示内部磁性离子之间的交换作用对哈密顿量的贡献,第3项表示内部和表面装饰磁性离子之间的交换作用对哈密顿量的贡献。

采用蒙特卡洛模拟方法对哈密顿量进行了求解,每个磁性离子翻转的依据是保持系统能量最低,从而得到系统的稳定结构。为了使计算结果可靠,确保系统处于稳定状态,本研究舍弃了前面的40万步,计算其余的10万Monte Carlo(MC)步。具体流程如图2所示。

图2 计算流程图Fig.2 Calculation flow chart

为了研究表面装饰类石墨烯纳米粒子的磁性,引入统计物理中正则系统求热力学量平均值的公式:

(2)

其中:Z为配分函数;kB是玻尔兹曼常数;H(x)是系统的哈密顿量;T是热力学温度;N是系统总的原子个数。由上述公式可以求出磁矩M的表达式为

(3)

系统总的平均磁矩为

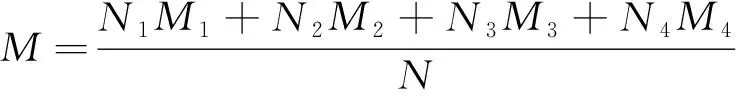
(4)

其中:磁性离子的数量分别为N1=1,N2=3,N3=9,N4=9;N为总磁性离子数。

系统磁化率χ计算公式如下:

(5)

2 计算结果分析与讨论

本节主要研究交换耦合J1,J2对表面装饰类石墨烯纳米材料磁矩、磁化率、阻碍温度和阶梯效应的影响。在计算过程中,将铁磁交换耦合J作为单位,即J=1。选择内部磁性离子的自旋方向与磁场方向相同,表面装饰磁性离子的自旋方向与磁场方向相反。数值计算结果如图3～图6所示。

(a) 磁矩(M)随J1变化曲线(b) J1=0.8时,子格子磁矩曲线(c) 磁化率(χ)随J1变化曲线(d) 阻碍温度随(J1)变化曲线

铁磁交换耦合作用J1对系统磁性影响如图3和图4所示。图3(a)为J2=-1.4,h=1时铁磁交换耦合J1对磁矩的影响,由图中可以看出磁矩曲线从饱和磁矩MS先升高到一个峰值再逐渐降低,最后趋于一个恒定值。随着J1的增加,磁矩曲线的峰值也逐渐增大。磁矩曲线的形状是由交换耦合作用引起的有序能和分子热运动引起的无序能之间竞争的结果,说明磁交换耦合J1对系统磁矩有较大影响。在选定参数范围内,总饱和磁矩为MS=3/44。由公式(4)可知,总饱和磁矩值取决于各个子格子的饱和磁矩。因此,计算了J1=0.8时4种子格子随温度的变化,计算结果如图3(b)所示,其中M1=M2=M3=3/2,M4=-2.0。总饱和磁矩计算如下:

(a) 总磁矩阶梯效应(b) 子格子磁矩阶梯效应

Ms=(M1+3M2+9M3+9M4)/22=(3/2+3×3/2+9×3/2+9×(-2))/22=3/44

与图3(a)中的总饱和磁矩一致。磁化率是衡量系统磁学性质的重要参数,根据公式(5)计算出磁化率随温度的变化规律,计算结果如图3(c)所示,所选择的参数与图3(a)一致。磁化率曲线峰值对应的温度称为阻碍温度,随着J1的增加,阻碍温度逐渐向高温区移动,例如J1=0.8, 1.3, 1.8, 2.3时,对应的阻碍温度分别为TB=1.35, 1.40, 1.55, 1.65,说明系统有序能占主导地位的温区随着J1的增大而增大。图3(d)给出了不同外场下阻碍温度随J1的变化,在相同的交换耦合作用下,阻碍温度随着外场的增加而变大;在相同的外场下,阻碍温度随着J1的增大而增大,与图3(c)的趋势一致。

在低温下,系统磁矩随着外磁场的变化发生跳跃,出现磁化台阶的现象称为阶梯效应。磁化台阶的数量主要取决于各个磁性离子的自旋值和所选择的交换耦合值。图4 给出了当J1=0.5和1.5时磁矩曲线出现的阶梯效应。由图4(a)可以看出,随着外场(h)的增加,出现2个磁化平台,分别为M=-3/44和M=75/44。这主要是因为随着外磁场的增加,磁性离子得到的外加磁场能逐渐增加,使其自旋发生翻转。系统磁矩达到饱和状态所对应的磁场被称为饱和磁场,图中虚线所指的横坐标为饱和磁场(hs)。随着J1的增加,饱和磁场逐渐增加,例如J1=0.5和1.5时,对应的饱和磁场分别为hs=3.0和4.5。为了解释2个磁化平台出现的原因,给出了各个子格子磁矩的阶梯效应,结果如图4(b)所示。从图4(b)中可以发现,M1(M2,M3)子格子随着外场的增加出现2个磁化平台,分别是-3/2和3/2,而子格子M4则保持磁矩2.0不变,说明系统的总磁矩的翻转是由子格子M1(M2,M3) 贡献的。

亚铁磁交换耦合J2对系统磁性的影响如图5和图6所示。图5(a)给出了J1=0.8,h=1,J2=-0.7, -1.1, -1.4和-1.7时的磁矩曲线。随着J2的变化,饱和磁矩与图3(a)一致,仍然为MS=3/44,随着|J2|的增加,磁矩曲线的峰值逐渐降低,说明表面修饰亚铁磁交换耦合J2对系统磁矩有较大影响。图5(b)给出了J2=-1.1时各个子格子的磁矩,其中M1=M2=M3=3/2,M4=-2.0。结果与图3(b)一致。由此说明,2种交换作用对饱和磁矩的影响效果是类似的。图5(c)给出了亚铁磁交换作用J2对磁化率随温度变化的影响,磁化率峰值对应的阻碍温度随着|J2|的增加而增大,例如|J2|=0.7, 1.1, 1.4, 1.7时,对应的阻碍温度分别为TB=1.25, 1.30, 1.35, 1.45。为了研究外场对阻碍温度的影响,图5(d)给出了不同外场下阻碍温度随J2的变化。在相同的交换作用下,阻碍温度随着外场的增加而变大,在相同的外场下,阻碍温度随着|J2|的增大而增大,与图5(c)的趋势一致。

(a) 磁矩(M)随J2变化曲线(b) J2=-1.1时,子格子磁矩曲线(c) 磁化率(χ)随J2变化曲线(d) 阻碍温度随J2变化曲线

(a) J2=-0.4阶梯效应(b) J2=-4.8阶梯效应

为了研究亚铁磁交换耦合对阶梯效应的影响,图6(a)～图6(b)给出了低温下系统总平均磁矩和各个子格子磁矩随外磁场的变化曲线。当J2=-0.4时,随着外场(h)的增加,出现2个磁化平台,分别为M=-3/44和M=75/44。这2个磁化平台的来源与图4中铁磁交换作用对阶梯效应的影响类似。虚线对应的磁场为饱和磁场,hs=4.5。图6(a)右侧为对应的子格子阶梯效应曲线,子格子M1(M2,M3)仍然保持自旋由-3/2翻转为3/2的2个磁化平台,M4子格子则保持磁矩2.0不变。饱和磁场为子格子M1(M2,M3)发生翻转对应的磁场。当改变J2=-4.8时,随着外场(h)的增加,出现3个磁化平台,分别为M=-3/44,M=21/44和M=75/44。这主要是由于随着外磁场的增加,M1(M2)磁矩先由-3/2翻转为3/2,产生第2个磁化平台,随着外场的继续增加,子格子M3磁矩又由-3/2翻转为3/2,产生了第3个磁化平台。第2个磁化平台临界磁场hc=4.5,第3个磁化平台所对应饱和磁场hs=9.6。说明磁场和亚铁磁交换耦合共同作用影响子格子自旋态的翻转,出现多个磁化平台。

3 结 论

在本文中,用混自旋3/2和2的Ising模型描述表面装饰的类石墨烯纳米粒子,基于蒙特卡洛模拟,利用数值计算方法研究了该系统的磁性。内部铁磁交换耦合和表面装饰的亚铁磁交换耦合对系统的磁矩和磁化率有重要影响,在一定磁场的作用下,这2种交换耦合增强会增大系统的阻碍温度;交换耦合和磁场共同作用会影响系统的子格子的自旋翻转,从而影响总的平均磁矩,出现多重磁化平台,产生阶梯效应。