基于CNN-DE-SVM的滚动轴承故障诊断研究

梁川, 陈雪军

(华润江中制药集团有限责任公司,江西,南昌 330096)

0 引言

随着科学技术的不断进步,人类社会的生产力水平也发展到了一个新的阶段。现代工业体系相比传统工业体系有着更高的生产效率,但高度的集成化也导致现代工业体系中每一件机械甚至每一个部件都与整体的生产息息相关。因此,为了保证工业系统的正常运作,故障诊断技术已然成为现代工业体系中的关键组成部分[1]。

滚动轴承作为工业系统中使用最为广泛的机械部件之一,一旦在运行过程中出现故障,轻则影响自身所在的机械设备,重则传导至整个生产线。因此,对滚动轴承开展故障诊断研究有重要的工程意义。

张柯等[2]提出了一种基于多模态注意力机制的卷积神经网络,并利用小波变换对原始数据进行处理,结果表明此模型可以有效地识别变工况下的各类轴承故障,在实际应用中也取得了较好的结果。LIU等[3]提出了一种改进的傅里叶变化,并利用此方法结合多尺度排列熵提取故障特征,最后利用BP神经网络实现故障状态的识别。

滚动轴承故障大致归类为内圈、外圈、滚动体和保持架四大类典型故障。因此,本文基于滚动轴承的典型故障开展研究,以公开滚动轴承数据集为对象,使用本文所提出的故障诊断模型进行验证,从而表明此模型具有推广企业滚动轴承自测数据集的潜力。

文献[2-3]给出的研究都是以人工智能算法为基础的故障诊断研究,这是目前的主流方法,但上述故障诊断模型在特征提取能力或诊断精度上都存在一定的短板。首先,特征提取是故障诊断中的关键步骤,决定了诊断精度的上限。现有诊断模型大多都是利用信号分析方法进行特征提取,如短时傅里叶变化、功率谱、小波包变换等[4]。但这些信号分析方法都有一定的局限性,如短时傅里叶变换不适用于频率变化较大的信号、小波包变换需要预先选择基函数等问题,从而影响整个诊断模型的适用性。其次,人工智能算法如支持向量机、随机森林和聚类算法等,都包含需要调节的参数。这些超参数的设置如果不恰当,将会极大地降低模型的性能。如果利用人工手动调节这些参数,需要花费更多的人力成本,同时也降低了模型的鲁棒性。

针对上述问题,本文提出一种基于CNN-DE-SVM的故障诊断模型。首先,利用CNN强大的特征提取能力,从原始的轴承数据中提取出抽象特征,再将此特征输入DE-SVM故障诊断模型中。其次,利用差分进化算法自适应调节SVM中关键的2个参数惩罚因子C和核函数参数γ,从而使得SVM拥有更高的诊断精度。最后,设置一组对比实验,验证CNN的特征提取能力与DE算法的优化效果,从而表明所提出的CNN-DE-SVM模型拥有更高的工程应用价值,摆脱了现有模型需要人工参与的缺点,在节约人力成本的同时提高了模型的诊断精度。

1 卷积神经网络

卷积神经网络是目前使用最为广泛的神经网络模型之一,在姿态识别和图像分析等领域都有应用[5-6]。CNN的优异性能主要得益于其强大的特征提取能力,原始数据输入CNN后,会经过反复的卷积和池化操作,将原本可解释的原始数据转换为不可解释的抽象特征。虽然人工无法识别抽象特征所具有的意义,但CNN的全连接层可以从中获取特征与标签所存在的关系,进而建立分类模型实现对应的功能。但全连接层的分类能力较弱,因此本文将卷积层和池化层所提取出的抽象特征输入SVM中,从而实现故障诊断的功能。

卷积神经网络的核心就是卷积层,由多个卷积核组成,通过卷积运算,卷积核会得到新的特征图,然后进行非线性计算[7]。在进行卷积操作之前,CNN首先会将数据的结构进行重组。本文使用二维CNN模型进行特征提取,因此需要将原始数据重构为数据矩阵的形式,再利用卷积核扫过这个数据矩阵,进行乘法运算后得到特征图并通过激活函数激活输出至下一层[8],数学公式如下:

(1)

式(1)中,⊗为卷积运算,xi为输入卷积核的特征向量,ki为卷积核的权值,bi为卷积核对应的偏置,Mi为卷积层的输出,i为对应的层数。计算出来的特征图还需要经过非线性激活,本文选用Sigmoid函数进行激活。

通过卷积层得到的特征图再输入池化层中,用于降低数据维度,同时也能减少过拟合的风险。池化层的具体降维方法有许多,本文使用最大值池化法,即从所框定的范围内选择数值最大的特征,数学表达式如下:

R=maxMi

(2)

式(2)中,max为池化运算,R为池化层的输出。

2 DE-SVM模型

2.1 SVM基本原理

支持向量机是在统计学的基础上所形成的一种人工智能算法,本质上是一种二分类方法,利用超平面使两类样本分开。它的主要优势表现在收敛速度和性能上,在小样本、高维度的情况下仍具有较强的泛化能力。

为了使得此超平面有最好的鲁棒性,SVM需要样本中距离超平面最近的向量与超平面的距离最远。如此一来便可以最大程度上保证超平面设置的合理性。惩罚因子C和核函数参数γ对SVM最终的分类结果有着直接的影响。因此,合理且高效地确定出它们的取值对于提高SVM的工程应用价值有着关键的作用。

2.2 DE-SVM模型的构建

差分进化算法是一种进化算法,最早是由STORN等[9]于20世纪90年代所提出的。与其他类似的算法相比,DE算法最显著的特点是控制参数较少,仅有两个。因此,算法的可操控性强,且寻优能力优异。本文利用DE算法寻优SVM参数的取值,其具体的模型构造流程如下。

(1) 初始化种群

DE算法的第一步为构造初始化种群,即在搜索空间中随机生成一系列的初始个体向量,可表示为

(3)

式(3)中,qi代表初始种群中的第i个个体向量,个体向量的维度为2,由SVM中的超参数C和γ所组成。Uc和Vc为惩罚因子取值范围的上限和下限,Uγ和Vγ为核函数参数取值范围的上限和下限。文献[10]指出取值范围在(0,100)的区间内为宜,因此本文设置Uc=Uγ=100,Vc=Vγ=0.01。rand(0,1)为随机生成的0至1上的实数。本文设置初始种群中个体向量的个数为30,即依据式(4)随机生成30个个体向量。

(2) 变异

变异操作是DE算法中的核心步骤,可以让个体向量在保证一定的多样性的同时,向着一个或多个近似最优点收敛。本文所使用的变异算子如下:

vi,g=q1,g+K(qbest,g-q1,g)+F(q2,g-q3,g)

(4)

式(4)中,q1,g、q2,g和q3,g为第g代种群中互不相同的3个个体向量,qbest,g为第g代种群中适应度值最好的个体向量,在本文中为使得SVM诊断精度最高的个体向量,vi,g为变异向量,K为随机生成的0至1上的随机数,F为缩放因子,作用是控制种群的进化速度,其数值一般不超过1,本文参考文献[10]设置F=0.8。

(3) 交叉

交叉操作是DE算法的第三步,其作用是增加种群的多样性。本文所选用交叉策略的数学表示式为

(5)

式(5)中,oi,k,g代表实验向量,i、k和g分别代表向量的个数、向量的维度和进化代数,个体向量q和变异向量v同理,CR代表交叉概率,本文依据文献[10]设置CR=0.6。

(4) 选择

DE算法的选择策略在本质上属于一种贪婪学习,即从实验向量和个体向量中选择最优的一个进入到下一代,其数学表达式为

(6)

式(6)中,g( )代表适应度函数值。在本文中适应度函数为1减去向量中的C和γ代入SVM模型中所取得的诊断精度。

3 故障诊断实验

3.1 数据来源

所选用的滚动轴承数据来自公开大学滚动轴承数据中心[11],以此数据集为基础验证所提故障诊断模型的有效性,进而在一定程度上表明此模型推广应用至某企业生产基地滚动轴承自测数据集时的可行性。某企业生产基地中监测的机械设备有电机和齿轮箱等,基本都包含滚动轴承。滚动轴承在实际使用过程中所发生的典型故障有内圈剥落、外圈剥落、滚动体磨损等,因此本文同样选用公开大学滚动轴承数据集中的内圈故障、外圈故障、滚动体故障等数据开展故障诊断研究。具体所选用的数据如表1所示。

表1 数据介绍

本文使用的编程框架为TensorFlow2.0,计算机硬件配置为8 GB的运行内存,CPU型号为i5-4300U。

3.2 CNN特征提取

利用二维CNN提取滚动轴承振动数据的特征。以I1内圈故障的样本为例,该样本中一共包含121 535个连续采样的样本,选用其中前51 200个样本,将其重构为16×16的数据矩阵,一共可以得到200个16×16的数据矩阵。再将这200个数据矩阵输入CNN中进行特征提取,示意图如图1所示。

图1 CNN特征提取流程

观察图1,以任意1个数据矩阵为例,其结构为16×16×1,首先经过16个3×3的卷积核,从而得到16×16×16的卷积特征图;再经过2×2的最大值池化层,数据结构变为8×8×16;再经过32个3×3的卷积核,数据结构变为8×8×32;再经过2×2的最大值池化层,数据结构变为4×4×32;最后只经过一层全连接层,数据结构变为1×1×256,即为CNN所提取出的特征。

重复上述步骤,将每一类轴承数据都输入CNN,最后一共可以得到2000组样本,每一个样本所包含特征个数为256,即2000×256的输入矩阵。对于SVM等机器学习模型,256个特征过多,容易导致算法模型出现过拟合的情况。因此,使用主成分分析法(PCA)[12]对其进行降维。依据PCA的基本原理并计算出数据矩阵主要的特征值,最后将其降至三维。

为了直观地体现CNN结合PCA特征提取的能力,同时考虑到过多的特征在单一视角下容易出现重叠,仅选择4类数据并将其可视化,如图2所示。

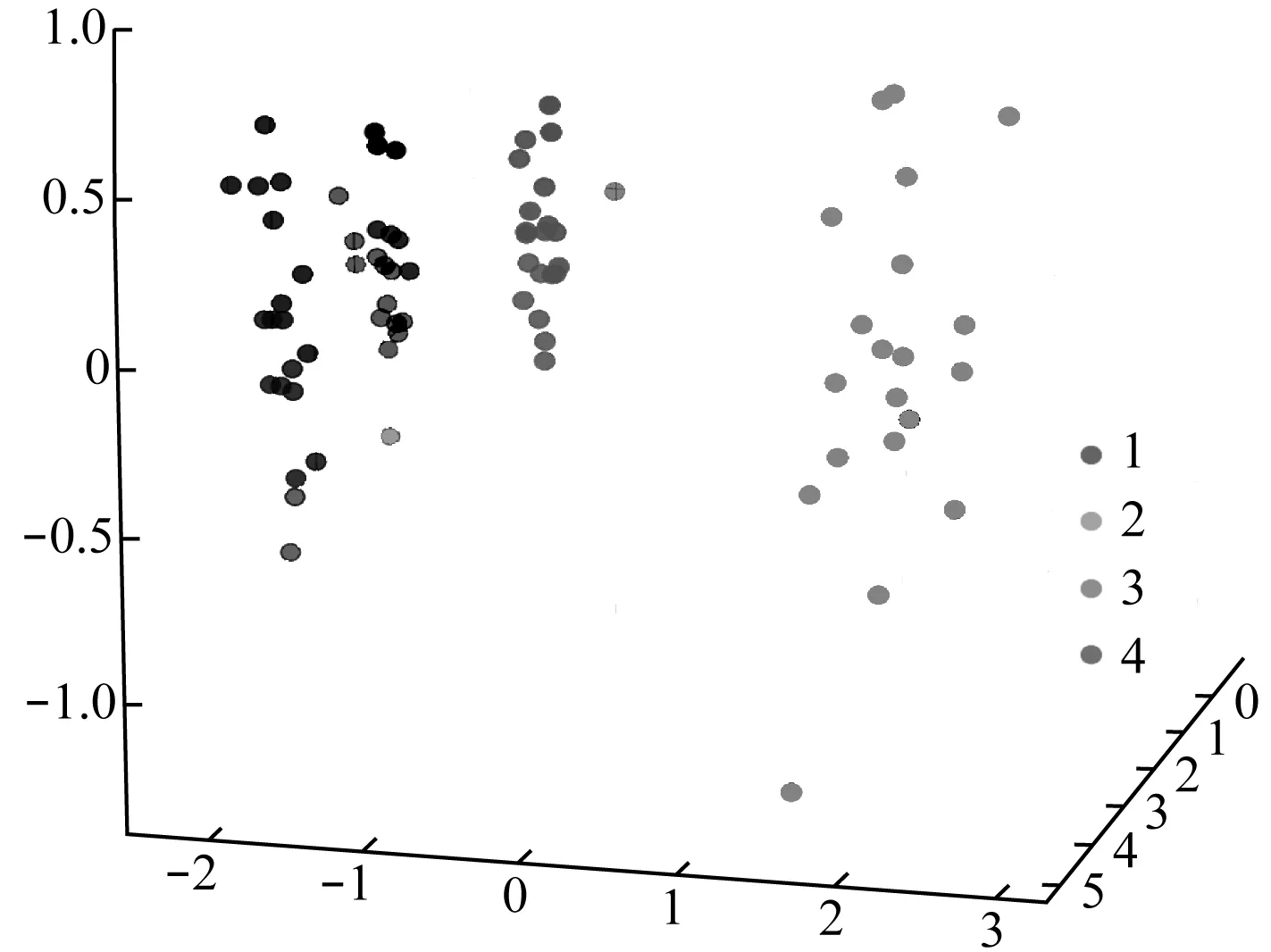
图2 特征提取效果

观察图2可知,4类不同的数据相互分隔,表明特征工程有效地将振动数据与标签的抽象关系提取出来了,有助于提高算法模型的精度上限。

原始数据经过CNN结合PCA的特征提取之后,随机划分其中的70%作为训练数据,30%作为测试数据,再输入DE-SVM模型中实现故障诊断的功能。

3.3 故障诊断实验

设置DE算法的迭代次数为50,设置初始种群中所包含的个体向量的个数为30。DE-SVM优化曲线如图3所示。

图3 DE-SVM优化曲线

从图3可以观察到,SVM经过优化之后,最后的精度可以达到99.80%。

为了进一步表明本文所提故障诊断模型的有效性,设置一组算法对比实验。

在特征提取方面,使用小波包分解(WPD)与CNN进行对比。在诊断模型方面,使用未经优化的SVM进行对比。对比结果如表2所示。

表2 诊断结果对比

分析表2可知:由于WPD在特征提取能力上存在一定的不足,从而导致故障诊断模型的精度上限较低,利用DE-SVM模型只能取得91.32%的诊断精度,使用标准SVM则只能取得85.78%的精度;利用CNN进行特征提取,即便是标准SVM模型也能取得96.57%的诊断精度;而利用DE-SVM进行故障诊断则能取得上述4类算法的最高精度99.80%。这进一步表明了CNN特征提取的有效性和DE算法的优化性能。同时,上述分析也表明CNN-DE-SVM模型具有推广至华润江中药谷生产基地滚动轴承自测数据集的应用潜力。

4 总结

本文以公开轴承数据集为研究对象,使用CNN结合PCA的特征提取方法从振动数据中提取出更加有效的抽象特征,再将此特征输入DE-SVM的故障诊断模型当中,进而实现滚动轴承振动数据从特征提取直至故障诊断的全过程智能化,无须进行繁琐的信号分析以及人工参数调优。最后,通过算法对比表明本文所提出的CNN-DE-SVM故障诊断模型还拥有更高的诊断精度。