基于代价敏感思想和自适应增强集成的SVM多分类算法

何旭, 席佩瑶, 辛云宏

(陕西师范大学物理学与信息技术学院,陕西,西安 710072)

0 引言

在科学研究和实际应用中,人工智能[1-2]越来越受到研究者的青睐,而数据挖掘是人工智能重要组成部分,数据分类作为数据挖掘的基本手段和重要方法,也被深入研究和优化。文献[3]为提高下肢表面肌电信号步态识别的准确性,提出了一种基于粒子群(PSO)算法优化SVM的模式识别方法;文献[4]将最小闭合球算法引入AdaBoost-SVM算法框架中构成CSVM算法;文献[5]提出了基于贝叶斯分类器和Boosting算法的SVM组合模型,有效提高了软测量模型的泛化能力;文献[6]提出了自适应增强的SVM集成算法(SVME)在一定程度上提高了对风机故障类型诊断的识别正确率。本文通过采用SVM对数据样本进行识别分类,提出一种基于代价敏感思想和自适应增强的SVM集成数据分类算法(CAB-SVM)。通过实验结果表明,CAB-SVM集成算法与个体SVM和SVME集成算法相比正确识别率提高了。

1 CAB-SVM算法

CAB-SVM算法的基本框架如图1所示,首先输入样本数据集,利用AdaBoost算法迭代训练SVM弱分类器,同时计算弱分类器的分类误差和在弱分类器中所占权重。在权重更新阶段,要增加被分错样本权值,为了加快这部分样本权值增加,引入代价敏感思想,即当被分错的样本权值快速增加,被正确分类的样本权值加快减小。更新结束后得到新的样本集的权重分布,再抽取样本组成临时训练集训练下一个新的SVM弱分类器。继续进行迭代训练,直至结束。最后将训练出的所有SVM弱分类器根据权重线性相加,得到强分类器集成模型。

图1 CAB-SVM算法体系结构

1.1 支持向量机

支持向量机是在结构风险最小化[7]原则的基础上提出的一种机器学习方法,它是定义在特征空间上间隔最大的分类器。对于实现二分类问题,假设训练集G中存在d维t个样本,G=(xt,yt),其中xi∈Rd,yi∈{+1,1},i=1,…,t。超平面(wo·x)+b=0把这些样本分类,设定决策函数为

f(x)=sign(wox+b)

(1)

接下来引入松弛变量δi和松弛因子c以构造约束最优化问题,构造Lagrange函数,再对β、b、δi求偏导,分别使其等于0,根据KKT条件,可得到ω和b的最优解ω*和b*:

(2)

(3)

再将最优解ω*和b*代入式(1),对于引入核函数K(xi,yj)的核支持向量机的情况,判别函数为

(4)

1.2 构建CAB-SVM模型算法

AdaBoost[8]算法在1995年由Freund等提出,是典型的Boosting算法,AdaBoost-SVM算法近年来被许多有关学者广泛关注[9]。本文提出基于SVM分类器上引入自适应增强算法和代价敏感思想[10-11]的分类算法CAB-SVM,详细流程图见算法1。

算法1: CAB-SVM算法步骤输入:训练样本集X=(xt,yt)输出:H(x)1:式(5)计算初始化样本权值分布D12:计算每类样本的数目nk.3:式(9)计算样本的错分代价Ci4:for q=1,…,Q a.式(7)计算抽中概率 b.优化参数σ和c c.训练弱分类器 d.式(8)计算分类误差eq e.式(9)计算分类器所占权重αq f.式(10)(11)更新训练集的权值分布endReturn 1,…,q,…,hQ5:式(11)输出强分类器H(x)

首先进行样本权重初始化,每个样本赋予相同的权重,D1是表示初始样本权重分布,wi表示训练样本权重,如式(5):

(5)

从样本集t个样本中抽取h个样本作为临时训练样本集,样本抽中概率为

(6)

样本集权值调整更新阶段,将代价调整函数ζ引入公式中。ζ函数的公式如下:

ζ+,i=-0.7(yifq(xq))ci+0.7

ζ-,i=0.7(yifq(xq))ci+0.7

(7)

其中:

(8)

式(8)～式(9)中,t表示样本集总数,nk表示第k类样本共nk个样本,ζ+表示模型预测正确时函数,ζ-表示为模型预测错误时的函数。

当hq(Xq(i))≠yi,下一轮权重分布如式(9):

(9)

当fq(Xq(i))=yi,下一轮权重分布如式(10):

(10)

最后将训练出的SVM弱分类器据权重线性相加得到强分类器,如式(11):

(11)

综上,CAB-SVM模型算法通过AdaBoost用于SVM弱学习器的训练中,继而引入代价调整函数,以至在下次迭代时弱分类器着重学上轮错分样本。

2 实验及结果

2.1 实验数据集

为了检验本文提出CAB-SVM算法的识别性能,实验数据组data-20、data-21是信号检测实验室现场采集,另外使用UCI标准数据库中的数据集,它们分别是vowel、ecoli、glass。实验数据集信息如表1所示。

表1 实验数据集信息表

2.2 实验设计与结果分析

本文实验将CAB-SVM算法与SVME集成算法、SVM算法结果进行比较,分析这3种算法的正确识别率。在分类实验中,训练样本集数目和测试样本集数目比值为4∶1,分类结果如表2所示。

表2 基于不同方法的SVM分类器分类效果比较

将每套数据分别代入3种算法中测试,每套数据在每个算法中分别进行10次实验,最终取10次实验结果的平均值为最终的实验结果。由图2可以看出,本文提出的CAB-SVM集成算法具有更高的正确识别率,是因为其区别于个体SVM的以下优势:①迭代训练个体SVM的样本集不同;②迭代训练个体SVM的RBF核函数的参数σ和惩罚因子c不同;③迭代训练个体SVM中,样本权重更新公式引入了代价敏感思想;④迭代训练个体SVM的分类识别性能逐渐强大。

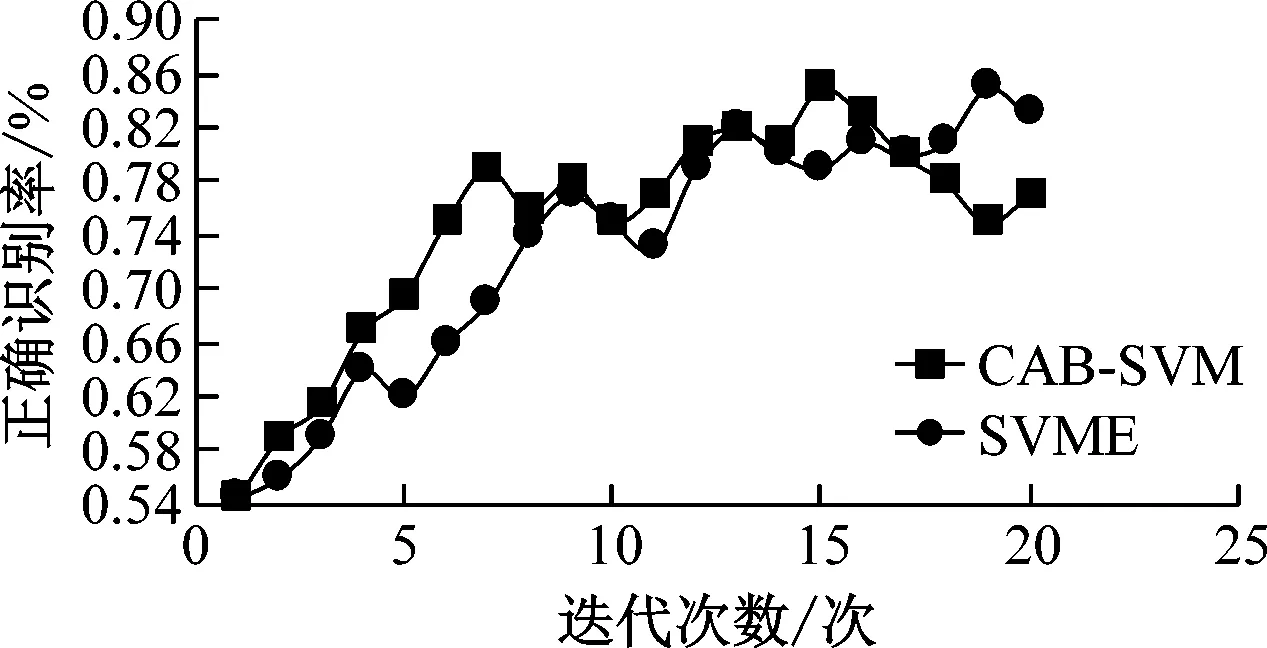
(a) data-21的实验结果

图2为利用CAB-SVM和SVME两种集成方法对这10组数据集分别进行训练的实验结果。横坐标表示用集成算法的分类器个数,纵坐标表示相应的集成方法的正确识别率。

由图2可知,当集成算法的分类器个数较少时,分类器集成的正确识别率较低。实验结果证明,CAB-SVM和SVME两种集成算法在达到相同较高的正确识别率时,CAB-SVM所用的分类器集成个数总体上少于SVME所用的分类器集成个数。综上所述,CAB-SVM算法相比SVME算法有效地减少了迭代次数,更适宜应用到有关数据识别分类的工作当中。

3 总结

本文在传统SVM分类器研究基础上,提出了一种自适应增强CAB-SVM算法即在集成算法的每次迭代学习中通过快速更新样本的权重,个体分类器主要学习训练易错分的样本,这样使得分类器的识别性能和效率都得到了有效的提升。本文实验中所提出的自适应增强CAB-SVM算法虽然提高了正确识别率,但是在运算过程中所需运行时间较长,对于这一点还需进一步研究和改进。