渗透转化思想 助力学生深度学习“图形与几何”
2023-10-12黎美薇
文/黎美薇
常用的数学思想有很多,转化思想是最基本、最常用的一种思想,在小学数学教学中有着广泛的应用价值。小学数学“图形与几何”中蕴含转化思想的内容较为丰富,如“多边形的面积”“立体图形的面积”“立体图形的体积”[1]。在“图形与几何”教学中渗透转化思想,可以使学生获得解决数学问题的有效途径。
一、深入研读教材,挖掘转化思想
数学教材是数学知识的载体,教师要深入研读教材中的“图形与几何”内容,分析知识领域间的知识结构、作用,探寻具体知识背后的合适方法,挖掘转化思想,夯实课堂教学基础。
例如,圆的面积以长方形的面积为基础。在学习圆的面积时,学生需要转化已有的知识经验,将未知面积公式的平面图形转化为已知面积公式的平面图形。简单地说,学生要平均分圆,拼成一个近似于长方形的图形。接着,学生要对比圆和这个近似于长方形的图形,发现二者之间的联系,然后迁移已有认知,回想长方形的面积公式,列出算式并化简,得出圆的面积公式。通过探寻知识背后的合适方法,教师挖掘出了转化思想,引导学生体验数学操作活动,经历转化过程,借此实现知识间的融会贯通,扎实掌握转化思想与方法,发展几何直观素养,实现深度学习。
二、精选教学方法,融入转化思想
“图形与几何”中的大部分内容具有抽象性,对于大部分小学生而言存在较大的理解难度。应用转化思想,可以在一定程度上降低“图形与几何”内容的抽象性,助力学生直观化、形象化、具体化地探究数学内容,建立深刻的认知[2]。
例如,“圆的面积”这节课的教学重点是让学生将圆平均分为32 份或64 份,拼接、转化为一个近似于长方形的图形。将圆平均分为32 份或64 份,对于大部分学生而言有一定困难。针对此情况,在教学“圆的面积”之前,教师以转化圆为近似于长方形的过程为重点,录制微课,动态展现转化过程。在课堂上,教师先引导学生回顾平行四边形、三角形的面积推导过程,总结方法。大部分学生迁移已有认知,在脑海中浮现不同的推导过程,发现相似之处,总结出具体方法——经过剪切、拼接,将未知面积公式的图形转化为已知面积公式的图形。之后,教师鼓励学生发挥想象力,设想“可以将圆剪切、拼接为什么图形?”学生发散思维,积极联想,提出不同的猜想及操作方法。大部分学生提道:“可以将圆平均分成不同的份数,剪切、拼接,得出一个新图形。”教师对学生进行赞赏,并借助电子白板播放微课。在观看微课时,学生发现“随着平均分的份数越多,拼出的图形越来越像长方形”(如图1)。
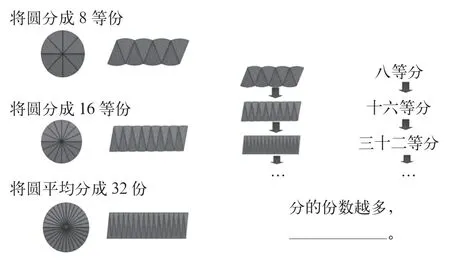
图1
于是,教师鼓励学生对比圆和近似长方形的图形,分析、总结二者之间的关系。在此过程中,大部分学生迁移已有认知,对比圆的周长、半径与近似长方形图形的长、宽,直观地发现二者之间的关系。无须教师引导,学生主动回想、书写长方形的面积公式,并应用发现的关系,延展公式、简化公式,得到圆的面积公式。教师依据学生的学习情况,总结具体方法和数学思想。之后,教师鼓励学生设想其他方法,将圆转化为其他熟悉的图形,继续探究圆的面积公式。
三、积极实践操作,应用转化思想
(一)在知识生成中应用转化思想
学生探究知识的方式有很多,实践操作是其中之一。实际上,实践操作的过程正是学生亲历转化的过程。在此过程中,学生会积极思考,迁移已有认知,透过数学现象发现结论,扎实掌握数学知识,获取转化思想,发展形象思维能力、归纳总结能力。
例如,在教学“圆的周长”时,教师先引导学生探究圆的周长的内涵。在探究后,大部分学生认识到“围成圆的曲线的长是圆的周长”。基于此,教师鼓励学生探究圆周长计算方法。在探究时,学生主动与其他小组成员交流。部分小组成员迁移已有认知,联想有关方法并主动分享。如有的组员提出:“可以用绳子绕着圆套一圈,绳子的长度就是圆的周长。”在此提议下,小组成员动手操作,并测量绳子的长度,记录数据。之后,小组成员观察、比较绳子的长度和圆的直径,发现绳子长度是圆的直径的3 倍多一点。面对如此发现,小组成员继续选择不同大小的圆,使用绕绳法进行测量,获得数据,认真计算。最后,小组成员综合比较计算结果,得出结论:圆的周长是直径的3 倍多一些。
在实践操作后,该小组毛遂自荐,展示操作过程和结果。其他小组在观看、倾听时,结合本组的实践操作成果,提出其他方法。最终,全体学生依据操作结果,达成共识:圆的周长是直径的3 倍多一些。
在不知道圆的周长计算公式的情况下,学生动手操作,将未知的曲线(圆的周长)转化为可以度量的线段,利用已有知识探究、得到新知识,实现了有意义建构,切实地拓展了学习深度。
(二)在解决问题中应用转化思想
转化思想是学生解决问题的“工具”。尤其,学生掌握转化思想不是一件一蹴而就的事情,需要经过反复训练。教师要依据学生的数学学习情况,组织问题解决活动,促使学生应用转化思想解决数学问题,建构数学认知,内化转化思想,增强深度学习效果。
例如,在教学“多边形的面积”后,教师组织问题解决活动——求复杂图形的面积。在活动中,教师呈现题目:如图2 所示,ABCD是一个长方形,长12 cm,宽6 cm。E、F分别是AB、AD的中点。请问阴影部分的面积是多少?
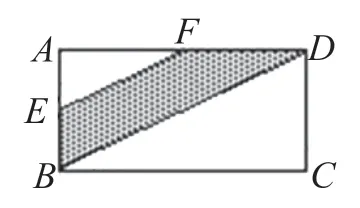
图2
教师鼓励学生合作解决问题。在合作的过程中,大部分学生边观察图像边动脑,发挥空间想象能力,依据问题条件,梳理思路,继而动手操作,解决问题。
有小组代表提出:“从E点出发,向对边作一条垂直线段;从F点出发,也向对边作一条垂直线段,此时得到四个大小相同的小长方形。”依据小组代表的思路,教师操作电子白板,展示相关内容(如图3)。
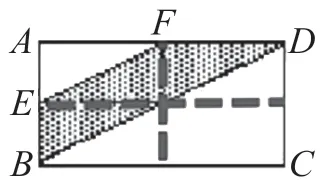
图3
小组代表据此继续介绍:“经过如此操作,阴影部分变成了三个大小相同的小三角形。”其他学生在倾听时主动发问:“怎样确定这三个小三角形大小一样?”小组代表对照图像,分析三个三角形的底和高的长度,给出“等底同高”的结论。接着,小组代表依据三角形的面积公式列出算式,得出所求阴影部分的面积。
在这个过程中,其他学生提出不同的看法。如“如此分割后,阴影部分是一个平行四边形和一个直角三角形。平行四边形的底是6 cm,高是3 cm,三角形的两条直角边分别是6 cm 和3 cm,根据平行四边形、三角形的面积公式,列出算式:6×3+6×3÷2=27 cm2。”
在问题解决的过程中,学生发挥空间想象能力,迁移已有数学认知,巩固了所学知识,运用了转化思想。教师把握时机,继续呈现类似的问题,驱动学生继续解决。通过不断解决问题,学生扎实掌握了转化思想,培养了空间观念、几何观念和数学运算能力。
四、结束语
总之,有效渗透转化思想,便于学生深度学习“图形与几何”的内容,建构知识体系,发展核心素养,增强学习效果。对此,在实施小学数学“图形与几何”教学时,教师可以依据“图形与几何”教学内容,挖掘转化思想,选用适宜的方式,促使学生体验知识生成活动和问题解决活动。在体验活动时,学生会积极思维,迁移已有认知,想象、操作,掌握数学知识,建构知识体系,同时发展数学学科核心素养。
