Time-fractional Davey-Stewartson equation:Lie point symmetries,similarity reductions,conservation laws and traveling wave solutions

Baoyong Guo,Yong Fang and Huanhe Dong

College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao,266590,China

Abstract As a celebrated nonlinear water wave equation,the Davey–Stewartson equation is widely studied by researchers,especially in the field of mathematical physics.On the basis of the Riemann–Liouville fractional derivative,the time-fractional Davey–Stewartson equation is investigated in this paper.By application of the Lie symmetry analysis approach,the Lie point symmetries and symmetry groups are obtained.At the same time,the similarity reductions are derived.Furthermore,the equation is converted to a system of fractional partial differential equations and a system of fractional ordinary differential equations in the sense of Riemann–Liouville fractional derivative.By virtue of the symmetry corresponding to the scalar transformation,the equation is converted to a system of fractional ordinary differential equations in the sense of Erdélyi–Kober fractional integro-differential operators.By using Noether’s theorem and Ibragimov’s new conservation theorem,the conserved vectors and the conservation laws are derived.Finally,the traveling wave solutions are achieved and plotted.

Keywords: time-fractional Davey–Stewartson equation,Lie symmetry analysis approach,Lie point symmetries,similarity reductions,conservation laws

1.Introduction

Nonlinear partial differential equations(NPDEs)usually play an indispensable role in revealing numerous physical phenomena in nature [1–9].In the last few decades,researchers have paid much attention to the study of NPDEs,including their dynamic properties and solutions.A number of methods were put forward to acquire the solutions of NPDEs,for example,the homogeneous balance method [10–13],inverse scattering transform [14–18],Darboux transformation[19–24],Hirota’s bilinear method [25–33],Riemann–Hilbert approach [34–43],nonlocal symmetry method and so on[44–49].However,for most NPDEs,the solutions are difficult to obtain due to their complex expressions.

As a generalization of classical calculus,fractional calculus is proposed by many researchers.Fractional derivative is an important concept of fractional calculus.The order of a fractional derivative can be an integer or a fraction,whereas the order of a classical derivative can only be an integer.The fractional derivatives used widely are Riemann–Liouville,Caputo and Grünwald–Letnikov types.For many applied disciplines,especially in fluid mechanics and materials science,compared with integer-order NPDEs,nonlinear fractional partial differential equations (NFPDEs) can be better used to explain natural processes and phenomena.This is because the systems corresponding to NFPDEs possess good time memory and global correlation,which can better reflect the historically dependent process of the development of system functions.Thus,the performance of the systems is improved.

The Lie symmetry analysis approach [50–59] is mainly used to find the similarity reductions and solutions of NPDEs.This method was originally utilized to investigate the continuous transformation groups in solving differential equations.This theory was proposed by Sophus Lie and has achieved fruitful development over the last few decades.Because this method can be used to find the group-invariant solutions of NPDEs,it has become a prominent approach to studying the properties of solutions of NPDEs.Since the Lie symmetry analysis approach is mainly used to study integerorder NPDEs,it has an important theoretical research value to extend the method to NFPDEs.Although this method is not widely used in NFPDEs,there are still many achievements in this respect [60–62].

This paper aimed to investigate Lie point symmetries,similarity reductions,conservation laws and traveling wave solutions for the time-fractional Davey–Stewartson (DS)equation.The DS equation is [63]

where x and y are spatial coordinates;t is a temporal coordinate;u=u(x,y,t) is a complex analytic function that represents the amplitude of wave;and v=v(x,y,t) is a real analytic function that can be treated as a forcing effect on the wave as it propagates.

The DS equation was proposed by Davey and Stewartson.It is a two-dimensional extension of the famous(1+1)-dimensional nonlinear Schrödinger (NLS) equation.In fluid dynamics,the DS equation describes the evolution of wave envelope in water waves and has wide applications.

If the Riemann–Liouville derivative operatoris introduced,the time-fractional DS equation reads as

where 0<γ<1 is the order of the Riemann–Liouville derivative.

This paper is organized as follows.In section 2,the definition and some properties of the Riemann–Liouville fractional derivative are described.In section 3,based on the Lie symmetry analysis method,the Lie point symmetries of the time-fractional DS equation are presented.In section 4,the similarity reductions of the time-fractional DS equation are obtained.Meanwhile,the original equation is converted to a system of fractional partial differential equations and two systems of fractional ordinary differential equations.In section 5,the conserved vectors and the conservation laws of the time-fractional DS equation are derived.In section 6,the traveling wave solutions are depicted and plotted.Finally,some main conclusions are presented.

2.Riemann-Liouville fractional derivative

Definition 1.Takex,yas spatial variables and t as a temporal variable,respectively,andn∊ N,γ∊+R,then for functionf=f(x,y,t),its γth-order Riemann–Liouville fractional partial derivative is

whereI γf(x,y,t)is the γth-order Riemann–Liouville fractional integral,and it is defined as

where Γ(γ)is the gamma function.

The properties of the Riemann–Liouville fractional derivative are

3.Lie point symmetries of the time-fractional DS equation

From equation (2),it can be seen that the time-fractional DS equation is a complex coupled system.To obtain the Lie point symmetries of the system,equation (2) needs to be transformed into a real coupled system.

First,we substitute the transformation u(x,y,t)=p(x,y,t)+iq(x,y,t)into equation(2).Consequently,equation(2)is transformed to the system as follows:

where p(x,y,t) and q(x,y,t) are real functions.

The general form of equation (5) (system) is in the following:

where 0<γ<1.

The one-parameter Lie group of transformations for equation (5) has the following form:

Taking vector field as follows:

therefore,the second prolongation of vector field V can be

By utilizing the Leibnitz rule of Riemann–Liouville derivative,equation (13) can be rewritten as

According to the derivation rule for composite function,for functions f=f(x) and f=g(x),one obtains

By utilizing the preceding results,one acquires

Substituting equation (15) into equation (14),one achieves

Substituting equations (12) and (16) into equation (11) and equating the coefficients of the partial derivatives and powers of the functions p,q and v with respect to the independent variables x,y and t be zero,then a system of determining equations is derived.Solving the determining equations,one has

where C1,C2,C3and C4are arbitrary constants.Therefore,the vector field V can be presented as

then the vector field V can be written as

and from that the following theorem is presented.

Theorem 1.The Lie algebraA,which is spanned byV1,V2,V3and V4,has the following commutation relations(table 1).

Where [Vi,Vj]=ViVj-VjVi.It is obvious to see that the Lie algebraA is closed.Consequently,the Lie point symmetries of equation (5) are generated by vector field V.

The symmetry groups can also be derived.The following theorem shows the result.

Theorem 2.If[p=p(x,y,t),q=q(x,y,t),v=v(x,y,t)]is a solution of equation (5),then

are also solutions of equation (5).

Proof.Assuming symmetry group Gisatisfies:

Consider initial value problem,which satisfies the conditions as follows:

where ε is a parameter.Soving equation (22) results in

Therefore,the solutions[p1,q1,v1],[p2,q2,v2],[p3,q3,v3]and[p4,q4,v4]can be derived. ☐

4.Similarity reductions of the time-fractional DS equation

In the preceding section,the Lie point symmetries are presented.With the help of these results,similarity reductions can be provided.

Table 1.Commutation relations of the Lie algebra A.

Taking similarity variables ξ=-lx+ky,η=t,and the group-invariant solutions

Substituting equation (24) into equation (5),one has

Selecting similarity variableand the groupinvariant solutions

Substituting equation (26) into equation (5),one has

III: The Erdélyi–Kober fractional integro-differential operators are powerful techniques for reducing fractional partial differential equations.In this part,the Erdélyi–Kober fractional integro-differential operators are utilized to reduce equation (5).

Choosing variable transformation

Therefore,equation (29) leads to

Repeating the preceding process n-1 times,one has

where the Erdélyi–Kober fractional integral operator is

and the Erdélyi–Kober fractional differential operator is

Substituting equations (31) and (32) into equation (5),one has

5.Nonlinear self-adjointness and conservation laws of the time-fractional DS equation

The conservation law is closely related to the integrability of NPDEs;therefore,it is an important aspect in the study of NPDEs.As is known to all,if an NPDE has N-soliton(N ≥3)solutions,it is integrable.This equation has infinitely many conservation laws.In addition,conservation laws can be used to reveal a number of physical laws.The three famous physical laws in nature,namely conservation of mass,conservation of momentum and conservation of energy,are all important representations of conservation laws.From this perspective,conservation laws link mathematical representations to physical laws skillfully.In recent decades,conservation laws have been studied widely by many researchers,and a large number of new natural laws and phenomena are explained.Many methods of constructing conservation laws have been presented.Among these achievements,Noether’s theorem and Ibragimov’s new conservation theorem are extensively used[64,65].In addition,making use of pairs of symmetries and adjoint symmetries,a general one-to-one correspondence between conservation laws and non-Lagrangian equations is established and has been applied to the computation of conservation densities of the nonlinear evolution equations,including heat equations,Burgers equation and Korteweg–de Vries equation [66].

5.1.Nonlinear self-adjointness of the time-fractional DS equation

Introducing new dependent variables α=α(x,y,t),β=β(x,y,t) and ζ=ζ(x,y,t) and taking

whereF is called formal Lagrangian.The action integral of equation (34) is

where (x,y,t)∊Ω1×Ω2×T.For equation (5),the adjoint equation is

where Γ(γ) is the gamma function.Introducing dependent variables Ξ1,Ξ2,Ξ3such that

Equation (36) is nonlinear self-adjoint if Ξ1,Ξ2,Ξ3are not all zeros,and there exists cij(1 ≤i,j ≤3) so that the following equation holds:

Combining equations (36),(37) and (38) leads to

Solving equation (39) results in

where F(t) is an arbitrary function of t.Consequently,equation (5) is nonlinear self-adjoint.

5.2.Conservation laws of the time-fractional DS equation

Next,on the basis of the presented results,the conservation vectors and the conservation laws of equation (5) can be constructed.

Definition 2.TakingV△=(Vx,V y,Vt),ifV△satisfies the following equation:

then V△is called the conservation vector of equation(5),and equation(41)is called the conservation law equation,where Dx,Dyand Dtare denoted as the total derivatives with respect to x,y and t,respectively.By using Noether’s theorem and Ibragimov’s new conservation theorem,the conserved vector can be obtained as

It is verified that equations(43)–(46)all satisfy equation(41).

6.Traveling wave solutions of the time-fractional DS equation

In this section,the traveling wave solutions of equation (5)can be provided.

For variable transformation

where n is a nonzero constant.Taking

where F and G are two real-valued functions,and

where k1,k2,k3,k4,k5and k6are nonzero real-valued constants to be determined.Equation (49) leads to

where the subscripts are denoted as the derivatives with respect to ξ.Substituting equation (50) into equation (5),one obtains

From the third equality of equation (52),one acquires

Substituting equation (53) into equation (52) comes

Integrating equation (55) with respect to ξ,one obtains

Equation (56) derives

Solving equation (57),one achieves

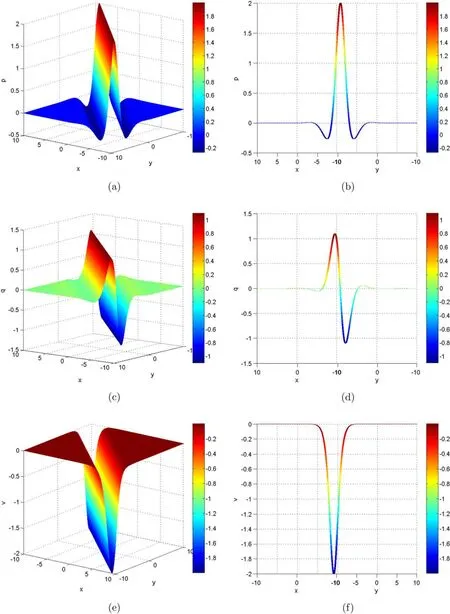
Fig. 1.(a) Three-dimensional drawing of the traveling wave solution p,(b) sectional drawing of p,(c) three-dimensional drawing of the traveling wave solution q,(d)sectional drawing of q,(e)three-dimensional drawing of the traveling wave solution v and(f)sectional drawing of v.The parameter values are taken as t=2,k1 =k2 =k3 =k4=k5 =k6=1,n=1 andγ=.

Fig. 2.(a) Three-dimensional drawing of the traveling wave solution p,(b) sectional drawing of p,(c) three-dimensional drawing of the traveling wave solution q,(d)sectional drawing of q,(e)three-dimensional drawing of the traveling wave solution v and(f)sectional drawing of v.The parameter values are taken as t=200,k1 =k2 =k3 =k4=k5 =k6=1,n=1 andγ=.

where k1,k2,k3,k4,k5and k6are nonzero real-valued constants.

Figure 1 shows the traveling wave solutions of p,q and v when the parameter values are taken ast=2,k1=k2=k3=k4=k5=k6=1,n=1 andγ=.In figure 2,t=200,and the values of the other parameters are the same as those in figure 1.It can be observed that when the waves of p,q and v propagate,their shapes and amplitudes remain the same.From sectional drawings(b),(d)and(f)in figures 1 and 2,it can be seen that the wave shapes of p,q and v have symmetry properties.It can also be seen that when x →∞or y →∞,the solutions p →0,q →0 and v →0.

7.Conclusions

In this paper,on the basis of the Riemann–Liouville fractional derivative,the time-fractional DS equation was investigated.By making use of the Lie symmetry analysis approach,the Lie point symmetries,symmetry groups,similarity reductions and traveling wave solutions were presented.For the first symmetry,the time-fractional DS equation was converted to a(1+1)-dimensional system of fractional partial differential equations.For the second symmetry,the equation was transformed into a system of fractional ordinary differential equations.Meanwhile,the equation can also be converted to a system of fractional ordinary differential equations in the sense of the Erdélyi–Kober fractional integro-differential operators.By application of Noether’s theorem and Ibragimov’s new conservation theorem,the conserved vectors and conservation laws were derived.Finally,the traveling wave solutions were deduced.The results profoundly revealed that the Lie symmetry analysis approach can be effectively applied to the theoretical research for NFPDEs.It should also be interesting to see if traveling wave solutions could be similarly determined for nonlocal integrable equations,for example,nonlocal NLS models [67].

Acknowledgments

The authors would like to thank all editors and reviewers for their comments to the improvement of this paper.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.11975143).

Declaration of interest

The authors declare that they have no conflicts of interest.