Security control of Markovian jump neural networks with stochastic sampling subject to false data injection attacks★
2023-10-11LanYaoXiaHuangZhenWangandMinXiao
Lan Yao,Xia Huang,Zhen Wang and Min Xiao
1 College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China
2 College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
Abstract The security control of Markovian jumping neural networks(MJNNs)is investigated under false data injection attacks that take place in the shared communication network.Stochastic sampleddata control is employed to research the exponential synchronization of MJNNs under false data injection attacks (FDIAs) since it can alleviate the impact of the FDIAs on the performance of the system by adjusting the sampling periods.A multi-delay error system model is established through the input-delay approach.To reduce the conservatism of the results,a sampling-periodprobability-dependent looped Lyapunov functional is constructed.In light of some less conservative integral inequalities,a synchronization criterion is derived,and an algorithm is provided that can be solved for determining the controller gain.Finally,a numerical simulation is presented to confirm the efficiency of the proposed method.
Keywords: Markovian jumping neural networks,stochastic sampling,looped-functional,false data injection attack
1.Introduction
The Markovian jump system (MJS) is a class of special switched systems,that can describe various emergencies that occur in industrial systems.An MJS has multiple working modes and it will switch among these modes based on a Markov chain.Because MJSs can reflect the characteristics of jump among different system modes,which greatly overcomes the limitations of a single system,it has great flexibility in simulating practical engineering systems.MJSs are widely used in satellite systems,image processing,security communications and other fields.Under this background and trend,the study of MJSs has important practical significance and practical value for modeling practical systems with finite modes.In the past decades,many outstanding achievements have been gained [1–3],including stability,synchronization,and filtering.In addition,chaotic synchronous communication is currently a hot research topic internationally [4,5].Markovian jumping neural networks (MJNNs) have broad application prospects in the fields of image encryption and audio encryption by utilizing the chaos synchronization of MJNNs,which has been widely discussed in [6–10].
With the ongoing advancements in digital control technology,sampled-data control (SDC) has gained extensive development in [9–14],which can effectively solve the problem of data redundancy.However,due to the openness of communication networks,SDC systems are vulnerable to malicious cyber attacks [15–17],which may degrade the system performance or even compromise the stability of the SDC system.Therefore,the security control problem of SDC systems has been widely discussed by researchers.There are many types of cyber attacks,mainly including deception attacks [18–21],DoS attacks [22],and false data injection attacks(FDIA)[23–25].Therein,FDIA,as a common type of attack,can destroy the integrity of communication data by sending error information to the receiver,thus causing unpredictable damage to the SDC system.In[23],the security problem for the state estimation of the networked control system was discussed by proposing a specific algorithm of generating attacks to estimate the insecurity of the system.In[24],the stability of switched semi-MJSs was investigated under the FDIAs by using a reduced-order sliding mode control.Following this trend,it is a key issue to design appropriate mechanisms to alleviate the impact of attacks,which motivates our present research.
On the other hand,non-ideal network environments can bring about unpredictable network phenomena,such as time delay and sampling errors,which will inevitably lead to the jitter of the sampling period.To address this problem,the stochastic sampled-data control (SSDC) method has been proposed in [26].SSDC allows the existence of multiple sampling periods with certain occurrence probability,that is,it allows the sampling period to jitter to a certain extent.Therefore,the SSDC can not only adjust the sampling period more flexibly to cope with the sampling error,but also alleviate the impact of cyber attacks on the performance of the controlled system.Hence,SSDC has attracted extensive attention [26–28].Unfortunately,there are few works on the study of security control of MJNNs under FDIA via SSDC,which motivates the research of this article.
Recently,the looped Lyapunov functional (LLF) technique has been extensively employed for analyzing the stability of SDC systems [29–32].Unlike the traditional Lyapunov functional,LLFs replace the positive definitiveness restriction with a loop condition.That is to say,the LLF relaxes the requirement for the functional to be positively definite in the sampling interval.Therefore,the conservatism of the obtained results can be relaxed by using the LLF method.In addition,LLF has the ability to fully utilize the state information of the sampled data system.However,the construction of LLFs for MJNNs subject to cyber attacks and stochastic sampling is difficult.Hence,the primary objective of this article is to develop an LLF and the corresponding analysis method for exponential synchronization of MJNNs via stochastic sampling.
Summarizing the aforementioned considerations,the security control of MJNNs under the FDIAs is investigated by using LLF,and the main contributions are threefold:
(1) To alleviate the impact of FDIA on the performance of the MJNNs,SSDC is developed to investigate the security control of the controlled system;
(2) The model of the error system with multi-delays is established.Associated with it,a sampling-period-probability-dependent LLF is constructed to reduce the conservatism of the main results.
(3) A less conservative exponential synchronization criterion and a design algorithm for determining the controller gain are given,respectively.
Notations:DenotenR be the n-dimensional Euclidean space.Let* and In(0n) be the symmetric entries in a symmetric matrix and n-dimension identity (zero) matrix,respectively.QT,Q-1,Sym{Q} and Q>0 denote the transpose,inverse of matrix Q,Q+QTand the symmetric and positive definite matrix,respectively.diag{…} and col{·}denote the diagonal matrix and column vector.Prob{X} and E {·}denote the probability and the mathematical expectation of event,respectively.λmin(λmax)and max {m,n}refer to the maximum (minimum) eigenvalue and the largest value of m and n,respectively.(Ω,F,P) represents the complete probability space.
2.Problem description
The schematic diagram of the security control of MJNNs under FDIAs occurred in the communication network channel is shown in figure 1.In figure 1,the sensor transmits the sampled data by stochastic sampling.
In figure 1,the time-varying delayed master-slave MJNNs can be described as:
Let r(t)=s(t)-m(t) be the state error of the master and slave system,then the corresponding error system can be represented as:
where ϖ(r(t))=χ(s(t))-χ(m(t)),ϖ(r(t-τ(t)))=χ(s(t-τ(t)))-χ(m(t-τ(t))) and
Represent the set of sampling instants as{tk}k∊N.For t ∊[tk,tk+1),the SSDC-based controller is designed:
where K represents the gain matrix of the controller that requires designing later.
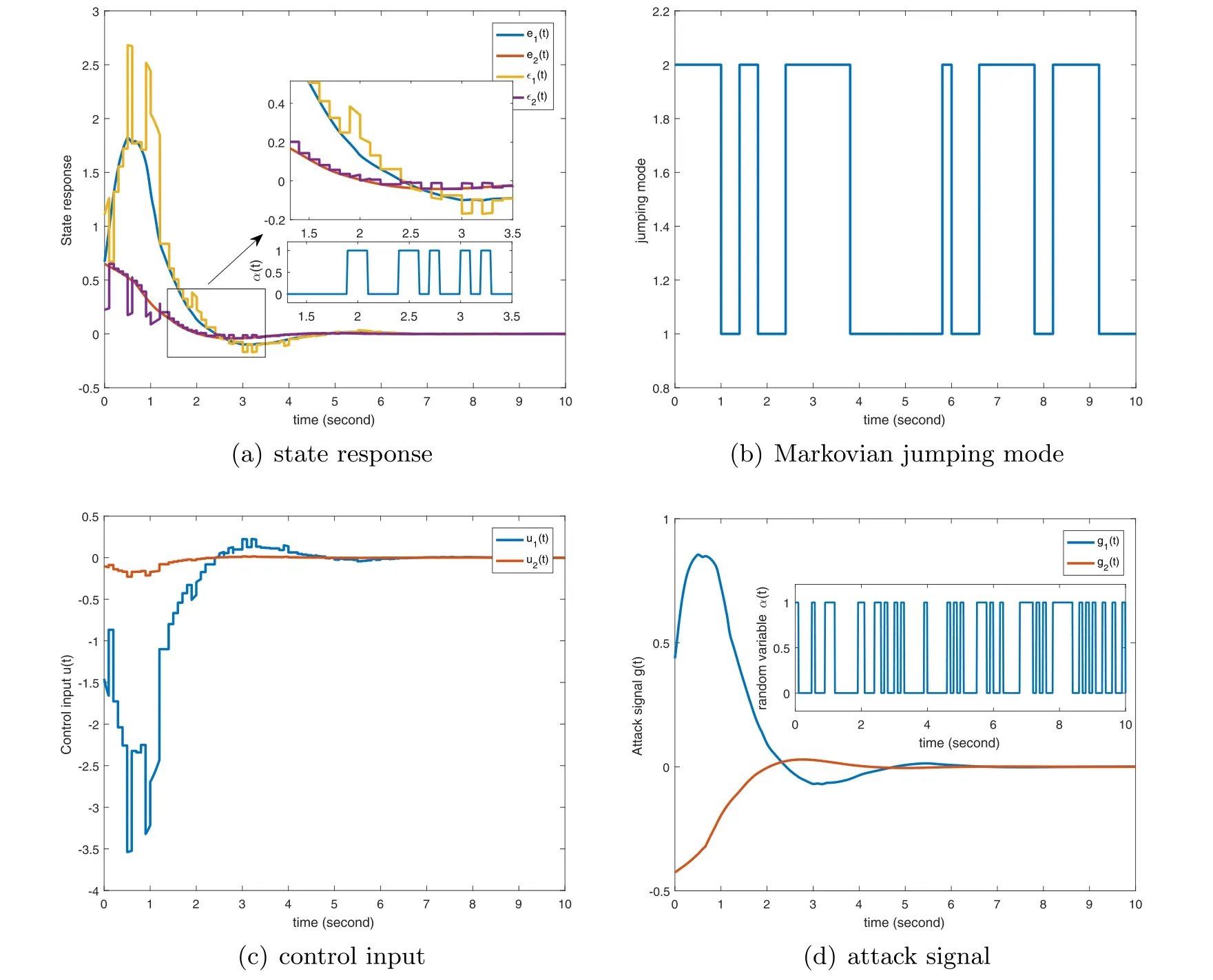
Thus,the occurrence probability of the event hj-1≤d(t) To quantify the above events,for j=1,…,m,total 2m random variables satisfying Bernoulli distribution introduce: Then,we can calculate that Because the FDIAs occurred in the network channel randomly,the random attack can be described by introducing the random variable α(t): In addition,due to the attack signal g(t) is limited by the attack energy,Assumption 2 is needed. Assumption 2.For g(t),suppose there exists constant matrix G satisfying Then,the signal transmitted to the controller can be rewritten: Thus,the control input under the FDIAs is expressed as Combining (2) with (5),the closed-loop system (2) can be represented: Remark 1.Note that different from the deterministic SDC,SSDC has multiple sampling periods,which can reflect the inherent characteristics of the sampling error.Hence,the SSDC system can not only ensure the system achieves the desired performance in a nonideal environment,but also reduce the redundancy of communication transmission.In light of the characteristics of SSDC,the position of dj(t) can be described by introducing a series of random variablesγ j(t),which follow the Bernoulli distribution. Remark 2.In an unsatisfactory network environment,attackers tamper with the transmission data by launching FDIAs to destroy system performance.In view of the randomness of the cyber attack,the data transmitted to the controller can be given byε(t) with random variableα(t).Under the FDIAs,SSDC can alleviate the impact of the attacks on the performance of the controlled system by adjusting the occurrence probability of the sampling periods. For simplicity,The following symbols will be utilized: Proof.The time-dependent LLF is constructed as follows: For V4(t) and V5(t),through analyzing the characteristic of (tk+1-t)-terms,V4(t) and V5(t) can be expressed with multi-delays as Calculating LV j(t) (j=1,2,…,5) along the trajectories of the error system (6),we have For V2(t),we have Combining with the less-conservative integral inequality[32],we have Then,combining the above inequality,we have Combining with the Jensenʼs inequality and the reciprocally convex inequality [34],the second integral term inLV3(t) is estimated: where φ(t)=col{r(t-τ1)-r(t-τ(t)),r(t-τ(t))-r(t-τ2)}. Thus,LV3(t) can be estimated as For the activation function ϖj(·),the following two inequalities hold: this means that for Λ1>0 and Λ2>0,the two inequalities hold: The inequalities (13) and (14) are equivalent to Additionally,combining with the error system (6),for matrices M1,M2,the following equation holds: Then,for t ∊[tk,tk+1),i∊ R,combining inequalities(10)–(17),we obtain that Integrating the error system (6) from tkto t,we have Thus,combining with the Gronwall-Bellman inequality[36],we can conclude Furthermore,based on the inequalities (13)–(14),we obtain From the inequality given above,we can conclude Hence,the master-slave MJNNs (1) achieve exponential synchronization via controller (5) under FDIAs.That completes the proof. Remark 3.In this paper,the time-dependent loopedfunctionalW(t) is constructed.FromW(t),we can easily see that the positive definiteness of the functional matricesUj,Vj,Xjare not required.That is,W(t) relaxes the positive definite constraint ofW(t) in the sampling interval,and only requires its positive definiteness at the sampling instants{tk},it contributes to relaxing the conservativeness of the stability conditions and to increasing the maximum allowable bound of the sampling intervals. Fig. 2.(a) The time response of r(t) and ε(t);(b) Markov jumping mode;(c) the control input;(d) the attack signal g(x(t)) and α(t). Table 1.The maximum value of h2 for different h1 with β1=0.6,β2=0.4,δ=0.5. Remark 4.Significantly,theβ j(t)-dependent LLFW(t)contains the information of occurrence probabilityβjfor different sampling periods,thus,the derived synchronization conditions areβj-dependent.When facing cyber attacks,we can adjustβjto obtain an appropriate control gain K. Consider the system parameters of a MJNN proposed in[6]as follows: C1=diag{1,0.9},C2=diag{1,1},π12=0.5, Table 2.The maximum value of h2 for different β1 with δ=0.1,h1=0.1. Table 1 gives the maximum bound of h2for different h1and α with β1=0.6,β2=0.4,δ=0.5.From table 1,it is easy to see that the maximum value of h2becomes larger gradually with the decrease of h1.In addition,when h1is fixed,with the increase of the attack probability α,the maximum value of h2is smaller.Table 2 provides the maximum value of h2for different β1when h1and α are fixed.It is easy to see from table 2 that the maximum value of h2becomes smaller gradually with the decrease of β1. Specify the values of the parameters in theorem 2 as α=0.4,δ=0.1,β1=0.6,h1=0.1,h2=0.2,λ=0.3.The solution that satisfy the LMIs (23) of matrix K is solved via MATLAB LMI Toolbox as: By using the parameters mentioned above,the time response of the error system state r(t)and the transmitted data ε(t),the control input and the FDIA signal g(x(t)) with occurrence probability α(t) are demonstrated in figure 2.From figure 2(a),we can see that system (1) can reach exponentially synchronized by the SSDC (2),which demonstrates the effectiveness of the designed controller in mitigating the FDIAs. The security control of master-slave MJNNs has been investigated via SSDC and LLF subject to FDIAs in this paper.SSDC can not only solve the problem of data redundancy,but also mitigate the impact of FDIAs on the system performance.An error system model is established with multi input-delays.Then,a βj(t)-dependent LLF is constructed to reduce the conservativeness of the synchronization condition(i.e.theorem 1).On this basis,an easy-to-solve design algorithm for SSDC is given (i.e.theorem 2).Finally,through a numerical example,it is verified that SSDC can realize the exponential synchronization of MJNNs under FDIAs,and this SSDC synchronization method has been applied to image encryption and decryption successfully. ORCID iDs3.Main results

4.Numerical example

5.Conclusions
杂志排行
Communications in Theoretical Physics的其它文章
- Electromagnetic effects on anisotropic expansion-free fluid content
- From decoupled integrable models tocoupled ones via a deformation algorithm*
- Lyapunov functions for studying global asymptotic stability of two rumor spreading models
- Investigation of the Rayleigh-Taylor instability in charged fluids
- The effect of different generalized uncertainty principles on Jeans mass modification
- Gravitational quasinormal modes of a parametrized Schwarzschild metric
