基于优化星座图的MIMO雷达-通信一体化发射波形设计

黄 超, 黄中瑞, 周青松, 张剑云

(国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引 言

近年来,随着电子信息技术的不断进步,不同电子设备对频谱的需求不断增长,尤其是雷达和通信系统之间的频谱竞争愈发激烈。为解决雷达与通信系统的频谱拥塞问题,雷达通信频谱共享(radar and communication spectrum sharing, RCSS)[1-2]技术受到了学术界的广泛关注。当下,RCSS技术主要包括两个研究方向。一是雷达与通信频谱共存(radar communication coexistence, RCC)[3-4],主要采用频谱赋形和频谱动态管理等技术来实现同一频段内雷达和通信系统的独立共存;二是雷达通信一体化(dual functional radar communication,DFRC)[5-9]。相比RCC,DFRC共享硬件平台、空间频谱、发射波形等系统资源,能够更好地提升系统资源利用效率,是国内外相关研究人员解决频谱拥塞问题的首选方案。

DFRC系统实现雷达和通信双功能的关键是一体化发射波形设计。根据应用场景和设计优先级的不同,DFRC一体化发射波形设计可分为以雷达为中心[10-15]、以通信为中心[16-19]和联合优化设计[20-25]。其中,以雷达为中心的DFRC系统,由于其通信功能可以共享雷达的高发射功率和强方向性,在通信信息传输的保密性和抗干扰性上更具优势。因此,本文重点关注以雷达为中心的DFRC发射波形设计。

2014年,法国学者Euziere等[26]率先提出基于时间调制阵列(time modulated array, TMA)的DFRC波形设计方法。该方法通过对不同时间片段内指定通信方向的旁瓣电平进行差异化设计,采用幅移键控(amplitude shift keying,ASK)的方式实现通信信息传输。但由于这种DFRC系统是在传统相控阵雷达基础上进行设计的,发射波形优化自由度不高,在发射波束控制、传输信息调制等方面存在较大的局限性。

多输入多输出(multiple input multiple output, MIMO)雷达具有独特的发射波形分集优势,与传统相控阵雷达相比,发射方向图设计更加灵活。因此,结合MIMO雷达和DFRC系统的优势,围绕MIMO-DFRC系统的发射波形设计展开研究,已经成为了时下的热点研究问题。

MIMO雷达-通信一体化波形设计的核心关键就是选取适合的通信信息植入策略。其中,较为经典的方法有如下几种。文献[27-28]提出基于波形分集和旁瓣控制的DFRC波形设计方法,由于该方法利用了MIMO雷达的波形分集优势,能够放松对旁瓣电平的苛刻设置要求。与TMA算法相比,在通信信息传输速率一定的前提下,误码率(bit error rate,BER)性能得到了有效改善。文献[29-31]进一步提出基于相移键控(phase shift keying, PSK)和正交幅度调制的(quadrature amplitude modulation, QAM)的MIMO-DFRC发射波形设计算法。与采用幅度调制法相比,后两种方法的优化自由度更高,具有更加优越的通信信息传输BER性能。

然而,无论上述文献如何设计通信信息植入策略,仍然需要使用常见的ASK、PSK和QAM等信息调制方法来设计通信星座图。由于优化自由度的限制和调制模式的固定,基于传统通信星座图的MIMO-DFRC发射波形设计很难获取最优的通信传输BER性能。

对此,本文提出了基于优化星座图的MIMO-DFRC发射波形设计方法。首先,构建了MIMO-DFRC系统的发射波形优化设计模型;其次,基于通信信号幅度和相位联合约束设计了通信信息植入策略;同时,为了降低通信传输BER,进一步对期望通信信号的星座图进行了优化设计;最后,仿真分析验证了本文所提方法的有效性。

1 信号模型

假设MIMO-DFRC系统由一个双功能发射阵列、一个雷达接收阵列和一个通信接收机组成。发射阵列和雷达接收阵列都是均匀线阵,分别包含M个发射阵元和N个接收阵元,阵元间距均为半波长。通信接收机位于发射阵列θc方向,包含一个基波形匹配滤波器组,可以对通信接收机接收的信号进行匹配滤波。DFRC系统的结构示意图如图1所示。

图1 MIMO-DFRC系统结构示意图Fig.1 Structure diagram of MIMO-DFRC system

令发射阵列的发射信号矢量为x(t;τ)=[x1(t;τ),x2(t;τ),…,xM(t;τ)]T,x(t;τ)的表达式为

x(t;τ)=Ws(t;τ)

(1)

式中:t表示快时间索引;τ表示慢时间索引,即脉冲索引;W=[w1,w2,…,wK]为M×K维的波束加权矩阵;s(t;τ)=[s1(t;τ),s2(t;τ),…,sK(t;τ)]T是由K个正交基波形组成的基波形向量,相互之间满足如下关系:

(2)

式中:Tp为脉冲宽度,基波形具有理想的自相关特性。

根据式(1)可以给出远场空间任一方向θ处的发射信号为

y(t;τ)=aH(θ)x(t;τ)=aH(θ)Ws(t;τ)

(3)

式中:a(θ)=[a1(θ),a2(θ),…,aM(θ)]T为发射导向矢量,且am(θ)=exp(jπ(m-1)sinθ)(m=1,2,…,M)。

通信接收机接收信号为

zc(t;τ)=βc(τ)aH(θc)x(t;τ)+nc(t;τ)

(4)

2 发射方向图优化

MIMO-DFRC系统的主要任务是对空间目标进行探测(即雷达功能),次要任务是与θc方向处的通信接收机完成通信信息传输(通信功能),并且不影响其目标探测功能。

根据式(3)可以得到发射信号在空间的功率分布为

P(θ;τ)=E{aH(θ)Ws(t;τ)(aH(θ)Ws(t;τ))H}=
aH(θ)WWHa(θ)

(5)

式(5)利用了基波形的正交性,即

E{s(t;τ)sH(t;τ)}=IK

(6)

为了提高一体化系统的目标检测性能,需确保发射信号在感兴趣空域形成聚焦波束,同时在旁瓣区域尽可能减小辐射功率。因此可以给出波束加权矩阵的优化模型为

(7)

式中:Θm′和Θs分别表示方向图的主瓣和旁瓣区域;θm′和θs分别为相应的离散化角度,离散化个数分别为M′和S;d(θm′)表示主瓣区域的期望波束;σ是方向图匹配误差门限。

式(7)仅仅从雷达目标探测方面对发射方向图进行了优化,并没有考虑通信信息的传输。为了实现通信信息传输功能,需要对通信接收机方向的辐射信号进行特殊设计。从目前文献的研究可知,一般基于MIMO平台的波形分集特性,从方向图在通信接收机方向上的辐射功率、信号相位以及发射阵列的阵元选择等方面进行考虑。为提高优化自由度,本文联合优化通信接收机方向辐射信号的幅度和相位,参考文献[27],构造MIMO-DFRC系统的发射波束加权矩阵优化模型如下:

(8)

式中:W=[w1,w2,…,wK],wK表示在空间形成第K个基波束所需的加权向量;δk是一个复数,表示发射信号在通信接收机方向形成的辐射信号。为了实现DFRC系统的目标探测和通信信息传输双重功能,要求不同wk形成的基波束在感兴趣空域保持不变,在通信接收机方向具有特定差异(δk随着k的不同而变化)。

式(8)是一个非凸问题,现有方法难以快速解决此问题。为此,本文将转而求解其松弛问题,优化模型如下:

(9)

式中:E=[φ(θ1),φ(θ2),…,φ(θM′)]T,φ(θm′)(m′=1,2,…,M′)是人为设置的参数。式(9)可以采用循环优化算法进行求解。

3 通信信息植入

通信信息植入策略是MIMO-DFRC发射波形设计的关键步骤,不同信息植入方法的选择决定了通信传输性能的质量。其核心思想是利用发射波形的分集特性和通信接收机方向上不同辐射信号之间的差异性来完成通信信息植入。为便于描述,进一步推导式(4)为

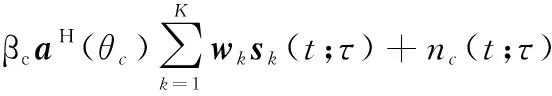
(10)

将通信接收机接收到的信号与每一个发射基波形进行匹配滤波,可以得到

(11)

为最大化空间自由度,本文联合调制基波形在通信接收机方向合成辐射信号的幅度和相位信息,进行通信信息植入。首先,在每个雷达脉冲重复周期内,总共设计K组波束加权向量w1,w2,…,wK,通信接收机方位的合成辐射信号为aH(θc)w1,aH(θc)w2,…,aH(θc)wK。选取第一个合成辐射信号作为参考信号,其他信号与参考信号的幅度和相位差可以表示为

(12)

通过设计波束加权矩阵W=[w1,w2,…,wK],获取K-1个不同的Akejφk,将需要传输的通信信息与Akejφk一一对应,并设计相应的通信星座图,即可在雷达发射波形中植入通信传输信息,植入的通信信号可表示为C=[A2ejφ2,A3ejφ3,…,AKejφK]。

4 通信星座图优化设计

4.1 问题提出

通信植入策略选定后,设计合适的通信星座图可以使MIMO-DFRC系统获取更好的通信传输BER性能。常见的通信星座图通常基于ASK、PSK和QAM调制方法进行设计,但它们并不能保证通信传输BER最小。为此,本文以获取更优的通信传输BER为目标,提出一种新的通信星座图优化设计方法。

为便于描述和直观理解,将预先植入的通信传输信号集C重新表述为C=[c1,c2,…,cL],L=K-1。同时进一步对其进行归一化处理,并画出其几何分布示意图,具体如图2所示。其中,各个离散分布的点ci、cj均为2×1维的实向量,分别代表C中各通信传输信号,‖ci-cj‖(i=1,2,…,L;j=1,2,…,L;i≠j)表示任意两个通信传输信号之间的欧式距离。

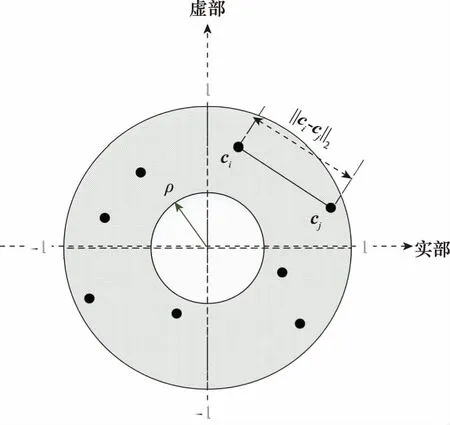
图2 C中各元素归一化分布示意图Fig.2 Normalized distribution skematic diagram of C

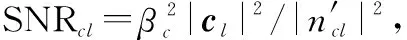
综上,本文以最大化C中任意两个元素欧式距离集合的最小值为优化准则,构建通信星座图的优化设计模型:

(13)

式中:约束条件中ρ≤|cl|≤1表示求解问题的优化可行域(即图2中阴影圆环部分)。显然,在式(13)的优化模型中,目标函数处于高维空间上,而且优化可行域是一个圆环,无法利用现有优化方法直接进行高效优化求解。

为方便后续求解,首先对问题优化模型进行一系列等价形式变换。令t=min ‖ci-cj‖2,将式(13)改写为

(14)

对式(14)中的两个不等式约束条件进行平方变换,可得到新的优化模型如下:

(15)

式(15)依然是非凸的。对此,本文提出了一种基于一阶泰勒展开的序列线性规划算法(sequential linear programming algorithm based on first-order Taylor expansion, SLP-FTE)进行优化求解。

4.2 SLP-FTE

首先,在可行域圆环ρ≤|cl|≤1内随机生成一个初始通信传输信号集合C0=[c01,c02,…,c0L]T。然后,依据初始值C0,直接求出其中任意两个点欧式距离集合的最小值t0。将式(15)中在C0和t0处进行泰勒展开,优化模型(15),可重新近似表达为

(16)

利用求解结果对C0进行迭代更新,可得到新的通信信号集合C1=[c11,c12,…,c1L]T。重复上述步骤,直至算法达到预先设置的收敛条件(Δt≤η,其中η是人为设置的收敛参数),算法终止。具体算法流程如算法1所示。

算法 1 SLP-FTE初始化:令n=0;在可行域ρ≤|cl|≤1内设置初始通信符号集合Cn=[cn1,cn2,…,cnL]T,则Cn中任意两个点欧式距离集合的最小值为tn;更新迭代:(1) 将Cn和tn代入式(16)中的优化模型,并利用内点法求解Δt和ΔC;(2) 根据求解结果,对C和t进行更新迭代,Cn+1=Cn+ΔC,tn+1=tn+Δt;(3) n++,重复上述步骤;迭代停止:当满足收敛条件Δt≤η时,算法终止。

5 通信信息解译

(17)

(18)

对照预先设计的通信传输星座图,即可解译相应的通信数据信息。对通信误码率(bit error rate, BER)、通信传输速率、应用场景有如下说明。

(1) 通信BER:假设在每个雷达脉冲重复周期内,一体化系统共发射L个基波形,其中有1个基波形作为参考波形,其余L-1个基波形传输通信信息,每个基波形能够携带Q比特通信信息。通过对匹配滤波后的所有通信接收信号进行估计,共有P比特通信信息估计错误。则本文方法的通信BER可表示为

(2) 通信传输速率:由式(1)可知,在每个雷达脉冲重复周期内,本文方法共计可以传输(L-1)×Q比特通信信息,则通信传输速率可表示为(L-1)×Q×fPRF,其中fPRF表示脉冲重复频率。目前,毫米波雷达的fPRF可以达到数十kHz。因此,当fPRF=50 kHz、L=6、Q=4时,本文方法的通信传输速率可以达到1 Mbps,与文献[27-31]中方法的通信传输速率相当。

(3) 应用场景:本文方法主要通过优化调整MIMO雷达波束旁瓣的幅度和相位来传递通信信息,不独立设计通信波束,通信传输很难抑制非视距信道的强多径干扰,一般只适用于视距信道下的下行链路通信。

6 仿真实验

假设MIMO雷达-通信一体化系统的发射阵列是均匀线阵,配备10个天线阵元,且天线阵元间距均为半波长:d=λ/2。将整个空域角度[-90°,90°]划分为181个网格点,雷达感兴趣的目标探测空域为[-10°,10°],通信接收机方位为40°。下面,分别从发射波束形成、通信BER和算法收敛性3个方面对本文方法具体展开分析。

6.1 发射波束形成性能

首先设置预期发射方向图中参数d(θm′)和σ分别为1和0.08,发射方向图旁瓣比主瓣低20 dB。为验证本文所提方法的发射波束形成性能,以传输2比特通信信息为例,采用本文通信信息植入方法,优化设计得到通信接收机方向的5个合成辐射信号分别为:0.1,-0.334 8-j0.942 3,0.334 8+j0.942 3,-0.942 3+j0.334 8和0.942 3-j0.334 8(其中第一个为参考信号)。

图3给出了MIMO-DFRC系统的发射功率方向图。

由图3可以看出,本文方法实现了发射功率在雷达感兴趣空域的有效聚焦,这为低信噪比下的雷达目标探测提供了有利条件。同时,由不同波束加权向量合成的发射波束在通信接收机方向存在预先设定的差异,这为通信信息植入奠定了良好基础。另外,通信接收机方向的合成方向图相比其他旁瓣区域未发生明显变化,这说明通信传输具有较好的保密性。

6.2 通信BER性能分析

下面,进一步对本文方法的通信传输BER性能进行分析比较。首先,定义通信接收机端信噪比(signal to noise ratio, SNR)为:通信接收机接收信号功率与噪声功率的比值。为便于对比分析,设置通信符号归一化幅度最小值ρ=0.1,发射基波形数目为2(其中1个为参考波形),假设每个基波形在每个雷达脉冲重复周期内传输Q比特通信信息。设置通信验证数据的序列长度为106,并重复进行100次蒙特卡罗试验。

当Q=2时,图4给出了采用本文方法设计的通信星座图,与QPSK设置的星座图相比,通信星座符号幅度相同,只是相位发生了一定的旋转。图5给出了通信BER性能分析。

图4 通信星座图(Q=2)Fig.4 Communication constellation diagram(Q=2)

图5 通信BER随SNR的变化(Q=2)Fig.5 Communication BER via SNR(Q=2)

由图5可以看出,QPSK和本文方法的通信BER性能随SNR的变化情况近乎完全一致,且明显优于文献[27]中的ASK方法。显然,QPSK方法是本文方法的特殊情况,当Q取值较小时,本文方法会退化为QPSK方法。

图6、图7分别给出了当Q=4时本文方法设计的通信星座图分布以及通信BER随SNR的变化。

图6 通信星座图(Q=4,ρ=0.1)Fig.6 Communication constellation diagram(Q=4,ρ=0.1)

图7 通信BER随SNR的变化(Q=4)Fig.7 BER via SNR(Q=4)

可以看出,本文方法的通信BER要明显低于文献[27]、文献[29]和文献[31]中的通信BER。这是因为,与基于16ASK、16PSK和16QAM等方法设计的通信星座图相比,本文方法设计的通信星座图分布更加稀疏,其中任意两个通信符号的最小欧式距离为0.553 2,明显优于16ASK的0.133 3以及16PSK、16QAM的0.382 7,这说明本文方法的通信信息传输受噪声扰动影响最小。

6.3 算法收敛性分析

图8给出了本文SLP-FTE算法的收敛性分析。

图8 收敛性分析Fig.8 Convergence analysis

由图8可以看出,仅需6次迭代,优化目标值t就已趋于稳定,得到了较好的通信星座图分布。

7 结 论

本文提出一种基于优化星座图的MIMO-DFRC发射波形设计算法。首先,构建了MIMO-DFRC系统的发射波形优化设计模型;其次,调制了通信接收机方向每个合成基波束相对参考信号的幅度和相位差,从而在MIMO雷达发射波形中植入了通信传输信息。最后,为提升通信传输BER性能,在考虑通信接收机检测门限和噪声扰动的基础上,进一步提出了SLP-FTE,以设计最优的通信星座图。仿真结果表明,本文方法设计的发射波形可以实现指定空域功率聚焦,能够在完成雷达目标探测的同时实现通信信息传输,在通信传输速率和SNR等相同的前提下,本文方法的通信传输BER比文献[27-31]更低。但是,本文在考虑通信接收机的有效检测问题时,只是简单地设置了一个SNR检测门限,并未考虑更加复杂的应用场景。对此,后续将进一步展开研究。