变形监测网稳定性分析与数据维护的关键技术
2023-10-11苏秀永马向阳
苏秀永,胡 航,马向阳
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.浙江华东测绘与工程安全技术有限公司,浙江 杭州 310014)
变形监测网点多布设于变形影响区外稳定位置,有条件的又分基准网和工作基点网,基准网远离变形影响区,工作基点网则在变形影响区周边,方便日常变形监测工作开展。然而,受区域地质构造和地球物理环境影响,各监测网点随时间推移仍会发生不同程度的位移,这些位移使日常变形监测工作产生误判、甚至诱发安全事故,因此定期复测监测网并进行监测网点稳定性分析与数据维护尤为必要。大量实践表明,采用全站仪、水准仪和规范的作业方法复测监测网的观测数据能达到毫米级精度。监测网属于起算数据不足的自由网,如何正确处理监测网复测数据,自20 世纪60 年代以来一直是国内外测量和形变分析研究的课题。周江文[1]于1980 年提出了拟稳平差,既有明确的测量根据,可为监测网提供前后变化比对的基准面;又没有强制附和,可保持网形不被扭曲,得到所需的准确信息。欧吉坤[2]等通过分析形变位移场和比较经典平差、伪逆平差,验证了监测网采用拟稳平差的必要性和优越性。拟稳平差的关键是选取符合实际的拟稳点[3]。在监测网点稳定性事先未知的情况下,王海城[4]等利用平均间隙法和t检验法对沉降监测基准点稳定性进行了验证,两种方法具有一致性;吴杰[5]等针对变形监测网点位异常问题提出了稳定性检验方法,并通过实例证明了在平均间隙法的基础上采用限差法和t 检验法对剩余稳定点重新进行稳定性检验的必要性;梁丽芳[6]讨论了拟稳点选取的两种方法,并举例说明了拟稳点法在实际沉降观测数据处理中的应用。
1 拟稳平差、平均间隙法和限差法
1.1 拟稳平差的原理和性质
以前次平差结果为近似值,结合本次观测数据进行有特类值的拟稳平差,顾及了监测网点可能不稳定的现状,变动相对较小的(即相对稳定)点,称为拟稳点[7]。设X0为拟稳点,X1为变动较大的点,则监测网误差方程为:
式中,V为改正数;A为误差方程系数矩阵;为参数估值;l为自由项;n为观测值个数;t为未知参数个数。
在最小二乘VTPV=min 原则下,由式(1)组成的法方程为:
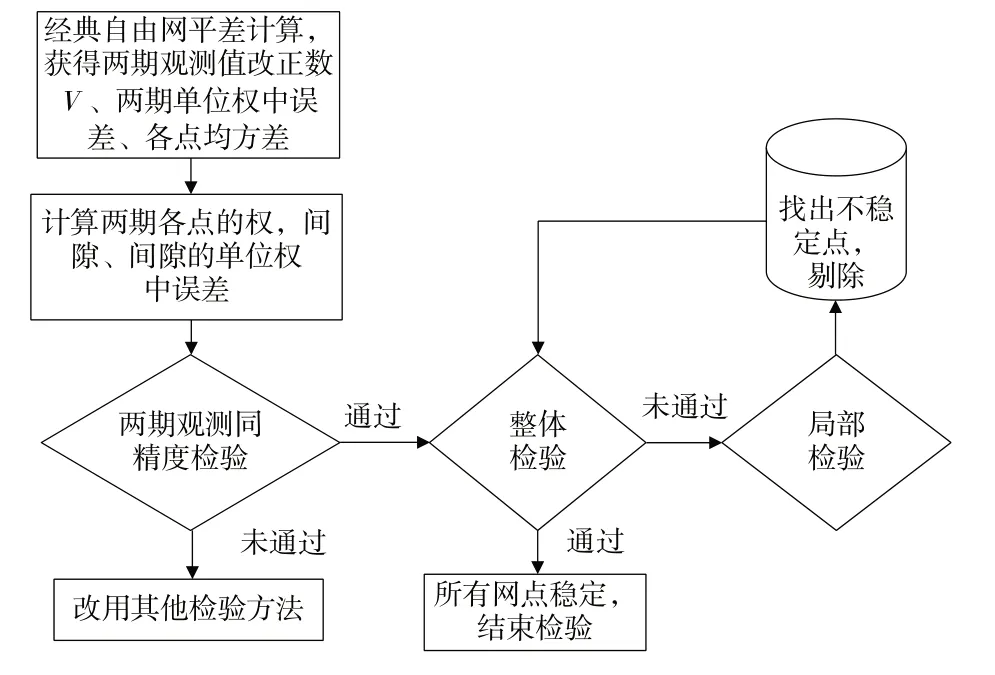
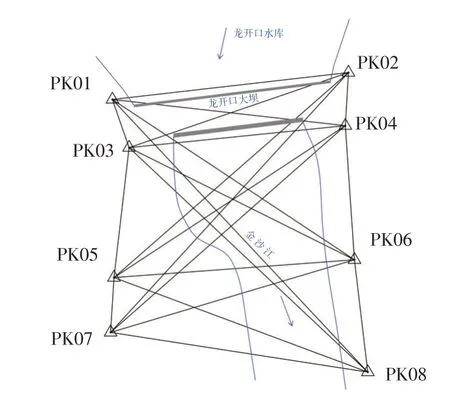
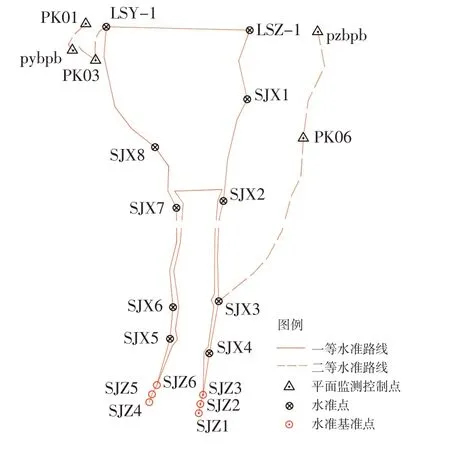
法方程的秩rk(A)=q,q 通常两期复测为同精度,但由于存在观测误差,两期单位权方差估值不相同。在应用平均间隙法前,需进行两期观测同精度检验。作原假设H0:两期观测同精度,构造一个服从F分布的统计量为两期单位权方差估值;检验量F=F(α,f1,f2),α为显著水平,f1、f2分别为两期观测多余观测总数。选定α,查F分布分位数表,当P≤F时,接受原假设,否则认为两期观测不同精度。两期观测精度不同,可用t 检验法,限于篇幅,此处不作展开。两期观测同精度则采用平均间隙法,分为整体检验和局部检验,流程见图1。 图1 平均间隙法稳定性分析流程图 根据两期复测数据,按自由网平差,得到两期观测值改正数(残差),再由改正数计算每期的单位权方差估值[10-11],则有: 式中,Pd为Qd的广义逆;fs为独立的间隙个数。 作原假设H0:两期观测期间所有监测网点都是稳定的,则间隙与观测值改正数均视为正态变量,为同一正态母体方差的无偏估值,构造服从F分布的统计量,其中α为显著水平,选定α,查F分布分位数表,若F≤F(α,fs,f),则接受原假设,即所有监测网点都是稳定的;否则表明网中存在不稳定点,需进一步通过局部检验,逐点分析找出所有不稳定点。 设检测网点存在稳定点组F和不稳定点组M,则间隙矩阵和协因数逆矩阵Pd分别为: 采用以下变换,则有: 首先以边长、高差同精度检测限差为准则,通过两期实际边长、高差比较,初步判断前期起算点的相对稳定性(小于限差的,判断为稳定);再对比本期平差坐标、高程与前期坐标、高程计算点位差ΔP、高差ΔH与点位中误差MP或高程中误差MH,若,则 为 稳定 点[12];剔除比值≥2 2 的点,再次拟稳平差,直至所有网点比值<2 2,剩余点即为拟稳点。 龙开口水电站位于金沙江中游,坝后式厂房布置在右岸台地上,总装机1 800 MW;2012年11月25日下闸蓄水,2013年5月首台机组发电,2014年1月第5台机组并网发电。为了对龙开口水电站大坝、左右岸边坡以及近坝区滑坡体外部进行日常变形监测,左右岸边坡、大坝坝顶和坝后表面设有若干个位移监测点。左右岸还设有平面变形监测自动化工作基点和后视点,采用极坐标法进行观测;大坝、左右岸边坡垂直位移采用水准测量。平面和高程的监测控制网是日常监测工作的基础,龙开口监测控制网于2012年进行了首期建网,坐标系统、高程基准与勘测设计、施工阶段一致;2013 年起逐年对监测控制网进行复测;2015 年对出现位移的PK01、PK07 两点进行重新选点埋设并重新建网。首期建网、各期复测网精度均达到一等监测控制网精度。一等平面位移监测基准网由PK01~PK08共8个钢筋混凝土观测墩组成,网形为边角网,边长数为22 条(图2)。左右岸边坡表面变形监测两个自动化工作基点、两个后视点与PK01~PK06组成工作基点网。一等垂直位移监测控制网由基准点SJZ1~SJZ6,间隙点SJX1~SJX8,工作基点LSdbz-1、LSdby-1,共16个网点组成,水准路线见图3。 图2 平面位移监测控制网布置图 图3 水准路线示意图 监测控制网的9 次复测均由业主单位分年度招标进行,2013—2015 年度、2016—2018 年度和2019—2021年度由不同中标单位实施。各年度监测控制网复测均采用全站仪、水准仪按照首期建网或上期复测方法,同精度观测。在外业观测数据检查无误、各项限差符合技术设计书要求后,采用间接平差法进行变形监测控制网严密平差计算,并进行粗差探测和分析。 2.2.1 平面位移监测网复测数据处理分析 2012 年首期建网时,以PK08 为固定点、以PK08—PK05 方向为固定方向进行经典平差,选取仪器标称精度作为先验中误差。2013—2015年度平面位移监测网复测,首先对固定点(起算点)PK08、起算方向点PK05进行稳定性分析,即对比PK08、PK05与其他各点边长与2012年的变化,结果表明各边变化量均在限差内,初步判定PK08、PK05 基本稳定。以PK08为起算点、以PK08—PK05方向为起算方位,起算数据沿用初期建网成果进行经典平差。以2012年首期建网成果为基准值,比较各年复测的平差成果,计算各期平面位移量;以设计要求的最弱点位中误差的两倍(±3.0 mm)为位移量限差,分析可知2015 年复测发现PK03坐标发生顺坡向库区方向显著位移,2013—2015年的位移量分别为1.0 mm、1.8 mm、3.8 mm,有一定的累积趋势,在后续观测中应加强关注,其余各点变量均在限差内,未见显著位移,建议使用复测成果。 2016—2018年度平面位移监测网复测,首先根据各监测网点所在位置的地质构造,初步判定PK08、PK05 稳定性较好;然后进行两期观测同精度检验,若精度相同,则采用平均间隙法进行监测网点稳定性分析,若不同,则采用t检验法;最后以稳健迭代权法进行监测网点稳定性分析,结果与平均间隙法或t检验法基本一致。复测稳定性分析表明,PK08 相对稳定,以PK08 为起算点、以PK08—PK05 方向为起算方位,沿用上一次复测起算数据进行经典平差并提交平差成果,统计各次复测累积平面位移量并形成图表。 2019—2021年度平面位移监测网复测,首先初步判定PK08、PK05 基本稳定,采用一点一方向经典平差,确认复测网平差后各项指标达到一等边角网精度要求;再以前次平差结果为近似值,结合本次观测数据进行有特类值的拟稳平差,得到各点本次平差坐标与点位中误差;然后根据本次坐标与前次坐标计算两次点位差与本次点位中误差的比值ΔP ∕MP,若比值<2 2,则认为该点稳定,否则为动点,剔除动点再次拟稳平差,分析并剔除动点,重复拟稳平差,直至剩余点均满足比值<2 2,平差结束,将最终拟稳平差结果作为提交成果。由此可知,采用不同的拟稳点进行多次拟稳平差,方向观测值、距离观测值个数相同,平差的相对图形不变;但点位中误差、平差结果有所不同。2021年复测首次拟稳平差将所有网点作为拟稳点,第二次拟稳平差剔除不稳定点PK06,第三次拟稳平差剔除不稳定点PK02,说明选取合理的拟稳点进行拟稳平差,才能获取复测基准网点真实可靠的现势性平面数据。 2.2.2 垂直位移监测网复测数据处理分析 2013—2015年度垂直位移监测网复测,首先检查位于大坝下游的基准点组SJZ1~SJZ3、SJZ4~SJZ6点间高差,判断基准点组稳定性较好;再以左岸基准点SJZ1和右岸基准点SJZ6为高程控制网起算点,起算数据沿用初期建网成果,进行附合网平差;然后以2012年首期建网成果为基准值,比较各年复测的平差成果,计算各期垂直位移量;最后以设计要求的最弱点高程中误差的两倍(±3.0 mm)为高程变化限差,分析可知基准点未出现明显沉降,而两个工作基点LSY-1、LSZ-1和间隙点SJX4~SJX8均出现了明显沉降,建议以复测成果为准。2016—2018年度垂直位移监测网复测,首先采用平均间隙法和稳健迭代权法检验所有垂直位移监测网点的稳定性,两种方法检验结果基本一致,基准点SJZ1~SJZ3 是稳定的;再以SJZ1 为起算点,沿用上一次复测起算数据进行经典平差,提交平差成果;最后统计各次复测累积垂直位移量并形成图表。2019—2021年度垂直位移监测网复测,首先检查位于大坝下游的基准点组SJZ1~SJZ3、SJZ4~SJZ6点间高差,远小于规范限差,判断基准点组稳定性较好;再以左岸基准点SJZ1为高程控制网起算点,起算数据沿用初期建网成果,进行经典平差;然后与上期成果进行比较,计算两期垂直位移量ΔH,若大于倍高程中误差MH,则为不稳定点;最后逐一剔除不稳定点,进行拟稳平差并提交成果。 上述工程实例验证了变形监测网拟稳平差的适用性和优越性,其关键是拟稳点的分析和选取。常用方法各具特点,通过实践分析讨论后得出以下结论: 1)平均间隙法是应用统计检验理论分析基准点稳定性的有效方法。在实际应用中,有的测量工作者将整体检验称为平均间隙法,将局部检验称为分块检验法或单点检验法,本是一个完整的假设检验被理解成两种方法,是不合理的。 2)平均间隙法计算量大,有多次矩阵运算,特别是局部检验时,迭代次数多,解算效率偏低。若采用具有自动搜索算法的软件,该问题能够得以解决[13]。 3)限差法数学模型容易构造、使用简便,但判定准则类似经验公式,有待于结合实际工作进一步研究或与其他方法结合使用。 4)利用监测网点所在的地质构造条件分析其稳定性,属模糊聚类技术,更适合区域地壳变形监测网的拟稳点选取,因为其需要大量地质、水文和气象等基础资料支撑;稳健迭代权法虽然严谨可靠,但需进行大量迭代计算,基准转换复杂,解算效率较低,需要成熟的编程软件。 5)拟稳点选取得当,以拟稳平差结果为使用成果,能提高监测网灵敏度;通过数据挖掘(作差、作比计算)生成各期间和累计位移量图、表,数据可比性强。 拟稳平差的合理性是基于多余观测和控制网中部分点稳定的,工程变形监测网宜先用限差法,再用平均间隙法进行拟稳点分析,互相验证,确保拟稳点选取正确。需要强调的是,经过分析若控制网中少于两个稳定点,则无法采用拟稳平差方法。1.2 平均间隙法
1.3 限差法
2 工程监测网实例
2.1 龙开口水电站变形监测网概况
2.2 监测控制网复测实施
3 结语
