基于机器学习的盾构掘进地表沉降回归预测模型
2023-10-11方诗圣苏一恒林彤彤修贤好李建豪
方诗圣, 苏一恒, 林彤彤, 修贤好, 李建豪
(1.合肥工业大学 土木与水利工程学院,安徽 宣城 242000; 2.合肥工业大学 计算机与信息学院,安徽 宣城 242000)
城市地铁盾构工程施工引起地表沉降与塌陷问题因其对城市建筑物及道路的危害性受到工程界广泛的关注,大量学者正在进行相关研究[1-2]。现有的地表沉降预测方法可分为经验和半经验公式[3-4]、解析法[5]、数值模拟[6]、模型试验[7]、机器学习算法预测[8]。
Peck公式是最早建立在隧道掘进地表沉降变形观测数据上的经验公式。文献[3]研究了基于Peck公式的双线盾构引起的土体沉降前后期结算叠加的三维计算公式;文献[4]研究了利用合肥轨道交通盾构施工中的地表监测数据对Peck公式进行验证,预测值与真实值平均误差为8%。解析法在假设条件下建立力场求解。经验法简单易行准确性较差,解析法精度较高但依赖于特定条件,两者不适应于复杂工程地形。数值模拟通过ANSYS、ABAQUS、FLAC3D等数值模拟软件综合考虑施工条件和土体参数,模拟隧道开挖过程。但前期准备工作复杂且预测结果受模型划分等因素影响较大。模型试验通过几何比例物理条件相似的装置简化研究地表沉降,不适用于工程生产。
作为近年新兴的一类方法,机器学习是使用统计技术从观察到的数据中构建模型的方法。针对传统预测方法精度不高或求解困难的问题,本文基于多种机器学习算法的拟合能力,提出盾构掘进沿线地表最大沉降值预测模型并评价出最优算法。
1 沉降预测方法
1.1 模型框架
本文采用机器学习算法搭建模型,用于预测盾构掘进引起的环线中心线位置地面纵向沉降稳定值,盾构掘进沉降示意图如图1所示。
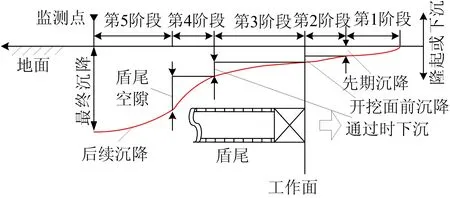
图1 盾构掘进沉降示意图
用于盾构掘进过程中的沉降预测模型框架可分为3个阶段,如图2所示。

图2 沉降预测模型框架图
1) 数据收集阶段。监测地表沉降并绘制地面沉降图,获得地表最大沉降值。根据需要并结合实际选取3类特征参数(可控不可预测类、不可控可预测类、不可控不可预测类)作为数据集中的输入参数。
2) 学习阶段。将数据进行预处理,筛去异常的数据,保留合理的数据。输入至回归预测模型中,调整超参数进行训练。对预测值采用均方误差(mean square error,MSE)、均方根误差(root mean square error,RMSE)、绝对均值误差(mean absolute error,MAE)和决定系数R24种评估指标进行评价,选取性能最好的模型用于实际预测。
3) 预测阶段。将之前已经选好的数据集中的输入参数代入学习阶段中性能最好的回归预测模型中,即可得出地表最大沉降预测值。将输出值与实际值进行对比,分析其可靠程度。
1.2 模型算法
机器学习中与回归有关的模型众多,理论上可以用回归方法分析地表隧道中心线位置的沉降值与影响因素之间的关系。本文中用到的回归模型主要有线性模型、树模型、支持向量机(support vector machine,SVM)、多层感知机(multi-layer perceptron,MLP)。
1.2.1 线性模型
多元线性回归分析是最基础的回归分析方法,其回归模型如下:
(1)

线性回归模型的损失函数选择MSE,计算公式为:
(2)
其中:m为样本数量;wi为模型的系数;xi为样本自变量;yi为对应的实际观测值。
岭回归是一种改良的最小二乘估计法,通过对系数的大小施加惩罚来解决普通线性回归的一些问题。
(3)
套索算法(least absolute shrinkage and selection operator,LASSO)是另一个正则化的线性模型,可以降低给定解对特征数的依赖程度。它的损失函数在式(2)添加正则化项,即
(4)
1.2.2 树模型
分裂决策树(classification and regression tree,CART)[9]构建二叉决策树,递归生成CART回归树,并通过控制树的深度来停止分支节点的分裂。
本文中用到的是随机森林的回归模型,使用了CART回归树作为弱学习器。使用随机森林进行地表中心线最大沉降值预测的过程如下:首先在训练数据集中Bootsrap抽样(随机且有放回抽取),构成n个不同的子样本;然后在每个样本生成1棵CART回归树;最后,通过对构建的若干个不同的CART回归树预测结果取平均获得最终沉降预测值如图3所示。

图3 随机森林预测过程
XGBoost(extreme gradient boosting)是一个优化的分布式梯度提升库,可以快速准确地解决许多数据科学问题,属于树模型一类。
1.2.3 支持向量机
SVM是用于分类、回归和异常检测的监督学习方法。本文对数据进行标准化处理使得经过处理的数据符合标准正态分布。
本文采用支持向量回归(support vector regression,SVR)和LinearSVR 2种支持向量回归方法进行实验。LinearSVR提供了比SVR更快的实现,但只考虑了线性内核,不适用于非线性问题。SVR默认使用径向基函数。在使用径向基函数训练支持向量机的过程中,重点考虑正则化系数c和核参数gamma 2个超参数。
1.2.4 多层感知机
MLP是一种人工神经网络。在本文中,影响地表中心线最大沉降值的参数信息通过MLP的输入节点流入,中间经过2个隐藏层,神经元个数分别为20、10,最后经过包含1个神经元的输出层,输出地表中心线最大沉降预测值。其中,隐藏层采用ReLU(rectified linear unit)激活函数,实现神经网络层之间的非线性变换,从而提升模型的表达能力。
1.3 评价指标
在模型训练中,最终要达成的目的是得到准确的预测,因此寻找真实值与预测值的差异是对算法模型评估的关键所在。评价预测的效果通常需要考虑预测的数值是否正确、拟合程度是否满意。本文选取以下4种评估指标。
1) MSE的计算公式为:
(5)
MSE首先计算每个样本的预测值与真实值差值的平方,然后求和再取平均值。MSE的值越小,预测模型描述实验数据的精确度越高。
2) RMSE的计算公式为:
(6)
RMSE也被称为标准误差,它是MSE的二次方根。因为RMSE与数据为相同量级,所以RMSE能更好地描述数据。与相当于L1范数的MAE相比,相当于L2范数的RMSE对异常值更敏感。
3) MAE的计算公式为:
(7)
MAE为预测值与真实值的误差绝对值的均值,能更好地反映预测值误差的实际情况,其值越小说明拟合效果越好。
4) 决定系数R2。计算公式为:
(8)
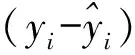
2 数据库的建立
2.1 数据源
数据来源于安徽省合肥市轨道交通8号线北城世纪城站至泉河路站区间,位置里程为DK40+670787—DK 42+554836。线路呈V字形坡,最大坡度为25%,线间距13~15 m,埋深9.52~28.07 m;区间隧道管片内径55 m,外径62 m,每环管片宽15 m,平面曲线半径R≤400 m,曲线段环宽12 m。所在地貌为二级阶地,岩土层可划分为3个单元层和7个亚层。监测仪器采用TrimbleDINI03,监测点布置为沿线路中心线纵向每10~30 m设置1个测点;盾构始发、接收段附近100 m范围内,每20 m设1个断面;其余地段,每50 m设1个断面。
2.2 输入参数
在使用机器学习算法进行隧道沉降预测时,必须要选取合适的参数进行分析,包括可控不可预测、不可控可预测、不可控不可预测3类。
对于可控不可预测类因素包括所有的盾构施工参数。参数选取示意图如图4所示,在盾构施工参数中,推力、扭矩、贯入度与土仓压力是盾构掘进过程中与地层扰动有关的参数,而且它们不但是盾构掘进控制的重要参数,还可以实时获取、准确可靠。根据文献[10]的研究,注浆量对盾构空隙以及后期的沉降有较大的影响,因此选取这5个参数作为输入参数。

图4 参数选取示意图
对于不可控可预测类因素包括地质条件、操作失误、盾构机缺陷等,在此本文仅考虑地质条件。考虑到地质条件的复杂性与隐蔽性,本文仅选取几个影响较大的因素作为参数。文献[11]在研究中综合地考虑了岩土层的物理力学性质与空间位置信息,选择修正标贯次数、修正动探次数、修正单轴抗压强度这3个参数作为输入参数。文献[12]研究表明,土体中孔隙水压力在相对压强小于0的范围内降低时,将引起土体等向压缩,在相对压强大于0的范围内降低时,将引起土体单向压缩,造成沉降。而地下水渗漏会导致孔隙水压力降低,因此地下水的深度也作为输入参数。
对于不可控不可预测类因素包括盾构类型、盾构埋深与直径之比、灾难性地质条件3个因素。对于同一隧道工程,盾构类型未改变,灾害性地质条件难以确定。因此仅考虑盾构埋深与直径之比作为输入的初始参数。初始参数如下:盾构总推力为6×104kN;刀盘扭矩为3 100 kN·m;贯入度为36 mm; 实际土压力为0.05 MPa; 实际注浆量为5 m3;修正标贯次数为8.29;修正动探次数为1;修正单轴抗压强度为50.8 MPa; 地下水的深度为47.109 m; 盾构埋深与直径之比为1.557;监测沉降值为-1.12 mm。3类影响参数共计1项内容作为初始参数用于沉降预测模型的训练。
3 预测结果
3.1 超参数确定
超参数优化先确定搜索的参数空间,然后进行抽样和实验,采用交叉验证的方案来获得最佳交叉验证分数,从而获得最佳参数。比如岭回归的超参数α,SVR的核参数gamma、正则化系统c,随机森林的超参数max-features、n-estimators等等。
岭回归的超参数α表示模型正则化的强度。在模型中,执行留一法交叉验证,衡量指标默认为MSE,α的取值区间设置为[0.001,1.001],步长为0.02。岭回归超参数α与损失值变化如图5所示,当α=0.75时,损失达到最小值。

图5 岭回归超参数α与损失值变化
SVR有正则化系数c和核参数gamma 2个重要的超参数在模型中,SVR的核函数为径向基函数gamma参数控制单个训练点的影响距离。尝试的分布为“c”:uniform(1,10),“gamma”:reciprocal(0.001,0.100)。采样的参数设置数量n-iters为10,采取随机参数优化的方式和三折交叉验证,以R2为衡量指标,最终确定超参数c为7.011,gamma为0.026 1。
随机森林调整的超参数为max-features、n-estimators,max-features为寻找最佳分割时要考虑的特征数量,n-estimators为构成森林的树的数量。本文使用网格搜索(GridSearchCV)进行参数估计。指定搜索“n-estimators”:[3,10,30],“max-features”:[2,3,4]2个网格,总共有9种组合。同样地,采用三折交叉验证,以R2为衡量指标。当“max-features”: 4,“n-estimators”:30时,交叉验证的评分最高。
3.2 沉降预测结果
沉降监测值来源于实地电子激光测距仪监测。监测值为盾构掘进到预设监测断面10 d内环线中心处最大沉降值。共收集到358组数据。通过噪声去除,保留270环真实可靠数据。
从中随机选取20%共54组的数据作为测试集,进行沉降结果的预测。通过训练集和超参数确定完善各预测模型。将测试集输入各预测模型,得到盾构沉降预测值与监测值的结果,见表1所列。
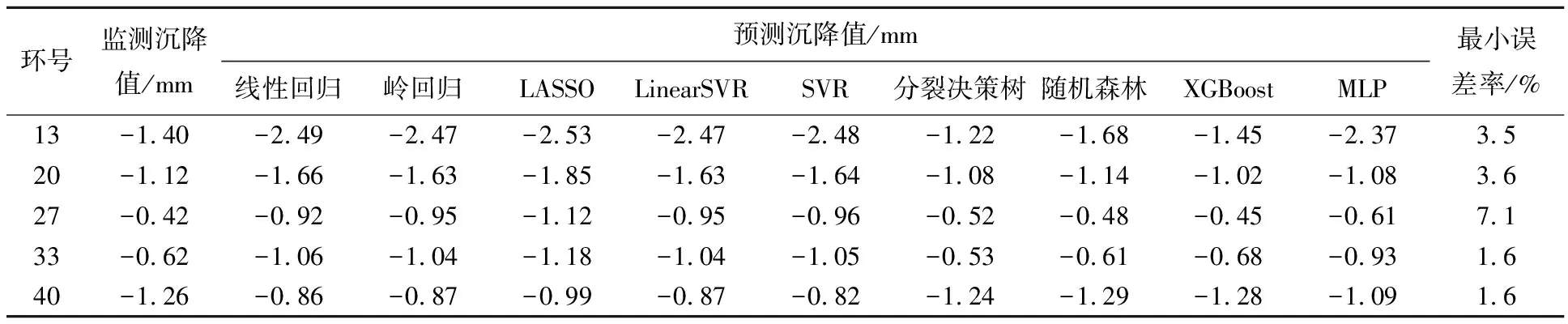
表1 盾构沉降预测值与监测值
总体来看,各个模型总体预测值在距离较小时与实际值较为符合,其中平均误差为4%,但部分模型预测的最终沉降值与实际值相差较大,因此需进一步对比分析找出最优算法。
3.3 算法性能比较
为进一步比较各模型预测效果,采用4个评价指标比较各算法性能。总体上,神经网络模型和树模型拟合效果优于线性模型。
对3个线性模型性能单独分析。线性模型算法性能评价结果如图6所示。
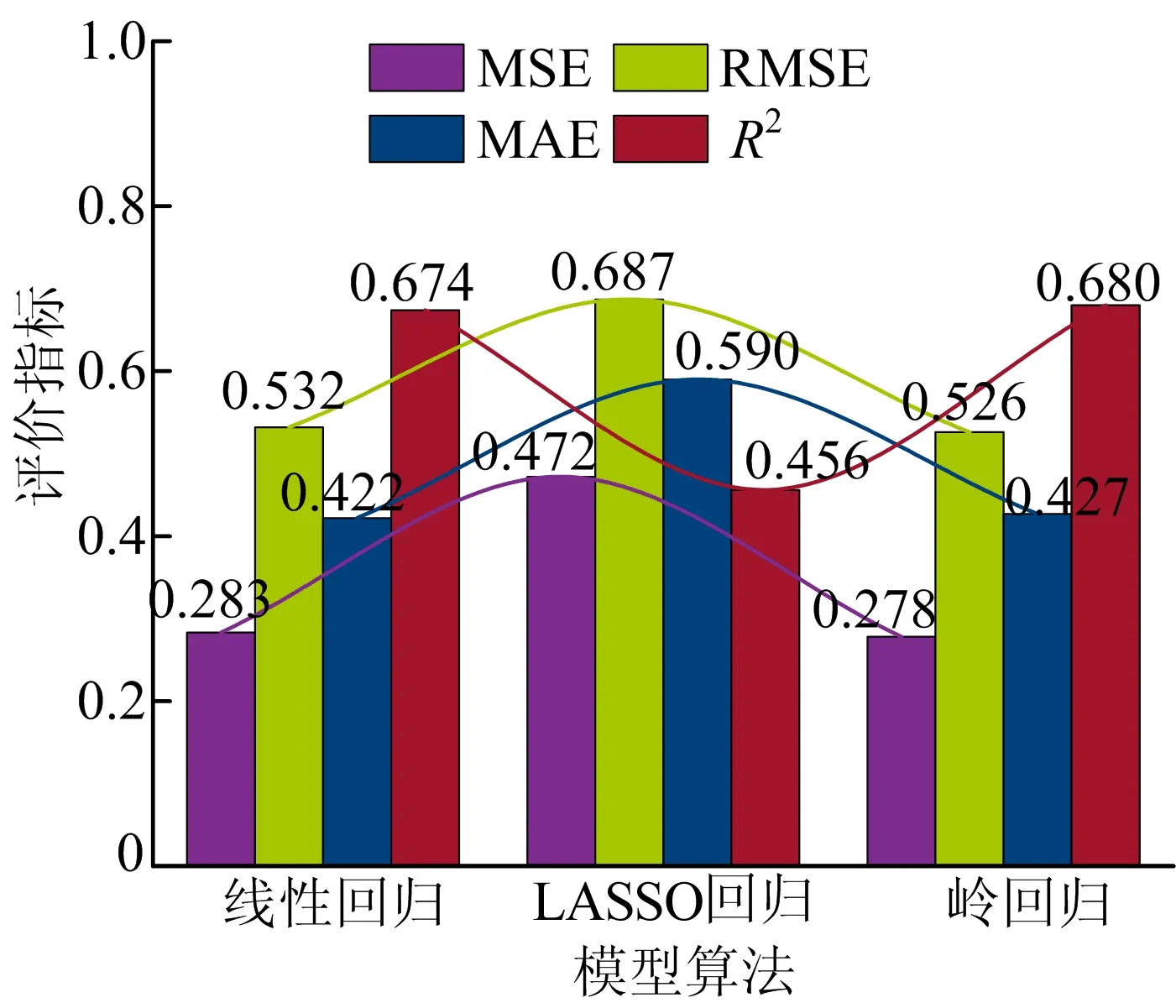
图6 线性模型算法性能评价结果
从图6可以看出,岭回归与线性回归的各个值都相差不大,岭回归的效果会略好于线性回归。而LASSO回归的R2较小,MSE、RMSE和MAE相对于其他2个线性模型都偏大,效果最不理想。在对3个线性模型分析结果可知,岭回归的效果最好,是线性模型中的最优解。
对树模型进行分析,将随机森林与决策树模型的各个数值对比。树模型算法性能评价结果如图7所示。
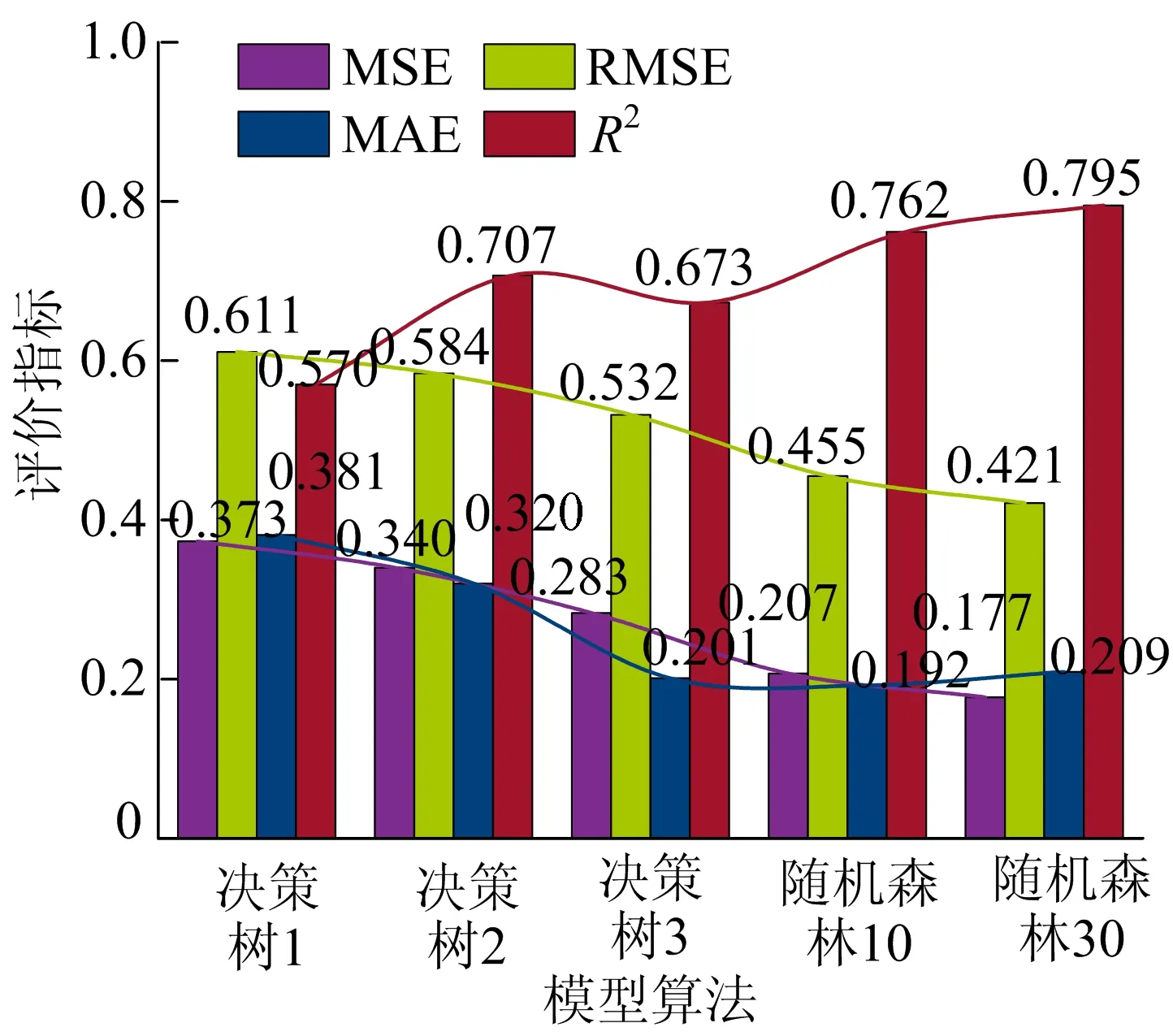
图7 树模型算法性能评价结果
图7中:决策树1~决策树3的深度为1~3;随机森林10、随机森林30的子样本为10、30。从图7可以看出,随机森林的R2明显高于决策树,且随机森林的MSE、RMSE和MAE误差整体都要低于决策树模型,表现更为稳定。在2种树模型中,随机森林的表现效果较优,可以优先选用。
SVR作为SVM的重要分支,其R2显著高于SVM,且其MSE、RMS和MAE整体都要低于SVM,综合来看SVR的表现性能要明显好于SVM的。而MLP的各个数值都与SVR相接近,在所有模型中表现性能仅次于SVR。
XGBoost与神经网络算法评价结果如图8所示。对于XGBoost与神经网络算法,可以优先选用SVR作为首选算法,MLP可以作为备选算法来考虑。

图8 XGBoost与神经网络算法评价结果
4 结 论
本文提出了基于多种机器学习算法的盾构掘进沿线地表最大沉降值预测模型,最终通过合肥地铁轨道8号线实测工程数据进行评价分析确定了最优算法。
结果表明:总体上神经网络模型和树模型拟合效果优于线性模型;树模型中随机森林与决策树模型相差微小,随机森林表现更为稳定;对于XGBoost与神经网络算法,SVR的R2显著高于其余算法,达到0.865,且其MSE、RMSE和MAE整体较低且较稳定,效果最理想。
在处理盾构沉降预测问题上,SVR算法模型存在对异常值不敏感,泛化能力强,具有较好的鲁棒性等优点。其预测值与真实值平均误差率为3.19%,精度较高。
因为本文的数据库建立于合肥地铁轨道8号线工程,所以不同地区的土层性能差距较大等客观因素可能导致沉降值预测模型的结果出现波动。
