Improved quantum(t,n)threshold group signature

Yaodong Zhang(张耀东), Feng Liu(刘锋), and Haixin Zuo(左海新)

1College of Computer Science and Technology,Shandong Technology and Business University,Yantai 264005,China

2College of Mathematic and Information Science,Shandong Technology and Business University,Yantai 264005,China

Keywords: quantum(t,n)threshold signature, quantum(t,n)threshold secret sharing, forgery attack, collusion attack

1.Introduction

As an important branch of the digital signature scheme,threshold signature can ensure the security of transmitted information,provide data integrity and realize identity authentication.After Desmedt and Frankel[1]first proposed the(t,n)threshold signature scheme in 1991,the study of threshold signature has become increasingly popular.For a threshold signature group consisting ofnmembers,a combination of greater than or equal totmembers can represent the group to sign messages.[2–4]

With the introduction of the Shor[5]algorithm, the security of traditional digital signatures has been greatly threatened.Cryptosystems based on quantum mechanics can achieve unconditional security,so the study of quantum signatures has become the focus of most researchers.The concept of a quantum signature was first introduced by Gottesman and Chuang[6]in 2001,but the public key in their scheme can only be used once.To make quantum signatures more practical,the first arbitrated quantum signature based on Greenberger–Horne–Zeilinger states was proposed by Zenget al.[7]in 2002.Subsequently,arbitrated quantum signatures gradually became the basic quantum signature scheme.[8–12]Although quantum signature schemes are emerging,many are still in the theoretical research stage.In recent years,many physically realizable quantum signature schemes have been proposed,[13–17]for example Yinet al.[13]produced the first work on practical quantum digital signature without secure channels and performed the first experiment without assuming any secure channel,[14]while Luet al.[15]solved two major restrictions of quantum signatures by a post-matching method.These studies paved the way for the practical application of quantum signatures.The present paper concerns a quantum (t,n) threshold signature scheme based ond-dimensional quantum systems; it is still in the theoretical research stage and its physical implementation needs further study.

For a threshold signature, the requirement of a threshold is essential.We added the quantum threshold secret sharing technique to the original signature scheme as part of the design of this new scheme.In 2017,Songet al.[18]implemented classical secret sharing based on Shamir secret sharing and the quantum Fourier transform technique.However,their scheme was later shown to be incapable of recovering the secret.In 2018, Mashhadi[19]designed a hybrid secret sharing scheme based on quantum Fourier transform and a monotonic spanning program that implements the features of classical and quantum secret sharing.In 2021,Sutradharet al.[20]improved the scheme of Songet al.by increasing the number of quantum Fourier inversions,making the scheme more complex.In this paper we design a threshold scheme based on Shamir secret sharing and the quantum Fourier transform that can be added to quantum signatures.Compared with the previous secret sharing schemes, our scheme does not contain quantum Fourier inversions and significantly reduces the number of quantum measurements.

Recently, a quantum (t,n) threshold group signature scheme that uses techniques such as quantum-controlled-not operations and quantum teleportation was analyzed.[21]After analysis of the scheme by Guoet al.,[22]the original scheme was found not to be a(t,n)threshold group signature scheme because any number of members in the scheme could generate a valid signature.The original scheme also has problems with key leakage and trustworthiness of the arbitrator.After our analysis of Qinet al.’s scheme,[21]we also found that a forgery attack cannot be resisted in the original scheme.

To address the above issues, we applied the designed quantum (t,n) threshold secret sharing technique to the original signature scheme[21]and improved the original signature scheme.The analysis shows that the improved scheme can resist forgery attack and collusion attack, and it is undeniable.At the same time,this scheme reduces the level of trust in the arbitrator during the signature phase.

2.Preliminaries

In this section we define the preliminaries of our scheme,including Shamir secret sharing, quantum Fourier transform(QFT),the SUM gate and the generalized Pauli operator.

(i)Shamir secret sharing:[23]Share generation:the dealer uses at-1 order polynomial to assignnsecret shares tonsigning participants

Secret reconstruction: greater than or equal to the threshold number of participants reconstruct the secret

(ii)Quantum Fourier transform:[24,25]The QFT is a quantum version of the standard discrete Fourier transform,which is a unitary transformation of a quantum system.Forα,β ∈{0,1,...,d-1},the QFT is defined as

(iii)The SUM gate:[26,27]Ind-dimensional Hilbert space,the quantum SUM gate is defined by

where|x〉 is the control particle,|y〉 is the target particle andx,y ∈{0,1,...,d-1}.

(iv)Ind-dimensional Hilbert space,the generalized Pauli operator is defined by[28,29]

whereα,β ∈{0,1,...,d-1},ω= e2πi/dand+denotes the addition moduled.In particular,whenα,β ∈{0,1},we have

3.Brief review of Qin’s scheme

In this section, we briefly introduce the quantum (t,n)threshold group signature scheme proposed by Qinet al.in 2020,[21]as well as pointing out the security problems in the scheme.

3.1.Initializing phase

The quantum message being signed hasmquantum states.Alicei(i ∈{1,2,...,n})and Charlie share the private keyKAivia the quantum key distribution (QKD) protocol, Bob and Charlie share the private keyKB, both in 2mbits.Aliceiand Bob sharemBell states, Aliceiholds the particle|aij〉, Bob holds the particle|bij〉.

3.2.Signing phase

3.3.Verifying phase

(v) Bob compares whether|P3〉 is equal to|P2〉.If they are equal,Bob accepts the signature;otherwise,he rejects it.

4.Security issues in the original scheme

Guoet al.[22]pointed out that the quantum (t,n) threshold group signature scheme proposed by Qinet al.[21]has the following three issues:

(i) The original scheme is not the (t,n) threshold group signature scheme.The signature process of the scheme does not conform to the meaning of threshold signature: a valid signature can be generated only whentor more members sign together,otherwise a valid signature cannot be generated.

(ii)Bob can get both the encrypted classical messageCi′and the corresponding textCi.Then applying the XOR operation on these two messages bit by bit, Bob can learn the keyKAi.Namely Bob can fabricate a valid signature for any message.

(iii) The arbitrator Charlie is completely trusted, which can cause greater difficulties in the practical application.

Through our analysis of Qinet al.’s scheme, we found that the scheme has another security issue.This issue will enable Bob to forge the signature and makes Charlie lose the right to arbitrate the signature.The analysis is as follows:

HereEKiA∈{X,Z}are the Pauli operators.From the commutativity of Pauli operators

Bob can perform the same Pauli operationUion|R〉and|P2〉

whereUi ∈{I,X,Z,iY}.Since the global phase factor±1 has no observed effect under the quantum swap test circuit of quantum states, (|P*〉,|R*〉) can always pass Charlie’s verification.After(|P*〉,|R*〉)has passed Charlie’s verification,the signatureS*=E(Ci,|R*〉)will be generated.Thus Bob completes the forgery of the signature.Later, if there is a dispute over the signature,Alice claims that she did not sign the message|P*〉and the arbitrator Charlie will check|P*〉and|R*〉.After checking, Charlie will think Alice is lying.So Charlie makes an error of judgment and loses his arbitration.

5.Improved scheme

The members of our scheme includenmembers of signature groupN={Alice1,Alice2,...,Alicen}, the signature receiver Bob and the arbitrator Charlie.The improved scheme consists of three parts: the initialization phase, the signature phase and the verification phase.

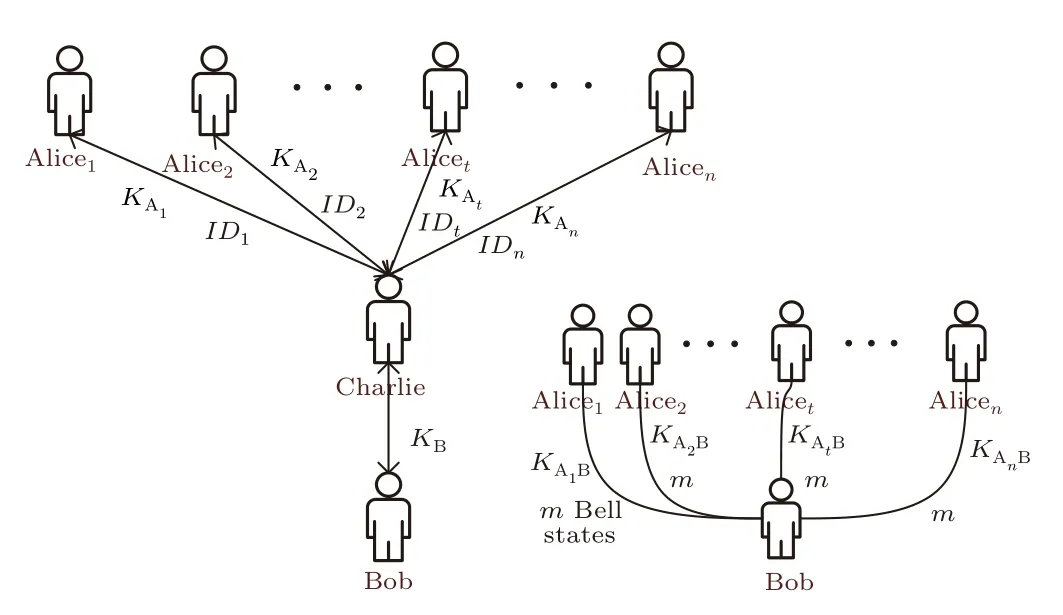
Fig.1.The initialization phase of the proposed scheme.

5.1.Initialization phase

(i) Each of{Alice1,Alice2,...,Alicen}shares a private keyKAiwith Charlie,Bob shares a private keyKBwith Charlie and each of{Alice1,Alice2,...,Alicen}shares a private keyKAiBwith Bob.All keys are 2mbits.All the above processes are implemented by quantum key distribution or quantum secure direct communication.[31–33]

(iv) There is a correspondence between any single bitiand qubit|i〉in the scheme as follows:

Its measurement form is known to all participants.In addition,the Bell pair in the scheme has the following correspondence with the two classical bits:

5.2.Signature phase

(i)Without loss of generality,let

whereτi=(l1+l2+···+lm)modmandSmis equivalent to a circular shift operation onmqubits.Alice1encrypts|P1〉first,and the rest of Alicerencrypts it in turn.The encryption form is

{Alice1,Alice2,...,Alicet}preparemdecoy photons, each chosen randomly from the set{|r〉}and{QFT|r〉},r ∈{0,1,...,d-1},and insert themdecoy photons randomly into|RA〉.

where+denotes addition modulod.The state|φ2〉evolves as state|φ3〉:

Aliceiuses the computational basis{|0〉,|1〉,...,|d-1〉}to measure|Ki+Si〉,then Aliceiobtains and saves the measurement result (Ki+Si).(Ki+Si) is converted to a binary bit string and converted to|KSi〉according to Eq.(8).

For example,taket=3,n=5,d=7,K1=5 andS1=6.ThenK1+S1=4 mod 7,4(10)→0100(2).

Fig.2.The flow-process diagram of the proposed scheme.

5.3.Verification phase

(i) Bob directly encrypts the information sent from{Alice1,Alice2,...,Alicet}with the private keyKBand sends it to Charlie.

(ii) Charlie uses his private keyKBto decrypt the information from Bob and gets|RA〉,|KSi〉,|P2〉,EKAiB|Ci〉.{Alice1,Alice2,...,Alicet}tell Charlie the location of the decoy photons and the preparation basis.Charlie uses the preparation basis to measure the decoy photons at the corresponding positions and tells{Alice1,Alice2,...,Alicet}the measurement results, and{Alice1,Alice2,...,Alicet}determines whether the decoy photons are eavesdropped by comparing the initial states of the decoy photons.If the quantum channel is insecure,then the protocol is terminated;otherwise,the protocol is continued.

6.Analysis of improvement scheme

In this section,we will prove the correctness and security of the improved scheme and compare the performance of our improved scheme with the original scheme.

6.1.Correctness

For the correctness of the scheme, we focus on the correctness of the(t,n)threshold and the correctness of the verification phase.

6.1.1.Correctness of the (t,n) threshold

In the signature phase,Alice1gets|φ1〉by performing the QFT on the first particle|0〉1.Then, Alice1performs SUM operation on|0〉rand gets|φ2〉:

Alicei(i ∈{1,2,···,t})performs QFT andUSi,0on her particle,and gets|φ3〉:

and we have

Similarly

Therefore,

By the Lagrange interpolation formula

6.1.2.Correctness of the verification phase

Table 1. m(t-1)CNOT operations.

After all Alicej’s measurements are completed, Bob performs corresponding unitary operations on|bij〉 according to the measurement results.Then Bob obtains (α1|00···0〉+β1|11···1〉)⊗···⊗(αm|00···0〉+βm|11···1〉).Bob measures the firstt-1 qubits in the basis{|+〉,|-〉}.For example

can be expressed as

6.2.Security

The security characteristics of the quantum(t,n)threshold group signature scheme are mainly unforgeability, nonrepudiation and resistance of collusion attack.

6.2.1.Unforgeability

In their analysis Qinet al.[21]used the QOTP algorithm for encryption many times in their scheme,so that Bob can getCiandCi′at the same time.Bob can get the private keyKAiby the XOR operation,which leads Bob to forge the message and signature.

In this paper, the encryption algorithm used is the keycontrolled-‘T’QOTP encryption algorithm.In the design of the scheme, we circumvent the problem that Bob can obtain both|Ci〉and its ciphertext.We encrypt|Ci〉using the private keyKAiB,and we insert decoy photons into the sent quantum sequence.In this way,we guarantee both that Bob will not recover Alicei’s private keyKAiand that|Ci〉will not be falsified by the malicious arbitrator Charlie.

6.2.2.Non-repudiation

A valid signature must be encrypted by the signer’s private key.In this paper’s scheme,|RA〉,|KSi〉 and|Ci〉 are all encrypted by Alicei’s private key(i ∈{1,2,...,t}),so Charlie and Bob can determine whether the signature comes from a member of the signature group and Aliceicannot deny it.In the signature verification phase,Charlie first checks the legitimacy of the signature and then sends it to Bob to verify its correctness.Therefore, Bob cannot reject a valid and legitimate signature.

6.2.3.Resistance to known signature attack

In the scheme of this paper, Bob receives the|RA〉 and the message|P2〉from{Alice1,Alice2,...,Alicet}.For the encryption of|RA〉we use the‘T’QOTP encryption algorithm of Zhanget al.[35]If Bob performs the unitary operations on|RA〉and|P2〉:

Zhanget al.[35]point out that no one can conclusively determine the form of the cryptographic operator other than the legitimate participants in‘T’QOTP to achieve the correct unitary operation for each qubit,since the controlled transposition operationSmacts on allmqubits.That iswhereuiis a unitary operation on one qubit.They also point out that the probability of this encryption algorithm being successfully forged is (1/m)n, withnbeing the number of qubits forged by Bob.In addition to this, we also inserted random decoy photons in the ciphertext|RA〉.Bob’s execution of the above attack method will inevitably change the state of the decoy photons to such an extent that they will be detected in subsequent eavesdropping detection; the signature process is thus aborted.

6.2.4.Resistance to collusion attack

For threshold signature schemes, collusion attack is one of the most representative types of attack.Here we demonstrate the security of our scheme using two types of collusion attack.

(i) Collusion attack fromt-1 members of signature group.

In this scheme, the secret share ofSiin the threshold phase requires Alicei’s private key for encryption.BecauseKAiis shared between Aliceiand Charlie via QKD, which is proven to be unconditionally secure[36],the other group members cannot obtain Alicei’s keyKAi.If an attacker wants to forge Alicei’s key, the probability of a successful forgery is(1/2)2m.When 2mis large enough, the probability of successful forgery is nearly 0.

(ii)Collusion attack fromt-1 members of the signature group and the malicious arbitrator Charlie.

Suppose a malicious arbitrator Charlie conspires witht-1 members of the signature group to attack.Thet-1 members of the signature group can easily obtain Alicei’s private keyKAi,and can thus easily forge|RA〉′and|KSi〉′.But in this scheme,|Ci〉is encrypted using the private keyKAiB,and even the arbitrator Charlie cannot know Alicei’s private keyKAiB.So the malicioust-1 members and arbitrator Charlie cannot forge a legitimate signature either.

6.3.Trustworthiness of the arbitrator

In the analysis above, the participation of the arbitrator Charlie in the collusion attack could not lead to forgery of a legitimate signature.We next analyze the trustworthiness of the arbitrator in terms of several other steps.

In summary, all malicious behaviors of arbitrator Charlie in our improved scheme can be checked, so the arbitrator Charlie in our scheme cannot be completely trusted.

6.4.Performance comparison

In this section, we analyze the performance of the improved quantum (t,n) threshold signature scheme.It mainly includes whether the scheme has the function of the (t,n)threshold,the class of the(t,n)threshold,whether the scheme is resistant to forgery attacks and the trustworthiness of arbitrator.

Table 2.Performance comparison of schemes.

In addition,we also compare the quantum(t,n)threshold part of our scheme with the existing (t,n) threshold scheme based on quantum Fourier transform.[18–20]In the scheme proposed by Songet al.,[18]the dealer uses polynomials to distribute classical secret shares and the secret reconstructors can perform CNOT operation and QFT-1operation to recover the secret, but they need to obtain information from other participants.The scheme of Mashhadi[19]uses MSP instead of polynomials,and the reconstructor generates entangled states through SUM operation and QFT, and then recovers secrets through QFT and the generalized Pauli operator.The scheme proposed by Sutardhar[20]is an improvement of Songet al.’s scheme, and requires each participant to perform the QFT-1operation on his own particle during the secret recovery phase.

In our scheme,we construct the quantum(t,n)threshold function in the original scheme using the Lagrange polynomial and quantum Fourier transform.Ourd-level(t,n)threshold is more difficult and practical than the 2-level (t,n) threshold.Our scheme does not need the QFT-1operation in the secret recovery phase,but only needs to send the measured results to the arbitrator,who uses the Lagrange interpolation formula to check whether the results can recover the original secret.

Table 3.Comparison of computational complexity in(t,n)threshold phase.

7.Conclusion

In this paper, we use a quantum secret sharing scheme based ond-level quantum Fourier transform and Lagrange interpolation, adding the threshold function to a quantum (t,n)threshold signature scheme and improving on the scheme.A true quantum(t,n)threshold signature scheme is formed.The improved scheme can resist forgery attack and collusion attack, and has non-repudiation.At the same time, it can reduce the trust of the arbitrator in the signature process.Finally,we not only compare the performance of our scheme with the original scheme, but also compare the (t,n) threshold secret sharing phase with corresponding recent schemes.The results show that the scheme in this paper reduces the consumption of resources.In this paper,we have designed only a theoretical scheme for quantum(t,n)threshold signature,the physical implementation of which is subject to further study.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.61771294 and 61972235).