Creation mechanism of electron–positron pair on equally spaced multiple localized fields

Chuan-Ke Li(李传可), Nan-Sheng Lin(林南省), Xian-Xian Zhou(周鲜鲜),Miao Jiang(江淼), and Ying-Jun Li(李英骏),,‡

1State Key Laboratory for GeoMechanics and Deep Underground Engineering,China University of Mining and Technology,Beijing 100083,China

2School of Science,China University of Mining and Technology,Beijing 100083,China

3School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu 233030,China

Keywords: electron-positron pair creation,ultra-strong laser field,computational quantum field theory

1.Introduction

Pair creation from the vacuum is a phenomenon where a vacuum in the presence of a supercritical electromagnetic field is unstable and decays into electron–positron pairs.[1,2]It may be the most intriguing prediction of quantum electrodynamics (QED) and has been studied with different methods since Dirac put forward the relativistic wave equation and predicted the existence of positrons.[3]In the 1930s, the pioneering research of the electron–positron pair creation induced by the ultra-strong field was engaged by Sauter,[4]Heisenberg and Euler.[5]Schwinger[6]formalized the pair creation process in the language of QED and recovered the pair creation rate in a constant electric field with the propertime method, so sometimes the tunneling pair creation is also called the Schwinger pair creation or the Schwinger effect.Brezin and Itzykson[7]extended the research to the vacuum pair creation in a time-dependent electric field with the Wentzel–Kramers–Brillouin(WKB)approximation and found the multi-photon pair creation process, which was different from the Schwinger tunneling process.Moreover, various methods are widely utilized in this field, such as the worldline instantons technique,[8–12]quantum kinetic theory,which includes the quantum Vlasov equation(QVE)[13–19]and realtime Dirac–Heisenberg–Wigner (DHW) formalism,[20–27]as well as computational quantum field theory (CQFT).[28–46]Recently, the relation between these methods has been explored.Dumlu[47]proved that the QVE is equivalent to the semiclassical scattering method in both scalar QED and spinor QED.Hebenstreitet al.[20]found that the Wigner function in spinor QED could be reduced to the QVE for a uniform and time-varying electric field with one component.Liet al.[27]generalized the above result to the scalar QED,and found that in this case the electric field could have three components.Liet al.[48]demonstrated theoretically that the CQFT is equivalent to the quantum kinetic theory for pair creation in a spaceindependent and time-inhomogeneous electric field.

The optical intensity in the focal region can be enhanced considerably by the tight focusing.[49,50]In 2021,Jinet al.[50]realized ultra-high intensity over 1023W/cm2by tightly focusing the CoReLS petaWatt(PW)laser.More exciting achievement is the ultra-high intensity and ultra-short laser facilities under construction, such as the Extreme Light Infrastructure(ELI)[51]in European,whose intensity is expected to be 1024–1026W/cm2.However, the critical field strength to generate a significant amount of pairs was estimated to be on the order of 1029W/cm2,which is stronger than these laser facilities by several orders of magnitude.[6]Partly motivated by these difficulties,Schützholdet al.proposed a dynamically assisted Schwinger mechanism,[10]by combination of a strong and slowly varying electric field and a weak and rapidly changing electromagnetic field.The dynamically assisted Schwinger mechanism shows a possibility to enhance the pair creation rate significantly and results in a decrease of the effective spectral gap between the positive continuous state and the Dirac sea.The scheme of simultaneous multiple pulses focusing on one spot from the structural features of the ELI facility has been proposed.[52–55]The field configuration leads to a significant reduction of the threshold energy needed for the pair creation to become observable compared to the case of one pulse.Suet al.designed a multifield configuration by applying several localized subcritical static electric fields side by side and lowered the threshold of pair creation with quantum tunneling.[30,34]

In this paper,we explore the process of electron–positron pair creation in the presence of multiple electric fields that vary in space and time.Specifically, we investigate the impact of the number of electric fields, their spatial separation,and their potential height on the probability of pair creation.Our findings offer valuable insights into the visualization and understanding of pair creation in multiple fields.Ultimately,this research provides theoretical reference for experiments of vacuum pair creation detection.

This paper is organized as follows.In order to render the presentation self-contained,Section 2 is devoted to a concise review of the theoretical framework of the computational quantum field theory.In Section 3,the electron–positron pair creation induced by multiple localized fields is investigated,and the results are discussed.In Section 4, we give our conclusions.

2.The theoretical framework of computational quantum field theory

To study the electron–positron pair creation process, the quantum field theory is necessary to understand the particle creation and annihilation.We introduce a time-dependent field operator ˆψ(t)and the Hamiltonian of quantum field theory ˆHto describe creation and annihilation processes.They obey the Heisenberg equation of motion,i∂ˆψ(t)/∂t=[ˆH, ˆψ(t)].However,we neglect the interfermionic interaction and treat external fields as classical in strong field approximation.Then,the Heisenberg equation is equivalent to the Dirac equation[28,56]

Here,cis the speed of light in vacuum,σ1andσ3are the Pauli matrices.The electric field is described by the scalar potentialV(z,t).In this paper we use atomic units,soc=137.036 a.u..The four-component Dirac spinor wave functions can be reduced to two components when the electric field is homogeneous in both thexandydirections.[28]The field operator ˆψ(z,t)can be expanded by field-free energy eigenstatesup(z)(E ≥c2)andun(z)(E ≤-c2)as

The electronic portion is defined asThen the spatial number density of electrons reads

and the momentum distribution reads

3.Numerical simulations and results

In the following,we consider several electric fields of the colliding laser pulses whose temporal and spatial variations are independent.Because the electric field is homogeneous inxandydirections,the electric field can be represented by the scalar potential

whereMis the number of fields,Vi(z) andf(t)θ(t) describe the spatial and temporal variations of the electric field,respectively.The spatial profile of the field is a Sauter potential acting along thezdirection

whereV0is the height of fields,W0is characteristic width,z0is the center of fields,anddis the distance of the adjacent field center.Typical configurations of the multiple fields are shown in Fig.1.

The temporal component includes two parts: a long-term oscillation

whereωis the frequency of the laser pulses, and a turn-on function

whereT=2π/ωis one laser period.In the numerical implementation, the scalar potential (the multiple Sauter potential,see Eq.(9))is modified by a pulse shape function consisting of sin2turn-on,and followed by a plateau region to avoid drastically switching on in time.

Fig.1.Schematic of the multiple fields for different distance d and fields number M:(a)a non-overlap field between two fields,(b)an overlap field between two fields, (c)a non-overlap field among four fields,and (d) an overlap field among four fields.The solid line represents a single field(SF),and the dotted line represents a combined field(CF).

3.1.Pair creation in the multiple equidistant fields

In this section, we study the electron–positron pair creation induced by multiple equidistant fields,as shown in Fig.1.The electron–positron pairs are created continuously at a constant rate for the reason thatω=2.5c2＞2c2(shown in Fig.2).Because the combined field strength is enhanced with increasing the number of fields,the created pair number grows significantly.

To enable a comparison of particle pair creation induced by multiple fields at different distances, we calculate the resulting number of pairsnMat 20 laser period, which is presented in Table 1.When the multiple electric fields completely overlap (d=0), the total strength ofMlaser fields isMtimes of a single field, i.e.,EM=ME1.Brezin and Itzykson used the Wentzel–Kramers–Brillouin(WKB)approximation to analyze the creation of positron-electron pairs through multi-photon absorption processes,and also found that the creation rateΓis directly proportional to the square of the field strength.[7]It is reasonable that the particle pairs created by the oscillating field are quadratically related to the total field strength whend=0.However,it is under a different scenario when the multiple fields are well separated(d ≥W0).We have found that the number of total pairs,nM, depends linearly onn1.The slope of functionnM(M) is reduced significantly by increasing the distanced.For instance, the linear relationships arenM=0.0548(M-1)+n1,nM=0.032(M-1)+n1,andnM=0.02457(M-1)+n1for the distancesd=W0,2W0,and 3W0,respectively.The linear relationship between the pair creation in multiple fields and a single field is weakened as the distancedincreases.The creation of pairs in the multiple fields becomes mutually influenced in space when the distance between the fields is greater than the characteristic widthW0.Although the effect weakens as the distance between the fields increases,the presence of other fields continues to impact the pair creation process of each field.The energy distribution of the pairs exhibits oscillatory behavior,which is due to the interference of the created particles from localized fields.[32]As the distancedapproaches infinity, the energy distribution becomes much wider and only exhibits a single peak atE=ω/2 due to the symmetry,and the total numbernMapproachesMn1.

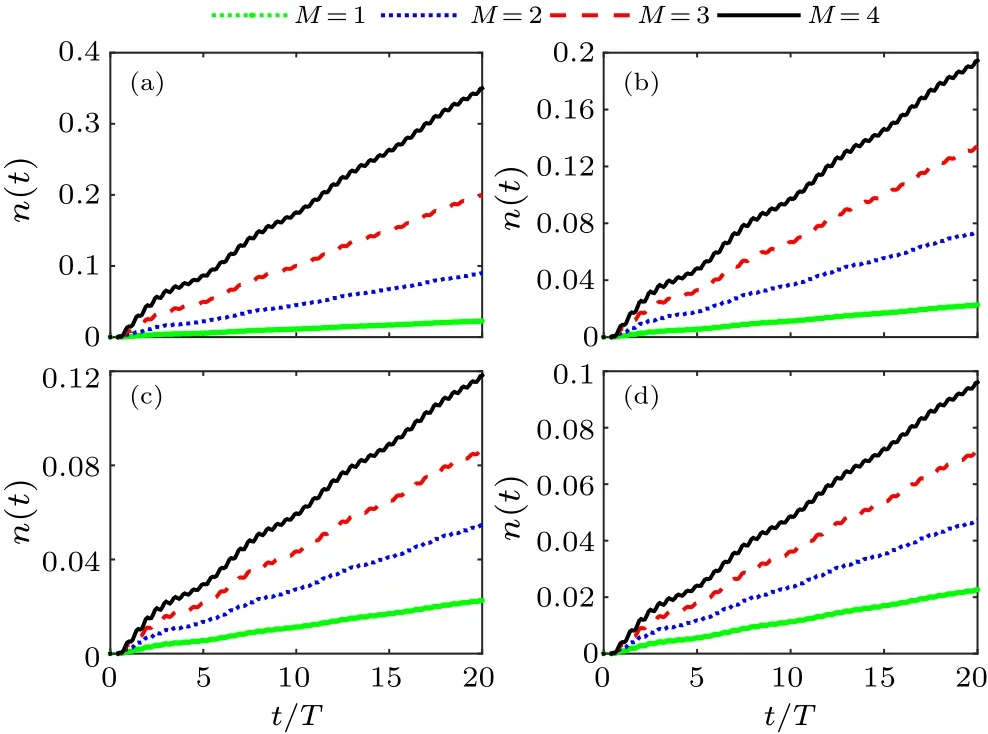
Fig.2.Evolving number of the electron–positron pairs for the different distance between fields: (a) d =0, (b)W0, (c) 2W0, and (d) 3W0.The green dot-dashed line,the blue dotted line,the red dashed line and the black solid line represent M =1, 2, 3 and 4, respectively.Here,V0 =0.3c2,W0 =3/c,and ω =2.5c2.The time is in units of the laser period T =2π/ω.

Table 1.The number of created pairs at 20 laser periods for different distance between fields d and fields number M.

In our model, the height of the electric potential corresponds to the oscillating field’s amplitude.There is a corresponding increase in the number of pairs created as the height of the electric potential increases, as shown in Fig.3.We increase the original potential heightV0by factors of 1.6 and 2 from 0.3c2to 0.48c2and 0.6c2.The field strength is determined by the spatial derivative of the scalar potential(E(z,t)=∂V(z,t)/∂z),and it leads to the strengthE0=V0/2W0,where 2W0is the effective field width.The electric field strengthEis proportional to the heightV0whenW0stays the same.According to the relationshipΓ∝E2, the creation rates have increased up to 2.56 times and 4 times, respectively.This means that the rate of pair creation has significantly increased with the increment of the electric field strength.Figure 3(a)presents the number of pairs created by a single field, with creation rates shown for potential heights of 0.3c2(8.41 a.u.),0.48c2(21.45 a.u.),and 0.6c2(33.40 a.u.).The creation rates of electron–positron pairs for two fields are listed in Table 2.These results show that the creation rate is directly proportional to the square of the field strength.

Table 2.The creation rates of electron–positron pairs for different distances between fields d.

Fig.3.Evolution of the number of electron–positron pairs for different distances between fields and the number of fields: (a) d =0, M =1,(b) d =0, M =2, (c) d =W0, M =2, and (d) d =2W0, M =2.The blue dotted line, the red dashed line, and the black solid line represent V0 =0.3c2, 0.48c2, and 0.6c2, respectively.Here,W0 =3/c and ω =2.5c2.The time is in units of the laser period T =2π/ω.

3.2.Pair creation’s spatial dependence

In the preceding section,we investigate pair creation from multiple fields with equal distance.Additionally,we have analyzed the influence of different distance between two fields on pair creation process in this section.The two fields are partially overlapped, i.e.,d ≤W0.We assume that the electron–positron pairs created by the oscillating field are homogeneous in the field region considering the dipole approximation.[13–19]We first neglect the interference effects to explore the impact of overlapping extent on pair creation.Here,we introduce the reduced pair numbern′M=nM/W.Because two fields completely overlapping will double the field strength,the reduced pair number of two fieldsn′2=4n′1whend=0.Sketch of the potential is presented to clearly indicate overlapped and nonoverlapped regions,as shown in Fig.4.The hypothesis of the homogeneous pair creation rate leads to five different spatial regions in the configuration.The regimes I and V are zero field area and no pairs are created there.The reduced pair number isn′1in the regions II and IV,while the reduced pair number is 4n′1in the overlapped region(III).From Fig.4,the total number of two fieldsn2=(W0-d)n′2+2dn′1=(4-2d/W0)n1.Therefore, the pair number is linearly relative to the distance between two fields if we have the homogeneous creation hypothesis.However, the pair numbern2has a parabolic-like relationship with the distancedin our simulation results, as shown in Fig.5.The pair creation must be inhomogeneous in space even with constant field strength,and the dipole approximation is invalid,because the characteristic length of the pair processlcis not far smaller than the laser wavelengthλ.[19]Consequently,the pair creation process is space-dependent in the interaction region.

Fig.4.Schematic of combined field between two fields.The blue solid and the red solid denote the left field and right field, respectively.The black dotted line denotes the combined field.

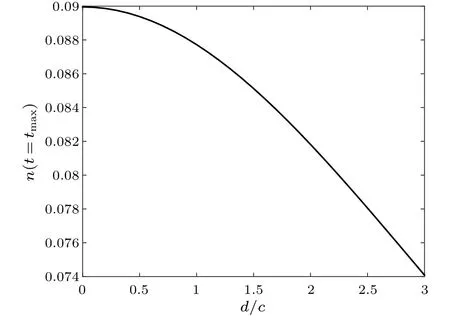
Fig.5.Dependence of the created pair number on the distance between two fields.Here,V0=0.3c2,W0=3/c,ω =2.5c2,and tmax=20T.

To mitigate the influence of the motion of the created pairs,we evaluate the spatial distribution of pairs at timet=T.As shown in Fig.6, the spatial distribution is both Gaussian and biased, presenting the inhomogeneity of pair creation in an oscillating field.

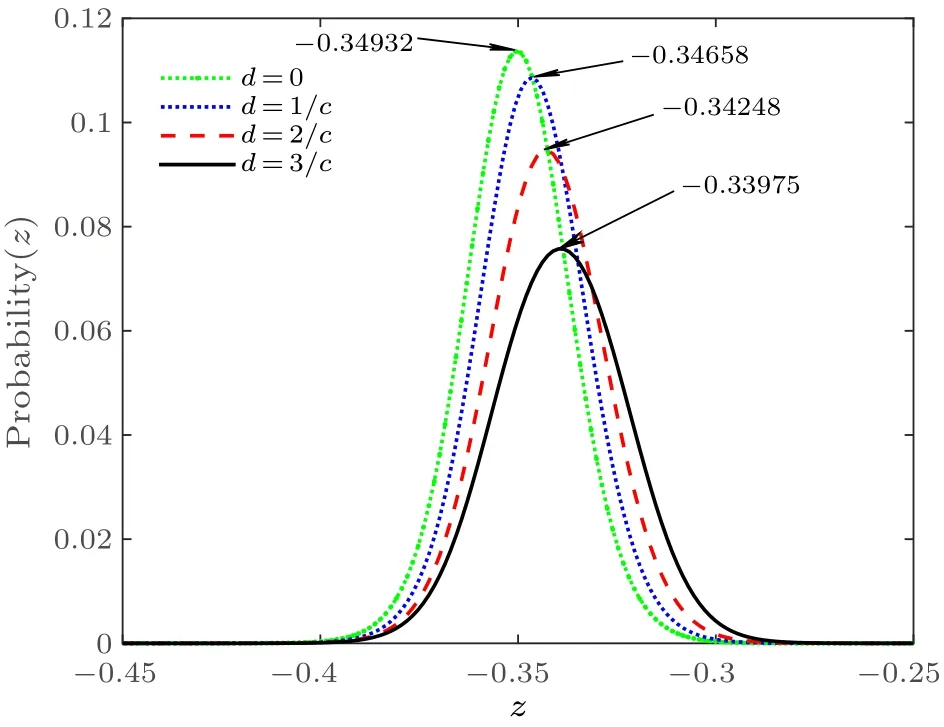
Fig.6.Spatial distribution of the created pairs for different distances.The green dot-dashed line,the blue dotted line,the red dashed line,and the black solid line represent d =0, d =1/c, d =2/c, and d =3/c,respectively.Here,V0=0.3c2,W0=3/c,ω =2.5c2 and t=T.

Fig.7.Strength of the field at the center versus the distance between two fields.Here,V0=0.3c2 and W0=3/c.

Moreover, the peak of the spatial distribution is defined by the maximum of created pairs.We find that the peak of the spatial distribution is shifted to the right with increasing the distance,as shown in Fig.6.The displacement of the peak Δz=d/2.The peak locates at the combined field center which is at-0.34932,-0.34658,-0.34248,and-0.33838.Therefore, we can conclude that the field center is the most pair creation zone.In addition,the peak of the spatial distribution becomes smaller as the distance between two fields increases(see Fig.6).The peak height depends deeply on the strength of field centerE0,which is defined by the partial derivative of the electric potential with respect toz(i.e.,E0=∂V(z,t)/∂z|z=z0).With the increment of the distance between two fields,E0becomes smaller (see Fig.7) in the reason that Sauter-like potential has a long tail with an exponential decay,and it results in the decrement of the peak height.Hence,the pairs creation process is inhomogeneous in the field region,and the electron–positron pairs are mainly created in the zone of strong strength.

4.Conclusion

In summary, we have realized that multiple equally spaced identical electric fields would lead to a significant electron–positron pair creation.The creation rate of pairs is directly proportional to the square of the electric field strength on a weak and rapidly altering field.In studying the process of the creation by multiple adjacent fields,we notice that the creation rate exhibits different behaviors when the fields overlap or not.The number of particle pairs created in the case of completely overlapping multiple electric fields isM2times higher than that of a single field because the total field strength is enhanced by a factor ofM.When the fields do not overlap, the number of created pairs increases linearly with the number of fields.However,because there is mutual interference,the total number exceeds the sum of the fields alone, i.e.,Mtimes of that created by a single field.The in-depth study of the above two cases demonstrates the inhomogeneous creation rate in the interaction region,and the pair creation is concentrated in the central region where the field strength is strongest.Therefore,when multiple fields exist simultaneously,whether they overlap results in the stronger field in some regions, which dominates the final number of particles created.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos.11974419, 11605286,and 12204001)and the National Key R&D Program of China(Grant No.2018YFA0404802).