Crysformer: An attention-based graph neural network for properties prediction of crystals

Tian Wang(王田), Jiahui Chen(陈家辉), Jing Teng(滕婧), Jingang Shi(史金钢),Xinhua Zeng(曾新华), and Hichem Snoussi

1Institute of Artificial Intelligence,SKLSDE,Beihang University,Beijing 100191,China

2Zhongguancun Laboratory,Beijing 100191,China

3School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China

4School of Control and Computer Engineering,North China Electric Power University,Beijing 102206,China

5School of Software Engineering,Xi’an Jiaotong University,Xi’an 710049,China

6Academy for Engineering and Technology,Fudan University,Shanghai 200433,China

7Charles Delaunay Institute,University of Technology of Troyes,Troyes Cedex 10004,France

Keywords: deep learning,property prediction,crystal,attention networks

1.Introduction

The prediction of crystal properties has gained significant interest in various fields, including materials science, chemistry, and solid-state physics,[1–3]due to its potential to enable the design and discovery of new materials with desired properties.[4,5]This has broad implications for diverse applications,ranging from energy storage to drug discovery.Traditional methods for predicting crystal properties typically rely on handcrafted features and domain-specific rules,which may have limitations in accuracy and generalization capability.[6,7]Consequently, there is growing interest in leveraging deep learning methods to improve the accuracy and efficiency of crystal property prediction.[5,8,9]Such approaches have the potential to overcome the limitations of traditional methods and provide more accurate and generalizable predictions of crystal properties, facilitating the discovery of novel materials with desirable properties.[10–12]

In recent years,deep learning has shown remarkable success in various fields,[13]including image recognition,natural language processing, and speech recognition.[14–17]Among the various architectures, transformer-based models have gained widespread attention for their ability to model complex dependencies effectively.[18–20]The transformer model,which uses the self-attention and cross-attention mechanism, has achieved state-of-the-art performance in diverse tasks.[17,18]These advancements in deep learning models have the potential to capture the intricate relationships among atoms in the crystal structure, which are essential for accurately predicting crystal properties.By leveraging the power of transformer-based architectures, researchers focus on modeling the complex interactions and dependencies among atoms,leading to more accurate and reliable predictions of crystal properties.[19,20]

In this paper,we present a novel deep learning-based approach based on deep learning for predicting the properties of crystal materials, utilizing a transformer-based architecture.Consistent with prior research, we represent a crystal structure by constructing both a graph and a line graph,[21–24]which respectively models the topological relations between atoms and bonds, and bonds and angles.Our model alternates between these two graphs via attention calculation in a transformer, updating the information of atoms, bonds, and angles.We leverage the power of attention mechanism during the message passing process to capture adaptive dependencies among atoms in the crystal lattice, resulting in more accurate predictions compared to traditional methods.[25–27]To control information propagation within the crystal graph,we introduce two attention mechanisms.[17,28,29]The first is cross-attention, which enables edges to receive information from the nodes they connect.The second is a conditionalattention mechanism that simulates interactions between two nodes under the control of their edge.Incorporating these attention mechanisms in a transformer network yields an improved graph neural network.We conduct extensive experiments on multiple benchmark datasets to evaluate the effectiveness of our approach,and compare our results to state-ofthe-art methods.Our findings demonstrate the superior performance of our method in terms of prediction accuracy and generalization capability.These results highlight the potential of deep learning-based approaches, specifically transformerbased architectures, for accelerating material design and discovery processes.

2.Method

In this section, we present our approach in accordance with the processing pipeline.We begin by elucidating the construction of crystal graphs,which constitute the input data for our model.The crystal graphs are composed of an atomistic graph and an atomistic line graph.Next, we explicate the architecture of our model, which takes the crystal graphs as input,extracts the corresponding features,and ultimately delivers the prediction results.

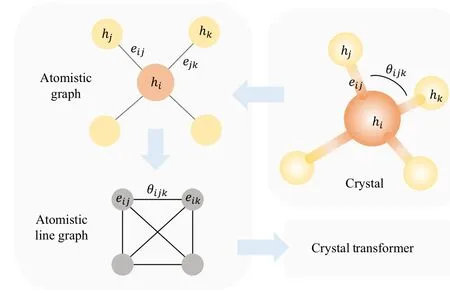
Fig.1.The processing pipeline.The atomistic graph is first constructed from the crystal structure and an atomistic line graph is derived, both of which are fed into the crystal transformer to obtain the representation of the crystal and finally to make predictions.

2.1.Construction of crystal graphs

Translational and rotational invariance is essential for describing the structure of a crystal.[22,23]To meet these requirements,we utilize a graph to represent the crystal structure.In this graph, the nodes represent atoms, while the edges correspond to the bonds connecting two atoms.The connectivity between atoms is determined by the following,[23,24]wherein each atom is considered connected to its 12 nearest neighbors in a periodic manner.

While the above graphs capture the connectivity and distance information of the crystal structure,we construct another graph to incorporate additional structural details.Inspired by Ref.[24], we introduce the concept of line graphs, which are derived from the original graphs.In the line graph,the nodes correspond to the edges in the original graph,while the edges denote the relationships between two edges.

To differentiate between the above two graphs,we name them the atomistic graph and atomistic line graph, denoting them asGandGL, respectively.In the atomistic graph, the node feature represents the atomic number,while the edge feature represents the bond length.In the atomistic line graph,the nodes share features with the edges in the atomistic graph,as both of them represent the bonds in the crystal.The edge feature in the atomistic line graph denotes the bond angle.

2.2.Feature embedding module

The two graphs consist of three types of features: atomic numbers, bond distances, and bond angles.To facilitate their use in the modeling process, we adopt a feature embedding module that transforms these scalar features into corresponding vectors.

For the atomic featureh, we use an embedding matrix to map the discrete atomic number to a vector representation of dimensionalityd.In contrast, for the bond distances and bond angles, we first project the scalar values onto a lowerdimensional vector space (e.g., 64 dimensions) using a radial basis function (RBF) expansion (e.g., a Gaussian kernel function).Subsequently, we employ a linear transformation to project these lower-dimensional vectors onto a highdimensional space.

Fig.2.A Crysformer layer consists of (i) a cross-attention module to update the node features,(ii)a conditional-attention module for updating both node and edge features,and(iii)two feed-forward networks.

2.3.Crystal transformer layer

The crystal transformer layer is an attention-based module that updates both node and edge features, as shown in Fig.2.The updating process comprises three distinct steps:(i) interactions between nodes and edges, (ii) message passing between nodes with connections,and(iii)the feed-forward networks.[17]Accordingly,we have designed two separate attention modules,each of which corresponds to one of the two interaction processes.

2.3.1.Cross-attention module

In the first step,we update the nodes based on the edges to which they are connected.To selectively aggregate edge information to the nodes,we employ a cross-attention mechanism.We use the node features as the queries and the edge features as the keys and values.The cross-attention mechanism is formulated by

wherehi ∈Rdrepresents a node feature,ei j ∈Rddenotes the feature of the edge between nodeiandj, andNirefers to a set of nodes connected to nodei.The importance ofeijfor nodeiis determined byαi j,which is obtained by the dot product ofWqhiandWkei jdivided bydk.Here,Wq,Wk,andWvare learned weight matrices with appropriate dimensions,anddkrepresents the dimension ofWkei j.The updated node feature ˆhiis calculated by adding the weighted sum of edge features to the original node feature with a normalization.The cross-attention mechanism allows the nodes to aggregate significant information from the edges.Through cross-attention,the nodes receive edge information and update themselves.

2.3.2.Conditional-attention module

In the second step,we aim to facilitate the interaction between nodes that are connected by edges.We consider that the nature of the edges plays a crucial role in this interaction; for instance,edges connecting nodes that are in close proximity to each other are expected to have a stronger influence on their interaction.Drawing inspiration from gated neural networks,we propose a conditional-attention mechanism to model the impact of the edges on the interaction.The conditional-attention mechanism is defined by Eq.(3),wherein we compute the importance factor of nodejfor nodeiwhile conditioning on the edge featureeij

We subsequently update the node features by adding the weighted sum of the features of its neighboring nodes,which is normalized to account for differences in scale.Furthermore,the edge features are updated by taking into account the importance factor that captures the relation between the two nodes.

2.3.3.Layer architecture

We have incorporated the two attention modules into the transformer architecture,whereby a feed-forward network(FFN)is applied after updating the nodes and edges.This FFN is formulated by a two-layer linear transformation followed by an intermediate activation function such as ReLU:

We have adopted a multi-head mechanism, as suggested by Refs.[17,26],to enhance the model’s representation.

In one layer of Crysformer,the designed attention mechanism allows the model to selectively focus on relevant nodes or edges and their surrounding environment, thereby improving the representation learning.

2.4.Crystal transformer

Building upon the aforementioned modules,we introduce a novel framework for predicting the properties of crystals,named crystal transformer (Crysformer).Crysformer comprises three major components: (i)a feature embedding layer,(ii)Nsuccessive Crysformer blocks,and(iii)an output module for prediction.

As shown in Fig.3, each Crysformer block contains a Crysformer layer on the atomistic line graph along with another Crysformer layer on the atomistic graph.To prevent confusion between the node and edge features of the two graphs,we denote atom, bond, and angle representations ash,e, andt, respectively.The first Crysformer layer takes the bond and angle features as inputs and updates them on the line graphs.The updated bond features are then forwarded to the second Crysformer layer, along with the atom features,and the layer yields the updated representations.The overall algorithmic description of Crysformer is outlined in Algorithm 1.

Fig.3.Crysformer architecture.Crysformer consists of(i)a feature embedding layer for projecting the input features, (ii) N successive Crysformer blocks to update the representations, and (iii) an output module for prediction.

Algorithm 1 Algorithm in Crysformer Input: atomistic graph G,atomistic line graph GL,atomic number h0,bond distance e0,bond angle t0.Output: Output prediction Y ∈R1.1: {Feature embedding layer:}2: h ∈Rd ←Embedding(h0)3: e ∈Rd ←We·RBF(e0)+be 4: t ∈Rd ←Wt·RBF(t0)+bt 5: {Continuous Crysformer Blocks:}6: for l=1,2,...,N do 7: e,t ←CrysformerLayer(GL,e,t)8: h,e ←CrysformerLayer(G,h,e)9: end for 10: {Output module:}11: Y ←MLP( 1||h||∑h)

Table 1 presents the hyperparameters of the Crysformer.We minimize the mean squared error(MSE)loss when training the models.We train all models for 300 epochs using the AdamW optimizer[29]with normalized weight decay of 10-4and a batch size of 64.

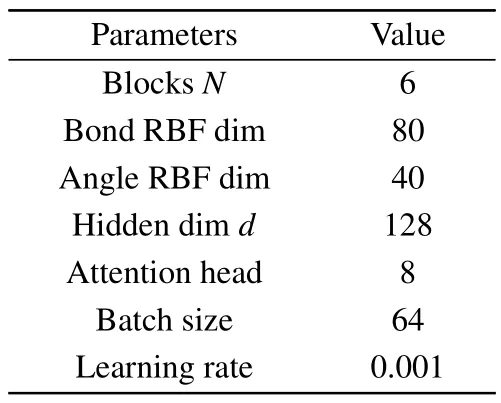
Table 1.Crysformer model configuration.

3.Results

3.1.Dataset

To evaluate the performance of our Crysformer, we conducted experiments on two solid-state property datasets, Materials Project[30]and JARVIS-DFT.[31]In order to ensure comparability with previous research, we utilized versioned snapshots of the datasets.Specifically, we employed the MP 2018.6.1 version (MP-2018), which contains 69239 materials with critical properties such as Perdew–Burke–Ernzerhof functional (PBE) bandgaps and formation energies.We also utilized the JARVIS-DFT dataset with the 2021.8.18 version,comprising 55722 materials with essential properties, such as van der Waals correction with optimized Becke88 functional(OptB88vdW)bandgaps and formation energies.These properties are fundamental for designing functional materials.To facilitate direct comparison with previous works,[22–24]we employed train–validation–test splits of 60000–5000–4239 for the MP dataset and 80%–10%–10%for the JARVIS-DFT dataset and its properties.

3.2.Model performance

Table 2 presents the performance of Crysformer models on MP-2018, specifically in terms of the mean absolute error(MAE) metric.We compare the performance with CFID,[5]CGCNN,[22]MEGNET[23]and ALIGNN.[24]The best MAE results obtained by Crysformer for formation energy(Ef)and band gap (Eg) are 0.022 eV/atom and 0.196 eV, respectively.Since each property has different units and variances,we also report the mean absolute deviation(MAD)for each property to ensure an unbiased comparison of model performance across different properties.The MAD values represent the performance of a random guessing model with an average value prediction for each data point.

Table 3 presents the performance of our model on different properties of the JARVIS-DFT database.The differences between the JARVIS and MP datasets arise from the use of different computational methods, such as distinct functionals (PBE vs.OptB88vdW), the application of the DFT+U method, and various DFT hyperparameter settings like smearing andk-point settings.Additionally,data distribution could be another potential factor.However,despite these differences,our model demonstrates good performance on the JARVIS dataset and achieves competitive results.Specifically,for the prediction of bandgap (OPT) and total energy, our Crysformer obtains MAE values of 0.137 eV and 0.035 eV,respectively.

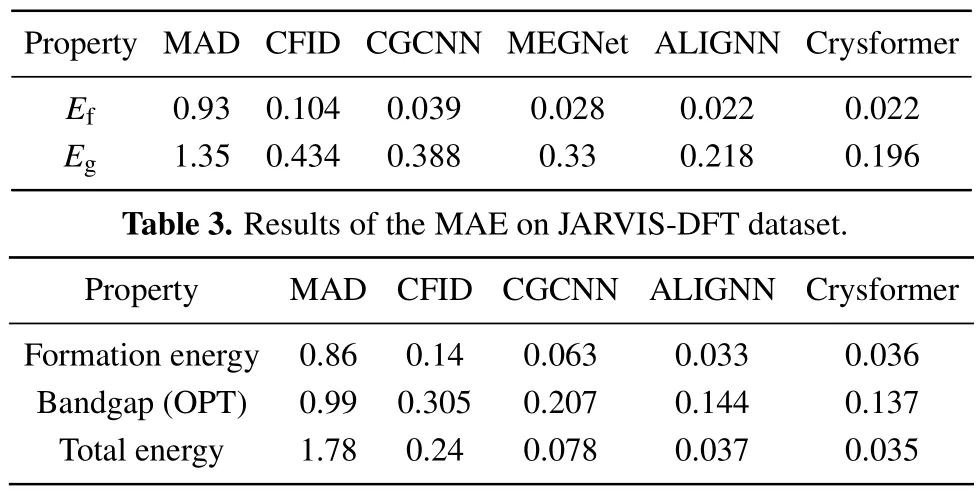
Table 2.Results of the MAE on MP-2018 dataset.

3.3.Model analysis

3.3.1.Learning curves

We illustrate the training progress of the Crysformer by plotting its learning curves.As depicted in Fig.4,the training loss of the model exhibits a decreasing trend as the number of iterations increases, concurrently leading to a decrease in the error rate of the validation set.However,it should be noted that the model is subject to overfitting, as evidenced by the considerable disparity between the error rate of the training set and that of the validation set.

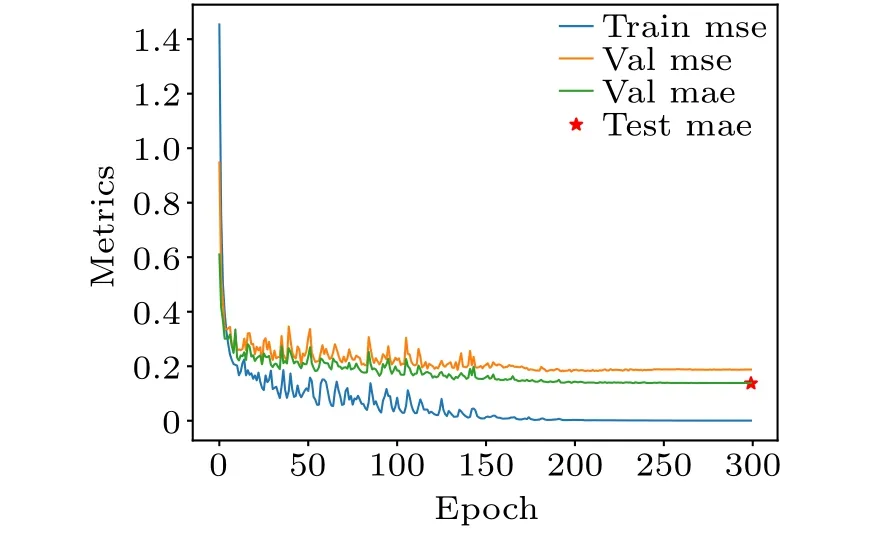
Fig.4.Learning curves of Crysformer.We visualize the metrics during the training for JARVIS-DFT OptB88vdW bandgaps.The loss is gradually decreasing and is accompanied by some over-fitting.

3.3.2.Ablation analysis

In Table 4,we vary the hyperparameters of our model,including the numbers of blocks,hidden dimensions,and numbers of heads, for JARVIS-DFT OptB88vdW bandgaps.We find that increasing the model size,such as increasing the number of blocks or model dimension, can lead to more accurate predictions,but also increase the computational burden.Considering the trade-off of speed and accuracy, we choose the experimental settings in Table 1 as the default.

We ablate the proposed attention components to evaluate their contribution to the overall architecture.As shown in Table 5, no interaction of nodes and edges results in training failure.Using only one of the two attention methods leads to a decrease in accuracy, which shows that our proposed module is effective.Further,we observe that conditional-attention has a greater impact on the results,suggesting that the interaction between nodes is more important.

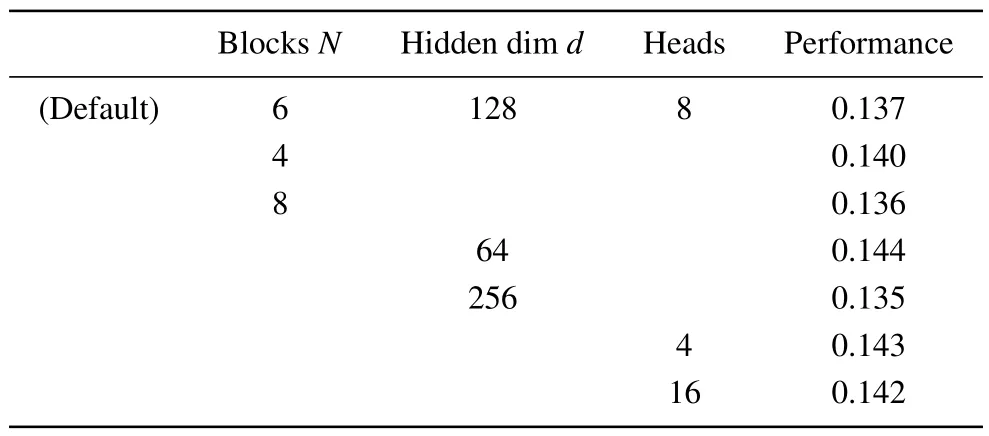
Table 4.Hyperparameters tuning.

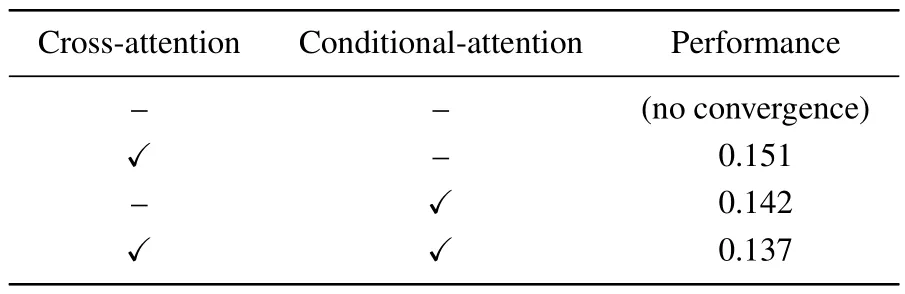
Table 5.Component ablations.

4.Discussion and conclusion

We have presented Crysformer, a novel deep learning framework based on graph networks for accurately predicting the properties of crystals.By leveraging attentional mechanisms,we have demonstrated the ability to construct a unified model that adaptively focuses on valuable information,resulting in improved representations and better predictive accuracy for various solid-state properties.Our models have been evaluated on two different solid-state property datasets,MP-2018 and JARVIS-DFT, and achieved state-of-the-art performance for most properties in both datasets.

We believe that our work represents a step forward in the development of artificial intelligence for industrial and scientific purposes, especially in the field of materials science.The accurate prediction of material properties is critical for the design of functional materials with desired properties.Our graph-based approach provides a natural framework for representing the complex structural information in crystals and can be used as a universal building block for developing accurate prediction models.

We have demonstrated that the use of deep neural networks and graph networks is an effective approach for predicting the properties of crystals.Our Crysformer models provide improved accuracy over prior models in most properties for crystals, and we expect our work to facilitate future research in this area.We hope that our contribution will inspire further development of artificial intelligence and graph-based methods for materials science and related fields.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.61972016 and 62032016)and the Beijing Nova Program(Grant No.20220484106).