Anti-Stokes/Stokes temperature calibration and its application in laser-heating diamond anvil cells

Minmin Zhao(赵旻旻), Binbin Wu(吴彬彬), Jingyi Liu(刘静仪), and Li Lei(雷力)

Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China

Keywords: Stokes/anti-Stokes Raman spectroscopy,temperature calibration,laser-heating diamond anvil cell(LHDAC),anharmonic effect

1.Introduction

The high-pressure, high-temperature (HPHT)in-situmeasurement technology is helpful for us to discover new phenomena and effects that cannot be obtained under ambient conditions and has important research significance in the study of superconductivity,planetary interior environment,geoscience and so on.In a diamond anvil cell(DAC)experiment,laser-and resistance-heating are the two major methods for elevating the temperature of a sample under experimental conditions involving high pressure.The resistance heating,including external resistance[1]and internal resistance,[2]has a typical heating temperature belowT～2000 K due to technical limitations.[2]For comparison,laser-heating diamond anvil cell(LHDAC)technology can be applied in a wide range ofP–Tfields:P ＞200 GPa andT=1200–6700 K.[3]With the technology development of LHDAC,high-pressure science has attained new developments in the past two decades.[4–6]Accurate temperature calibration is of great significance for a LHDAC experiment.The temperature calibration in the process of laser heating, however, is a complex technical problem,involving thermal radiation, thermal fluctuation, and spatial and spectral resolutions.The conventional thermometry in LHDACs consists of spectroradiometry,[7–9]thermocouple[10]and anti-Stokes/Stokes methods.[11,12]The spectroradiometry method is based on the Planck radiation function, and its measurement accuracy (at least±10%) is affected by the wavelength dependence of the emissivity and by the optical aberration of the system.[7]One of the critical challenges remains the process of data collection at temperatures belowT～1000 K.This is generally due to the relatively low photonemissivity and spectral resolutions.Due to the mean thermal field measurement,accurate measurement of specific sample points cannot be guaranteed.The spatial resolution of spectroradiometry is limited, even in the case of adding spatial filtering in front of the spectrometer.The thermocouple method exhibits an important number of limitations.It is generally unable to track the rapid temperature changes and cannot accurately scale the temperature of samplesin-situin the DACs.Further, this method is generally not compatible with the small culet-size anvil DACs (such as 50 μm culet size).Anti-Stokes/Stokes thermometry is based on the anti-Stokes line and Stokes line of the sample itself.Using this thermometry technology,studies have been carried out on the high-pressure Raman spectra of liquid H2(D2),[10]the melting line of fluid N2,[13]the kinetic barrier of phase transition in CO2,[14]etc.However, the principal formula was adopted in the thermometry,and the calibration parameters of the system in the formula have not been considered.Therefore,the application of anti-Stokes/Stokes thermometry is still in its infancy.The anti-Stokes/Stokes temperature calibration has not been extensively performed,and the correction factor,γ,of the system has not been studied in detail in previous studies.Here we present a detailed study on anti-Stokes/Stokes temperature calibration in the LHDAC system,where the high-pressure anharmonic behaviors of diamond and hBN have also been studied.

2.Theoretical considerations

Spontaneous Raman scattering is divided into Stokes Raman scattering and anti-Stokes Raman scattering.The anti-Stokes/Stokes thermometry principle is based on the detailed balance principle of Stokes and anti-Stokes line intensity asymmetry, using the strength ratio of the anti-Stokes line to the Stokes line measured by Raman spectroscopy to obtain thein-situtemperature of the sample.The incident photon is scattered by phonons, emits or absorbs a phonon in the lattice,and the direction of the wave vector is determined by the difference between the incident direction and the scattering direction vector of the photon (Fig.1(b)).Under experimental conditions involving thermodynamic equilibrium, the microscopic particles are usually in the intrinsic motion state with specific energy and are arranged into different energy states following the Boltzmann distribution.The Boltzmann distribution is a dynamic distribution,in which particles constantly jump between different energy levels,absorbing and emitting photons.The frequency of Stokes line is lower than the frequency of exciting light,and the frequency of the anti-Stokes line is higher than the frequency of exciting light.[15]The relative occupancy rates of the ground state and the excited state in thermal equilibrium can be derived from the Boltzmann distribution,,whereTis the absolute temperature,viis the transition energy wave number between the excited and the ground state.With the increase of temperature, the intensity of anti-Stokes line increases and the intensity of Stokes line decreases.This trend increases significantly with the increase of the temperature,and agrees well with the Boltzmann distribution law as described by the following equation:[16]

Fig.1.(a) Diagram of energy level transitions of Rayleigh scattering,Stokes scattering and anti-Stokes scattering.(b) The relationship between photon scattering and wave vector.

whereIASandISare the intensities of anti-Stokes and Stokes lines,respectively.ν0andνirefer to the Raman shift(in cm-1)of Raman exciting laser and the temperature-dependent Raman mode (in cm-1), respectively.cis the speed of light,his Planck’s constant,kis the Boltzmann constant andTis the absolute temperature (K).Raman laser power, accumulation time and other factors were changed to precisely measure the intensity ratio of anti-Stokes to Stokes Raman scattering.

3.Technical considerations

The anti-Stokes/Stokes technique of thermometry has many obvious advantages.First, the functional relationship between Raman scattering intensity ratio and temperature is not affected by external compression,internal stress and sample fluorescence, this observation highlights its suitability for LHDAC experiments.Second, the identification of this parameter is only based on the anti-Stokes and Stokes lines of the tested samples, which could improve the spatial resolution of the measurement.Third,this method can be applied to solid, gas, and liquid samples,[11,14,17]and is suitable for acquisitions at relatively low temperatures,withTranging from 300 K to 1000 K.Fourth, the anvil diamond temperature can also be measured at the same time to verify its heating and insulation efficiency.

However, despite the aforementioned advantages, we could also see that due to the weakness of anti-Stokes signal, only the Stokes scattering line is conventionally used in Raman spectroscopy.Further, the sample size in the DACs is particularly small (typically, 10–50 μm), raising higher requirements for the spatial resolution and sensitivity of the experimental setup.This makes the measurement of anti-Stokes/Stokes temperature parameters more difficult in the LHDAC experiments.Previous works have shown that anti-Stokes/Stokes thermometry can be employed under experimental conditions involving atmospheric pressure.[18–20]This technique has however been rarely applied in a LHDAC system under HPHT conditions.[13,21]In addition, the anti-Stokes/Stokes thermometry is strongly dependent on specific experimental settings, including the Raman spectrometer, excitation laser wavelength,CCD,and so on.Strictly speaking,before the application of the anti-Stokes/Stokes temperature method,it is necessary to carry out a comprehensive temperature calibration.

4.Experimental setup

Stokes and anti-Stokes signs were detected in backscattering geometry (from the top side of the sample) using a 532 nm (RGB Nova Pro, 300 mW) and 633 nm (Cobolt 08-NLD,30 mW)laser for the Raman excitation.The spectrometer (Andor SR-303i-B) was composed of 1800 g/mm holographic grating with a resolution of 0.5 cm-1and electron gain EMCCD (Andor DU970P-BVF).The objective lenses employed in this work were a Mitutoyo M Plan Apo SL 20×(WD=34 mm, N.A.=0.28) (the scattering light receiving lens), and a Mitutoyo M Plan Apo NIR 5×(WD=37.5 mm,N.A.=0.14)(the laser heating objective lens).Further, Semrock NF03-633E-25 and NF03-532E-25 were the notch filters employed for anti-Stokes and Stokes scattering.Laser heating experiments were conducted with one 1064 nm CW fiber laser with a maximum power of 50 W and a spot diameter of about 50 μm.The system setup is shown in Fig.2.In this experiment,spectral analysis software Peakfit was used for data fitting.Both anti-Stokes and Stokes lines were fitted by the Voigt function after noise removal and characterized by Raman frequency(ν)and FWHM(Γ).

Fig.2.Self-designed optical system layout: (a)schematic diagram and(b)physical picture.

Fig.3.(a)Custom-build thermocouple thermometer coupling with 1064 nm laser heating,(b)typical Stokes and anti-Stokes Raman spectra of hBN at 1565 K under the 633 nm excitation light source,(c)LHDAC sample assembly schematic,and(d)a typical microphotograph of hBN upon laser heating.

In order to calibrate the anti-Stokes/Stokes temperature,a resistance-heating stage (THMS600, Linkam) was chosen for the temperature calibration in theT-range from 300 K to 800 K, with the temperature accuracy being±0.1 K (during the anti-Stokes/Stokes Raman measurements).The anti-Stokes/Stokes temperature results were calibrated with the Linkam resistance-heating stage.For temperature values aboveT～800 K, a custom-built thermocouple thermometer coupling with a 1064 nm laser heating was adopted(Fig.3(a)).In this method, a sample cavity was created by prepressing with a 500 μm-culet-size diamond anvil onto the metal junction of the thermocouple(K-type or B-type),with the sample placed within the cavity.A 1064 nm laser was used to heat the sample cavity from the bottom of the thermocouple, with the Raman laser being focused on the sample from the top of the cavity.The sample’s cavity temperature was directly measured by the thermocouple(at atmospheric pressure),while the anti-Stokes/Stokes temperature results were mutually verified with the thermocouple temperatures.

The thermometry data (from the Linkam resistanceheating stage and thermocouple thermometer)were compared with the anti-Stokes/Stokes temperature data, and the correction factorγwas introduced to correct the anti-Stokes/Stokes intensity ratio curve of Eq.(1).The maximum temperature calibration could be raised to above 1500 K.It should be noted that the two calibration methods are consistent with the Raman intensity ratio within the same temperature range(belowT～800 K).

Mao–Bell type DACs equipped with 500 μm culet sizes were applied to generate pressure.The pressure was determined by the ruby luminescence.[22]A 1064 nm NIR laser incident beam was used to heat the sample from the bottom of the DAC anvil.To ensure a good and stable heating and insulation efficiency,5 μm NaCl insulation layers were coated on each side of the diamond anvils, and Pt (～5 μm) was inserted within the sample’s cavity as the laser absorber.In the dataset presented in this work, the maximum temperature of the assembly could be raised to aboutT～1000 K(Fig.3(c)).

More than 20 high-temperature and high-pressure Raman experiments and more than 10 atmospheric high-temperature Raman experiments at ambient pressure were carried out.

5.Temperature calibration

Figure 4 shows the temperature-dependent Stokes and anti-Stokes Raman scattering for hBN and diamond with different laser excitation.The temperature values in Fig.4 were probed by employing the thermocouple.Below 800 K is generated by the way of resistance heating,above 800 K by laser heating.As the temperature rose,Raman lines were redshifted and their width increased; the intensity of the anti-Stokes lines enhanced distinctly(above 400 K)while the Stokes lines weakened(see Fig.4).

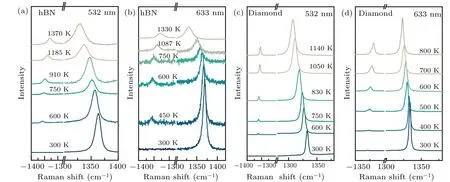
Fig.4.Temperature-dependent Stokes and anti-Stokes Raman scattering.(a) hBN under the 532 nm excitation light source, (b) hBN under the 633 nm excitation light source, (c)diamond under the 532 nm excitation light source, (d)diamond under the 633 nm excitation light source.The temperature in the picture is from a thermocouple experiment.The thermocouple temperatures below 800 K are obtained through resistance heating,while those above 800 K are by laser heating.

Figure 5(a)highlights the relationship between the intensity ratio of the anti-Stokes line to the Stokes line as a function of temperature.The intensity ratio of anti-Stokes to Stokes Raman scattering exhibits a significant enhancement with the increase of the temperature, satisfying the Boltzmann distribution law,but without agreement with Eq.(1).To ensure the accuracy of temperature determination by anti-Stokes/Stokes Raman scattering intensities, the thermocouples were used to scale the anti-Stokes/Stokes temperature up to 1500 K,meanwhile the system coupling parameter was also corrected according to the following equation:

where the correction factorγis an indispensable coupling parameter,which includes terms due to the spectrometer settings,the photomultiplier response,quantum efficiency of CCD,and other optics.[17]Thermocouple readings were employed for temperature calibration, while differentγvalues of diamond under 532 nm and 633 nm excitation laser at 800 K were identified, namely,γ532=0.64 andγ633=1.74.The modified Eq.(2)curve is in good agreement with the intensity ratio as a function of temperature, as shown in Fig.5(a).Theγvalues of diamond, hBN, Si, LiGaO2, LiAlO2and SiC were measured by using two excitation light sources.Theγvalues of the same sample remained constant, a typical example of hBN and diamond under 532 nm excitation light source in Fig.5(b).Theγvalue is affected by the Raman modeνof the sample,and the fluctuation range of theγvalue corresponding to the closeνis similar, such asγ=1.26 (E(3), 508 cm-1)andγ=1.34(E(4),613 cm-1)ofγ-LiAlO2under the 633 nm excitation light source.Theγvalues of the same sample at different temperatures of the fixed optical system were averaged and used as the correction factor of the measurement system.

The result shows that, after adjusting a fixedγvalue in the case of the different excited light wavelength, a large deviation between the temperature measured by the thermocouple and the calculated value in Eq.(1)always exist,especially above～700 K.Therefore, the presented formula is not accurate enough to calibrate the sample temperature.In order to address this issue, a detailed study onγfor hBN was carried out at the 532 nm excitation wavelength.Interestingly,we found that the differentγvalues can be probed in theTrange below and aboveT～700 K,withγbeing～0.67 within 300–700 K and～0.86 withinT～700–1500 K.The thermocouple temperature and anti-Stokes/Stokes temperature exhibit a good fitting, as shown in Figs.5(c) and 5(d).After selecting the appropriateγvalue, the difference between the thermocouple thermometer measurement and Stokes temperature measurement results is greatly reduced.The fitting results show that the ΔTmax=46.5 K within 1000 K,ΔTmax=80.6 K above 1000 K,so the error range is±50 K within 1000 K,and±100 K above 1000 K.The error increases because the laser hot spot is much smaller than the thermocouple junction.

The system was calibrated under atmospheric pressure.The correction factorγis affected by the wavelength of the excitation light source, Raman peak position of the sample and other factors,but not by heating methods such as resistance or laser.Theγvaries slightly in the higher temperature region due to the heating of the system.The calibrated thermometry formula Eq.(2) was applied in the high-pressure experiment, as a technology to compensate for the spectroradiometry method within 1000 K and the thermocouple non-in-situthermometry.

6.The application in LHDAC

The anti-Stokes/Stokes thermometry was then applied to the LHDAC experiments with the corrected Eq.(2).The sample was loaded into the DAC chamber, with the upper and lower parts of the chamber being covered with a NaCl insulation layer.The sample was heated by a 1064 nm laser incident from the bottom of the DAC, and the Raman scattering experiment was performed by using a 532 nm/633 nm laser incident from the upper part of the DAC.Raman spectra of samples and diamonds were measured,and temperatures were measured based on anti-Stokes/Stokes Raman line intensities separately.

Figure 6(a) shows the temperature-dependent anti-Stokes/Stokes Raman spectra of hBN and an anvil diamond in a typical LHDAC experiment at 0.7 GPa under 532 nm excitation light.In a high-pressure experiment, the anti-Stokes signal is very weak due to the influence of the sample size;50 times amplification was adopted to highlight the signal changes.With the increase of the temperature parameter, the anti-Stokes signal background increased.Further, the anti-Stokes intensity of hBN and diamond increased significantly,but the Stokes intensity decreased.At the same time,the corresponding temperature was obtained by the intensity ratio.It was found that the diamond was always maintained within 500 K when the sample temperature increased,indicating that the assembly had a good heat transfer and insulation efficiency.

Fig.6.(a)The anti-Stokes/Stokes Raman spectra of hBN sample and anvil diamond in a typical LHDAC experiment at 0.7 GPa under 532 nm,blue circles represent hBN signals and red stars represent diamond signals.(b)Anti-Stokes/Stokes temperature measurement result of the hBN sample and the anvil.The inset in(b)is a schematic diagram of the LHDAC experiment,showing the hBN and diamond measuring points.

7.Anharmonic effect of high-temperature phonon

Based on anti-Stokes/Stokes thermometry, the anharmonic effect of hBN at high temperature and high pressure was also investigated.Perturbation theory is usually used to describe the complex phonon self-energy Δ(ω)+iΓ(ω) to reveal the coupling of harmonic eigenstates by anharmonic interactions.[23]The imaginary part of phonon self-energy explains the phonon life-finalization caused by the decay of the disharmonic phonon,which leads to the broadening of the Raman line shape.There is an energy–time uncertainty relationship between the linewidth of the Raman line and the phonon lifetime,and the information of the phonon anharmonic effect can be obtained through its temperature dependence.[24]

A set of Raman spectra of themode obtained at 0 GPa and different temperatures between 300 K and 1400 K was shown in Figs.4(a) and 4(b).As the temperature increases,the intensity of anti-Stokes increases significantly and the intensity of Stokes decreases.At the same time, the frequency of Stokes Raman peak decreases and the linewidth increases with the temperature shown in Figs.7(a)and 7(b),the fitting parameters are given below and describe the temperature dependence of FWHM (Γ) and Raman shift (υ) of hBN at 0 GPa.The trend is consistent with that reported in previous research.[28]

The linewidth of hBN in this study at 0 GPa is higher than that reported in previous studies,indicating the different crystallinity of the samples.The FWHM increases with temperature, and the nonlinear temperature-dependent combination is attributed to four-phonon decay processes.The calculation shows that with the increase of temperature,the lattice thermal expansion results in the blue shift of themode peak,and the negative peak shift caused by the strong anharmonic effect of the first-order four-phonon scattering progress reverses the influence of the lattice thermal expansion, leading to the significant negative frequency shift with the increase of temperature in the actual Raman spectrum.[25]The Raman frequency and FWHW of hBN in this work.

Figures 7(c) and 7(d) reveal anomalies in the FWHM of hBN under high pressure.Specifically, the FWHM above 400 K decreased remarkably with increasing temperature within 3 GPa,and the FWHM at above 3 GPa raised with temperature and exhibited a higher temperature rate than at 0 GPa.Concurrently,the Raman shift near 4 GPa displayed an inverse correlation with temperature change.The typical Stokes Raman spectra of hBN at 0.7 GPa and 7 GPa are displayed in Figs.8(a)and 8(b),respectively.Figures 8(c)and 8(d)reveal that the temperature coefficient of Raman frequency progressively rises with increasing pressure,shifting from a negative to a positive value.Notably, the pressure range between 3–4 GPa is a crucial transitional interval, as evidenced by the FWHM and peak position of hBN at pressures near 3 GPa exhibiting a similar behavior.Consequently,the primary mechanism that affects broadening and frequency shift within hBN changes near 3 GPa.

From the inset in Fig.8(d), the potential energy curve is found to exhibit a parabolic trend,and the equilibrium positionr0is symmetric in the harmonic approximation.The anharmonic effects of lattice vibration at high temperatures,such as thermal expansion,heat conduction and phonon coupling,cannot be ignored.Under anharmonic effects,the repulsive force between atoms increases, the attractive force decreases, and the potential energy curve is asymmetric.Under high pressure, the repulsive force and attractive force increase at the same time,the asymmetry of the potential energy curve intensifies,and the phonon frequency hardens with the increase of pressure.[29]

In this paper, it is concluded that the strong anharmonic effect caused by the first-order, four-phonon scattering term of hBN at low pressure is significantly dominant and the frequency is subjected to softening as temperature increases.Under high pressure, the degree of molecular localization increases,the effect of lattice thermal expansion on frequency is better than that of a strong anharmonic effect,and the phonon frequency hardens as the temperature increases.

8.Conclusion

In conclusion, we presented an innovative systematic study on the anti-Stokes/Stokes thermometry and the factors affecting the system correction factorsγ,and applied the calibrated anti-Stokes/Stokes thermometry to the LHDAC experiment for hBN anharmonic study under high temperature and high pressure.Anti-Stokes/Stokes thermometry,based on the strength ratio of the anti-Stokes to Stokes lines, measured by Raman spectroscopy,was employed to obtain thein-situtemperature of the sample and diamond anvil,with calibration performed up to 1500 K (±50 K within 1000 K,±100 K above 1000 K).Two excitation laser sources and six samples were employed for the temperature calibration.It is found that the correction factorγof the system is affected by the excitation light source strongly, and is slightly temperature-dependent.The anti-Stokes/Stokes thermometry was further used in highpressure experiments for the study of the anharmonic effect of hBN under HPHT.It is found that the strong anharmonic effect caused by phonon scattering at low pressure leads to the softening of frequency as temperature increases.Under high pressure,the interatomic attraction and repulsive force increase in the local molecular area, the influence of lattice thermal expansion on frequency is dominant;and the phonon frequency hardens as the temperature increases.

Acknowledgements

We thank Prof.Filippo for helpful discussions.This work was financially supported by the National Natural Science Foundation of China(Grant No.U2030107)and the Fundamental Research Funds for the Central Universities (Grant No.2020SCUNL107).