Theory of complex-coordinate transformation acoustics for non-Hermitian metamaterials

Hao-Xiang Li(李澔翔), Yang Tan(谭杨), Jing Yang(杨京), and Bin Liang(梁彬)

Collaborative Innovation Center of Advanced Microstructures and Key Laboratory of Modern Acoustics,MOE,Institute of Acoustics,Department of Physics,Nanjing University,Nanjing 210093,China

Keywords: complex-coordinate transformation acoustics,acoustic non-Hermitian metamaterials,exceptional points,acoustic coherent perfect absorber and equivalent laser

1.Introduction

Transformation acoustics, which is developed from transformation optics[1–5]and direct current conductivity equations,[6]has been studied extensively in the past decade.By establishing a correspondence between material parameters and coordinate transformations, transformation acoustics provides an effective method for designing new acoustic devices.[7–9]One of the most famous and intriguing devices is the invisibility cloak,[10–18]which is able to eliminate reflected sound waves but inevitably results in inhomogeneous and anisotropic parameters inside the cloaking shell.In order to solve the problem that the signals from the outside environment cannot reach the interior of the cloaked domain,a cloaking mechanism has been proposed, which maps the cloaked object to main body of the host material and the cloaking shell only consists of complementary medium made of a singlenegative material, so that the parameters are independent of the host material and communication with the outside world is allowed.[19]Despite the fact that transformation acoustics with real mapping functions has proven effective in steering the trajectory of acoustic waves,it still cannot manipulate the field amplitude in prescribed ways, limiting its applications for designing non-Hermitian devices with complex material parameters in nonconservative systems.

Non-Hermitian physics can be verified by using acoustics and electromagnetics, which not only provide a better understanding[20–22]but also bring non-Hermitian physics closer to practical applications.[23,24]Several interesting researches have shown unique features of exceptional point and exceptional ring[25,26]and the extraordinary capabilities in manipulating wavefronts asymmetrically.[27–29]Recent explorations of loss and gain within the framework of non-Hermitian systems play important roles in controlling acoustic transport, especially amplitude modulation.[8,30–33]In non-Hermitian physics,PT-symmetric system with complex refractive index profilen(-r)=n*(r) is an intriguing branch, whose Hamiltonian commutes with thePToperator, demonstrating remarkable physical properties.[34–46]Recently,as another striking property of non-Hermitian systems,APTsymmetry has been proved, defined by{PT,H}=0,which may facilitate the experiments since it requires either gain or loss.[47–49]With the help of the positive and negative refractive index materials, many intriguing effects can beachieved,such as chiral mode transfer,[50]quantum squeezing and sensing,[51]and shift of EPs.[52]However, the artificial modulation of the imaginary part of wave vector in non-conservative systems, which is crucial for the amplification and attenuation of acoustic waves and the design of non-Hermitian acoustic metamaterials,would require the transformation acoustic method to adapt to complex spatial coordinate space and map complex coordinates.

Here we show that the theoretical framework of transformation acoustics can be extended through the use of complex mapping functions.We derive the theory of complexcoordinate transformation acoustics,and demonstrate how the transformation acoustics is directly related to engineering of non-Hermitian medium, which provides additional degree of freedom to modulate the amplitude and propagation direction of sound waves simultaneously.To the best of our knowledge,no complex-coordinate transformation has been explored in acoustic systems.Specifically, by artificially designing the constitutive parameters of the transfer matrix, we derive the relation between the transmitted and reflected waves and realize the flexible control of EPs in the one-dimensional layeredPT/APT-symmetric structure and investigate the phase transition process in the parameter space.We can also observe the coherent perfect absorber (CPA) and lasing mode in thePT/APTmetamaterials when modulating the constitutive parameters of the Jacobian matrix.A non-Hermitian material can be constructed by using our theory, extending the scope of application for transformation acoustics.Furthermore,it can reduce the complexity of material parameters in comparison with traditional realcoordinate transformation,which may inspire the experimental implementation of a perfect cloak which has not been realized before.[33,50]

2.Jacobian matrix for PT and APT symmetries

Now, we start from the acoustic wave equation with Cartesian coordinatesr=(x,y,z)in the time harmonic form

whereρis the density tensor,κis the bulk modulus, andωis the angular frequency.Analogously to the invariance of the conductivity equation, we map each point in the original space to another space based on a coordinate transformation withp[r′(r)]=p(r).The acoustic equation in the new space becomes

where

which has been proved theoretically in Appendix C.As a result of our proposed theoretical framework of CCTA,by combining Eqs.(3)–(5), we can generate systematicPTandAPTmetamaterials and explain their acoustic properties in terms of analytically continued complex coordinates in the auxiliary free space.For simplicity but without loss of generality,here we consider a one-dimensional (1D) scenario illustrated in Fig.1,which features a slab-type configuration placed in air(ρ0=1.21 kg/m3,κ0=1.42×105Pa), corresponding to the coordinate transformation

with the identity transformation implicitly assumed for|x|＞d(i.e.outside the slab region),dis the thickness of the loss and gain medium,which is set to 2λ.

3.Derivation of scattering matrix

We first use the CCTA method to derive the scattering matrixSof the 1DPT-symmetric structure in Fig.1(b).The corresponding Jacobian matrix can be written as

with the overdot denoting differentiation with respect to the argument.ThePT-symmetry condition requires

which has been proved theoretically in Appendix C.For simplicity, here we consider a coordinate transformation of discontinuous functions

which yields aPT-metamaterial slab.As plane harmonic acoustic waves propagate uponPT-symmetric structures,the background pressure field(p)can be expressed as

wherek0is the wave number for the background medium,A,B,C, andDare the amplitudes of the forward and backward propagating waves in the left and the right background mediums, respectively.The time-harmonic [exp(iωt)] is omitted here for convenience.According to it, we use a transfer matrix to describe the relation between the acoustic waves in the left background medium and right background medium as

By enforcing

the transfer matrixMPTcan be deduced, which is shown in Appendix D.WhenD=0 orA=0 is imposed on the boundary condition for single left or right incidence, the complex transmission(tLortR)and reflection(rLorrR)coefficients of thePT-symmetric structure can be expressed in terms of the components of the transfer matrixMPTas follows:

whereγ=2αk0dandδ=2βk0d.And the scattering matrix can be written as

It is not difficult to find that the transmission coefficient and reflection coefficient satisfy the relation (see Appendix D for the derivation of transfer matrix)

which is the generalized energy-conservation relation in thePT-symmetric structure.[6]

Furthermore,by changing the form of the Jacobian matrix as follows:

we can achieve the requirement in Eq.(5)and realize theAPTmetamaterials.The transmission coefficient and reflection coefficient of theAPTsymmetric structure can be deduced and expressed as (see Appendix D for the derivation of transfer matrixMAPT)

whereγ=2αk0dandδ=2βk0d.It is not difficult to find the relation between the elementary components Im(t)=0, andrL=r*Rdemonstrating that our proposed method can be utilized to realize the acousticAPTmetamaterials,whose concept has been extended to acoustics recently.[53]

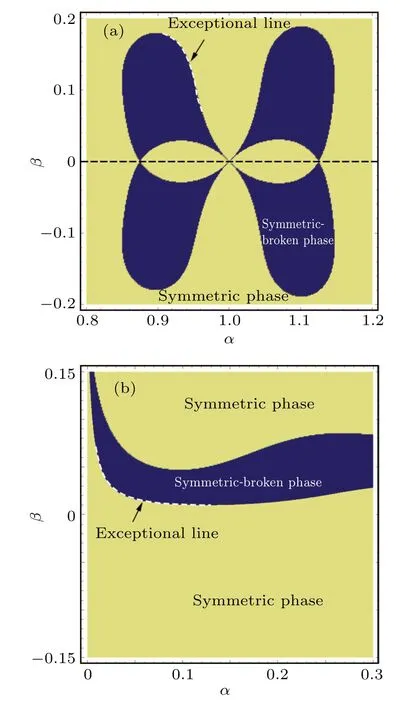
Fig.2.Phase diagram of scattering matrix of (a) 1D PT-symmetric structure and (b) 1D APT-symmetric structure, with yellow (blue)region corresponding to the symmetric scattering phase (symmetrybroken phase),and boundaries between the two regions indicating phase transition marked by white dashed line.

In order to describe the relation between the scattering phase and transformation parameters, we further investigate the phase transition process of the scattering matrix of the 1DPT/APT-symmetric structures in theα–βparameter space,as shown in Figs.2(a) and 2(b).The yellow region corresponds to the symmetric scattering phase, while the blue region corresponds to the symmetry-broken phase.The boundaries between the two regions indicate the phase transition.By changing the value ofαandβ, the constitutive parameters of Jacobian matrix can be further modulated, showing the phase transition point(EP),at which some unique scattering characteristics such as asymmetric reflection can be observed.Furthermore, we can find that the phase diagram of the scattering matrix in thePT-symmetric structure is symmetric with respect toβ=0, which originates from the conjugate symmetric relation between the loss and gain.While in theAPT-symmetric structure,the symmetric-broken phase is sandwiched between two symmetric phases,which means that the scattering matrix can undergo two phase transmissions if we increase the value ofβwith a fixedα.

4.Applications

4.1.Modulation of EPs in metamaterial slab via CCTA method

Here we demonstrate theoretically that EPs in thePTandAPTsymmetric systems, which result in a spontaneous phase transition from symmetric phase to symmetry-broken phase,both can be formed at an arbitrary frequency in our designed slab via the CCTA method.To demonstrate the unidirectional reflection at the EPs, we first consider an isotropicPT-metamaterial slab with a thickness ofd= 2λ, excited by a plane wave.As an example, we set the operation frequencyf0= 3430 Hz, and enforceu0=v0w0=α+iβ=0.951+0.115i andw0=1.Hence the density tensor and bulk modulus can be written as

The observation of EPs in theAPT-symmetric medium is also plotted in Figs.4(a)–4(d).The two eigenvalues and eigenvectors can be written as[54]Whent ＞Im(rL), the two eigenvaluesλ±are both real and the absolute value of the second component of the eigenvectors|Ψ2| is 1, which corresponds to theAPT-symmetric phase.The other phase,where the two eigenvalues are conjugated,is referred to as theAPT-broken phase.In the simulation,by selecting appropriate constitutive parameters one hast=Im(rL),which is referred to as an EP,and a spontaneous phase transition occurs, for both the eigenvalues and eigenvectors of the scattering matrix can be observed at 3430 Hz(see Appendix E for the asymmetric reflection in theAPT-symmetric structure).

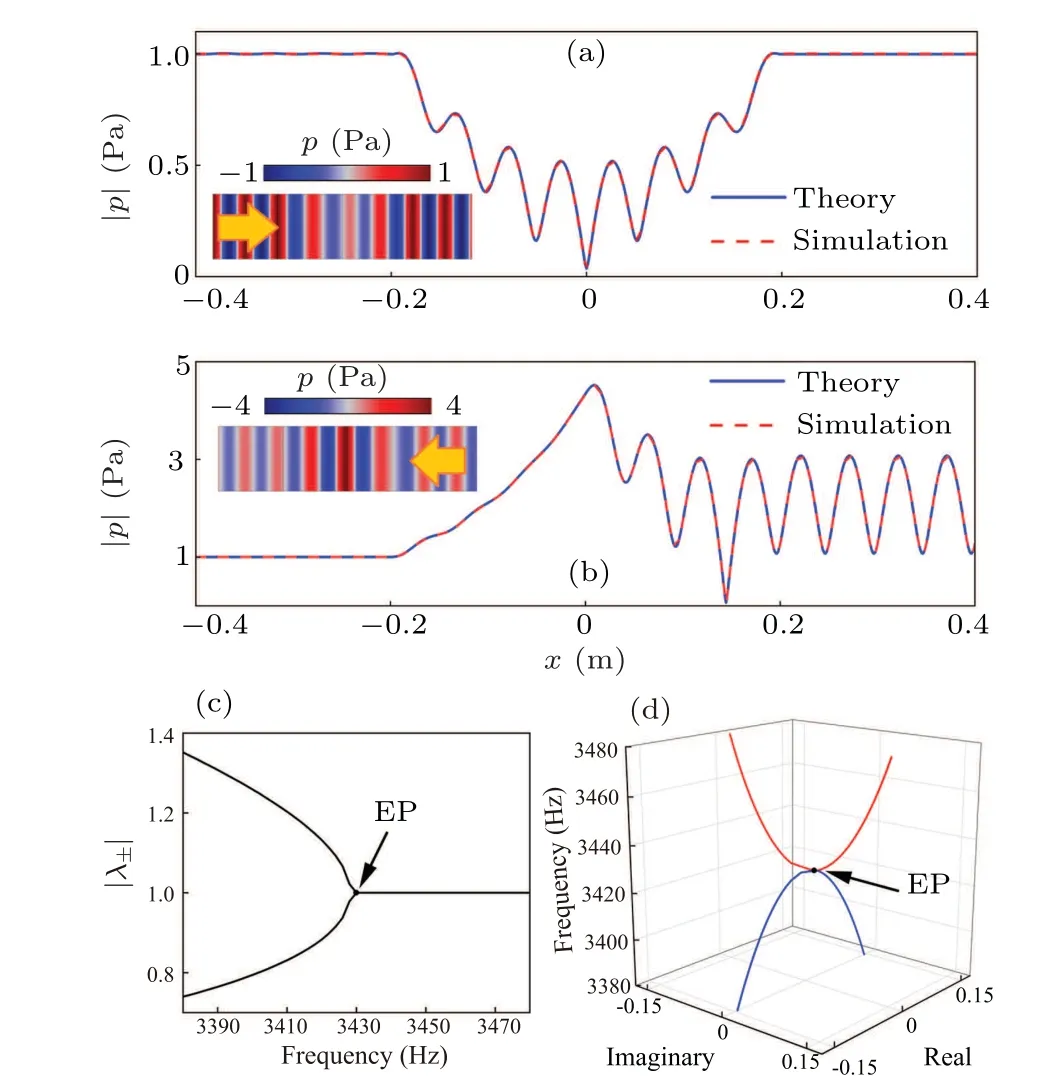
Fig.3.EPs in PT-symmetric structure, showing simulated pressure amplitude distributions of the PT-symmetric structure under (a) the left incidence and (b) the right incidence with constitutive parameters u0 =v0w0 =α+iβ =0.951+0.115i and w0 =1, with inset showing pressure field distributions, and absolute values of(c)eigenvalues and (d)the second component of eigenvector of corresponding scattering matrix rL/rR for this acoustic PT-symmetric medium, with eigenvectors normalized such that the first component is always unity.

Fig.4.EPs in APT-symmetric structure, showing simulated pressure amplitude distributions of the APT-symmetric structure under(a)the left and(b) the right incidence with constitutive parameters u0 =v0w0 =α+iβ =0.458+0.095i and w0=1,with insets showing pressure field distributions,and (c) imaginary part of the eigenvalues and (d) absolute value of the second component of the eigenvectors for this APT-symmetric medium,with eigenvectors normalized such that the first component is always unity.

4.2.CPA and laser effect via CCTA method

A 1DPT-symmetric structure can act as a CPA and threshold laser simultaneously.In the following, we use the CCTA approach to realize this distinctive property by selecting theu,v,andwvalues in Eq.(9).

In an acoustic CPA-lasing mode,the elementary components of the transfer matrix need to satisfy

which means a zero and a pole of theSmatrix coincide at a real frequency simultaneously.[46,55,56]Consideringt=1/M2,2≫1,the system is in thePT-broken phase,[33]whose eigenvaluessaandsbare nonunimodular and= 1.When two counter propagating coherent waves are incident in the form of two eigenstates,one with an eigenvalue(sa=0)will be fully absorbed, indicating a CPA, while the other (sb=1/sa=∞)will make the acoustic system emit outgoing amplified waves,indicating threshold lasing.[57]

We simulate an example to achieve CPA-lasing mode by settingd=2λ=0.2 m,f0=3430 Hz,α=1.328, andβ= 0.159 (i.e.,v0w0=u0= 1.328-0.159i andw0= 1),which enables a zero and a pole of theSmatrix to coincide at 3430 Hz,as shown in Fig.5(c).Here we use the output coefficient as a key parameter(Θ)for defining the ratio of total outgoing acoustic intensity to the total incoming intensity[58]

whereIL,IR,OL, andORrepresent the input intensity and the output intensity on each side of the structure,respectively.By adjusting the phase offset between two incident waves to-π/2, a sharp absorption dip ofΘdown to-37 dB can be observed near the operation frequency 3430 Hz (blue dotted line), which corresponds to the perfect absorption of sound waves(Fig.5(a)).Meanwhile,with the phase offset switched toπ/2, it is the lasing mode that the power flows are completely reversed and the amplitudes of the outgoing waves are found to be nearly 180 times that of the incident waves(Fig.5(b)), with a maximum amplifiedΘof 45 dB near the same wavelength (red dotted line).We search for the conditions thatΘreaches minimum and maximum,which indicates that the output signal is completely absorbed and significantly amplified, corresponding to the CPA and lasing mode.The contrast ratioQbetween theΘunder two incident conditions can be expressed as[59]

which shows that the highest intensity contrast peak appears at 3430 Hz(black solid line)in Fig.5(c).

Fig.5.Acoustic CPA-lasing mode achieved in PT-symmetric structure via CCTA method,showing pressure amplitude distribution of structure in(a)CPA mode,(b)lasing mode under incidence of two-port coherent waves with the relation D=(∓6.352i)A,with inserts showing simulated pressure field distributions, with parameters being d=0.2 m, f0 =3430 Hz, α =1.328, and β =0.159, and(c)spectrum output coefficient Θ =(OL+OR)/(IL+IR) of the CPA-laser at frequency ranging from 3420 Hz to 3440 Hz, with blue, red, and black lines representing the output coefficient of CPA,laser,and the contrast ratio between maximum value and minimum value,respectively.

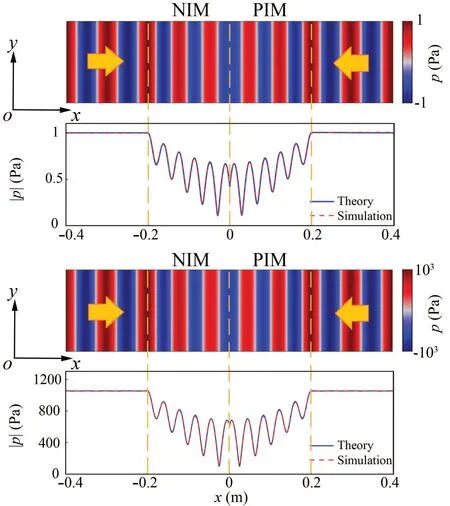
Fig.6.(a) Acoustic CPA mode and (b) lasing mode achieved in APTsymmetric structure via our proposed CCTA method, with simulated pressure field distributions (upper panels) and pressure amplitude distributions(lower panels) of the structure, under the incidence of two-port coherent waves with the constitutive parameters:u0=1.328-0.075i and u0=v0w0=1.296+0.078i,demonstrating the CPA and lasing effect where two incident waves are significantly absorbed and amplified,and vertical dashed lines referring to the boundaries between the NIM,PIM,and background medium.

Moreover, the CCTA method we proposed in this work can also realize the CPA and laser mode in theAPTmetamaterials.In an acoustic CPA mode,the two outgoing waves will disappear,i.e.,A=D=0.Based on Eq.(11),the condition of achieving CPA can be written as

We demonstrate a typical example of the CPA effect and plot the simulated results in Fig.6(a).Withd= 0.2 m,f=3430 Hz,the conditionM1,1=0 can be achieved by choosing the constitutive parameters asu0=v0w0=1.328-0.075i andw0=1.Therefore, in the simulation, the two incident waves will be completely absorbed if they conform to the relation:D=(0.983+0.211i)A.Meanwhile, we find that the spatial derivation of the pressure field changes abruptly at the boundaries of the positive index material (PIM) and negative index material (NIM) despite the pressure field being still continuous at the boundaries,owing to the opposite sign of the mass densities of the PIM and NIM.In addition,if

the transmission coefficient approaches infinity, corresponding to the lasing mode.In the simulation,we setu0=1.296+0.078i to satisfy the relation in Eq.(24).Figure 6(b) reveals that sound waves are amplified 1000 times under two incident waves with amplitudesA=D.

5.Conclusions

In this work, we drive the theory of the complexcoordinate transformation acoustics and show that such a method can be used to design non-Hermitian acoustic materials, such asPT-metamaterials, modulating both the phase and amplitude of the acoustic field.Moreover,we demonstrate this idea in the one-dimensionalAPT-symmetric structure and observe the spontaneous phase transition of the scattering matrix in the transformation parameter space, which has not been discussed before.The first example demonstrates that the EPs can be modulated in theAPT-symmetric structure by modulating the Jacobian matrix’s constitutive parameters.In addition, the poles and the zeros of the scattering matrix can also be obtained forAPT-symmetric system to act as both a coherent perfect absorber and a laser.This transformation theory provides another aspect for us to design acoustic functional devices, which is expected to explore more fascinating non-Hermitian phenomena such as asymmetric absorbing,[60,61]amplifying,[62]and sensing.[63]

Appendix A:Pseudo-Hamiltonian formulation

In order to derive the general relation of material parameters in thePT/APTmetamaterials, we refer to the optical systems and consider the time-harmonic, sourceless acoustic equation pertaining to an anisotropic and inhomogeneous background described by the density tensor,bulk modulusκ(r)and time variation[exp(iωt)]

Using a method similar to that in Ref.[45] we can convert Eq.(A1) into an eigenproblem in a compact operator form,specifically,

with

Appendix B: Commutation of PT/APT and pseudo-Hamiltonian operators

Since the system satisfies thePTsymmetry condition and the operatorℒplays a role of a pseudo-Hamiltonian,i.e.,

We can achieve[recalling that(PT)2=1]

Substituting Eq.(A4) into Eq.(B2) and considering the restraint condition:PT(iΩ)=iΩandPT(i∇)=i∇,the material parameters should satisfy

which is the distribution condition of the refractive index underPTsymmetry.[64]

And if the acoustic system is under theAPT-symmetry condition,i.e.,

using the method similar to that for Eqs.(B2) and (B3), we can find the antisymmetric refractive index and mass density as follows:

Referring to the literature related to acousticAPTsymmetry,[64]we obtain the more generalized distribution characteristics of material parameters.

Appendix C: Relation among constitutive parameters for PT/APT symmetry

We first derive the relation among constitutive parameters for the 1DPTmetamaterial in Fig.1(b).Substituting Eq.(7)into Eq.(3), we obtain the transformed material density and bulk modulus of elasticity,which are given below:

where

Considering that the material parameters in thePT-symmetric structure should satisfy the relation in Eq.(B3), the constitutive parameters are required to meet the following condition:

As reported in the main text,if the constitutive parameters satisfy Eq.(C3),the corresponding Jacobian matrix will automatically fulfill the relation in Eq.(4).And since we consider a coordinate transformation of discontinuous functions expressed in Eq.(9),the Jacobian matrix and material parameters should satisfy the relation

which clearly shows that the transformed material parameters satisfy thePT-symmetry condition.

As for theAPT-symmetric structure in Fig.1(c),we consider a coordinate transformation of discontinuous functions

And the relations of the Jacobian matrix and material parameters can be given by

Appendix D:Derivation of transfer matrix M

As shown in Fig.D1,a 1D acousticPT-symmetric structure consisting of two layers of media,is immersed in a background medium with a density ofρ0and a velocity ofc0.The total field within each medium be regarded as a superposition of forward and backward propagating wave.At the boundaryx=-d,the pressure fields(p),which are on both sides of the boundary,can be written as

wherek0is the wave number for the background medium,A,B,E, andFare the amplitudes of the forward and backward propagating waves in the background and the loss medium,respectively.

Consider that the transformation relation between the sound pressure and vibration velocity at the boundary satisfies[9]

whereAis the Jacobian matrix of the transformation.We derive the transfer matrix at the boundaryx=-das given below:

According to the Refs.[53,54,65], the transfer matrix on the left-hand side can be expressed as

The transfer matrixM=finally reads

Letu0=α+iβ, andv0w0=u0, then the four elementary components(M1,1,M1,2,M2,1,andM2,2)of the transfer matrixMPTwill be able to be simplified into the explicit expressions

whereγ= 2αk0dandδ= 2βk0d.By simplifying the formula above, we can find that the elementary components of the transfer matrix satisfy the relationM2,2=M*1,1,M1,2=-M*1,2,M2,1=-M*2,1, which has been verified in the literature.[44,45,66]

As for theAPT-symmetric structure, the transfer matrix can be calculated in a similar way as the above-mentionedPT-symmetric structure,while the difference is that considering theAPT-symmetry relationship(Eq.(C6)),a pair of positive index material(PIM)and negative index material(NIM)needs immersing in air.The transfer matrixMAPTcan be written as

By settingu0=α+iβ,v0w0=u0,the four elementary components(M1,1,M1,2,M2,1,andM2,2)can be simplified into

from which we can figure out the relation of the elementary components Im(M1,1)=Im(M2,2)=0 andM1,2=-M*2,1in theAPT-symmetric structures.

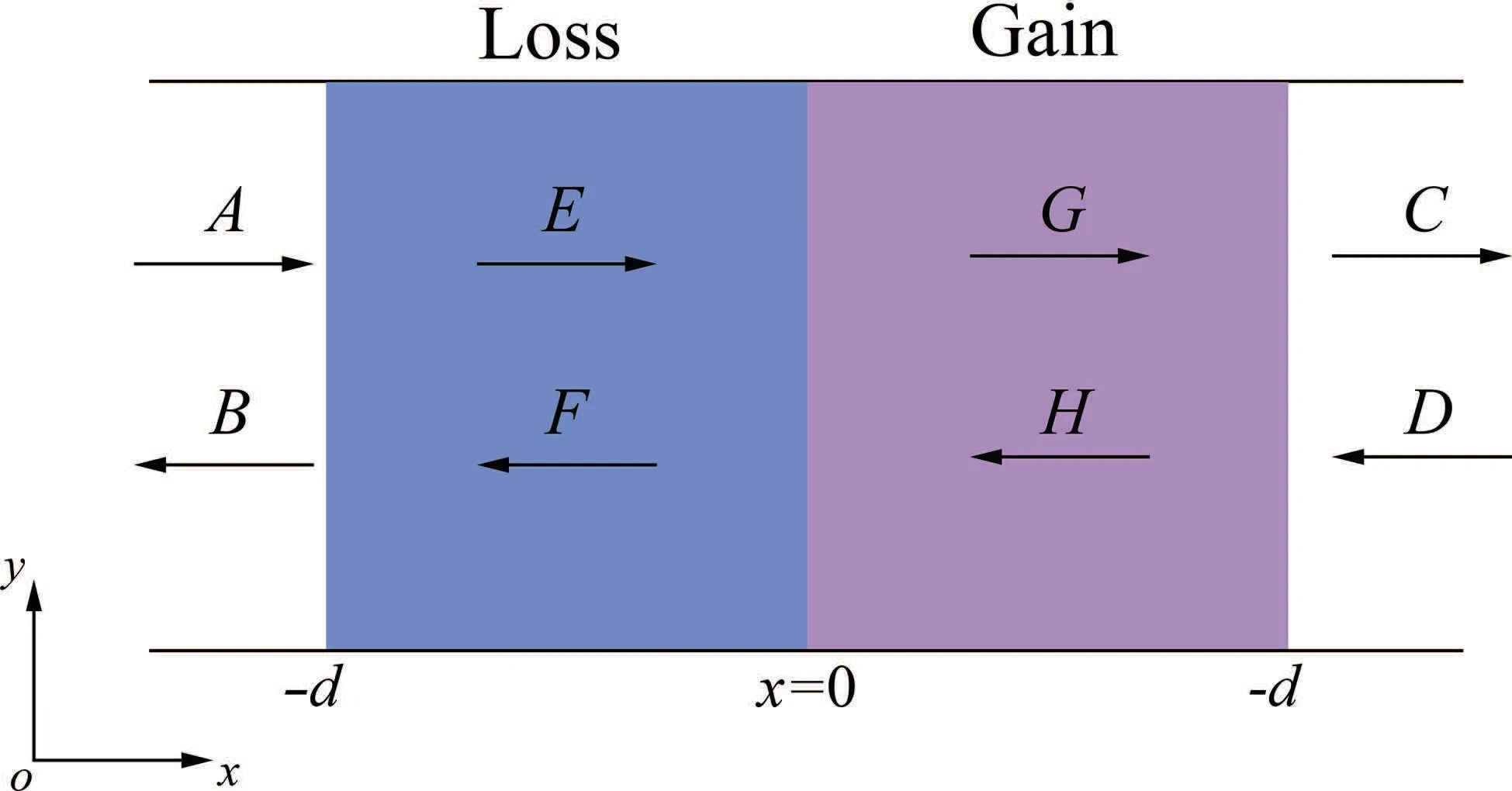
Fig.D1.Schematic diagram of 1D acoustic PT-symmetric structure,consisting of a pair of loss and gain medium with the same width d immersed in a passive background medium(the leftmost and rightmost regions),with black lines indicating hard walls of structure.

Appendix E: Asymmetric reflection in APTsymmetric structure

In theAPT-symmetric optical structure, the reflection coefficient and transmission coefficient satisfy the relation[53]

According to Ref.[54], at the phase transition point, no particular property is found for the reflection coefficient and transmission coefficient, which makes it hard to judge whether the system is at the exact EP from Figs.4(a)and 4(b).In order to further demonstrate this property, we depict the phase distribution at the upper boundary of theAPT-symmetric structure in Figs.E1(a) and E1(b), which shows a notable difference when the acoustic wave is incident from the left side and the right side,respectively.Furthermore, we calculate the reflection coefficient and transmission coefficient in Figs.4(a) and 4(b) as given below:

Fig.E1.Asymmetric reflection in APT-symmetric structure.Simulated pressure field distributions (upper panels) and pressure amplitude distributions (lower panels) at the upper boundary of the APTsymmetric structure under (a) left incidence and (b) right incidence,respectively,with constitutive parameters being u0=v0w0=α+iβ =0.458+0.095i,and vertical dashed lines indicating boundaries between the NIM,PIM,and background medium.

which satisfy the relationt=±Im(rL)at EPs,demonstrating that theAPT-symmetric structure can be modulated at the phase transition point by our complex-coordinate transformation method.

Acknowledgements

Project supported by the National Key Research and Development Program of China(Grant No.2022YFA1404402),the National Natural Science Foundation of China (Grant Nos.12174190, 11634006, 12074286, and 81127901), the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures,and the the Priority Academic Program Development of Jiangsu Higher Education Institutions.