Classification and structural characteristics of amorphous materials based on interpretable deep learning

Jiamei Cui(崔佳梅), Yunjie Li(李韵洁), Cai Zhao(赵偲), and Wen Zheng(郑文),2,†

1Institute of Public Safety and Big Data,College of Data Science,Taiyuan University of Technology,Jinzhong 030600,China

2Shanxi Engineering Research Center for Intelligent Data Assisted Treatment,Changzhi Medical College,Changzhi 046000,China

Keywords: amorphous,interpretable deep learning,image classification,finite scale analysis

1.Introduction

The amorphous matter is a complex multi-body interaction system with long-range disorder and energy metastable for a long time.[1]In the past decades,important new progress and breakthroughs have been made in the frontier fields of amorphous materials, including new materials and new applications,[2–6]which are playing an increasingly important role in high and new technology fields such as energy, information, national defense, and aerospace.The 2021 Nobel Prize in Physics was awarded to Italian scientist George Parisi(G.Parisi),in recognition of his pioneering contribution to understanding complex and disordered physical systems.It also shows the important scientific significance of studying disordered system itself.As a relatively simple disordered system,amorphous materials provide a model system for the study of fundamental problems in physics and material science.The research on it will greatly promote the development of complex disordered system research.

However,the research and application of amorphous materials are also faced with key bottlenecks such as how to improve the formation capacity and room temperature plasticity.Understanding and predicting the ability of amorphous formation is a complex and multifaceted problem.Part of this complexity is due to an inadequate understanding of the amorphous structure.Meanwhile, identifying the structural features and quantifying the structure-property relations of amorphous materials is also a difficult task due to their disorder and complexity.Some structural analysis methods,such as xray diffraction,[7]radial distribution function,[8]and Steinhart bond order parameter,[9]are often used to detect crystal structure in samples or study the order of sample structure.However,these standard techniques have limitations.For example,the accuracy of x-ray diffraction is greatly affected by grain size and texture.The radial distribution function depends on the spatial average and takes a long time to compute.Steinhardt bond order parameters can be hindered by thermal fluctuations or fuzzy crystal structures.At the same time,the traditional analytical methods in the field of amorphous materials have high cost, long cycle time and low efficiency, which makes the analysis of irregular structures challenging.

In recent years, machine learning has made unprecedented advances.Thus, a new machine learning technology,deep learning,has been extended,which has demonstrated excellent capabilities in many fields.[10–13]The research on the interpretation of machine learning has become a hot topic in research conferences in the past two years.[14–17]Because people are not only satisfied with the effect of the model but also think more about the reasons for effect of the model.The new research paradigm of machine learning provides new ways and opportunities to solve the key problems in the field of complex materials.

Now, many scholars have used machine learning methods to analyze or identify the structure of amorphous materials.[18–22]For example, they use neural networks with certain training to classify or predict non-crystalline structures.[23–25]These machine learning methods improved material identification quality and identification efficiency when applied to a variety of complex systems.However, it is very challenging to study the structural characteristics of amorphous systems because they show it a state of long-range disorder, making it difficult to define the structural order parameters.There have also been several recent studies that have successfully used interpretable machine learning approaches to reveal previously unknown relationships between the structure and molecular dynamics of amorphous materials,and they have proposed new order parameters through the learning results of network models.[26–28]

In this work, we took the amorphous model as the research object, and simulated the two-dimensional liquid conformation diagram and amorphous solid conformation diagram based on molecular dynamics as typical examples of amorphous materials.We constructed an interpretable deep learning model that uses Efficient Net to accurately classify amorphous configuration data.The classification effect of this model is better than other image classification networks, and the accuracy is up to 92.75%.We then used Grad-CAM to map the amorphous configuration and explain the important structure of the model to classify the amorphous.We extracted an order parameter from the thermal map.By using this order parameter,we could clearly quantify the structural changes during the transition from a liquid to an amorphous solid,and the order parameter conforms to the physical finite-scale effect.

2.Method

2.1.Simulation details

General liquids form an ordered crystal structure after slow cooling or compression.Some materials may be severely too cold to do not nucleate, or the samples may cool down faster than the nucleation rate.The colloidal glass transition behavior is very similar to this amorphous transition, where the key control parameter is the volume fractionφ(the volume fraction occupied by the solid particles).[29–31]The larger the volume fraction of colloidal suspension,the higher the viscosity, and the system becomes colloidal glass after exceeding a certain concentration.[32]Therefore,we will study amorphous materials by simulating this colloidal glass.

We construct a hard sphere model with periodic boundary conditions to simulate two-position non-crystals.[33]Each system containsN/2 large balls andN/2 small balls,both of their mass arem.Volume particles and boundary particles interact pairwise through the following finite range of pure repulsive potentialV:

whereri,jis the distance between the two particles andσi,jis the sum of the radii of the two particles.α= 2 andα=5/2 correspond to harmonic and Hertzian spring interactions respectively.εis the characteristic energy scale of the interaction.

We ignored the effects of pressure and shear forces on the system during the simulation.We assigned a random initial position to each particle and set the diameter of the large ball to be 1.4 times that of the small ball.We used the FIRE minimization algorithm to record the intrinsic structure energy per particle in the system.The intrinsic structural energy of the configuration is the potential energy that brings it to a local minimum, and it is used to quantify the stability of the configuration.After the simulated evolution, we calculated and recorded the coordinate position of each particle as well as the number of its neighbor particles.We judge whether the system is stable in the simulation process according to its potential energy.When the potential energy is greater than 1×10-16,we output it as stable state configuration data and regarded it as an amorphous solid.When the potential energy is less than 1×10-16,we output it as the configuration data of the unstable state and regarded it as liquid.

The configuration map obtained by directly simulating the model is very difficult to distinguish in the case of human eye observation.In order to facilitate machine learning to better learn the characteristics of the amorphous configuration, we add information about the force in the middle of the particles,that is whenri,j ＜σi,j,a force chain was added between the particles,as shown in Fig.1.Figure 1(a)is a stable configuration,and the system is an amorphous solid;Figures 1(b)–1(d) are shown as unstable configuration diagrams under different volume fractions, and the system is in liquid state.

Fig.1.Amorphous solid configurations and liquid configurations for molecular dynamics simulations.Panel (a) is the stable amorphous solid configuration at φ = 0.838, panel (b) is the unstable liquid configuration at φ =0.838, panel (c) is the unstable liquid configuration at φ =0.832,and panel(d)is the unstable liquid configuration at φ =0.842.

2.2.Construction of the data sets

Our goal is to train deep learning algorithms to perform a binary classification task: to identify whether the configuration map of a particle is an amorphous solid or a liquid.Where amorphous solids and liquids are defined by Subsection 2.1,figure 1 shows several illustrations.We used the data generated from the model simulations in Subsection 21.to constitute the four data sets.We set four systems of different sizes in the data set with particle numbersNof 128,256,512,and 1024,respectively.For each system,we averaged several points within the interval of volume fraction[0.827,0.848]and simulated 1000 data in the environment of each point to form the data sets of four systems.Each of the four data sets is specific to only one particle number amorphous configuration.In order to study the amorphous configuration of the four systems simultaneously,we took an average of 2000 data sets from the four data sets to form the fifth mixed data set.The data set has 104data, and the configuration data of different particle numbers and different volume fractions are distributed in the same proportion.This data set can be trained to directly classify the four systems.We divide the training set and the test set 3:1 for each data set.In this process,we ensure class balance,such as 4000 liquid configurations and 4000 amorphous solid configurations in 8000 data sets with systemN=256.Before model training,the code will label the liquid images as 0 and the amorphous solid images as 1 based on the labels provided by the simulation data.

2.3.Interpretability deep learning model

The interpretable deep learning model we developed consists of two parts: the convolutional neural network EfficientNet classifies amorphous configuration images, and the gradient-weighted activation-like mapping method generates heat maps, as shown in Fig.2.The upper part of the figure shows the structure of EfficientNet.Its input is a noncrystalline configuration image.We propagate the images forward in the model and output the prediction scores of the network for the input conformation images.At this point, we are able to determine the prediction category of EfficientNet for the input configuration image by the prediction score.The bottom right part of the figure shows a simple example of the gradient-weighted class activation mapping method.After we have obtained the predicted scores of the output, we set the gradient of the amorphous solid class to 1 and the gradient of the liquid class to zero, and then backpropagated this signal to the rectified convolution feature map of interest.We combine them to compute a rough Grad-CAM location (thermal map) that represents where the model will make a particular decision.We need to test and select EfficientNet before constructing the model.

Fig.2.The interpretability deep learning model framework.The model consists of an EfficientNet classification network and Grad-CAM, where the EfficientNet is stacked by MBConv modules,the EfficientNet input is the amorphous material configuration,and the output is the predicted score.

2.3.1.EfficientNet

EfficientNet is a convolutional neural network utilizing a multi-dimensional hybrid model scaling approach.[34]The proposed algorithm can not only achieve high accuracy but also fully save the computing power resources.The performance is far better than the various networks in the history of ImageNet, and the has been verified in various applications.[35–38]EfficientNet scales the network width,depth,and resolution,and has 8 structures.We designed a set and test experiments to measure the network accuracy of different structures by their training accuracy and loss value.The comparison results are shown in Table 1, so the EfficientNet-B1 network was selected.

Table 1.EfficientNetB0-B7 network comparison experiment results.

The EfficientNet in our model consists of nine modules.The first module is an ordinary convolutional layer with a core size of (3,3) and a step distance of 2.The 2–8 modules are all repeatedly stacked MBConv structures, while the ninth module consists of an ordinary convolutional layer with size of (1,1), an average pooling layer and a fully connected layer.The MBConv module contains the ordinary convolutional layer,the deep separable convolutional layer(more efficient convolution through depthwise convolution and pointwise convolution), the Swish activation function, and the Dropout layer, and the attention mechanism is embedded in the module(SE block,the network learns the feature weights according to the loss,so that the effective feature map weight is significant).The structure is shown in Fig.2.

2.3.2.Grad-CAM

The gradient-weighted activation-like mapping method(Grad-CAM)is a technical for“visual interpretation”for deep convolutional neural networks.[17]As the depth of the convolutional neural network continues to increase,the system will be able to capture the features of the input image in greater detail.That is,the last layer in a convolutional neural network should have the most detailed recognition of the image features.Whereas in a convolutional network containing a dense layer,the last convolutional layer will spatially expand its activation values,thus losing its spatial information.Thus,Grad-CAM makes use of the gradient information in the last layer of the afferent neural network in order to solve the role of each neuron in classification recognition.

When convolutional neural networks are used for image classification tasks,its final layer is usually the softmax layer,which converts all output values into probabilities.The maximum valueycof the output corresponds to categoryc.We backpropagate on the node with the maximum possible classification type to obtain the gradient of the previous convolutional layer, namely∂yc/∂Aki,j, whereAis the feature map output from the previous convolutional layer,kis the sequence of channel dimensions of that feature map,andiandjare the ordinal numbers of the width and height dimensions respectively.A global averages found in each feature map,i.e.,

Finally,we multiplied the activation value of the last convolution layer with the mean of the previous gradient feature,and then added it up to get a formula for Eq.(3).Among them,the functions of relu function is to maintain a pixel value with a positive effect on the classification,while reducing the pixel value with a negative effect on the classification.We can understand this process as,multiplying the importance of each feature channel by our convolution layer output, which is equivalent to a weighted operation.Ultimately,we obtain a heat map based onH

3.Results and analysis

3.1.Classification results

We used multiple evaluation metrics,such as AUC,Accuracy,Precision,and F1,to fully reflect the classification model performance.The AUC is the area under the ROC of the subject operating the characteristic curve,and the ROC curve characterizes the true positive rate TPR=TP/(TP+FN)and the false positive rate FPR=FP/(FP+TN).TP is true positive, FN is false negative, FP is false positive, TN is true negative.We label liquids as positive and amorphous solids as negative during classification.An AUC of 0.5 means that the performance of the classifier is no better than the random chance level,and 1.0 means perfect classification.The higher the AUC,the better the model is in terms of classification performance.Figure 3 shows the ROC curves and their AUCs of the classification models in this paper and the other three classification models for the test dataset ofN=256.We see that EfficientNet has the largest area under his ROC curve relative to the other models, with an AUC value of 0.953.This intuitively judges that our classification model has relatively high accuracy.However, this kind of result is relatively general,and we cannot judge the effect of the model solely according to AUC.

We continue to use other evaluation metrics to evaluate the results of the different experiments.Accuracy represents the proportion of correctly classified samples to the total sample number.Precision= TP/(TP+FN), indicating accuracy.TPR is also called recall.F1 is the harmonic average of the precision rate and the recall, which is expressed as F1 = 2(Precision× recall)/(Precision + recall).We independently train and test the crystalline configuration dataset of the four systems to calculate the evaluation value based on the prediction scores given by the classification model.

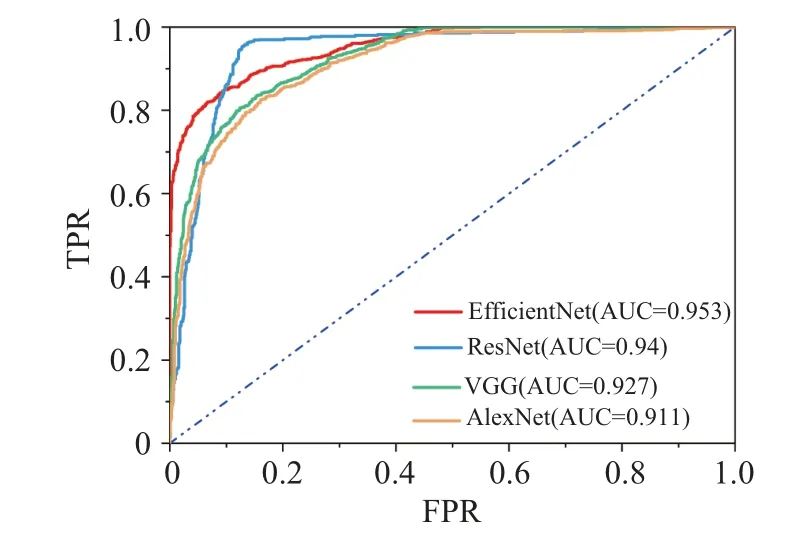
Fig.3.The classification results of EfficientNet with other classification models for non-crystalline configuration data.The curves in the figure are the ROC curves of four models for classification of 2000 test data,red corresponds to EfficientNet,blue corresponds to ResNet,green corresponds to VGG,and orange corresponds to AlexNet.The AUC values were defined as the area under the ROC curve.

Table 2 presents the Precision, Accuracy as well as F1-score of our classification model under different datasets.Four of these datasets have Precision＞81%, indicating that the classification model is very efficient for identifying the class of amorphous.Accuracy is above 87%,and F1 average accuracy and recall is above 86%, which indicates that the model performs well in the classification of the data overall,although the classification accuracy for different categories varies.From the longitudinal comparison, the classification model has the highest classification accuracy on theN=1024 dataset, with F1 reaching 93.15%,and the amorphous materials in large systems are easier to classify compared to the smaller systems.These results show that the EfficientNet classification model enables an accurate classification of liquid versus amorphous solid configurations,without the description parameters of the particle environment in the classification process.Although the structure of the material is only slightly different,we simply need to give the basic geometric information(the particle coordinates and forces presented in the form of images), and the classification model can achieve excellent classification results.

Table 2.EfficientNet compares the experimental results for different datasets.

Next, we compared the classification metrics of the EfficientNet classification model with the results of other image classification networks(the ROC comparison results have been shown in Fig.3).The networks we chose for comparison are AlexNet,[39]VGG,[40]and ResNet[41]networks.These models are convolutional neural networks with different network layer structures and have good performance in previous image classification tasks.To ensure a fair comparison, we trained and tested the different models using the same dataset(N= 1024), and took the average score of the five experiments for each model.Table 3 presents the evaluation metrics for the different models on the systemN=1024.The data demonstrate that our classification model has a relatively optimal classification effect compared to the other networks,with a classification accuracy of 92.75% and an F1 score of 93.15%, which also improves the overall performance of the interpretable deep learning model.

Table 3.Comparing the experimental results between the different classification networks.

Since the EfficientNet classification model can accurately identify liquids and amorphous solids prepared under the same intrinsic structure and environment,it is not a simple calculation of energy as a means of classification.We need to discuss how the model makes classification decisions.In this regard we will use Grad-CAM to provide an interpretation of the model classification results.

3.2.Heat map

We use the Grad-CAM in Subsection 2.3 to generate an activation-like thermal map of the amorphous configuration.The model diagram in Fig.2 shows the process of generating a thermal map.We indicate where the model will make a specific decision on the configuration image by visualizing the spatial gradient of pixels.The thermal map generated by the model will show which part of the picture is activated most by the neural network in the form of weights.Figure 4 shows the visualization results of the Grad-CAM model for two noncrystalline configurations.The liquid configuration is shown on the left and the amorphous solid configuration is shown on the right.The thermal map is similar to an infrared imaging map, with different colors representing the importance of features at that location for classification.In the left panel the model’s interpretation of the liquid highlights two sets of irregular structures, and the interpretation of the amorphous solid in the right panel covers most of the structure.

The above visualization results show that the classification model makes classification decisions on amorphous configurations based on the distribution of these important structures, not relying on the energy calculation of the system,which shows that our deep learning model is an effective tool for identifying amorphous materials.Further, we quantified the visual results to find out the physical properties of the universality.

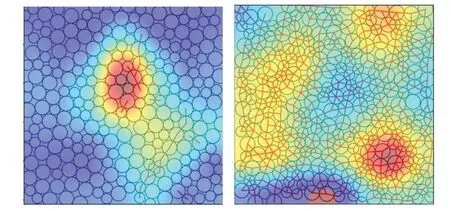
Fig.4.Grad-CAM thermal map visualization of amorphous material configuration.The left map is the heat map of the liquid configuration,and the right picture is the heat map of the amorphous solid configuration.

3.3.Order parameter

Because the coverage of the important regions identified by the DL model is different,we use the sequence parameterhto quantify the important structure identified by the classification model in the configurations,represented by the following formula:

The meaning of the order parameterhis to make a global average over a broad and high dimension of the pixel spatial gradient calculated by the model.The feature parts that have a high weight on the classification decision in the thermal map have a large activation value, so when the area of the red region in a class activation map is more,that is,the distribution of the identified important structures is larger, the value ofhwill be larger.

The scale of the system is usually finite in the simulation,so we do a finite scale analysis of the order parameters.We calculated the order parameter for the data at different volume fractions in different systems,selecting four systems with particle numbers of 128, 256, 512, and 1024.To eliminate the effect of error between the different models produced by the training,first,we use the mixed data from these four systems to train the model derived from the classification network to calculate the order parameters.Second, for each system, we took an average of 11 points in the interval of[0.827,0.848],and took 100 configuration data under the volume fraction of each point, calculated its order parameter and averaged it.After the data is normalized, the order parameter can be expressed ashy=hf(φ,N), whereφis the volume fraction,Nis the number of system particles, andhfis a function of the normalized order parameter under the calculation conditions(φ,N).As shown in Fig.5,the black points and lines are the sequence parameters and their fitting curves for different volume fractions underN=128.Similarly,the points and lines of the same color are the sequence parameter data with the corresponding system sizes.hywill be within a certain range of the volume fraction obvious jump from 0 to 1.Combined with the definition analysis of the order parameter, when the volume fraction of amorphous systemφis less than 0.848 and greater than 0.820,the special structure identified by the model from the amorphous configuration is undergoing complex changes,especially the distribution changes.Whenφ ＜0.820 or whenφ ＞0.848,the state of liquid,as well as amorphous solid,has stabilized.This can also be verified by analyzing the underlying behavior of the non-crystals.Taking the systemN=256 as an example,the left part of the figure is shaded to indicate that 90% of the simulations are liquids, and the right part of the figure is shaded to indicate that 90% of the simulations are amorphous solids.Therefore, we reveal the transformation of liquids to amorphous solids by analyzing the changes of the order parameters.The change rate ofhywill increase as the system becomes larger.For example,whenN=128,hychanges slowly;whenN=1024,hychanges rapidly from 0 to 1.In this case,the system is of finite size and cannot represent the law of the whole ensemble.

Fig.5.The trend of the order parameter hy with volume fraction. hy indicates the proportion of significant regions in the heat map.The blue points in the figure are the ordinal parameters of the system at different volume fractions when the number of particles is 256,and the purple line is the fitted curve to these points.The left part of the figure is shaded to indicate that 90%of the simulations in the N=256 system are liquids,and the right part of the figure is shaded to indicate that 90%of the simulations in the N=256 system are amorphous solids.The horizontal coordinate of the graph is the volume fraction φ and the vertical coordinate represents the ordinal parameter hy.

For amorphous first-order phase transitions,when the order parameter is compared to(φ-)N1/2,we want the order parameter of different system sizesNto collapse into a curve,so the finite-scale scaling behavior of the order parameter is

wheres the numerical value of the blocking volume fraction when the thermodynamic limitNgoes to infinity.Atφ=hyshould intersect for differentNcurves with a common valuehf(0),as shown in Fig.6,where the curves of different system sizes collapse to a common scalar curve.hydenotes the fraction of order parameter identified by the DL model in the predicted dataset,givenNandφ.WhenNtends to infinity,hywill represent the order parameter of the system located in different volume fractions, which is sufficient to represent the variation of this one system: at small volume fractions,the particles are free to move without overlap and do not consume any energy,when the system is in a fluid state.At higher volume fractions,the particles are forced to squeeze together and overlap with each other to form a force network across the whole system.At this point, the system is able to resist compression or shear, has a non-zero bulk elastic modulus and shear modulus, behaves as a solid, and the system undergoes a jamming transition.

Fig.6.Finite-scale scaling analysis of the order parameter of systems of different sizes.The system size ranged from N=128 to N=1024,and the curves for the different systems collapsed to a common scaling curve.

We are able to directly derive new order parameters that quantify the features of two-dimensional non-crystals from the thermal maps generated by the Grad-CAM model.The model generates descriptions of these features based on only amorphous particle configurations, not relying on environmental descriptions or a set of reference structures.This illustrates that our deep learning model is an effective tool for identifying structural features of complex amorphous systems.

4.Conclusion

In this work, we demonstrated that the interpretability deep learning model we constructed enables classifying amorphous configurations while identifying structural features in amorphous materials.We simulated amorphous systems with different particle numbers according to molecular dynamics,and achieved accurate classification of 2D amorphous configurations with DL models, achieving good results on different amorphous systems with an accuracy of 92.75%.The DL model was visualized by the class activation of the configuration data by the Grad-CAM method,highlighting the important structures of the liquid and amorphous solid configurations.Further,we extract from the heat map and derive an order parameter that provides a quantifiable explanation for the amorphous structure feature identification results.The order parameter can represent the process of liquid to amorphous solid structure in the system, and the change law meets the finite scale effect.

In theory,our DL model can be applied to other complex amorphous material classification, and only by using enough data to train the network, the resulting model can accurately distinguish between different categories of data, which will make part of the work of physical research simple and fast.Our model generates amorphous, feature descriptions based only on 2D amorphous particle configurations,which provides important tools for the study of amorphous structure features,demonstrating that deep learning algorithms can effectively identify structures in complex systems.

From the present results, it is not theoretically possible to accurately describe the amorphous structural features, so we hope to continuously improve the model structure.In the next step,we will consider optimizing the deep learning model combined with the physics theory,which can have a theoretical basis when explaining the non-crystal structures.At the same time,we can extract the local particle structure information of the amorphous material,and quantify and predict it combined with the physics, so as to make the deep learning analysis of the amorphous material structure more effective.

Acknowledgements

Project supported by National Natural Science Foundation of China(Grant No.11702289),the Key Core Technology and Generic Technology Research and Development Project of Shanxi Province,China(Grant No.2020XXX013),and the National Key Research and Development Project of China.