Multi-band analysis on physical properties of superconducting FeSe films

Jian-Tao Che(车剑韬) and Chen-Xiao Ye(叶晨骁)

1Department of Mathematics and Physics,North China Electric Power University,Beijing 102206,China

2School of Nuclear Science and Engineering,North China Electric Power University,Beijing 102206,China

Keywords: Ginzburg–Landau theory,two-band s-wave superconductivity,FeSe film

1.Introduction

The discovery of iron-based materials with high superconducting transition temperatures has triggered great interest for both fundamental research and practical applications in this field.[1]Among these superconductors, the FeSe system has the simple crystal structure, clean superconducting phase, and low toxicity, thus making it an appealing candidate for studying the superconducting properties of iron-based compounds.[2]Although the superconducting transition temperature for bulk FeSe is relatively low(Tc～8 K),[2,3]it can be significantly enhanced by applying high pressure,[4–6]intercalating alkali metal atoms like potassium[7–15]or most amazingly, by growing FeSe thin films on SrTiO3substrates with reported values ofTcup to 100 K.[16–18]Several approaches to the deposition of FeSe films such as pulsed laser deposition and molecular beam epitaxy techniques have been reported so far.[19–21]The FeSe layers consist of square lattices of Fe atoms with tetrahedrally coordinated covalent bonds to the Se anions, and the lattice constant perpendicular to the layered plane is about 0.55 nm.[22]This textured structure is suitable for research of low-dimensional electronic transport on substrates.For instance,Farraret al.have observed signatures of the Berezinskii–Kosterlitz–Thouless transition for FeSe thin films and reported that a highly two-dimensional pairing channel dominates the superconductivity in this system.[23]

Recent studies on the electronic band structures have suggested that strong electron correlation plays a crucial role in understanding the physical properties of the FeSe compound.Based on dynamical mean field calculations,the existence of a lower Hubbard band is demonstrated for the electronic structure and this correlated electron system exhibits the non-Fermi liquid behavior due to the formation of local moments over an extended temperature range.[24]With soft-x-ray and hardx-ray photoemission spectroscopy, the detection of the Fe 3d band narrowing and the energy shift of the band toward the Fermi level also indicate the importance of the electron correlation effect in FeSe.[25]Later,Jianget al.pointed out that the Fe–Fe interatomic Coulomb repulsion actually offers a natural explanation for the emergent nematic order, the absence of magnetism,and at a more fundamental level,the unusually large band renormalization in the FeSe system.[26]Based on the extended Hubbard model,it has also been argued that the interatomic Coulomb interactions favor s-wave pairing[27]and will play an important role in stabilizing the s-wave pairing symmetry in Fe-based superconductors.[28]

To date, there have been several investigations on the pairing symmetry of the superconducting FeSe film.The experimental data of superfluid density for an ultrathin FeSe system can be fitted down to 10 K using the standard Bardeen–Cooper–Schrieffer (BCS) theory, which gives a gap of 10.1 meV at zero temperature and shows the nodeless structure in the excitation spectrum.[29]However, the unusual upturn of the superfluid density around 5 K may also point to the presence of a second (small) gap in this system.Meanwhile, the measurements from the scanning tunneling microscopy have reported the gap structure with double peaks at 2.3 meV and 1.5 meV for the superconducting state of the FeSe compound.[30]Moreover, the anisotropy of the upper critical fields decreases with the decreasing temperature and reveals a pseudoisotropic behavior in this process, which is also indicative of the multi-band character for this material.[31]The strong temperature dependence of Hall sensitivity for the FeSe film shows the similar effect.[32]Thus, there is still no general consensus on the form of superconducting order parameter in the FeSe film to date, and further explorations to elucidate this issue are necessary.

The main purpose of this paper is to investigate the electromagnetic properties of the FeSe film using the two-band Ginzburg–Landau (GL) theory.We derive the two-band GL equations for the two-gap superconducting film,and then compute the temperature dependence of upper critical field in arbitrary direction and critical supercurrent density through this system.It is found that the normalized upper critical fieldHc2(T)/Hc2(0) is independent of the film thickness and all the results are in good agreement with the experimental data.These thus suggest that the FeSe film system is a two-gap swave superconductor.As a byproduct, our calculations also show that the ratio of the effective masses between these two bands is about 6.2.

The rest of this article is organized as follows.In Section 2, we introduce the two-band GL theory and apply this formalism to the quasi-two-dimensional superconductor.In Section 3, we compute the temperature and angular dependence of upper critical fields in the FeSe film.In Section 4,we calculate the temperature dependence of critical supercurrent density through the film.Finally, we conclude this article in Section 5.

2.The two-band Ginzburg–Landau theory

The GL free energy functional of two-gap superconductor with a small thicknessdalong thez(orc)direction can be written as[33–40]

with

wherefγis the free energy density for bandγ(γ= 1,2),f12is the interaction free energy density between these two bands,Δγis the superconducting order parameter,mγrepresents the effective mass for bandγ, andε12is the Josephson coupling constant.The coefficientαγis a function of temperature, whileβγis independent of temperature.If the interband interaction is neglected, the GL functional can be reduced to two independent single-band problems with corresponding critical temperaturesTc1andTc2,respectively.Thus,the coefficientαγcan be approximately expressed asαγ(T)=αγ0tγ(T)=αγ0(1-T/Tcγ),withαγ0being the proportionality constant.[41]H=∇×Arepresents the magnetic field andAis the vector potential.

Actually the GL functional for the two-gap superconductor can be derived from the two-band BCS model,and the microscopic forms of all the parameters in the GL theory have been obtained in Ref.[35].Without loss of generality, we can assume thatTc1corresponds to the band with the larger gap.With ln(Tc1/T)≈t1(T),we can expand the microscopic forms ofα1andα2as linear functions oft1(T),and obtain the useful relationα10/α20=Tc1/Tc2.Since two gaps at low temperature appear at 2.3 and 1.5 meV, respectively,[30]we can roughly approximateTc1/Tc2to 2.3/1.5≈1.5 from the BCS theory.Meanwhile,from the microscopic two-band BCS theory we can also obtainβ1=β2≡β.[35]We notice that the GL free energy in Eqs.(1)–(3)is invariant under the scaling transformation:ε12→ε12/lwithlbeing the scaling factor.Thus for simplicity,we can setm2=mewithmethe electron mass.

For a smooth nonmagnetic insulator-superconductor or vacuum-superconductor interface, we assume that there is no current flowing through the boundary and the Neumann boundary condition can be applied on the macroscopic scale.Thus,the boundary conditions on both surfaces of the thin film are given byIt is easy to see that if we approximate the order parameterΔγto a constant along thez-axis,the Neumann boundary condition will be automatically satisfied.

3.The upper critical field

Now let us solve the problem of the nucleation of superconductivity in the presence of magnetic fieldH.Without losing any generalization, we assumeH=(Hsinθ,0,Hcosθ),whereθis the directional angle of the field from thez-axis.Then the vector potential can be chosen asA=(0,Hxcosθ-Hzsinθ,0).Noting thatAis only related toxandz, we can write the solution in the form ofΔγ(x,y,z)=ργ(x,z)eikyy.Plugging this form into Eqs.(2) and (3), and neglecting the quartic terms in the free energy densities, we can rewritefγandf12as

Meanwhile, the requirement of the Neumann boundary conditions demands that in the lowest order the wavefunctionργwill have nozdependence,i.e.,ργ(x,z)=ργ(x).With this approximation, we then perform the integration onzin Eq.(1)and obtain the total free energy as follows:

Here we define

By minimizing the free energy withργin Eq.(6),the linearized two-band GL equations in the thin film can be written as

Obviously, the inclusion of the factorx0only shifts the location of the minimum of the effective potential, so it will be neglected hereafter.

In the absence of the magnetic field and close to the critical temperature,ργcan be treated as constant, then Eqs.(8)and(9)are simplified to

From Eq.(10),we can obtain=α1(Tc)α2(Tc),which will be used to determineε12in our calculations.

Now we try to work out the upper critical field of the FeSe film under the applied magnetic field.In the case ofε12=0,we can obtain the solution to Eqs.(8)and(9)immediately by noting that,for each band,it is the Schr¨odinger equation for a particle bound in a harmonic oscillator potential.The resulting eigenvalues areEγ,n=(n+1/2)¯hωγ+σγwithnbeing a nonnegative integer,and the ground wavefunctions corresponding to these two bands take the form of (ν0/π)1/4e-ν0x2/2, withν0=2πH/Φ0and the magnetic flux quantumΦ0=π¯hc/e.

Ifε12/=0, Eqs.(8)and(9)describe a system of the two coupled oscillators.To obtain the minimum eigenvalue of the coupled oscillators,we follow a variational approach.We propose the solution in the form ofργ=aγ(ν0/π)1/4e-ν0x2/2,whereaγis constant.Thus forn=0,Eqs.(8)and(9)can be transformed to

Then the upper critical fieldHc2can be obtained from Eq.(11)as

atH=Hc2.

Whenθ=0°,from Eq.(12)we can obtain the exact expression of the upper critical field parallel to thez-direction as

Forθ=90°,we can obtain the upper critical field perpendicular to thez-direction as

Here= ¯h2/m2α20and the effective mass anisotropyηm=m1/m2.

Fig.1.The temperature dependence of normalized upper critical field parallel to the c-axis for the FeSe film thickness d =14 nm, 24 nm,58 nm,and 100 nm.The experimental data are taken from Ref.[23].

Fig.2.Temperature dependence of normalized upper critical field perpendicular to the c-axis for the FeSe film.The experimental data of the FeSe films with the thickness d=14 nm,24 nm,58 nm and 100 nm are taken from Ref.[23].

We can easily obtain from Eqs.(13) and (14) that the normalized upper critical fieldsHc2(T)/Hc2(0) are independent of the film thicknessd, and can be explicitly calculated with two scale-invariant parametersηmandηt=Tc1/Tc.We chooseηm=6.2 andηt=0.93 to fti the experimental data of theFeSe flims.FromFig.1,we can seethatthe data points ofarealmost linearin the wholetemperature range belowTcand our calculations are consistent with the experimental measurements.Due to the simple relation betweenandin Eq.(14), our theoretical results ofshow the parabolic behavior and also well fit the experimental data with various film thicknesses in Fig.2.

Furthermore,we can also perform the numerical computations on the angular dependence of the upper critical field according to Eq.(12).By taking one more parameterξ0=0.36 μm, we plot our results atT=2 K for the 14 nm-thick FeSe film in Fig.3.From Fig.3, we can see that the upper critical fieldHc2increases monotonously with the angleθand our numerical calculations are consistent with the experimental data.

Fig.3.Angular dependence of upper critical field at T =2 K for the FeSe film.The experimental data of FeSe with the thickness d=14 nm are taken from Ref.[23].

Fig.4.The anisotropy parameter of the upper critical fields as a function of temperature for the FeSe film.The experimental data of the 520 nmthick FeSe film with length 750 μm and width 150 μm are taken from Ref.[31].

In this stage, we can also define an anisotropy parameter for the upper critical fieldsand plot it as a function of temperature in Fig.4.From Fig.4, we can see thatγHdecreases with the decreasing temperature and our calculations are in accordance with the experimental data.Since temperature-independent behavior ofγHis expected for single-band superconductors,this temperature dependence is a manifestation of multi-band superconductivity.[42]All of our theoretical results thus strongly suggest the two-gap s-wave superconductivity in this material.

It is worth noting that from the fitting of our numerical data the band with the larger gap corresponds to the larger effective mass, and the ratio of effective masses between these two bands equals 6.2, which is consistent with the effective mass anisotropyηm=5.7 from the measurement of the angleresolved photoemission spectroscopy.[43,44]

4.The in-plane critical supercurrent

We can easily rewrite the GL free energy Eq.(1)with the form ofΔγfollowing the standard procedure[45]

Then,for the fixedvswe can minimize Eq.(15)with|Δγ|and find the optimum value of|Δγ|satisfying

whereDγ(T)=-αγ.We can solve Eqs.(16)and(17)to the cubic order of|Δγ|and obtain

Similar to the single-band case,[45]we thus calculate the uniform supercurrent density from the two-band GL theory as

With Eq.(19),we can apply the conditionfind the maximumj(T),which is exactly the uniform critical supercurrent densityjc(T).It is easy to see from Eq.(19)that the ratio of critical supercurrent densityjc(T)/jc(0) is independent ofβ,and we plot our results in Fig.5.From Fig.5,we can see that our numerical calculations can fit the experimental measurements in a wide temperature range,and especially the positive curvature behavior nearTc,which generally indicates the multi-band character of the corresponding systems.

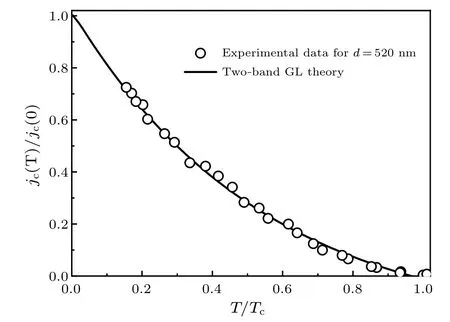
Fig.5.Temperature dependence of critical supercurrent density for the FeSe film.The experimental data of the 520 nm-thick FeSe film with length 750 μm and width 150 μm are taken from Ref.[46].

5.Conclusion

In summary, based on the two-band GL theory we have investigated the temperature and angular dependence of the upper critical field in the FeSe thin film.It is found that the normalized upper critical field as a function of temperature is independent of the film thickness and our results are consistent with the experimental data.Furthermore, we also calculate the critical supercurrent density through the FeSe system which is also in accordance with the experimental measurements.Combining all of these facts,our theoretical work thus strongly suggests that the FeSe film is a two-gap s-wave superconductor.In addition,our mean-field analyses also show that the band with the larger gap corresponds to the one with the larger effective mass,and the ratio of the effective masses between these two bands is about 6.2.We hope that our theoretical results will inspire further research on better understanding the pairing symmetry and superconducting properties in ironbased materials.

Acknowledgment

It is a great pleasure to thank Professor H.Huang for patient guidance and helpful discussion.