Hole density dependent magnetic structure and anisotropy in Fe-pnictide superconductor

Yuan-Fang Yue(岳远放), Zhong-Bing Huang(黄忠兵), Huan Li(黎欢),Xing Ming(明星), and Xiao-Jun Zheng(郑晓军),‡

1College of Science,Guilin University of Technology,Guilin 541004,China

2Key Laboratory of Low-dimensional Structural Physics and Application,Education Department of Guangxi Zhuang Autonomous Region,Guilin 541004,China

3Faculty of Physics,Hubei University,Wuhan 430062,China

Keywords: iron-pnictide superconductors,magnetic structure,resistivity anisotropy

1.Introduction

The phase diagram of Fe-pnictides is very similar to the one in copper oxides, in the sense that the high temperature superconductivity emerges in both materials when an antiferromagnetic(AFM)state is suppressed by carrier doping.For this reason,understanding the nature of the magnetism and its doping dependence in these materials is believed to be key in explaining their high-Tcsuperconductivity.[1–6]

The nature of the magnetism in Fe-pnictides is, however, quite different from the one in cuprates.Firstly, unlike the (π,π) ordered antiferromagnets in the undoped cuprates,the parent phase in Fe-pnicitides is a stripe-like antiferromagnetic (str-AFM) state with a wave-vectorQ1=(π,0) orQ2=(0,π).[7,8]This str-AFM state breaks the tetragonalC4point-group symmetry of the system down to the orthorhombicC2symmetry, and it is accompanied by a tetragonal-toorthorhombic structural distortion and in-plane anisotropies in several observables, such as an orbital ordered polarization of dxzand dyzof Fe,[9,10]anisotropies in the optical spectrum,[11,12]as well as anisotropic dc conductivities.[13]Secondly,unlike the strong correlated antiferromagnetic Mott insulator phase with an electron occupationn=1(half-filling)in the parent cuprates, the parent antiferromagnetic phase of Fe-pnicitdes is a weak/moderate correlated bad metal with an electron fillingn=6 per Fe(with an average orbital occupationnobt=n/5=1.2).[7,8]

Various techniques demonstrate that in hole doped Fepnictide,the effective mass of carriers is enhanced as the filling is reduced,namely,electronic correlations increase monotonically with hole doping.[14–29]This behavior is understandable asnobtapproaches half filling by hole doping.However,contrary to the significant enhancement of the correlations,it is intriguing to note that the magnetism is rapidly suppressed as the hole-carriers are doped into the system.Moreover, Muon spin rotation and infrared spectroscopy study showed that the Fe magnetic moment is only moderately suppressed in most of the underdoped region where it decreases more slowly than the Neel temperatureTN.[30]This result indicates the complexity of the magnetism in the hole-doped Fe-pnicitdes,and a further investigation is needed to reveal why the electronic correlation and magnetism behave in the opposite way.

Besides the magnetism, the evolution of the in-plane resistivity anisotropy with hole doping is also intriguing and unusual.Recently, it was observed that the anisotropy resistivity changes sign fromρb-ρa ＞0 toρb-ρa ＜0 across the doping phase diagram of Fe-pnictides.[31,32]This behavior has been widely discussed while the mechanism behind it is still controversial.[33–36]More intriguingly, a temperature-dependent sign reversal was observed in holedoped Ca1-xNaxFe2As2.[32]That is, the anisotropic transport evolves fromρb-ρa ＞0 at high temperature, but still underTN, toρb-ρa ＜0 at low temperature.This behavior can not be explained by the spin fluctuation[33–35]and the ellipticity of the FSs[31,36]since under the magnetically ordered state the FSs are strongly renormalized.Instead, it indicates that there may be a competition between different orders at this level of hole doping, and it is likely that their contributions to the resistivity anisotropy are diverse and temperature dependent.[32]

In this study, we perform a comprehensive investigation on the hole-doping dependent magnetism of Fe-pnictides based on a five-orbital extended Hubbard model.[37–39]The primary result of our study is that the magnetic structures of Fe-pnictides evolve with hole doping.The stabilities of the magnetic structures are demonstrated to be very sensitive to the hole-doping levels, as a result, fierce magnetic competition/frustration emerges at certain hole concentrations.Namely, when the str-AFM structure is dominant in the parent phase, magnetic structures with an increasing number of nearest-neighbors antiferromagnetic links, such as the staggered tetramer antiferromagnetic(tet-AFM)state withQtet=(π,π/4), staggered trimer antiferromagnetic (tri-AFM) state withQtri=(π,π/3) and staggered dimer antiferromagnetic(dim-AFM)state withQdim=(π,π/2),become energetically more favorable as hole doping increases.

We argue that this hole-doping induced magnetic competition and magnetic frustration may contribute to the suppression of long-range magnetic ordering, which has been discussed in the case of FeSe,[40]and it may explain the fast decrease of the Neel temperatureTNand the moderately suppressed magnetic moment in the hole-doped Fe-pnicitide.What’s more, we find that the signs of the kinetic energy anisotropies are different for different magnetic structures, as a result, the kinetic energy anisotropy of the system changes sign as the magnetic structures evolve with doping,which we believe is responsible for the sign reversal of the resistivity anisotropy that observed experimentally.

Our paper is organized as follows: In Section 2, we define the Hamiltonian and describe the calculation methods.In Section 3, we present our numerical results and discuss their relation to the experimental measurements.Finally,we make some concluding remarks in Section 4.

2.Model

The tight-binding model we use is the one derived by Kurokiet al.[41]As one of the most intensively studied models for Fe-pnictides, it has explained or well reproduced a variety of experimental phenomena, not only for LaFeAsO but also for other classes of Fe-pnictides.Therefore, in this paper we focus on this tight-binding model, irrespective of other Fe-pnictides models which may have some difference in the electronic structures but do not affect the basic physical properties.[42]The electronic correlations we consider here include the intraorbital and interorbital Coulomb interactionsU1andU2,the Hund’s couplingJ,and the off-site Coulomb interactionVbetween nearest-neighbor(NN)sites:

The reason we includeVinto the Hamiltonian is thatVhas been proved to have an important effect on the properties of iron-based superconductors, especially on the nematicity and magnetism.In the following we show that the introduction ofVimproves the magnetism’s sensitivity to hole doping.For simplicity,in our calculations we propose thatVis orbital independent, and its value is set to be 0.5–0.75 eV according to theab initiocalculation.[43]What’s more, to eliminate the double counting ofV,we subtract the purely electrostatic term,which corresponds to the first term of the following expression:

One can see that the first term in Eq.(2) depends on the average density on the sites, thus it is reasonable to assume that this term is already captured by the DFT.[44]Thus,in our following calculations we subtract it to eliminate the double counting.The second term is the exchange term which modifies the hopping amplitudes and leads to the renormalization of the band structure.[39,45]

In our calculations, the expectation value of the interaction Hamiltonian is evaluated by Wick’s theorem,and the twooperator contractions of the form〈φ1φ2〉(whereφrefers tociorwill only be considered when they keep the symmetries of the original Hamiltonian.

The mean-field wave functions|ψMF〉 for the magnetic phase are the ground states of the following mean field Hamiltonian:

HereΔMdenotes the magnetic ordering parameters.The magnetic wave vectors are set to beQstr=(π,0),Qtet=(π,π/4),Qtri=(π,π/3), andQdim=(π,π/2), corresponding to str-AFM structure,tet-AFM structure,tri-AFM structure and dim-AFM structure, respectively.All these four magnetic structures are illustrated in Fig.1.

Fig.1.Pattern definitions for the magnetic structures: (a)str-AFM,(b)tet-AFM,(c)tri-AFM,(d)dim-AFM.

3.Results and discussion

Considering that the interaction strength in Fe-pnictides is moderate and material dependent,in our calculation we setU1=2.0–3.0 eV, andJ/U1=0.15, 0.20, 0.25, with a wellknown relationU2=U1-2J.The magnitude ofVis set toV/U1=0.25, which is reasonable according to theab initiocalculations.In Fig.2 we present the magnetic phase diagram as a function of dopant concentrations and interaction strengths.We can see that the magnetic structure of the system evolves from str-AFM to dim-AFM as occupation number changes fromn=6.1 ton=5.5.Aroundn=6.0,the str-AFM state dominates, which is in agreement with experiments for underdoped Fe-pnicitdes.Asndecreases,the str-AFM is substituted by a tet-AFM state or a tri-AFM state.ForJ=0.15U1[Fig.3(a)], the str-AFM to tri-AFM phase transition emerges already aroundn=6.0 forU1≤2.2.ForU1≥2.2,a str-AFM to tet-AFM transition emerges asndecreases to 5.8,followed by a tet-AFM to tri-AFM transition aroundn=5.71 and a tri-AFM to dim-AFM transition aroundn=5.61.WhenJ/U1increases to 2.0[Fig.3(b)]or 2.5[Fig.3(c)],the region of str-AFM dominants expands,and the critical occupation number,ncrt, around which the phase transitions emerge slightly decreases.From Figs.2(a)–2(c)we can see that the stabilities of the magnetic states are sensitively dependent on the occupation number.As the hole doping increases,the magnetic state with an increasing number of nearest-neighbors antiferromagnetic links, such as tet-AFM,tri-AFM and dim-AFM phases,becomes successively the energetically favorable state.Details may depend on the variations of the correlation strength, but the general trends are robust.

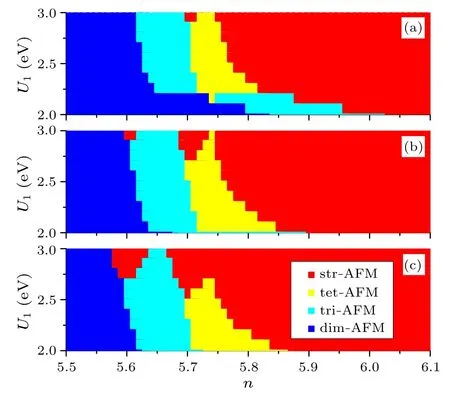
Fig.2.Mean-field magnetic phase diagram as a function of U1 and n.The relation U2=U1-2J is kept,J/U1=0.15,0.20,and 0.25 for(a),(b),and(c).

Fig.3.Energies of the magnetic states refer to the energy of the str-AFM state as a function of n for(a)R=0.0,(b)R=1.0,(c)R=2.0,(d)R=3.0.

As mentioned above,the electron correlation strength increases with hole doping.With this in mind,we perform calculations in which the correlation strength increases linearly as hole doping increases.Specifically,we set

HereRis the scaling factor which determines the increasing rate of the correlation strength as hole doping increases.For example,by choosingR=1.5,we haveU1increasing from 2.2 eV to 3.4 eV asndecreases from 6.1 to 5.5.Jincreases from 0.33 eV to 0.51 eV,U2increases from 1.54 eV to 2.38 eV,Vincreases from 0.55 eV to 0.85 eV, by settingJ=0.15U1,U2=U1-2J,andV/U1=0.25.

In Fig.3, we present the energy differences between the str-AFM state and the other magnetic states as a function ofnforR=0, 1.0, 1.5, and 2.0.We can see that when the energy differences increase withR, the general trend is robust.Namely,asndecreases,the tet-AFM,tri-AFM and dim-AFM states become more energetic favorable successively.The first energy degeneration emerges at around 5.75≤n ≤5.80, depending on the value ofR.These results indicate a hole-doping introduced magnetic frustration, and we suggest that it may contribute to the experimentally observed dropping ofTN.

Fig.4.(a)Orbital occupation number nα and(b)orbital magnetic moment mα in the str-AFM state as a function of the site occupation number n.

In Fig.4, we present the orbital occupation numbernαand orbital magnetic momentmαin the str-AFM state as a function of the site occupation numbern.One can see that whennxzdecrease sharply with decreasingncompared to other orbital occupation numbers,mxzincreases fast with decreasingn.We note thattxz,xz[0,ay] is much larger thantxz,xz[ax,0] in our model, namely, the NN exchange coupling between the spins on thexzorbitals is anisotropic with they-direction dominant thex-direction.Thus,as the orbital momentnxzincreases with hold doping as shown in Fig.4(b),the total NN exchange coupling along they-direction will enhance.As a result,the magnetic structures with an increasing number of NN antiferromagnetic links along they-direction become energetically more favorable as hole doping increases.Our results demonstrate that orbital differentiation is crucial to address the magnetic softness and doping properties of Fepnictides.

Fig.5.(a) Energies of the magnetic states refer to the energy of the str-AFM state as a function of n.(b)Anisotropy of the kinetic energies obtained in the magnetic states as a function of n.The vertical dashed lines indicate the doping point at which the str-AFM state and tet-AFM state are degenerate.

4.Conclusions

In summary, we have carried out a comprehensive investigation based on a realistic extended five-orbital model.Our results demonstrate that the stability of magnetic structure is very sensitive to the hole-doping levels and magnetic frustrations arise due to the fierce competition between magnetic structures at certain levels of hole doping.We consider that these frustrations contribute to the experimentally observed dropping ofTNwith hole doping, explaining the intriguing magnetic behavior which is contrary to the electronic correlation.What’s more,our results show that the kinetic energy anisotropies change sign as the stabilized magnetic states change with doping, which may be responsible for the puzzling sign reversal of the resistivity anisotropy found in holedoped Ca1-xKxFe2As2.

Acknowledgments

Project supported by the Guangxi Natural Science Foundation, China (Grant Nos.2022GXNSFAA035560 and GuikeAD20159009) and the Scientific Research Foundation of Guilin University of Technology (Grant No.GLUTQD2017009).