Infrared optical absorption of Fr¨ohlich polarons in metal halide perovskites

Yu Cui(崔钰), Xiao-Yi Liu(刘晓逸), Xu-Fei Ma(马旭菲),Jia-Pei Deng(邓加培), Yi-Yan Liu(刘怡言), and Zi-Wu Wang(王子武)

Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparing Technology,Department of Physics,School of Science,Tianjin University,Tianjin 300354,China

Keywords: metal halide perovskites,polaron,Huang–Rhys factor

1.Introduction

The formation of Fr¨ohlich polarons (or large polarons)originates from the coupling between a macroscopic electronic field induced by the polar optical phonon modes in a solid and a charge carrier.Such polarons are also called special carriers dressed by the ‘phonon cloud’ (the induced nuclear polarization),reflected by the average phonon number.[1–3]This type of polaron has aroused much interest in relation to metal halide perovskites(MHPs)because it has been used to unlock key puzzles regarding their exceptional properties,[4–7]such as their moderate carrier mobility, large carrier diffusion length,long carrier lifetime and high defect tolerance.Therefore,the identification of this type of polaron in MHPs has become a crucial problem in both experimental and theoretical studies.

In the past few years,the formation of Fr¨ohlich polarons in perovskite materials has been probed in spectral measurements: following the polaron formation dynamics in timeresolved optical Kerr effect spectroscopy,[8]ultrafast terahertz(THz) spectroscopy[9]as well as time-resolved two-photon photoemission and transient reflectance spectroscopies;[10]examining Pb–I structural dynamics in time-domain Raman spectroscopy;[11]and studying the electronic structure in angle-resolved photoelectron spectroscopy.[12]On the other hand, large polarons can be also investigated by other measurements such as the mobility of charge carrier scaling with temperature in transport[13]and Hall effect measurements.[14]From a theoretical perspective, large polarons forming predominantly from the distortion or deformation of the crystal structure with first-principles calculations have also been widely studied.[15–17]Despite the experimental and theoretical evidence confirming the formation of large polarons in perovskite materials,detailed knowledge and direct distinction of the‘phonon cloud’of a polaron,which is the crucial ingredient determining the nature of the polaron,are not well understood to date.

In this paper, we theoretically study the infrared optical absorption of Fr¨ohlich polarons in three-dimensional(3D)and two-dimensional(2D)MHP materials stemming from the strong electron–longitudinal optical (LO) phonon mode coupling.We find that the ‘phonon cloud’ of a polaron can be directly reflected by the multiple LO phonon structure of the optical absorption spectra,in which the average phonon numbers described very well by the dimensionless Huang–Rhys(HR)factor are directly linked to the order of the strongest absorption peak.Moreover,the strongest absorption peak shifts to the higher order with decreasing electronic distribution radius in the ground state, indicating that the range of the electronic distribution plays an important role in determining the electron–LO phonon coupling.Meanwhile, the temperature dependence of the polaron absorption processes is also discussed.

2.Theoretical method

As depicted in Fig.1,the absorption of light by polarons can be described as follows: when the incident photon energy¯hωmatches the energy of the multiple LO phononsp¯hωLO,the polaron system will undergo transitions from the ground state|Ψi〉=|ψ1s〉|χin′q〉with energyEitowards a series of excited states|Ψf〉=|ψ1s〉|χfnq〉with energyEf=Ei+p¯hωLO.|ψ1s〉is the ground state of the polaron and|χin′q〉(|χfnq〉)is the initial (final) lattice wave function, wheren′q(nq) is the occupation number for phonons with the wave vectorq.Note that the optical absorption discussed here is one-polaron behavior rather than that of a many-polaron gas.As is typical of multiphonon transition process, it is excellently described by the HR model.[18–21]By means of this well-known model,the probability of optical absorption for light with frequencyωcan be expressed as[22–24]

whereeis the charge carrier, ¯hωis the photon energy,mis the effective mass of the polaron,εis the permittivity,cis the velocity of light andrrepresents the position variables for polaron.Here the spatial average〈|ri f·E0|2〉=|ri f|2|E0|2/3 and the relation ¯hω=εc|E0|2/(8π)for the electronic dipole approximation have been used.[25]

Fig.1.Schematic diagram of optical absorption of the polaron, where¯hω is the incident photon energy and ¯hωLO is the longitudinal optical(LO)phonon energy.

For the ground state of polaron,a Gaussian wave function is considered:[26]

LO phonons are mainly taken into account because they couple with the charge carriers in the Fr¨ohlich mechanism as the main source of lattice distortion for MHP materials not only in theory but also in experiments.is the phonon number occupation function wherekBand¯hωLOare the Boltzmann constant and LO phonon energy, respectively,andIpis thepth-order imaginary argument Bessel function with the phonon numberp.σrepresents the line-width of the phonon overtone.The strength of electron–phonon coupling has been characterized using the HR factorSλ, which plays a nontrivial role in determining multiphonon processes.In the Fr¨ohlich mechanism,[26,31,32]the HR factor can be calculated by

whereℓ3D(q) = 4πα/(Vq2) andℓ2D(q) = 2πα/(Aq).The detailed derivations for the HR factor, charge carrier–LO phonon coupling, the corresponding definition and expression of parameters are shown in the supplemental materials.In the numerical calculation processes,we choose typical MHPs CH3NH3PbI3(MAPbI3), CH3NH3PbBr3(MAPbBr3)and CH3NH3PbCl3(MAPbCl3) as examples to discuss the optical absorption processes of the polaron.The line-width of the phonon overtone is usually around a few meV,[2]and throughout this paper the line-widthσ= 3 meV is assumed.The adopted values of other parameters for the three types of materials are shown in Table 1, and are measured by temperature-dependent photoluminescence and far-infrared spectroscopy.[33,34]

Table 1.The adopted parameters for the theoretical calculations(m0=9.1×10-31 kg is the free electron mass).

3.Results and discussion

The HR factor was originally proposed by Huang and Rhys for F-centers in ionic crystals in 1950;[18]it denotes the average phonon numbers around F-centers,reflecting the magnitude of lattice distortion arising from the strong coupling between electronic states and lattice vibrations (phonons).Herein, the HR factor is invoked to describe the ‘phonon cloud’ of the polaron with relaxation energySλ¯hωLO.The dependence of the HR factor on the electronic distribution radius in the ground state in different dimensionalities is shown in Figs.2(a) and 2(b) for MAPbI3and MAPbBr3, respectively.One can see that the HR factor increases from 3D to 2D, stemming from that both the reduced dielectric screening and increased degree of quantum confinement are held responsible for the enhancement of electron–phonon coupling.On the other hand, the HR factor exhibits a negative correlation witha0.But the HR factor varies smoothly asa0exceeds 0.6R0(R0being the polaron radius).This indicates that outside this region the localization feature of electrons has little effect on electron–phonon coupling.Numerous researchers have calculated the formation energy of large polarons.The obtained values range are 12 meV for 3D MAPbI3and 16±2 meV for 3D MAPbBr3in a tight-binding model fitted from the first-principles calculation and temperaturedependent absorption spectroscopy,[35,36]respectively.These numerical values are in good agreement with the relaxation energyS3D¯hωLO≈13.8 meV for 3D MAPbI3andS3D¯hωLO≈18.2 meV for 3D MAPbBr3ata0≥0.6R0, implying that the formation energy can be well described by the relaxation energy.As for 2D perovskite species, although there is little direct information about polarons in the experiments,the discoveries of 2D exciton polarons and self-trapped excitons reveal significant polaronic character.[37–40]The numerical values of HR factors for 2D perovskites in Fig.2 are expected to provide insight for the identification of these quasiparticles.The calculation of relaxation energy can indirectly evaluate the carrier lifetime(carrier lifetime is proportional to the strength of charge carrier–phonon coupling[41]) and thus provide a reference for the selection of more suitable materials for photovoltaic devices.[42]Similar results are also obtained for MAPbCl3in Fig.S2.In addition, it has been shown that the HR factor in MAPbBr3is smallest in these three types of MHP.This is ascribed to the fact that distortion of the Pb–Br bond is more difficult than that of the Pb–I and Pb–Cl bonds determined by the bond length,which is reflected by the coupling parameterαlisted in Table 1.We note that the effective phonon modes and relaxation energy could be obtained from first-principles calculations,[43–45]gaining the more accurate evaluations for the HR factor.Our results will also provide an important theoretical reference for these calculations.

Fig.2.Huang–Rhys(HR)factors in CH3NH3PbI3(a)and CH3NH3PbBr3(b)as a function of the electronic distribution radius in the ground state for different dimensionalities. S2D and S3D represent HR factors in two-and threedimensional perovskite materials,respectively.

On the basis of these theoretical values for the HR factor, the optical absorption spectra of polarons for MAPbI3and MAPbBr3are plotted in Fig.3 for different electronic distribution radii in the ground state, atT=77 K.We first give a detailed discussion of the spectra for MAPbI3.In Fig.3(a), energy resonance absorption will occur when the energy of the incident photon matches that of the multiple LO phonons, showing multiphonon overtones in the infrared(long-wavelength) region of the spectra, where the strongest overtone corresponds to the most probable state of a polaron.The intensities of the overtones follow an asymmetric Gaussian distribution, in agreement with previous experimental measurements.[9,46]Comparison with the HR factors in Fig.2 shows that the order of the strongest overtonepmaxsatisfies the condition ofpmax≈S3D+0.7, such asS3D≈2.42 corresponding topmax=3 ata0=0.4R0, but the condition shifts topmax≈S2D+1 for the 2D perovskites,such asS2D≈3.81 corresponding topmax=5 ata0=0.4R0,which is consistent with our previous results.[47,48]According to our simulation,the curvesS3D+0.7 andS2D+1 are fitted well withpmaxfor 3D and 2D MHPs, as shown in Fig.S7.This means that the average phonon number of polarons can be estimated directly from the absorption spectra.This significant outcome can be used to explain the overtones along with a linear decay from the first to the higher orders in multiphonon Raman scattering and THz time-dominant spectroscopy for CsPbBr3(S3D=0.39).[30]The pronounced redshift behaviors for the position of the spectral weight with the increase in electron localization are shown, specifically manifested in Fig.3(a)as: (1) the number of the observable overtones reduces from seven ata0=0.4R0to five ata0=0.8R0; (2) the most probable state transits from the third order ata0=0.4R0to the second order ata0=0.8R0.These phenomena are direct reflections of the variation in electron–phonon coupling (HR factor) linked to charge carrier localization, showing the polaron to be more stable or more easily taken off the phonon dressing.Similar trends are also obtained for MAPbBr3(in Figs.3(b) and 3(d)) and MAPbCl3(in Fig.S3).Recently,several experiments have proved that large polaron formation drastically suppresses the cooling of hot carriers.[10,49–51]For instance,an envelope of a Cs4PbBr6lattice shell was provided over CsPbBr3nanocrystals.[51]The enhanced strength of the electron–phonon coupling in such shell material facilitates the formation of polarons with a large relaxation energy,and thus depresses the carrier cooling process.It is, therefore, concluded that if more phonon overtones appear in the infrared optical absorption measurements of perovskite materials, the polaron effect will be more pronounced,which could serve as a criterion for judging whether these perovskites materials are suitable for potential applications in photovoltaic(preferring a strong polaron effect)or photoelectronic(demanding fast carrier cooling)devices.

Fig.3.Multiple LO phonon infrared optical absorption spectra in 3D CH3NH3PbI3 (a),3D CH3NH3PbBr3 (b),2D CH3NH3PbI3 (c)and 2D CH3NH3PbBr3 (d)for different electronic distribution radii in the ground state,at T =77 K.

The temperature dependences of optical absorption in 3D MAPbI3, 3D MAPbBr3and 3D MAPbCl3are shown in Figs.4(a),4(b)and S4,respectively.These multiphonon overtones can be divided into two regions: the low-order region including the overtones in the range of 1≤p ≤S3D+2 and the high-order region comprising the rest of the overtones.In the former region,the intensities of overtones decrease monotonically with temperature.On the contrary, the latter region shows the opposite variational trends and even much higher orders of overtones will be thermally activated.This can be explained by more thermally activated LO phonons becoming available with temperature, resulting in (1) the polaron states with more phonons are prone to reach the most probable states and (2) the orders of overtones increase.The blueshift of the most probable states leads to a shift of the whole absorption spectrum towards a higher energy,showing the downward trend of the relative probability in the low-order region and the upward trend for the high-order region, as given in Fig.S5.More importantly, the polaron dressed by more thermally activated LO phonons indicates that the polaron effects are actively strengthened at higher temperature.In perovskite materials,the long carrier diffusion length does not imply a high charge carrier mobility,[8,12,36,52]yet a detailed understanding of its fundamental mechanisms is still outstanding.According to our theoretical study,the polarons become significantly‘heavier’ with temperature because of the blueshift of the spectra mentioned above, which is not beneficial to transport, especially at room temperature.Thus this provides a potential explanation for the moderate carrier mobility in perovskites,which supports the theoretical predictions about LO phonon mode scattering influencing mobility.[34,53]Therefore,it may be more appropriate to elucidate the effective mobility by the polaron model in perovskite materials.[34,36,54–56]In turn,the measurements of the carrier mobility in experiments could also track the path of polarons.[57]It is additionally revealed that the overtones retain a stable outline even at room temperature, implying that polaron states have a very robust lifetime,which will benefit not only experimental observation but also the potential exploitation of polaron properties in perovskite materials.However, there is a prominent distinction for the peaks of overtones with temperature for these three types of material, the details of which are shown in Fig.S6.The variation of the slope indicates that the thermodynamic stability of polarons decreases in the sequence Cl＞Br＞I.As a result, the stability of polarons for MHP materials could suggest application potential in photovoltaics.Finally, we must emphasize that: (1) these perovskite materials undergo two structural phase transitions with temperature,which influence the strength of the electron–phonon coupling and phonon energy;[58–60](2)the rotation of the organic monovalent cation and its coupling with the surrounding inorganic framework affects MHP optoelectronic properties.[61,62]These effects are not taken into account in the present paper.

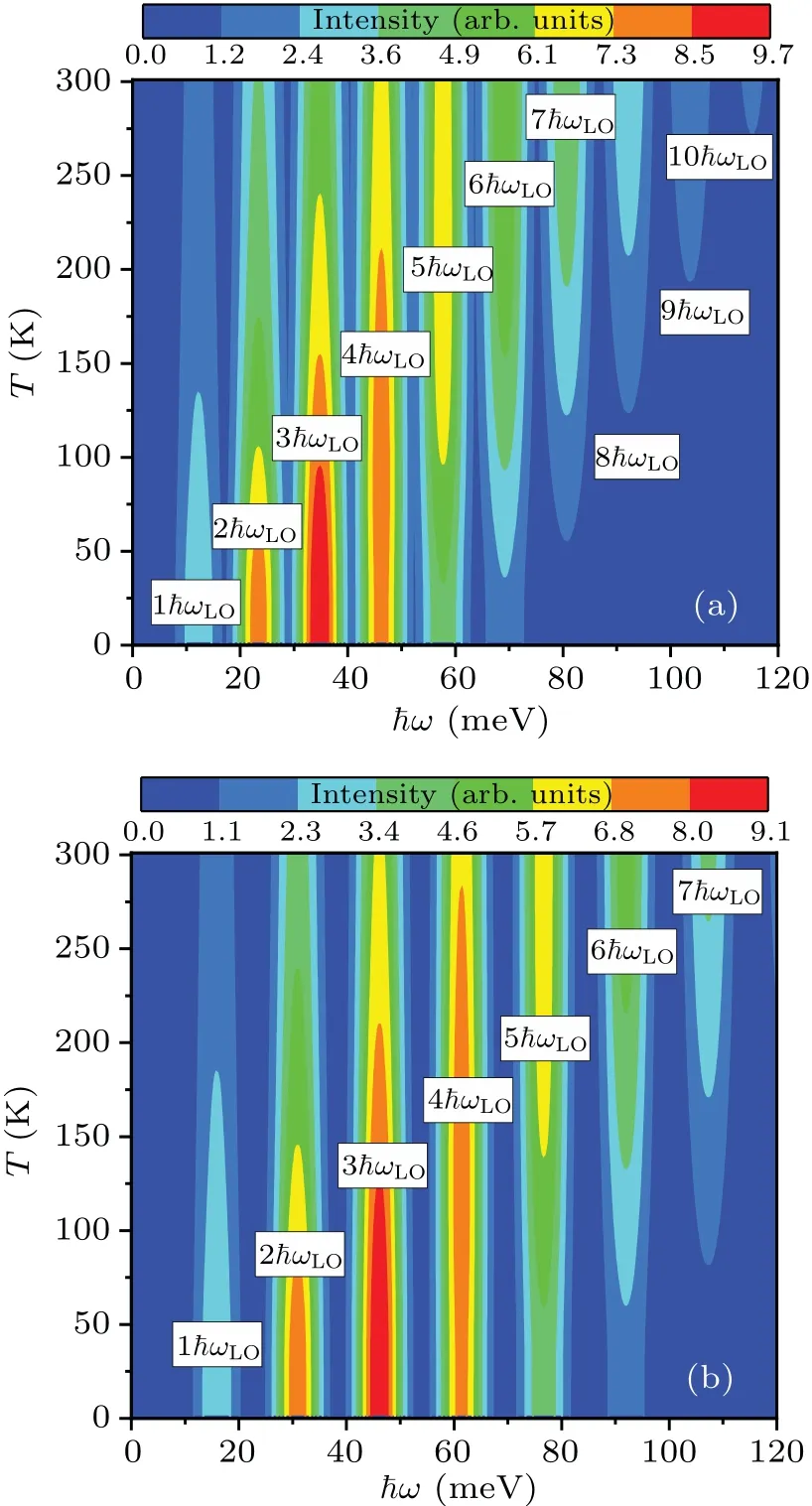
Fig.4.The temperature dependences of multiple LO phonon structures for the optical absorption spectra in 3D MAPbI3 (a)and 3D MAPbBr3(b),respectively,at a0=0.4R0.

4.Conclusion

In summary, we theoretically study the infrared optical absorption spectroscopy of Fr¨ohlich polarons in metal halide perovskites.We find that: (1) the multiphonon structure can be used as the fingerprint of the polaron, where the average phonon number in the ‘phonon cloud’ of the polaron is reflected by the order of the strongest overtone in the absorption spectra; (2) the multiphonon structure sensitively depends on both the dimensionality of the materials and the charge carrier localization, elucidating how competing processes between polaron formation and carrier cooling are controlled,enabling more efficient design of photovoltaic and photoelectronic devices;(3)the‘phonon cloud’around the polaron will become larger as the temperature increases and thus affect the carrier mobility, especially at room temperature, which is consistent with the experimental measurements; (4) infrared optical absorption spectra for MHPs are an easy and effective method,reflecting charge carrier–phonon coupling and ensuring that new materials for energy innovation are designed rationally and appropriately to specific applications.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant Nos.11674241 and 12174283).