SMEFT is falsifiable through multi-Higgs measurements (even in the absence of new light particles)

Raquel Gómez-Ambrosio,Felipe J Llanes-Estrada,Alexandre Salas-Bernárdez,* and Juan J Sanz-Cillero

1 Dipartimento di Fisica,Univ.di Torino,and INFN,Sezione di Torino,Via P.Giuria 1,Torino,10125,Italy

2 Univ.Complutense de Madrid,Dept.Fisica Teorica and IPARCOS,Plaza de las Ciencias 1,Madrid,28040,Spain

Abstract By embedding the Standard Model effective field theory (SMEFT) in the more general Higgs effective field theory (HEFT),we expose correlations among the coefficients of the latter that,if found to be violated in future data,would lead to the experimental falsification of the SMEFT framework.These are derived from the necessary symmetric point of HEFT and analyticity of the SMEFT Lagrangian that allows the construction of the SMEFT expansion,as laid out by other groups,and properties at that point of the Higgs-flare function F(h) coupling Goldstone and Higgs bosons,of the Higgs potential V(h) and of the Higgs-top quark coupling function G(h).

Keywords: SMEFT,HEFT,EFT,effective field theories,electroweak,LHC,quantum field theories

1.Introduction

Discovering new particles would entail the Standard Model(SM)being falsified in Popper’s sense[1]and force us to extend it.Absent such discovery,the SM is still falsifiable upon finding new forces among the known particles.Because the SM has a characteristic energy scale of 100 GeV (the mass of the Higgs boson at mh=125 GeV,as well as the vacuum constant v=246 GeV exemplify it),but no new particles below 1000 GeV have been found,there is a scale separation that begs the use of effective field theory.

The popular Standard Model effective field theory(SMEFT) extension of the SM electroweak symmetry breaking sector (EWSBS) adds operators classified by their mass dimension,

It is easy to ask oneself how the whole framework of SMEFT can be tested.Effective theories include all the possible interactions that are compatible with known particle content and the symmetries believed to hold.Would it not be that any separation from the SM could be recast in SMEFT form? In that case,absent some new light particle,any phenomena could be described by adding an operator with a parameter to the SM.This is not so,as we will detail.

The particle content of the electroweak symmetry breaking sector is packaged in a Higgs doublet field in the SM as in the SMEFT

where the Cartesian coordinates φacan be rearranged to thepolar decomposition in terms of the ωiGoldstone bosons(which set the orientation of H through the unitary matrix U(ω) and the radial coordinate hSMEFT(with ∣H∣=(v+hSMEFT).

Table 1.Correlations between the ai HEFT coefficients necessary for the SMEFT to exist,at order Λ-2(first and second columns,with the numbers in the second consistent with 95% confidence level experimental bounds a1/2 ∈[0.97,1.09] [21]).The right column provides the corresponding numerical values at the next order [5].They are quoted in terms of Δa1:=a1-2 and Δa2:=a2-1,so that all objects in the table vanish in the SM,with all the equalities becoming 0=0.

An additional non-linear redefinition of hSMEFTallows us to rearrange the SMEFT Lagrangian in the form of a more general theory,the Higgs effective field theory (HEFT):

Our current focus therein is the flare function [3,4]:

which amounts to a radial‘scale’(think of a(t)in a Friedmann-Robertson-Walker cosmology)in the field space of the(h,ωi) electroweak bosons (with ωianalogous to the spatial coordinates).What we call attention here is that the Taylorseries coefficients ofF as defined in equation(4)must satisfy experimental correlations or constraints as given in table 1 similar to the ones in[5]if the SMEFT is a valid description.3Our advance since our previous publication in [5] consists of the new correlations among the HEFT t quark-Yukawa sector coefficients,see equation(19)and the improvements to the correlations among the Higgs selfinteraction presented in equation (18) due to the cH□operator.The results presented here have been reported to the Quark Confinement and the Hadron Spectrum conference resulting in a preliminary publication [6].It is clear that an experimental program aimed at these correlations via the key process to accessF,ωω →nh as sketched in figure 1,mh →nh to access V(hHEFT) (the Higgs potential),ort¯t→nhto access the tree-level function modifying the Yukawa couplings,see equation (7),G(h),can test the validity of the SMEFT itself and not only its parameters.As an example,the SMEFT correlation among a1and a2is shown in figure 2.

Fig.1.The ωω →nh processes can be the key to disentangling the nature of the EWSBS.They give direct access to the ai coefficients of the flare functionF and hence to their correlations,as listed in table 1.Current experimental constraints do not really extend beyond n=2 and it will be challenging to examine higher coefficients.Better reconstruction techniques at the high-luminosity LHC run but especially a future high-energy collider (either hadronic or muonic)will hopefully improve the situation.

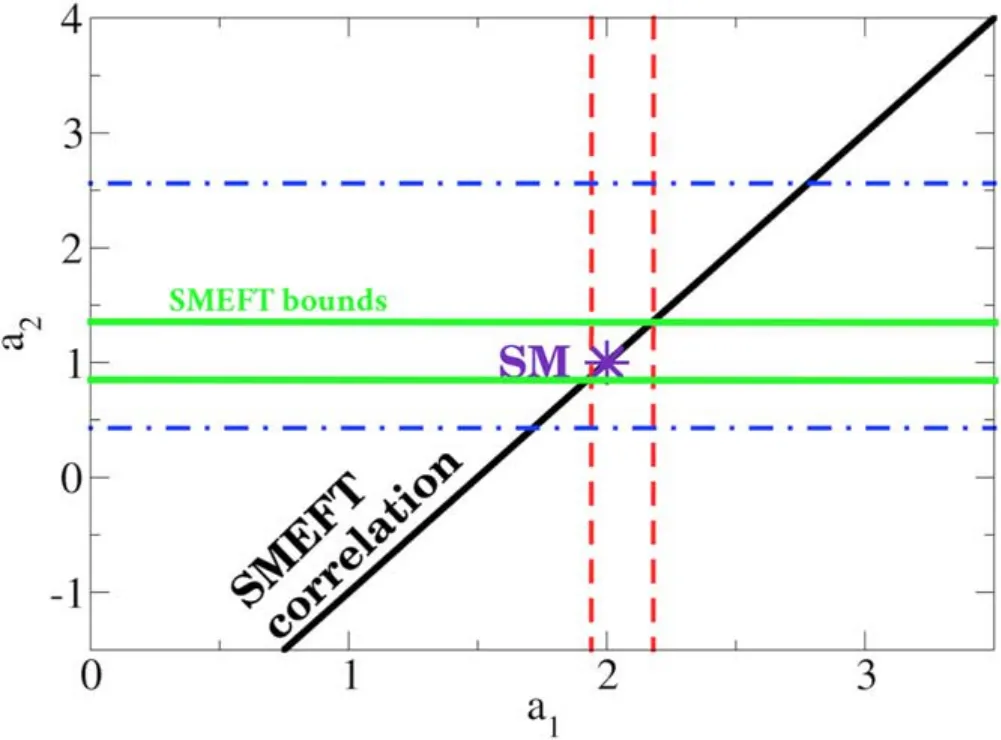
Fig.2.The correlation a2=2a1-3 that the SMEFT predicts at order 1/Λ2 is plotted against the current 95% confidence intervals for these two HEFT parameters [21,22].The dashed blue lines correspond to the direct experimental bounds prior to this work,while the solid green lines represent the bounds in table 1 coming from our 1/Λ2 correlation analysis.

There are several reasons why the experimental tests of those correlations need large energies and statistics,at the limit of what is possible today at the Large Hadron Collider(LHC) and beyond.First,theF function multiplies terms with derivatives of the Goldstone bosons ∂μωi→qμωithat yield couplings proportional to their four momenta and become more relevant at higher energies.Second,the equivalence theorem [7,8] tells us that the scattering of longitudinal gauge bosons is related to scattering of Goldstone bosons(ωi～,ZL): the EW gauging of the HEFT Lagrangian(3) leads to the WW →nh interaction

which for longitudinal gauge bosons clearly dominates over the non-derivative interactions from V only at high energies[9,10].Third,an increasing number of Higgs bosons(necessary to access each hnorder ofF,the Higgs-flarefunction) requires an ample phase space and,thus,high energy.

Table 2.Correlations among the coefficients Δv3:=v3-1,Δv4:=v4-1/4,v5 and v6 of the HEFT Higgs potential expansion in equation (6) that need to hold,at O(1Λ2),if the SMEFT is a valid description of the electroweak sector.Based on the current bound Δv3 ∈[-2.5,5.7] in Ref.[23],O(1 Λ2),the SMEFT predicts the coefficient intervals in the last column,testable in few-Higgs final states.A coupling cH□≠0 induces the correction Δa1 ∝cH□,nevertheless numerically negligible since v3 experimental uncertainties much exceed those of a1.Likewise,we include the leading correlations for the Yukawa G(h) function of equation (8),constraining c2 and c3 by c1 and a1(from the correction to the value of the symmetric point h*).We make use of current 95%confidence interval for the top Yukawa coupling c1 ∈[0.84,1.22] [24].

Table 2.Correlations among the coefficients Δv3:=v3-1,Δv4:=v4-1/4,v5 and v6 of the HEFT Higgs potential expansion in equation (6) that need to hold,at O(1Λ2),if the SMEFT is a valid description of the electroweak sector.Based on the current bound Δv3 ∈[-2.5,5.7] in Ref.[23],O(1 Λ2),the SMEFT predicts the coefficient intervals in the last column,testable in few-Higgs final states.A coupling cH□≠0 induces the correction Δa1 ∝cH□,nevertheless numerically negligible since v3 experimental uncertainties much exceed those of a1.Likewise,we include the leading correlations for the Yukawa G(h) function of equation (8),constraining c2 and c3 by c1 and a1(from the correction to the value of the symmetric point h*).We make use of current 95%confidence interval for the top Yukawa coupling c1 ∈[0.84,1.22] [24].

2.Correlations in HEFT parameters induced by assuming the SMEFT’s validity

As we show after equation (12),the correlations mentioned above arise from the need for consistency of the SMEFT formulation when a change of variable hHEFT→hSMEFTis performed.This change affects any other piece of the Lagrangian involving the Higgs bosons,such as the Yukawa couplings to fermions,saliently the top quark,or the interactions among Higgs bosons themselves (both of which we examine here),as well as couplings to transversal gauge bosons (that we leave for future works).

The much-discussed V(H) Higgs potential,experimentally accessible at ‘low’because it contains no derivative couplings,

acquires in the HEFT additional non-renormalizable couplings organized in a power-series expansion

with v3=1,v4=1/4 and vn≥5=0 in the SM.Its coefficients also need to satisfy constraints that are exposed in table 2 and figure 3 if and when the SMEFT applies.

Similarly,the SM piece coupling the top quark to the Higgs boson is extended in the HEFT[11]by a multiplicative functionG(h)

with a Taylor expansion around the physical h=0 vacuum given by

(with c1=1,ci≥2=0 in the SM).The correlations among these coefficients induced by the SMEFT at order 1/Λ2are then again given in table 2 and figure 4.

Let us then see,very briefly,how the various correlations come about.Instead of relying on the powerful geometric methods of [3,12—15],we use the more pedestrian coordinate-dependent approach,more familiar to phenomenologists working on LHC physics.The goal is to see when is it possible to cast equation (3) into the specific SMEFT one,equation (1).This we write as

where the non-derivative and derivative terms,respectively given by V and B,collect typical SMEFT operators (think of them as expressed in the Warsaw basis).Note that we have only kept the partial derivative part of the SM Higgs doublet kinetic term |DH|2in the right-hand side of equation(9),as we are considering the equivalence theorem and focused on the scalar sector of the theory.At the lowest order correction,1/Λ2,the relevant dimension-six SMEFT operators for our analysis are

There are also other operators,such as,e.g.OHD=(H†Dμ H)*(H†D μH),but they break custodial symmetry,and Large Electron—Positron Collider studies suggest that the SU(2)×SU(2)→SU(2) electroweak symmetry breaking mechanism is the appropriate pattern,leaving the residual custodial SU(2) as a good approximate global symmetry of the scalar sector.The additional A(H) structure pointed out in [16]for Lagrangian(9) can be eliminated through partial integration and the use of the equations of motion [5].

To proceed,we need to perform the following conversion to pass from the SMEFT to the HEFT and vice versa:

The change from the SMEFT to the HEFT is straightforward and always possible,with the canonical,non-linear change of variables given in differential form as

where the flare function is provided by the relation

However,the reverse conversion from the HEFT to the SMEFT,

runs into difficulty.This is because of the need to reconstruct squared operators of the Higgs doublet field H that is the basis of the SMEFT,such as

The extra |H|2on the right-hand side of the second equation ends in a denominator

As the SMEFT is assumed to have the analytical power expansion in equation (1),such singularity precludes its existence and needs to be cancelled by the preceding bracket in the second line of equation (16).

The result is the same as that obtained by geometric methods [16];there must be a double zero ofF and a symmetric point with respect to the global SU(2)×SU(2) group so that the SMEFT expansion can be performed.Furthermore,analyticity requires that all its odd derivatives vanish at the symmetric point.

The particular case of the SM is given by F=(1+hSMEFTv)2.As already pointed out,at higher orders in h/v,the existence of the SMEFT requires that the odd derivatives ofF at the symmetric point h* vanish.

The correlations from table 1 can then be obtained by matching the Taylor expansion ofF around such symmetric point hHEFT=h* with the expansion around our physical vacuum hHEFT=0.Instead of that matching,one can also obtain the correlations by eliminating the SMEFT Wilson coefficients order-by-order.For example,at O(1Λ2),there is only one operator,HO□,in equation(10),that controls all the HEFT coefficients ofF:

The elimination,by substitution,of this cH□coefficient from the HEFT ais yields the 1/Λ2correlations of the second column of table 1.Proceeding to the next 1/Λ4order in the SMEFT expansion brings in the Wilson coefficientHence,one can likewise extract the weaker 1/Λ4correlations among the HEFT parameters.The potential V(hHEFT) is in turn also affected byHO,

Also,the ciinG(hHEFT) modifying the Yukawa coupling receive analogous contributions from both SMEFT coefficients cH□and cuHin standard notation,the second alternatively namedctH+in [17].The correction

can be carried on to the higher coefficients using the relations in table 2 (with Δa1=2cH□vΛ2+O(1Λ4)).

3.Conclusions

Various authors,see e.g.[18],have pointed out differences between the SMEFT and HEFT formulations [19].For example,in the SMEFT the Goldstone ωiand Higgs hSMEFTbosons are arranged in a left-SU(2)doublet while in the HEFT hHEFTis an SU(2)⊗SU(2) singlet,independent of the Goldstone triplet ωi.In addition,in the SMEFT,the Higgs field always appears in the combination (hSMEFT+v) and,thus,the HEFT deploys more independent higher-dimension effective operators (in exchange,it is less model-dependent).This means that the SMEFT is natural when hSMEFTis a fundamental field while the HEFT is typical for composite models of the EWSBS (such as those with hHEFTas a Goldstone boson).Finally,the counting of the SMEFT is based in a cutoff Λ expansion taking the canonical operator dimensions,O(d)Λd-4(independently of Nloops),whereas the HEFT is a derivative expansion (independently of Nparticles) like the older electroweak chiral Lagrangian,with F(h) inserted in the derivative Goldstone term.

Nevertheless,a lot of this is cosmetic and can be reorganized by changing variables hSMEFT↔hHEFT.What is key is the San Diego criterion[3,12]:F(hHEFT)must have a point h*symmetric under the global SU(2)×SU(2)group and,due to its existence and convergence in the h field space,the SMEFT is deployable if and only if (which is a statement about the HEFT Lagrangian)

·∃h*∈ R where F(h*)=0,and

·because of the need for LSMEFTanalyticity,F is analytic between our vacuum h=0 and h*,particularly around h*.Moreover its odd derivatives vanish.We have presented new relations that implement this criterion at O(1Λ2)and O(1Λ4)in the 1/Λ counting;more precision is unnecessary until (if) separations from the SM are found.Then only with the scale Λ at hand out of separations of effective field theory coefficients from the SM can we decide how relevant the corrections due to the higher orders are expected to be and whether further work is warranted.

Among the three types of correlations that we have presented in tables 1 and 2,those for the coefficients ofF are more interesting for large values of the energy≫mh～mW～mZ,whereas those for V andG,that do not involve Goldstone bosons,are therefore of greater interest at low energies,when the potential competes with the derivative operators on equal ground,as～mi.

In conclusion,we have newly translated these conditions into correlations among HEFT coefficients whose violation falsifies the SMEFT.Moreover,since many extensions of the SM incorporating supersymmetry,supergravity or other possibilities can be cast as an SMEFT,they can be likewise simultaneously falsified.

For the time being,no separations from the SM have been found [20] and one can only infer direct experimental bounds on the first terms,a1and,perhaps,a2,so we have to wait for data with a larger number of Higgs bosons before assessing them.However,when this is done,the correlations will allow us to falsify the SMEFT in experiments even without new particles.We believe that this possibility improves the standing of the SMEFT as a scientific theory.

Acknowledgments

Supported by Spanish MICINN PID2019-108655GB-I00/AEI/10.13039/501100011033 grant,and Universidad Complutense de Madrid under research group 910309 and the IPARCOS institute;ERC Starting Grant REINVENT- 714788;UCM CT42/18-CT43/18;the Fondazione Cariplo and Regione Lombardia,grant 2017-2070: and by Grant DataSMEFT23 (EUNextGeneration—PNRR—DM 247 08/22).