基于水翼艇的现代控制理论实验设计

王端松，杜成涛，张 坦，张金仲

（皖西学院电气与光电工程学院，安徽 六安 237012）

1 前言

现代控制理论作为一门科学技术，已经广泛地运用于我们社会生活的方方面面，如航空航天、海洋领域和工业机器人等领域。现代控制理论的实验教学是理工科院校重要的教学环节[1]，然而，在现代控制理论实验教学领域，面临着如下问题：控制技术在近二、三十年得到飞速发展，新理论和新的控制方法不断出现，内容包含大量的公式证明以及矩阵的运算，理论较强且比较抽象，如果不与实际的物理系统相结合，非常难以理解，学习难度较大。以往的教学实验大多属于演示性或验证性实验，与实际工程结合不紧密，变量的值虽然能随意改变，但是意义单一，学生做实验做完就忘，限制了学生动手能力和创新能力的培养。因此，有必要在实验课程的教学中引入实际物理系统，将理论知识赋予物理意义，帮助学生更好地理解和掌握现代控制的理论知识。

虽然在现代控制理论的实验教学中有专家学者引入了能控性、能观性、极点配置的实验，并且通过MATLAB 编程进行仿真，但是各模块的仿真实验很多都是独立的，不能系统地联系在一起，使得知识点碎片化，仍然无法使学生获得真实且直观的感受。为此，南京邮电大学的丁洁等人设计了基于飞控平台的现代控制理论综合实验[2],包括飞行器的数学模型建立、状态观测器设计和跟踪控制实验。张勇[3]教学团队以倒立摆平台作为载体，通过对倒立摆进行数学建模、稳定性分析、能控性判断和极点配置等设计了综合实验，改变了传统的教学模式，取得了一定的教学实践效果。南京航空航天大学张苗[4]教学团队以直流电机为例，进行实验课程探索，从控制系统建模到模型线性化、状态空间表达式建立、能控性和能观性分析、状态反馈和状态观测器设计，将理论知识和实践更好地结合在一起，很好地改善了实验课程的教学效果。邢景虎[5]教学团队为了解决现代控制理论教学实验中学生学习积极性不高、理论性较强的问题，设计了基于单级倒立摆的仿真及实物实验，取得了良好的教学效果。

受以上文献启发，本文针对现代控制理论实验教学领域的不足，拟结合笔者的科研经验，探索基于水翼艇的现代控制理论综合实验设计。本实验侧重于理论结合实际，从工程角度理解理论知识，培养学生分析问题、解决问题以及学以致用的能力，可以有效激发学生的学习兴趣，培养学生的研究能力和创新精神。

2 水翼艇状态空间建模

笔者在现代控制理论实验课程的教学过程中，以美国的PCH 水翼艇作为教学案例，从系统数学模型建立出发，并转化为状态空间表达式分析系统的性能。

船舶在水面上为六自由度运动，分为沿x轴的纵荡运动、沿y轴的横荡运动、沿z轴的垂荡运动，对应的纵向速度、横向速度和垂向速度分别用u，v，w表示，以及横摇、纵摇、艏摇（分别关于x，y，z轴的角运动），对应的角速度分别用p，q，r表示，如图1 所示。

图1 水翼艇固定-随体坐标系示意图

水翼艇运动较为稳定的条件下，可以看作是在平衡点附近的微扰运动。PCH 水翼艇纵向运动的线性化方程为[6]：

其中，h表示垂荡位移，θ为纵摇角度，δe和δf分别表示水翼艇的艏翼角度和尾翼角度。Zs和Ms为干扰量。为了方便，在本文中假设外部环境干扰为0，即Zs=Ms=0。水翼艇的纵向运动状态纵摇角度和垂荡位移通过控制艏翼角和尾翼角来改变，当控制输入和外部干扰为零的情况下，如果初始状态不稳定，水翼艇会由给定的初始状态进行纵向运动，能量逐渐衰减到静止的平衡状态。

根据水翼艇的纵向运动线性化方程，水翼艇的数学模型使用状态空间表达式可以表示为：

通过MATLAB 指令eig(A)可以求出，此时闭环系统的特征值为-9.8594，-4.7731，0.009±0.8441i，从特征值可以看出，由于具有正实部的特征根，所以系统此时是不稳定的。此时如果设置水翼艇的初始状态为垂荡位移h=1.5m，纵摇角θ=5°，输入u=[0 0]T，通过搭建simulink 仿真程序，可以得到水翼艇的运动状态曲线，在没有控制输入和环境干扰的条件下，水翼艇垂荡位移和纵摇角运动曲线为正弦震荡，不能由给定的初始状态衰减到稳定状态，所以系统不能收敛，也验证了系统的不稳定性。

3 水翼艇状态反馈实验设计

3.1 状态反馈

状态反馈是将系统的每一个状态变量乘以相应的反馈系数，然后反馈到输入端与参考输入相加形成控制律，作为受控系统的输入[7]。

对于由状态空间表达式（2）表示的受控系统，状态线性反馈控制律u为[8]：

其中，v为r×1 维参考输入，K为r×n维状态反馈增益阵。

把方程（3）带入（2）可得状态反馈闭环系统的状态空间表达式为：

可以简记为：∑K((A+BK),B,C)。

3.2 极点配置

极点配置问题就是选择合适的状态反馈矩阵，将闭环系统的极点配置在根平面期望的位置上，来获得期望的动态性能。为了实现对水翼艇纵向运动的控制，需要对系统进行极点配置，保证闭环系统是稳定的[9]。

设置水翼艇纵向运动系统的期望特征值为λ1,2=-3±3j,λ3=-5,λ4=-6，可以看出，一对共轭复根为系统的主导极点。

首先，可以通过MATLAB 对水翼艇的能控性和能观性进行验证。该系统的可控性矩阵秩为4，即rank(B,AB,A2B)=4，能观性矩阵秩rank[CT(CA)T(CA2)T(CA3)T]T=4，所以闭环系统是完全能控且能观的，可以通过状态反馈对系统进行极点配置。

用MATLAB 编程求取系统的状态反馈增益阵K：

此时如果设置水翼艇的初始状态为垂荡位移h=1.5m，纵摇角θ=5°，输入u=[0 0]T，水翼艇的运动状态曲线如图2 所示。状态空间1 和2 分别为垂荡位移和纵摇角，从图中可以看出，在执行机构没有动作的情况下，水翼艇的垂荡位移和纵摇角运动曲线由初始状态经过短暂的调整分别到达平衡点，其导数值也达到平衡点，证明了极点配置的有效性。

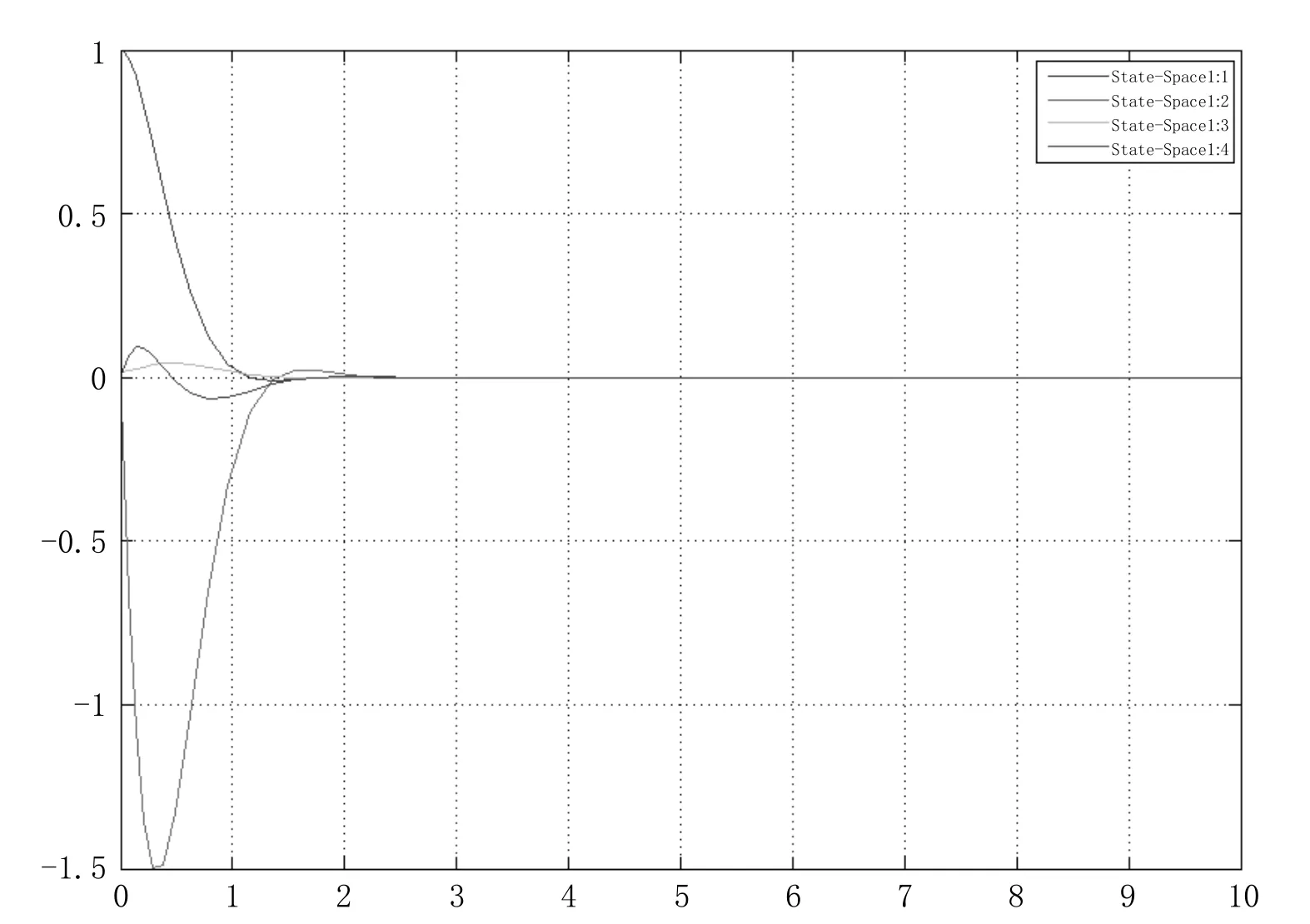
图2 水翼艇纵向运动状态反馈的状态响应曲线

4 结语

本文通过对水翼艇的纵向运动方程进行建模，进而转化为状态空间表达式，通过判断求取系统的极点，由极点的分布情况判断系统的稳定性。然后，通过设计状态反馈增益阵实现对水翼艇纵向运动系统的极点配置，保证闭环系统的稳定性。通过MATLAB 仿真证明了有效性。