小水电智能微电网可靠性分析

邢智博，任家智，辛 鑫，王永垚，刘子源

（山西能源学院，山西 太原 030001）

近些年，环境污染、能源稀缺等问题日益严峻，如何充分利用清洁能源成为业内人士研究的重点，智能微电网的出现，使能源利用率得到了大幅提高。作为由微电网、智能电网组合而成的全新电力系统，智能微电网可兼具孤岛及并网模式，这也决定其可以对风能和光伏等常见能源进行充分利用。若将其用于偏远地区，可以有效控制铺设电缆的规模，降低项目投资费用；将其应用于城镇地区，则能够通过减轻用电负荷的方式，提升大电网稳定性。

1 研究背景

本文所研究微电网系统由小水电系统、光伏发电系统、风力发电系统及蓄电池等部分组成，系统作为独立电网运行，不考虑与电网接入情况。在运行过程中，通常需要经由上述构件控制频率电压并提供无功/有功功率，这也决定了一旦设备出现故障，便有较大概率造成负荷停电。目前，可能造成负荷停电的情形主要包括以下几种：首先是分布式电源出现故障，故障发生后，通常需要花费数小时或是数天进行维修，方可恢复正常。其次是电源受故障影响而跳机，此时，需要工作人员重启电源，重启前，重要负荷始终处于停电状态，自动重启的用时通常为数秒，手动重启的用时则会达到数小时。最后是由于电压跌落或是其他电能质量问题，致使设备调机。研究发现，开关动作、闪点以及故障均会造成电压跌落，若分布式电源所接入负荷较多，则需要频繁开关，供电可靠性也会受到影响[1]。

2 可靠性分析内容

微电网的本质是由负荷、分布能源和储能装置共同组成的发配电系统，智能电网则具有与供电网路相同的作用，即：以既有传感器为依托，实时收集设备参数，向控制系统下达相应指令，由此达到对电力系统进行科学管理的目的[2]。因此，对微电网可靠性进行分析势在必行。可靠性分析主要涉及两方面内容，分别是安全性、充裕度，这两方面内容对微电网长期可靠供电有巨大影响，对常规配电系统进行分析能够发现，虽然可以影响系统可靠性的因素较多，但充裕度所带来影响明显强于其他因素，任一元件出现故障，均会造成供电中断，进而对用户工作或是生活产生影响。对本文所讨论的智能微电网而言，其所表现出的可靠性主要取决于互联系统，要想使系统得到稳定、可靠的运行，关键是要对动态问题进行深入分析，根据分布式电源的性能，评估系统可靠性。为保证分析所得出结论具有实际意义，在仿真分析中引入负荷数据、等效动态模型，基于此类方法，保证分析结果具有实际意义。

3 可靠性分析过程及结果

本文所讨论微电网由小水电、光伏和储能等部分组成，对其可靠性加以评估所考虑要素见图1。

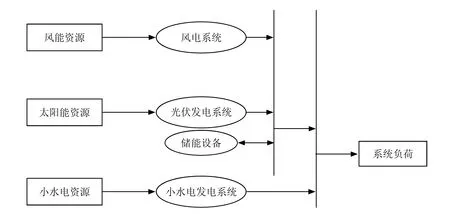
图1 可靠性评估要素

本文主要分析微电网独立运行情况，小水电系统在其中作用主要体现在两个方面：一是为微电网持续供电；二是对储能电站进行协调，使电力负荷和发电系统始终处于供需平衡的状态[3]。

3.1 分析过程

3.1.1 建立模型

首先是小水电模型。实践经验表明，导致小水电停运的原因有两个，分别是机组存在故障、水位高度不满足要求，基于以上两个原因建立相应模型。若将水轮机所搭载机组数量设定为n，将任一机组出现停运事故的概率设定为r，可以得到模型如下：

该模型中，k代表停运机组总数；Pk代表累计停运概率。在0～1 范围内随机抽取多组数据，对比所抽取数据和累计停运概率，则能够准确掌握既有机组的状态、可稳定运行的机组数量，随后，再以系统针对机组运行情况、小水电出力情况所提出要求为依据，参考状态持续时长完成抽样，便可以对小水电出力加以确定。

其次是装置模型。评估光伏、储能和风电可靠性的模型首选两态模型，其构成见图2：

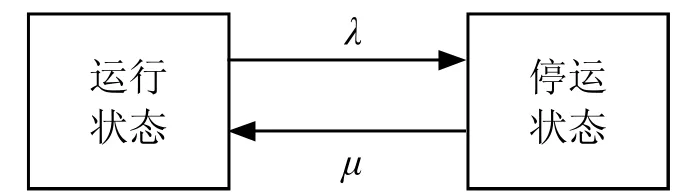
图2 两态模型

图2 中，μ代表修复转移率；λ代表故障转移率。基于蒙特卡罗法，快速确定MTTF、MTTR取值[4]。考虑到状态持续时长对应抽样值具有指数分布特征，因此，可使用下列公式推算系统修复时长、无故障时长：

在上述公式中，MTTF代表无故障时长平均值；MTTR代表修复时长平均值；TTF代表无故障时长；TTR代表修复时长；U及U'均为随机数，取值范围是0～1。确定各项参数的取值后，便可以对强迫停运率进行计算，相关公式如下：

该公式中，FOR代表强迫停运率。

最后是可靠性模型。研究中，根据时序负荷情况建立了相应的模型，简单来说，就是在年负荷最大值确定的前提下，使用百分数描述日负荷、周负荷的最大值。上述工作结束后，便可以得到系统负荷情况。

系统全年负荷峰值假定出现在51 周，如果将冬季作为一年的开端，冬季负荷明显高于其他季节，如果将夏季作为一年的开端，则代表夏季负荷高于其他季节。要想快速、准确地计算出负荷期望值，建立以下表达式，即：

在该表达式中，Plst(t)代表负荷期望值。Plmax代表年负荷最大值。Pweek(t)代表周负荷最大值与年负荷最大值之比。Pday(t)代表日负荷最大值与周负荷最大值之比。Phour(t)代表小时负荷最大值与日负荷最大值之比。

3.1.2 确定可靠性指标

对电力系统而言，其可靠性指标往往包括两类，分别是概率指标、确定性指标，其中，确定指标难以对系统状态进行全方位的表现，概率指标则不存在该问题[5]。

鉴于此，本文选择以系统、负荷为切入点，围绕可靠性指标展开讨论。

在正式展开研究之前，先将系统分成三层，第一层的评估对象是发电系统，可以简单理解为对电源可靠性进行评估，第二层是发输电系统，第三层是电力系统，本文研究的对象为微电网，因此，应当将重心放在发电系统上。在对多方面因素加以考虑后，最终确定LOEE、LOLE两大指标，二者的含义和计算公式如下：

上述公式中，LOEE代表电源发电量与负荷需求不符时微电网所期望的电量；ENSi代表各抽样年中均无法达到负荷需求的实际电量。LOLE代表微电网对电源与负荷需求不符时间的期望；LLDi代表各抽样年中存在电力不足问题的时长。随后，便可以充分利用评估指标、已建立模型，对微电网各部分状态进行判断，结合时序模拟分析所得到结果，确定微电网性能、既有负荷点是否可靠。

3.1.3 评估微电网可靠性

在研究中，依据蒙特卡罗法分析系统可靠性，以小时为单位，记录系统电源运行参数、负荷变化情况。模拟总时长是365 天，时间的间隔是1h，具体流程如下：

第一步，以年为单位，获取小水电、光伏以及负荷的相关数据，生成相应的出力时序。

第二步，以既有模型为基础，使用现有公式推算电源的状态时序。

第三步，根据状态时序、出力时序，对功率输出时序加以确定。

第四步，对比负荷需求、电源出力情况，对LOEE、LOLE取值进行计算，参考相应的经济指标，得出最终结论。

3.2 分析结果

3.2.1 负荷峰值与可靠性的关系

本文所研究智能微电网搭载有相应的发电系统，系统可靠性极易被负荷波动所影响。对负荷峰值、系统可靠性之间的关系进行分析，能够准确掌握系统所能承受负荷的最大值，便于工作人员以微电网所展示出状态为依据，对后续运行方案及策略加以调整，使发电系统以及微电网始终处于稳定、高效的运行状态。研究发现，负荷峰值在60kW 以下时，各项可靠性指标相对稳定，这表示发电系统与负荷需求相符，负荷峰值超过60kW后，各项指标均会发生明显的变化，换言之，要想使系统得到稳定且高效的运行，关键是要保证负荷值不超过60kW。

3.2.2 水库容量与可靠性的关系

基于评估可靠性的模型模拟微电网所搭载电力系统，可以得到以下数据：

首先，每组水电机组的容量都是30MW。

其次，水库原始水量能够达到其容量的95%～97%。

最后，结合某地所提供统计数据可知，水体径流量的平均值在0.32m³/s 左右，由此可见，水流量与水电机组所提出需求相符，这表示水流量可以维持水电机组稳定运行。

随后，围绕水库容积、系统可靠性之间的关系展开研究。通过模拟不同容积的水库，判断容积对可靠性指标所产生的影响。经过分析发现，在负荷确定、上游水量确定的前提下，水库蓄水量会随着容积的增大而增多，与此同时，LOEE、LOLE 的取值均会有所下降。水库容 积增大到15 万m3后，蓄水量差值将处于相对稳定的状态，LOEE、LOLE 的下降速度有所减慢，并逐渐趋于平缓，同时既有水资源的利用率也较以往有所提高。由此可见，对本项目而言，要想使系统具有良好的可靠性，关键是要将水库容积控制在约15 万m3。

4 结论

综上，本文分别对储能、小水电、风电以及光伏模型进行了模型建立，根据电源所展示出运行状态，围绕峰值负荷、水库容积与系统可靠性之间的关系展开了讨论。现将研究所得结论归纳如下：其一，峰值负荷与系统可靠性密切相关，要想使本系统得到稳定运行，应保证峰值负荷始终不超过60kW。其二，水库容积同样会对系统可靠性产生影响，酌情增大水库容积，既能够使系统更加可靠，又可以为项目所具有的经济价值提供保证，但要注意一点，若是水库容积增大过多，将会对可靠性造成负面影响。