基于Prophet模型的省级关口计量装置异常判断方法

林彤尧 黄天富 吴志武 王春光 黄汉斌 涂彦昭

(国网福建省电力公司营销服务中心,福建 福州 350000)

*通信作者:林彤尧,E-mail:tongyao_lin@163.com。

0 引言

关口计量装置是准确计量发、输、用各方电能的关键设备,对购、售电客户之间公平考核和决算电量起重要作用[1-2]。计量装置的计量准确性直接关系着各方经济效益[3],研判关口计量装置运行状态是电力营销的重点工作之一。

判断关口计量装置运行状态的传统方法是利用人工对装置进行实地周期巡检,需要大量人力和物力[4]。然而,随着电网规模不断扩大,关口计量设备不断增多,人工巡检的方式已然不能满足监测关口计量装置运行状态的需求。因此,涌现出多种关口计量装置在线监测方法来实现远程研判计量装置状态[1,5-6]。高利明等[1]使用GPS技术和低压宽带载波通信技术实时采集关口电能表和电压、电流互感器二次回路信号,利用机器学习算法分析时空维度特征,实现远程在线异常研判;申莉等[5]采用GPS同步采样和无线通信技术的高精度采样远程获取电力数据,并通过故障诊断模型进行状态分析;徐严军等[6]从14个特征中通过无监督的预训练和有监督微调构建深度学习模型,自动学习关口异常特征。但是,上述方法需要大量基础数据进行特征分析,在部分实际应用场景无法使用。这是由于在当前复杂的信息化背景下,发电厂、变电站的电力数据易被不法分子盯上,为保障信息安全,部分网省公司对变电站电压、电流、电量数据实行保护,计量系统无法直接获取电压、电流、功率因数等运行数据,仅能获得电量数据,数据特征较少,给远程研判带来了极大的挑战。

为了解决上述难点,本文提出了一种能适用各类关口场景,并且仅使用电量数据便能远程研判关口计量装置异常的方法。该方法基于能量守恒定律与Prophet预测方法,以厂站内主变、母线或输电线路为监测单元,通过计量点的历史输入、输出电量得到关口的损耗曲线,接着使用Prophet模型对关口的近4个月历史损耗曲线进行拟合,预测出其未来1个月的损耗率,并根据未来损耗率的95%置信区间设定损耗阈值。当实际损耗超出损耗阈值时,及时发出预警,由人工进行复核分析关口计量装置是否处于异常状态,并定位故障计量点[7]。

1 问题分析

由于部分变电站实行电力数据分区保护,计量系统只能获得关口的电量数据。为能远程监测关口计量装置的运行状态,目前采用电量平衡法进行监测,即通过关口的输入和输出电量数据得到对应的损耗率曲线,随后人工观察该曲线是否存在突变进,从而研判计量装置的运行状态。但由于部分关口曲线频繁波动,人工观察很容易误判计量装置运行状态。图1为某两个变电站1#主变某一时段的损耗率。

由图1可知,A变电站主变损耗率一直为正损且波动幅度较小,监测人员很容易判断关口运行状态是否正常;而B变电站主变受综合倍率和采集精度的影响,损耗率出现正损和负损交替且频繁波动的情况,监测人员难以分辨损耗率波动是系统误差,还是由计量装置异常产生。针对上述问题,本文将探索Prophet阈值预测方法,预测关口损耗率的波动范围与规律,提出仅依靠电量数据便能高准确率识别关口计量异常监测的新方法。

(a)A变电站1#主变 (a)B变电站1#主变

2 算法原理与方法流程

2.1 Prophet预测原理

Prophet预测算法的原理是基于时间序列分解和机器学习拟合,该算法能够快速得到未来的预测结果,并能自动处理数据的异常值与缺失值,减少人工对数据集的预处理步骤。

该算法模型为3个关于时间t的函数和误差项εt相加,时间函数分别包含趋势函数g(t)、周期函数s(t)和节假日函数h(t),通过数据拟合函数,得到时间预测序列,其公式为:

y(t)=g(t)+s(t)+h(t)+εt

(1)

式(1)中,g(t)为趋势函数,表示时间序列在非周期变化的趋势;s(t)为周期函数,可表示以周、月、季节或年周期变化的趋势;h(t)为节假日函数,表示节假日影响量;ɛt为误差项。

Prophet模型中,趋势函数g(t)是基于传统逻辑回归模型的趋势项,将逻辑回归模型中的固定参数替换为随时间变化的函数,并加入时间变点,以适应潜在的非周期变化趋势,其公式为:

(2)

式(2)中,C(t)表示模型容量;m表示为偏移参数;q表示增长率。

其中,a(t)=(a1(t),a2(t),…,ad(t))T

δ=(δ1,δ2,…,δd)T

(3)

γ=(γ1,γ2,…,γd)T

式(3)中,a(t)为增长率变化量参数;δ为增长率变化量;γ为时间变点函数;d为时间变点的个数。

Prophet模型中周期函数s(t)是通过正弦余弦函数来表示周期的变化,为了更好地达到拟合效果,使用傅里叶级数来拟合周期性,其公式为:

(4)

式(4)中,β为周期变化参数,初始为高斯分布,控制周期效应的强弱;an、bn为傅里叶级数展开项系数;P为时间序列的周期,若P=30,则表明以月为单位的周期变化,若P=90,则表明以季度为单位的周期变化。

Prophet模型中节假日函数h(t)是通过设定特殊的时间节点,同样使用变化参数,达到节假日影响前后一段时间的时间序列的效果,其公式为:

h(t)=Z(t)×μ

(5)

式(5)中,t为自行设定的节假日时间节点;μ为节假日参数,初始为高斯分布,控制节假日效应的强弱。

2.2 基于Prophet的省级关口计量装置异常判断方法

本文提出的计量关口异常判断方法的流程如图2所示。首先,需要获取每个关口电量历史数据,并计算得到对应的损耗率Dt={dt1,dt1,…,dtN};再根据全省关口电量的节假日特性、周期性,设置对应Prophet模型参数。接着,使用Prophet模型对每个关口的未来损耗率作出预测,并设置置信区间95%得到损耗阈值Et。若在此期间出现当天损耗率A1超出当天损耗阈值Et,则发出预警,由人工进行复核分析关口计量装置是否处于异常状态。

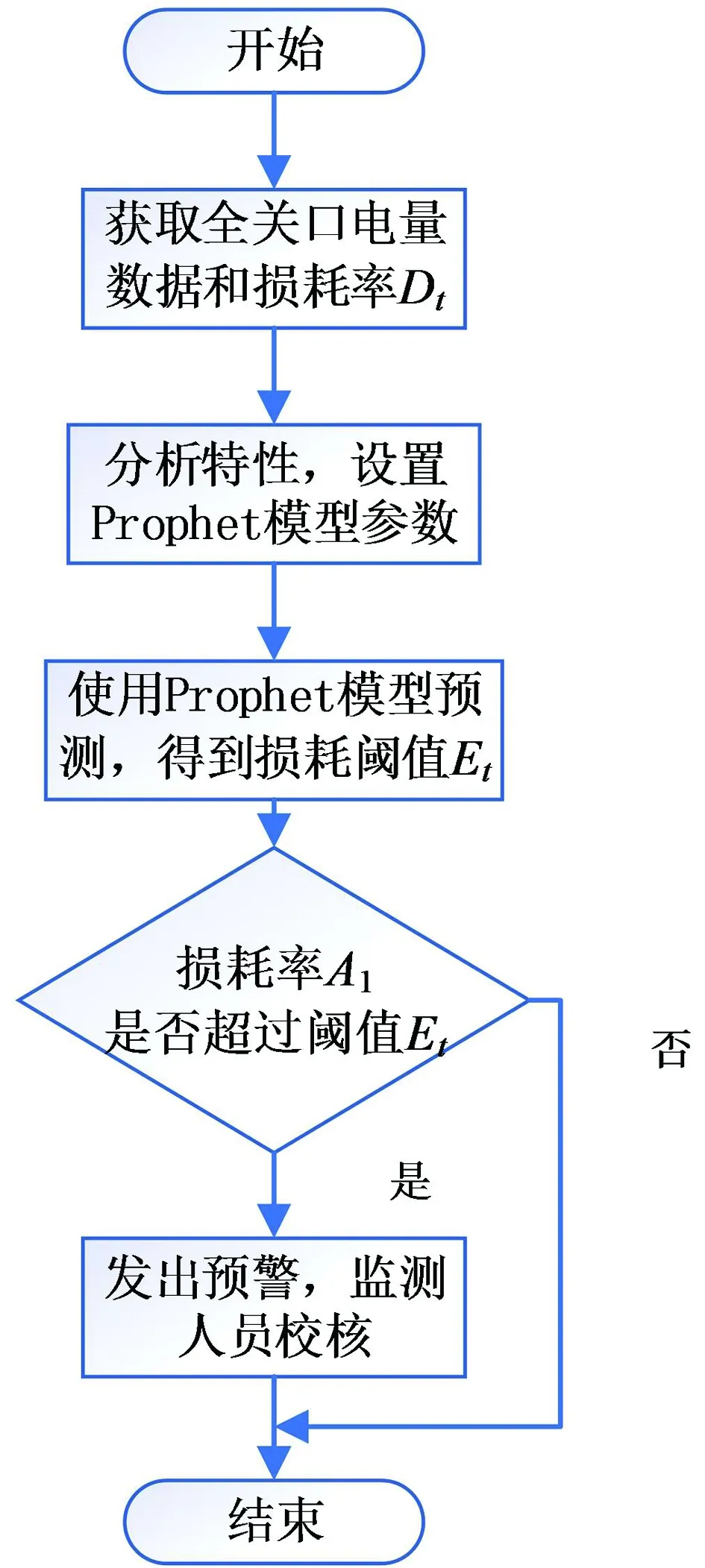
图2 基于Prophet的省级关口计量装置异常判断方法

在分析节假日特性、周期性步骤中,由于Prophet模型分别是用高斯分布和傅里叶级数拟合节假日特性和周期性,因此需要通过关口电量数据Dt分析节假日的影响时间区间和关口损耗率的傅里叶特性,以便确认Prophet模型参数。

在使用Prophet模型预测步骤中,考虑到预测的准确性和实际应用情况,本文以30d为一个预测周期,每个监测单元利用近4个月历史损耗率来预测下一个周期阈值。

3 算例分析

3.1 实验参数设置与评价指标

文本实验的集成开发环境为PyCharm,Prophet模型的搭建通过fbprophet实现,系统运行环境为Windows 11,CPU为AMD Ryzen 7-5800H,使用的数据由某省的省级计量关口管理平台直接导出。在Prophet模型参数设置部分,节假日影响区间设为3d或1d,周期性设置为3d,并选择线性方式预测,变点影响数值设为默认值0.1,选择损耗阈值的置信度区间为95%。

本文使用召回率和精确度指标用于衡量模型性能。召回率表示实际为正样本的结果中,预测为正样本的比例,召回率越高,模型对故障应检尽检的效果越好,不易漏掉故障关口;精确度表示预测出来为正样本的结果中,实际为正样本的比例,精确度越高,模型判断故障关口的正确率越高,减少判断错误造成复核资源的浪费。

3.1.1 Prophet模型节假日参数

在设定Prophet模型节假日影响区间时,根据近三年关口全电量历史数据,得到3年内平均节假日期间全计量关口电量,如表1所示。

表1 节假日期间电量 单位:108kWh

由表1可知,除春节、国庆节外,计量关口电量均在节日前一天出现下降,在节日当天下降到最低,在节日后两天电量基本与节日前两天电量持平,假日影响范围区间较小。例如,五一节前两天电量为3.22×108kWh,前一天电量为3.19×108kWh,电量无明显变化,仅在五一节当天降至低点2.75×108kWh,随后电量开始爬升,节后两天的电量为3.12×108kWh,与节前两天电量基本持平。而春节与国庆节计量关口电量在节日后第四天才恢复到节前大小。综上所述,将三天节假日的影响时间区间设定为1d,将春节与国庆节的影响时间区间设定为3d。

3.1.2 Prophet模型周期性参数

在设定Prophet模型周期性时,本文对历史关口电量数据使用傅里叶变换方法,将时域数据转为频域观察,通过观察最大振幅的正弦波周期,确认周期性。为了便于展示,文章随机选择三个变电站计量点画出幅值归一化后的傅里叶频域图(图3)。由图3可知,三个计量点出现幅值高位均集中在2～3d,周期符合损耗率频繁波动的实际情况。因此,Prophet模型的周期性设置为3d。

图3 幅值归一化后的傅里叶频域图

3.2 Prophet模型预测实验

本文取每个监测单元5个月的历史损耗率,将其中前4个月历史损耗率作为训练集,用来预测后1个月的损耗率,并将预测损耗率与实际损耗率作对比。此外,为了验证Prophet模型的性能,本文使用其他预测方法对同样的数据进行预测,并进行效果对比。图4为4种不同方法预测某主变损耗的结果。

(a)Prophet预测模型(b)指数平滑预测模型

(c)LSTM预测模型(d)ARIMA预测模型

由图4可知,在预测准确率方面,指数平滑模型与LSTM模型将损耗率频繁上下波动现象识别成噪声,认为损耗率保持固定,因此,预测值为基本恒定值,无法跟随实际值损耗,起不到预测与预警的作用。而Prophet与ARIMA模型的预测值可以较好地跟随实际值,反映出损耗率的波动情况。在预警阈值上下限方面,LSTM模型的阈值上下限差值过小,指数平滑模型差值过大,均无法起到预警作用。在Prophet模型中,阈值差值适中,而ARIMA模型预测的阈值较为粗放,阈值面积超出Prophet模型阈值的50%以上,对关口异常损耗率不敏感,不易发现异常点。

综上所述,LSTM与指数平滑模型容易预测失败,ARIMA模型预测的阈值面积过大,容易漏检异常信息,Prophet模型虽然偶尔会误判状态,但能对异常信息应检尽检。因此,Prophet模型作为预测方法最为合适。

3.3 实验结果

为了进一步验证Prophet模型性能,取近3年内出现装置故障的关口损耗率曲线。为保证样本平衡,按1∶1比例加入正常运行的损耗率曲线,共计124条曲线。以故障日的前3个月曲线作为训练集,后1个月作为预测验证集,验证Prophet模型能否正确对故障日作出预警,能否对正常运行不误报,实验结果如表2所示。

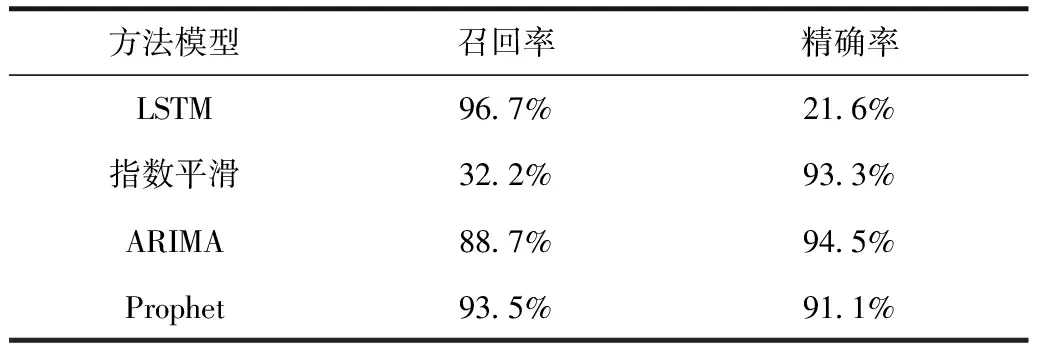
表2 关口计量装置异常计算结果

结果显示,Prophet模型在计量关口异常识别上有较高的召回率和精确率,分别达到了93.5%和91.1%,优于其他方法。

4 结束语

针对现有关口计量装置运行异常判断的问题,提出了一种基于Prophet模型的计量关口异常判断方法,结论如下:

①Prophet预测模型能适用于实行电力数据分区保护的变电站,仅依靠电量数据就能较好地预测出监测单元未来损耗阈值,相比于其他方法模型,有计算速度快、性能好、适用节假日和周期性的特点。

②通过省级计量平台导出的真实数据进行分析验证,Prophet模型在计量关口异常计算上的召回率与精确率分别为93.5%和91.1%,优于其他方法。