利用整体法巧解两道动力学难题

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

对于同一平面内相互作用的几个质点,无论各质点的加速度是否相同,都可选择整体为研究对象在某一方向应用牛顿第二定律列方程.特别是对于多个相互作用物体的相对运动问题,利用这种整体法来解答,可化繁为简,巧妙快捷.

1 推导系统牛顿第二定律的表达式

以相互作用的两个质点沿同一直线运动为例,设质点A和B的质量分别为m1和m2,在某一时刻的加速度分别为a1和a2,合外力大小为F,作用点在质点A上,相互作用力大小为f,若利用隔离法对各质点分别应用牛顿第二定律列方程,则有

F-f=m1a1f=m2a2

由两个方程相加得

F=m1a1+m2a2

可见,这个方程不含内力,是把相互作用的两个质点视为整体而列出的动力学方程.这表明,在同一直线上运动的两个质点受到的合外力,等于各质点的质量与对应加速度乘积的矢量和.

由于相互作用的内力是成对出现的,而且是互为相反数,因此对质点组利用整体法列出的动力学方程中不含有内力.对于方程右边的各项,分别对应合外力的一个分力,即

F1=m1a1F2=m2a2

下面利用质心坐标公式和质心运动定理推导质点组的系统牛顿第二定律表达式.对于平面直角坐标系内的质点组,系统质心的横坐标为

取二阶导数可得系统质心在x轴方向的加速度为

由质心运动定理可知在x轴方向的合外力为

Fx=(m1+m2+…+mi)aCx=

m1a1x+m2a2x+…+miaix

即

Fx=∑miaix

这表明,对于做变速运动的各质点组成的整体,在某一方向受到的合外力等于各质点的质量与对应加速度分量之积的矢量和.无论各质点受到外力的作用点是否相同,力的作用线是否重合,各质点的加速度是否相同,各矢量是否共线,都可对质点组整体在某一方向应用牛顿第二定律列出一个动力学方程.

综上可见,对于平面质点组或者连接体在平面内发生的变速运动,都可对整体在某一方向上应用牛顿第二定律列出一个动力学方程,只与该方向的合外力有关,而与相互作用的内力无关.表达式的一般形式为

F=∑miai

2 应用系统牛顿第二定律的表达式

对有关质点组的动力学问题,常规解法是利用隔离法由牛顿第二定律列方程,显得很繁琐,且易于出错.而对质点组整体应用牛顿第二定律即利用系统牛顿第二定律列方程,实际是一种整体法,只需分析整体受到的外力以及各质点加速度的大小和方向,不必考虑相互作用的内力,由此可化繁为简,化难为易.

【例1】[1]系统如图1所示,滑轮与绳的质量忽略,绳不可伸长.设系统所有的部位都没有摩擦,物体B借助导轨(图中未画出)被限定在沿物体C的右侧面运动,已知物体A、B、C的质量分别为mA、mB、mC,试求物体C运动的加速度aC.

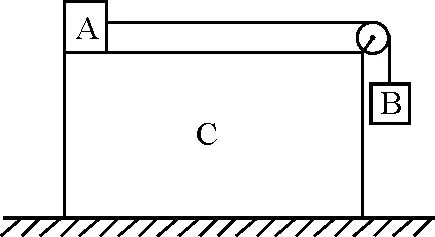
图1 例1题图

原解[1]:取物体系统为研究对象,由于A、B、C组成的系统在水平方向上动量守恒,则

mAvA=(mB+mC)vC

(1)

再隔离A和B,由于A和B相对于C的加速度大小相等,设为a,则A对地的加速度为aA=a-aC,方向向右;B对地的加速度可分解为两个分量,竖直向下的分量aBy=a,水平向左的分量aBx=aC.设绳的拉力为T,分析A水平方向和B竖直方向的受力情况,根据牛顿第二定律,对A有

T=mAaA

即

T=mA(a-aC)

(2)

对于B,在竖直方向有mBg-T=mBaBy,即

mBg-T=mBa

(3)

联立方程(2)、(3)得

(4)

又因为A、C均做初速度为零的匀加速直线运动,由速度公式得

vA=aAt=(a-aC)t

(5)

vC=aCt

(6)

联立方程(1)、(4)、(5)、(6)可得

点评:在惯性系中应用牛顿第二定律列方程,要注意加速度是对地的绝对加速度.除了列出动力学方程,还需列出动量守恒方程,并且能够判断物体做匀加速运动,利用运动学公式列出两个方程.

新解：以地面为参考系,设A向右运动的加速度大小为aA,B向下运动的加速度大小为aBy,B与C一起向左运动的加速度大小为aC,则A与B相对于C运动的加速度大小为

a=aBy

由于A与C运动方向相反,则相对加速度大小为

a=aA+aC

对A、B整体在细绳张力方向由牛顿第二定律有

mBg=mAaA+mBaBy

对A、B、C整体在水平方向由牛顿第二定律有

0=mAaA-(mB+mC)aC

联立上式可得

点评:首先要设置各质点加速度物理量的符号,明确各加速度之间的关系,即物体B运动的加速度在水平方向的分量与物体C的加速度相同,在竖直方向的分量与物体A相对于物体C运动的加速度大小相等.整个解题过程只需对加速度设置4个未知量,列出4个方程,其中两个方程用来反映某一方向的相对加速度与绝对加速度的关系;另外两个方程用来反映质点组在某一方向受到的合外力与加速度和质量的关系.

【例2】[2]如图2所示, 在一质量为M的小车上放一质量为m1的物块,它用细绳通过固定在小车上的滑轮与质量为m2的物块相连,物块m2靠在小车的前壁上而使悬线竖直.忽略所有摩擦,问:(1)当用水平力F推小车使之沿水平桌面加速前进时,小车的加速度多大?(2)如果要保持m2的高度不变,力F应该多大?

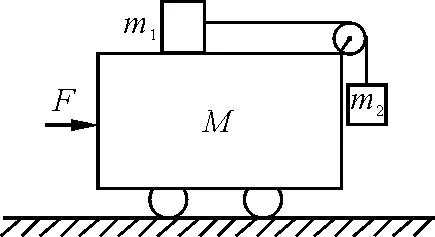
图2 例2题图

原解:(1)[2]分析小车和两个物块受力如图3所示.各力之间的关系为T1=T′1=T2=T′2,N=N′.以小车为参考系,物块m1和m2的相对加速度分别为a1和a2,则二者大小相等,即a1=a2.

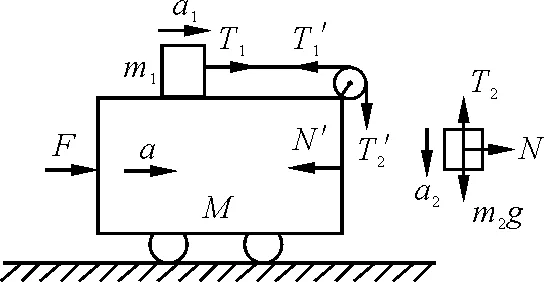
图3 分析各质点受力

设小车的加速度大小为a,方向向右,若以小车为参考系,则m1受到向左的惯性力大小为m1a,对m1沿水平方向由牛顿第二定律有

T1-m1a=m1a1

对m2沿竖直方向有

m2g-T2=m2a2

联立各式得

对m2沿水平方向有

N=m2a

对小车沿水平方向有

F-N′-T′1=Ma

联立这3个方程,考虑到T1=T′1,N=N′,可得

(2)[3]如果m2的高度保持不变,则相对加速度a1=0,由

可得

代入小车的加速度关系式可得推力大小为

点评:对于第(1)问,在非惯性系中应用牛顿第二定律列方程时,需对m1考虑惯性力.对于第(2)问,是利用第(1)问所得加速度代入特殊条件来求作用力,需对作用力的表达式式进行化简,难度较大.

新解:(1)以地面为参考系,设小车的加速度大小为a,物块m1的加速度大小为a1,物块m2向下运动的加速度分量a2y.若物块m1相对于小车向右运动,则m1相对于小车运动的加速度大小为a′=a1-a.物块m2向下运动的加速度分量与物块m1相对于小车运动的加速度大小相等,即a2y=a′.对m1、m2整体在沿绳移动方向由牛顿第二定律有

m2g=m1a1+m2a2y

对三者整体在水平方向由系统牛顿第二定律有

F=m1a1+(M+m2)a

联立方程可得

(2)若物块m2的高度保持不变,则三者的相对位置保持不变,加速度相同,对整体在水平方向由牛顿第二定律有

F=(M+m2+m1)a

对m1和m2整体在沿绳方向由系统牛顿第二定律有

m2g=m1a

联立方程可得

点评:对第(1)问,需首先对加速度设置未知量符号,并且设定物块m1相对于小车的运动方向,以便确定相对加速度与各加速度之间的数量关系.此外,物块m2的加速度在水平方向的分量与小车的加速度相同,在竖直方向的绝对加速度等于相对加速度.在应用系统牛顿第二定律列方程时,需选择不同的整体作为研究对象,并且选择正方向,分析整体受力情况以及各物体的加速度大小和方向.

还需讨论小车向左或向右运动的受力条件以及两个物体相对于小车向左或向右运动的条件[2].若推力F维持小车刚好静止不动,则m1和m2一起加速运动,因此二者的加速度大小相等,即为

由于例1是例2的特例,那么在解题时应用的规律和方法具有某些相似之处,利用例2第(1)问的结果,令F=0,可得小车的加速度为负值,其绝对值跟例1的结果相一致.

3 结束语

综上可见,由于模型中相互作用的物体个数较多,相对运动过程比较复杂,如果利用隔离法进行解答,过程繁琐,难度较大,而且易于出错.在地面参考系中利用整体法对质点组列出动力学方程的解法最简单.关键是在地面参考系中对3个物体分别设置加速度物理量符号,并且能够确切分析相对加速度与3个加速度之间的数量关系.在利用整体法对质点组列动力学方程时,要明确选择研究对象与正方向,其中在水平方向以3个物体为研究对象;在沿绳移动方向以两个物体为研究对象.利用整体法对质点组列动力学方程,不必分析系统内相互作用的力,可减少未知量与方程的个数,由此可化繁为简,显得巧妙快捷.此外,应用系统牛顿第二定律列方程要比应用质心运动定理列方程简便,有助于拓展解题思路和方法,提高解题的效率和效果.