RSA-BP组合模型在GNSS高程拟合中的应用
2023-10-10刘银涛王俊男何广焕
刘银涛,任 超,王俊男,张 炎,何广焕
(1.桂林理工大学测绘地理信息学院,广西 桂林 541004; 2.广西空间信息与测绘重点实验室,广西 桂林 541004; 3.广西壮族自治区自然资源遥感院,广西 南宁 530023; 4.广西建设职业技术学院市政与交通学院,广西 南宁 530007)
GNSS技术以全天候、高精度、经济便利、能够实时提供三维坐标等优点被广泛应用于测量工作中[1]。在实际工程应用中,我国国家高程系统采用正常高系统,而GNSS技术提供的是大地高系统。如何快速高效地获取两者的高程差,即高程异常值,从而提升大地高向正常高转换的精度,一直是测绘领域探索和研究的重点[2]。
GNSS高程拟合的方法较多,国外学者常用重力模型法解决该问题,但受限于国内高精度重力场模型未完善,无法在工程应用中使用。国内学者通常采用数学模型拟合法[3-5]和神经网络拟合法[6-7]求取高程异常值,如三次样条拟合法、多项式曲线拟合法、多面函数拟合法、最小二乘支持向量机(least squares support vector machine,LSSVM)等[8-11]。面对复杂地形区域时,常规拟合方法参数多、收敛速度慢,精度难以满足实际工作需求。
BP神经网络具有多元回归和多维函数映射能力,可以最大限度降低模型误差,但其参数存在随机性,易陷入局部最优。本文提出利用爬行动物搜索算法(reptile search algorithm,RSA)对BP神经网络各层之间的神经元权值和阈值寻优,利用RSA全局搜索能力强、参数少、收敛速度快的特点[12],为BP神经网络寻求最佳参数,进一步提高区域高程异常模型的预测精度。
1 爬行动物搜索算法原理
RSA是一种基于自然启发的元启发式优化算法。其灵感来自自然界中鳄鱼的包围机制、捕猎机制和社会行为,即通过高位步走或腹部爬行,以狩猎协调和狩猎合作的方式对猎物进行围捕,利用4种新颖的机制更新目标的位置,可以为复杂的问题提供更高质量的解决方案,得到新的最佳结果,帮助解决复杂的现实问题。与其他算法相比,RSA在优化问题中表现出明显的优越性[13]。具体实现原理如下。
1.1 初始化阶段
鳄鱼在捕食目标前,需要预估目标所在的位置,而鳄鱼个体所在位置视为最优候选解;当目标锁定后,鳄鱼群会根据目标位置和个体位置之间的关系进行信息的传递,其他个体也会向目标移动,不断更新自己的位置。优化过程从一组候选解开始进行,在每次迭代中获得的最优解视为最佳值,公式为
(1)
式中,X为随机生成的一组候选解;i为候选解;j为维度;xi,j为第i个候选解第j维的位置;N为鳄鱼候选解的数量;n为目标的维度大小。X的解算公式为
xi,j=rand×(UB-LB)+LB
(2)
式中,j的取值范围为[1,n];rand为[0,1]之间的随机数;LB和UB分别表示目标问题的上下界。
1.2 包围阶段(搜索行为)
RSA的搜索行为,即鳄鱼在围捕过程中的两种策略为:高位步走和腹部爬行。该策略要求鳄鱼不能接近目标猎物,防止目标受到干扰,旨在探索性地发现更广阔的搜索空间,找到最为密集的区域,实现包围阶段向狩猎阶段机制之间的转换。
在总迭代次数为T的前提下,高位步走策略取决于t≤T/4,腹部行走策略取决于t≤2T/4和t>4/T,包围阶段的位置更新公式为
x(i,j)(t+1)=Bestj(t)-η(i,j)(t)×β-
R(i,j)(t)×rand
(3)
x(i,j)(t+1)=Bestj(t)×x(r1,j)×ES(t)×rand
(4)
式中,xi,j(t+1)表示迭代至t+1时第i条鳄鱼所在j的位置;Bestj(t)表示截至迭代至第t次时最优值的第j维位置;η(i,j)表示第i个候选解的第j维的狩猎算子(见式(5));β为0.1,即一个固定的敏感参数,控制迭代过程中包围阶段的探索精度;R(i,j)为缩减函数(见式(6)),用于减少搜索区域的值;r1为[1,N]之间均匀分布的随机整数,N表示候选解的数量;x(r1,j)为随机位置r1的解;进化因子ES(t)表示在整个迭代次数中随机递减[-2,2]的一个概率比(见式(7))。
η(i,j)=Bestj(t)·P(i,j)
(5)
(6)
(7)
式(5)—(7)中,P(i,j)为获得最佳解决方案的位置和当前解位置之间的差异(见式(8));ε为一个很小的正数;r2为[1,N]之间的一个随机整数;r3为[-1,1]之间的一个随机值。
(8)
(9)
式中,M(xi)为第i个候选解的平均位置;UB(j)和LB(j)分别为第j维位置的上下界;α为用于控制迭代过程中狩猎合作的搜索精度的一个敏感参数,其为固定值0.1。
1.3 狩猎阶段(开发行为)
鳄鱼在狩猎过程中采用狩猎协调与狩猎合作两种策略。与包围机制不同,该策略设计不同的强化技术,目的为让鳄鱼更加快速轻易地接近目标猎物。在狩猎阶段,利用机制在最优解附近强化搜索,增强沟通,实现近乎最优的解决方案。在该阶段搜索过程中,狩猎协调机制取决于t≤3T/4和t>2T/4,狩猎合作机制取决于t≤T和t>3T/4。狩猎阶段的位置更新方程
x(i,j)(t+1)=Bestj(t)·P(i,j)(t)·rand
(10)
x(i,j)(t+1)=Bestj(t)-η(i,j)(t)·ε-
R(i,j)(t)·rand
(11)
综上所述,RSA算法从一组随机的候选解开始,重复上述公式的迭代,根据两种行为、4种策略实现最优方案的选取。
2 BP神经网络
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。在结构上,BP神经网络具有输入层、隐藏层、输出层;在本质上,BP神经网络以网络误差平方为目标函数,采用梯度下降法计算目标函数的最小值[14]。BP神经网络所具有的多元回归预测能力、任意复杂的模式分类能力和优良的多维函数映射能力,解决了单一感知器无法解决的问题,且因其效率高、效果好,成为应用最为广泛的神经网络模型之一[15]。神经网络拓扑结构如图1所示。其中,x、y、z分别为输入变量、隐藏层和输出变量;n、m分别为输入层和隐藏层神经元数;l为输出目标值的维度。
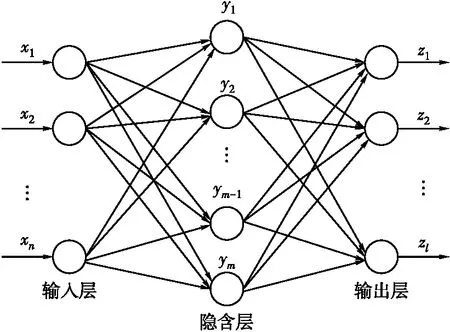
图1 神经网络拓扑结构
根据模型表达,BP神经网络不同神经元相互连接,自适应学习。正向传播时,各层神经元通过sigmod激活函数传递,当神经网络输出的真实值与预测值偏差较大时,模型得不到收敛,则需要执行反向误差传播。反向误差传播是以梯度下降的方式逆传递,对各层连接权值和阈值更新修改,降低输出值和预测值的均方误差。经过反复传播,权值阈值不断更新,当精度满足要求或迭代达到一定次数时,网络训练停止。
3 RSA优化BP神经网络权值阈值
BP神经网络在解决复杂模型问题时,误差曲面表现为一个凹凸不平的多维空间曲面[16],在迭代运算的过程中,易陷入局部极值,致使算法的收敛不为全局最优值,网络预测的结果较差。
因此,采用RSA所具有的全局搜索性特点,弥补BP神经网络的不足。网络中每条鳄鱼都是相互独立的个体,通过狩猎协调与狩猎合作的形式自发觅食,保持算法在全局搜索中的多样性。同时,以误差为适应度函数,不断更新鳄鱼的位置,实现优化BP神经网络的权值和阈值的作用。将优化后的参数代入神经网络模型中训练,从而提高算法的预测精度和收敛速度。RSA-BP神经网络的训练过程如图2所示。

图2 RSA-BP神经网络算法流程
(1)对采集的高程异常数据进行初步处理,剔除存在的粗差,保证试验数据的有效性和可靠性。确定BP神经网络输入层、隐藏层、输出层的节点数。
(2)对数据集进行归一化处理,得到初始化后神经网络的连接权值和阈值。
(3)利用训练集的均方误差作为RSA优化神经网络权值阈值的适应度函数。
(4)初始化RSA参数,设置鳄鱼种群规模、迭代次数及初始位置。
(5)由式(2)构建鳄鱼捕猎机制,利用构建的适应度值函数,确定当前最优鳄鱼个体所在位置。
(6)利用式(3)、式(4)中高位步走或腹部爬行策略执行包围机制,不断更新鳄鱼个体位置。
(7)利用式(10)、式(11)中狩猎协调或狩猎合作策略执行狩猎机制,再次更新鳄鱼个体位置;同时利用更新后鳄鱼个体位置计算适应度值,通过种群的不断迭代,最终保存鳄鱼最优个体位置,完成全局搜索。
(8)迭代结束后输出最佳的参数值,代入BP神经网络预测模型中进行训练;根据预测结果的残差、外符合精度对高程拟合模型进行精度评定。
4 试验分析
4.1 数据源
为验证RSA-BP神经网络在高程拟合模型中的适用性,选取两处不同地貌特征的测区进行测试研究。测区1为杭州湾跨海大桥,该测区大部分为海域,两岸地势平坦,高程异常不会发生剧烈变化;测区2为我国地形较为复杂的西南喀斯特地貌地区,地势起伏大,高程异常较为明显。对两测区以等精度的GNSS水准联测,设计3种不同方案进行对比,从而对3种模型进行精度评定。
4.2 沿海线形区域
杭州湾跨海大桥全长约36 km,宽度为33 m,桥段呈西北至东南方向布置,桥梁跨海区域加密网点呈线形分布[16]。均匀选取32个联测点作为工作集样本,用于构建拟合模型,12个联测点作为学习集样本。考虑数据的保密性,在不影响拟合效果的前提下,对坐标进行处理,联测点的地理分布如图3所示。对组合算法参数进行设置,将鳄鱼种群规模设置为50只,最大迭代次数为50,神经网络输入变量为2,隐含层为18,输出变量为1。图4为RSA算法收敛曲线。
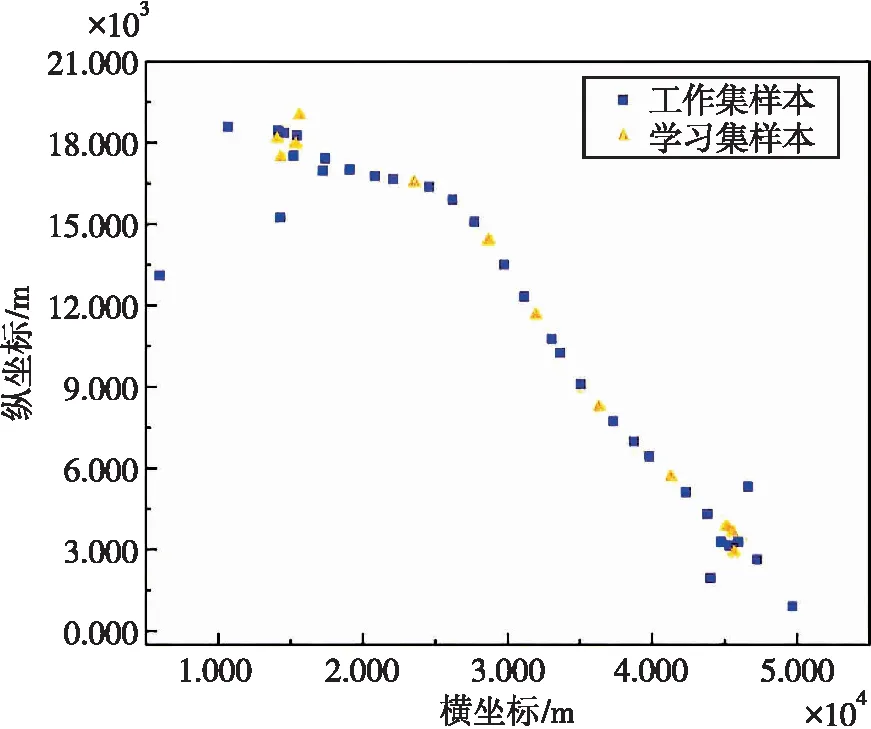
图3 线形区域点位分布

图4 RSA收敛曲线
为了验证RSA-BP神经网络算法在GNSS高程拟合中的实用性,使用相同数据组,将其与常用的多面函数法、常规LSSVM拟合法进行对比分析。为直观比较3种拟合方法在处理较为平坦的线形区域时的稳定性与有效性,统计了预测值与真实值的残差,对比如图5所示。

图5 不同模型检查点残差
由图5可以看出,RSA-BP神经网络拟合方法优于LSSVM拟合法和传统多面拟合法。3种算法残差绝对值均在4 cm内。LSSVM波动较大,稳定性差;多面函数拟合结果波动相对稳定,但个别点拟合结果较差;RSA-BP拟合方法则表现出更强的稳定性,拟合结果更趋近于真实值,精度明显提高。
为了避免偶然情况及精度分析的特殊性,利用3种拟合方法进行多次试验,选取10组数据的外符合精度,对比分析不同算法的拟合精度,见表1。

表1 精度拟合统计 cm
由3种算法10次精度的平均值可知,RSA-BP神经网络整体拟合精度更加稳定,可靠程度更高。同时,3种拟合方法单次拟合精度均在2 cm内,RSA-BP相较于LSSVM法,精度提高了36%;相较于多面函数法,精度提高了35%。可见,RSA-BP对小范围线形平坦区域高程拟合模型精度的提高具有明显的优势。
4.3 内陆面状区域
我国西南喀斯特地貌区地势复杂,地形起伏大,受重力场影响,该区域高程异常值较大。为验证RSA-BP神经网络在地形复杂区域的有效性,采用广西某地区56个GNSS水准联测点进行算例分析,均匀选取36个点作为工作集样本,20个点作为学习集样本。联测点位分布如图6所示。

图6 面状区域点位分布
面状区域RSA-BP神经网络模型各参数设置与线形区域一致。分别构建3种算法拟合模型,计算各算法预测值与真实值的残差。模型解算精度见表2,检查点残差如图7所示。

表2 面状区域精度评定

图7 不同模型检查点残差
由表2可知,RSA-BP、LSSVM、多面函数模型的最大残差分别为2.473、2.698、4.684 cm,外符合精度分别为1.247、1.457、2.002 cm。RSA-BP表现出更好的拟合效果和普适性,较另外两种模型,拟合精度分别提高14%、38%。
由图7可以看出,多面函数残差峰值波动最大,误差明显;LSSVM波动区间相对平缓,但零刻度附近分布残差点位较少;由于使用RSA优化BP神经网络权值和阈值,增强了BP神经网络的搜索能力,其零刻度附近点位分布较多,曲线趋于平稳,总体精度高于其余两种方法,处理复杂模型表现明显优势。
5 结 语
本文研究了基于爬行动物搜索算法的高程拟合方法,在地势起伏较小的线形区域,传统的数学模型拟合法和组合算法均能满足精度要求,而RSA-BP拟合模型具备更高的精度和稳定性;在地形复杂区域,利用RSA全局快速寻优的特性对BP神经网络的连接权值和神经元阈值优化,建立不同特征的拟合模型,相较于LSSVM和多面拟合方法,精度分别提高14%、38%。
RSA-BP拟合模型在不同地形中均表现出较好的稳定性和适用性,且计算过程简单,程序易于实现,可有效避免BP神经网络收敛速度慢、易陷入极值等问题。对实际测绘工作具有一定的参考价值。
