导航星间链路体制星地时间同步性能及其相关因素分析

陈晓锋,白 燕,郭燕铭,王 荣,彭思琦

(1.中国科学院国家授时中心,陕西 西安 710600; 2.中国科学院大学,北京 100049)

北斗三号卫星导航系统(BeiDou Navigation Satellite System,BDS-3)于2020年7月31日开通运行。由于BDS-2难以在全球实现测运控布站[1],北斗三号卫星通过星间链路(inter-satellite link,ISL)技术解决这一难题。每颗卫星都搭载了Ka频段星间链路设备,卫星与卫星之间可以进行星间测量和时间同步,进而实现导航星座自主导航,从而提升导航系统自主运行能力[2-5]。

利用北斗星座部署的优势,将导航体制星间链路技术应用于星地时间同步是一种较好的远程高精度时间传递方法。文献[2]提出了一种不依赖预报钟速信息的星地时间同步方法,直接利用原始伪距测量值进行星地时间同步。文献[6]在理论上推导了星间链路体制下星地双向时间同步的数学模型,对1 h、1 d的钟差数据进行拟合,拟合精度均优于0.3 ns。文献[7]介绍了Ka频段的双向测量模型,分析了影响时间同步精度的多个评价指标。文献[8]提出了一种基于最小二乘拟合的星地双向时间同步和测距算法,算法时间同步精度优于3 ns,测距精度优于3 m。文献[9]对北斗星间链路闭合残差进行了检测和分析,通过整网平差模型进行钟差修正,修正后星间钟差随机噪声减少了30%～50%。

由于星地时间同步通过双向单程测量能够抵消掉大部分信道误差,提高了测量精度,但仍会有因部分上下行路径不一致所引起的残留误差,影响最终时间同步性能。为了保证星地时间同步精度,一般需要利用轨道信息对上下行几何路径时延误差等进行修正。本文首先介绍星地双向时间同步的基本原理与方法;然后对时间同步过程中的主要误差进行分析,重点分析轨道精度对时间同步性能的影响;最后利用不同精度的轨道对星地实测数据进行分析与验证,以期为星地实现高精度时间同步提供一定的技术参考和积累。

1 星地双向时间同步原理

双向时间同步原理如图1所示,在卫星A和地面站B之间建立一条测距链路,假设卫星A钟面时与地面站B钟面时之间的钟差为Δt,建链双方在同一时刻互发测距信号,分别测得双向单程伪距值,联立可得如下伪距方程

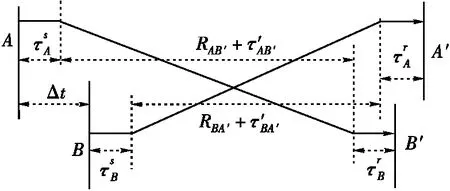
图1 星地双向时间同步原理

(1)

对伪距作差,可得星地钟差的求解公式为

(2)

其他附加链路时延τ′主要包括电离层时延、对流层时延、周期性相对论效应、相位中心偏移、引力时延等。其中,电离层时延受信号的频率与传播路径影响,在星间链路体制中,上下行信号频率相同且处于高频段,进行历元归算和伪距作差后上下行电离层时延几乎可以完全抵消[10];对流层时延可以通过Klobuchar模型进行修正[11],相位中心偏移可以通过将收发天线相位中心标定到同一基准点进行修正[12];周期性相对论效应、引力时延等在星间链路体制中对同步精度影响较小,在此不作讨论。

对于几何路径时延,假设建链双方相对静止且在同一时刻发送信号,则上下行几何路径时延完全对称,即RAB′-RBA′=0。由于北斗导航星间链路采用的是单频时分双工体制,该模式下卫星和地面站在不同时隙发送和接收信号,且卫星与地面存在一定的相对运动。因此,首先需要对建链双方接收到的伪距值进行历元归算,将上下行伪距接收时刻归算到同一时刻;然后进一步对上下行几何路径不一致误差以及其他各类误差进行补偿和修正;最后才能正确解算出星地相对钟差,从而实现星地时间同步。

2 几何路径时延误差修正

几何路径时延如图2所示,RA(t)为卫星在t时刻的三维坐标,RB(t)为地面站t时刻的三维坐标。假设卫星A的发射时刻与接收时刻分别为t0、t1,地面站B的发射时刻与接收时刻分别为t′0、t2。在t0时刻卫星向地面站发送测距信号,地面站在t2时刻接收。在t′0时刻地面站向卫星发送测距信号,卫星在t1时刻接收。

图2 几何路径时延示意

在星地时间同步过程中,由于卫星的高速运动,卫星接收时刻位置相较于发射时刻位置有明显变化,因此导致上行几何距离与下行几何距离不一致,该时延τ可表示为

(3)

式中,t0为卫星发射时刻;t2为地面站接收时刻;RA(t)为卫星在t时刻的三维坐标;RB(t)为地面站t时刻的三维坐标。在计算几何距离时,卫星与地面站应当在同一坐标系内,本文卫星与地面站坐标均在地心地固坐标系(earth-centered earth-fixed,ECEF)内。

通过历元归算将下行伪距ρAB(t2)归算到ρAB(t1)后,可知几何路径时延τ主要取决于卫星发射时刻t0、地面站接收时刻t1、卫星位置RA(t)及地面站位置RB(t)4个因素。在星地双向时间同步过程中,地面站接收时刻t1可由接收机直接测得;由于精确的卫星发射时刻ts未知,只能根据地面站接收时刻t1的伪距ρ(t1)进行反推,得到大致发射时刻,ts的计算公式为

(4)

式中,c为真空光速;t1为地面站接收时刻;ρ(t1)为地面站t1时刻接收到的伪距。

在地心地固坐标系中,卫星位置可以通过轨道信息得到,地面站位置可以提前标定,但此时需要额外考虑地球自转引起的Sagnac效应[13]。若地球自转角速度为ω,卫星A的ECEF坐标为(XA,YA,ZA),地面站B的ECEF坐标为(XB,YB,ZB),则Sagnac效应可表示为

(5)

3 轨道信息对几何路径时延误差的影响分析

卫星位置可以通过轨道信息得到,目前北斗公开的轨道信息有精密星历和广播星历。广播星历也称为预报星历,包括参考时刻、对应的开普勒轨道根数和轨道修正项。精密星历是一种经事后处理得到的卫星轨道信息,精度一般优于5 cm[14];其按一定的时间间隔(通常为5 min或15 min)给出一组卫星在地固坐标系下的位置、速度等信息。由于精密星历播报的卫星位置时间间隔较长,还需对精密星历进行插值处理。拉格朗日插值法可以对卫星精密星历进行准确内插[15],插值后可以得到需要的卫星发射时刻与卫星接收时刻的位置。

不同时刻的几何路径时延受轨道影响,对其进行试验分析。利用国家授时中心某Ka地面站与北斗M1卫星的一组星地实际测量伪距,采用广播星历计算几何路径时延及其变化率,结果如图3所示。

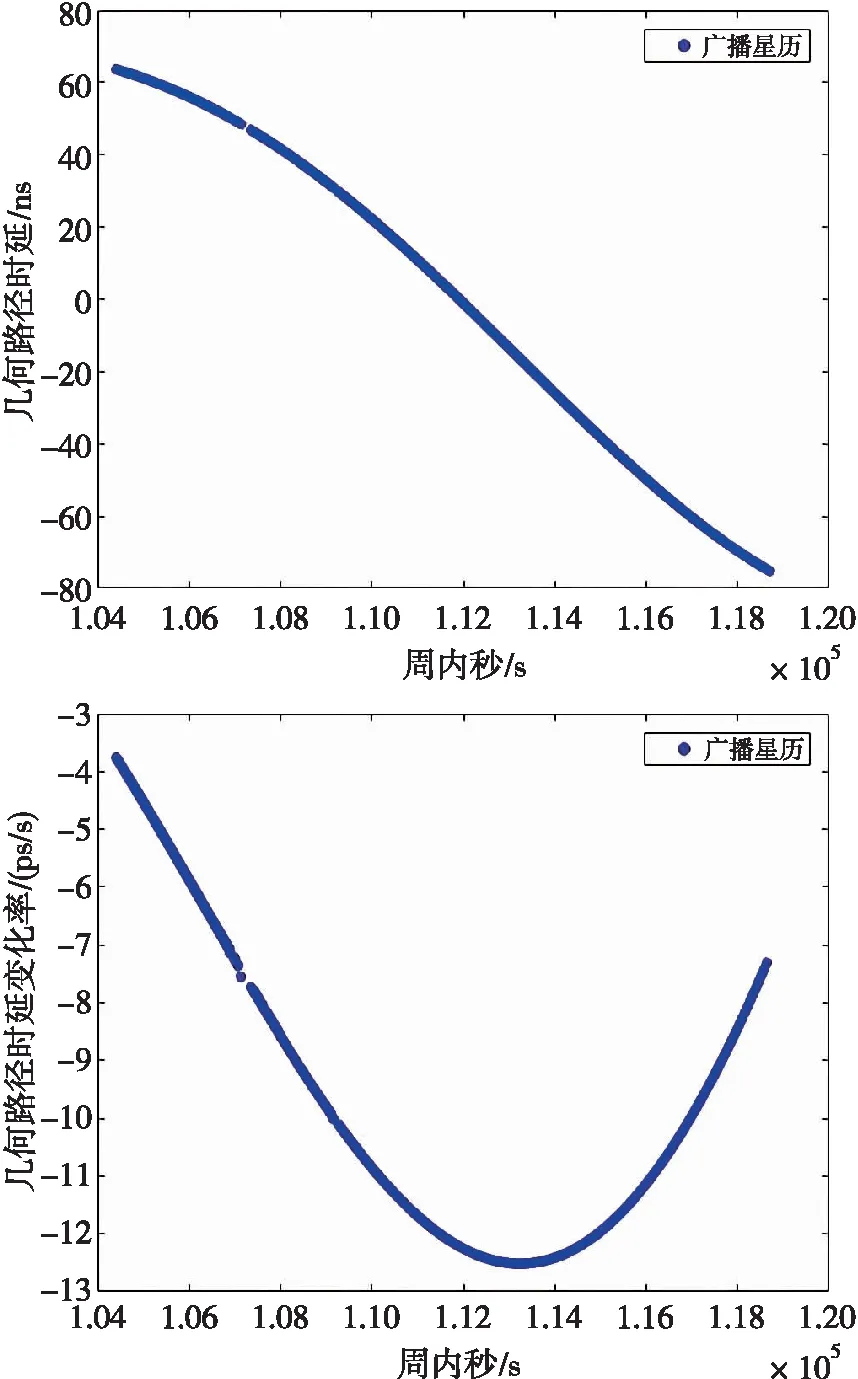
图3 几何路径时延及其变化率

由图3可以看出,采用广播星历计算得到的几何路径时延在几十纳秒量级,几何路径时延变化率在10 ps/s量级,对星地时间同步影响较大。

4 轨道精度对星地时间同步性能的影响分析

4.1 不同轨道精度的影响

卫星轨道会影响最终的时间同步精度。为研究不同轨道精度对星地时间同步性能的影响,选取2019年1月7日国家授时中心某Ka地面站与北斗M1卫星的实测数据,数据时长为1 h,使用精密星历进行钟差解算,对该钟差采用二阶多项式拟合。图4为使用精密星历解算得到的钟差拟合残差,使用精密星历得到的钟差拟合残差在0.1 ns量级,拟合残差RMS值为0.046 ns。

图4 精密星历解算钟差结果

同时使用广播星历进行钟差解算,求得广播星历解算得到的钟差拟合残差RMS。广播星历解算结果如图5所示。可以看出,使用广播星历时钟差拟合残差也在0.1 ns量级,拟合残差RMS值为0.058 ns。在星间链路体制下使用广播星历进行钟差解算,得到的钟差精度与使用精密星历得到的精度相差不大(见表1),广播星历的钟差拟合残差RMS值为0.058 ns,精密星历的钟差拟合残差RMS值为0.046 ns,广播星历与精密星历的RMS值均优于0.1 ns。

表1 不同轨道解算的钟差拟合残差RMS值ns

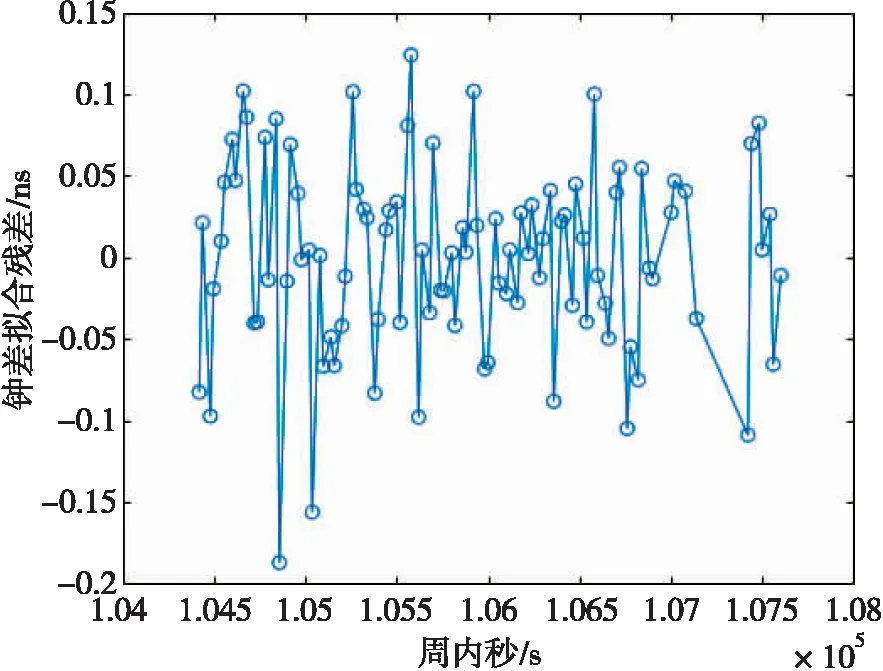
图5 广播星历解算钟差结果

进一步以广播星历得到的位置作为真实参考轨道位置,参考位置上对X、Y、Z方向附加随机噪声,研究不同轨道精度对星地时间同步性能的影响,用附加噪声后的位置进行钟差解算。广播星历附加噪声大小见表 2。

表2 广播星历附加噪声大小 m

在广播星历上附加3种不同大小的随机误差后,解算得到的钟差残差如图6所示。圆形为广播星历附加0.1 m误差,此时钟差残差RMS值为0.233 ns;正方形为广播星历附加1 m误差,此时钟差残差RMS值为2.238 ns;星形为广播星历附加5 m误差,此时钟差残差RMS值为11.677 ns;3种情况下最大残差值为35.35 ns。可以看出,广播星历叠加1 m以上的随机噪声后,对星地时间同步性能影响较大。

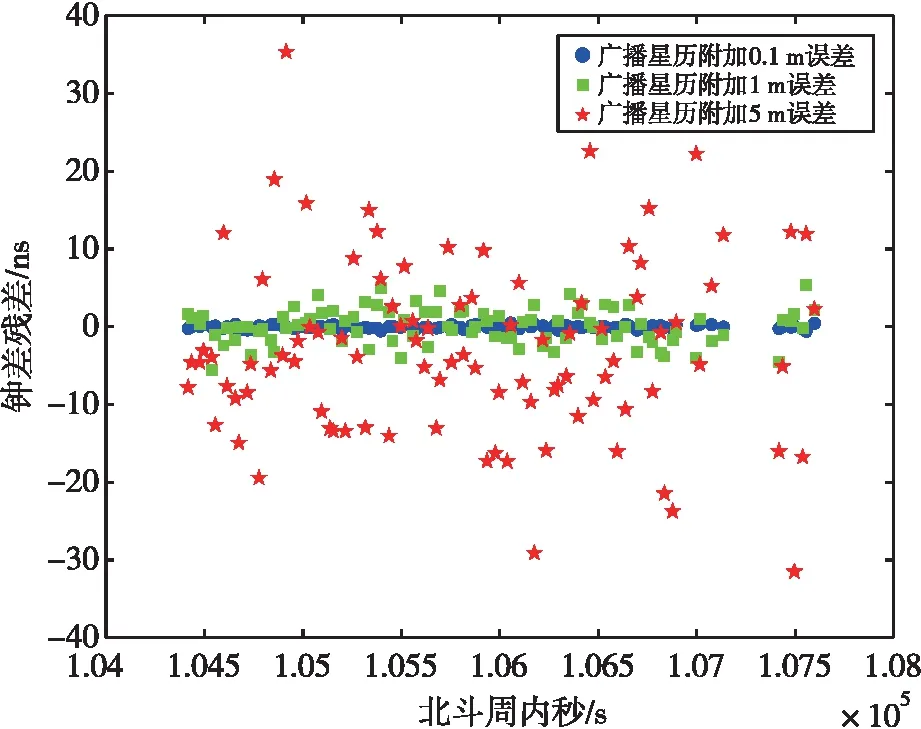
图6 广播星历附加噪声(滤波前)

4.2 通过滤波处理提高时间同步性能

通过上述分析可知,当广播星历中叠加一定的随机噪声后,星地时间同步精度受到较大影响。为了保证时间同步的精度,需要对叠加随机噪声后的轨道进行预处理,减小噪声对星地时间同步精度的影响。本文采取多项式拟合法对附加随机噪声的轨道进行平滑处理,滤掉随机误差部分,使轨道误差表现为慢变特性。对叠加不同误差的轨道进行平滑处理后的钟差拟合残差如图7所示。圆形为广播星历附加0.1 m误差,此时钟差残差RMS值为0.061 ns;正方形为广播星历附加1 m误差,此时钟差残差RMS值为0.069 ns;星形为广播星历附加5 m误差,此时钟差残差RMS值为0.082 ns;3种情况下最大残差为0.17 ns。

图7 广播星历附加噪声(滤波后)

表3为在广播星历的基础上附加不同噪声,平滑前后的钟差残差RMS值。可以看出,在广播星历上附加随机噪声对双向时间同步精度的影响较大,这是因为双向时间同步过程无法相互抵消随机误差;广播星历附加噪声后,通过多项式拟合的方法平滑轨道,可以有效降低随机误差对双向时间同步精度的影响,平滑后钟差残差RMS值均优于0.1 ns。

表3 平滑前后钟差RMS值ns

5 分析和结论

本文介绍了星地双向时间同步的基本原理与方法,对时间同步过程中的主要误差进行分析,给出了修正方法;并针对不同轨道精度对时间同步精度的影响,利用1 h实际测试数据进行了验证和分析。结果表明:①在星间链路体制下使用广播星历和精密星历解算钟差时,实现的星地时间同步精度均优于0.1 ns;②当广播星历叠加随机误差时,双向时间同步过程无法将该误差消除,随机误差对时间同步精度影响较大,通过平滑处理方法可以减小随机误差对时间同步精度的影响,平滑后钟差拟合残差RMS值优于0.1 ns。