基于熵权-TOPSIS法的渠系配水模型求解算法综合评价

卢德友，田桂林，杨泊，秦京涛

▪灌溉水源与输配水系统▪

基于熵权-TOPSIS法的渠系配水模型求解算法综合评价

卢德友1，田桂林2,3*，杨泊2，秦京涛2

（1.河南水利与环境职业学院，郑州 450011；2.中国农业科学院 农田灌溉研究所/农业农村部节水灌溉工程重点实验室，河南 新乡 453002；3.中国农业科学院 研究生院，北京 100081）

【目的】探究粒子群算法和天牛群算法在求解灌区渠系配水模型时的性能差异及优化后配水方案的共有特性。【方法】以大功灌区总干、分干两级渠系为研究对象，依据灌区不同的用水情形将其划分为18个配水对象，以灌溉用水总量、渠系渗漏水量及总干渠流量波动大小为优化目标，以下级渠道输水流量和输水启、闭时间点为决策变量，构建多目标两级渠系配水模型，分别使用粒子群算法和天牛群算法对模型进行求解，基于求解结果结合熵权-TOPSIS法对2种算法的性能进行综合评价。【结果】熵权-TOPSIS法的评价结果表明，粒子群算法的整体性能优于天牛群算法，但后者的计算速度高于前者。此外，同一用水情形下2种算法求解的配水方案相近，且优化后的下级渠道配水流量与配水时长存在共性规律。【结论】“左右须”寻优机制的引入使天牛群算法的计算速度相比粒子群算法最高可提升56%，但由于“左右须间距”初始参数的设置问题，随着计算维度的增加，粒子群算法的整体性能优于天牛群算法。研究结果可为灌区渠系配水管理提供科学依据。

灌区；渠系配水；天牛群算法；粒子群算法；熵权-TOPSIS评价模型

0 引言

【研究意义】科学的灌区水资源管理方案和渠系工作制度能够提高灌溉水利用效率，稳定粮食产能。灌区内同级渠道的控制灌溉面积和输水能力的差异会导致渠道间的灌水时长差异较大，设置不合理的渠道流量和配水时长是实际灌溉过程中产生灌溉水无效损失的主要原因之一。科学的渠系工作制度是保障灌溉水高效配置的基础[1]。

【研究进展】随着研究的深入和渠系配水模型复杂程度的增加，高效的求解算法是寻求合理配水方案的必要条件。部分学者在开展灌区渠系配水模型研究的同时也对相关算法的寻优能力进行了比较。一般从求解结果、求解速度及算法对不同问题的求解能力3个方面来评价多目标算法的整体性能[2]。褚宏业等[3]分别使用遗传算法和粒子群算法求解多目标渠系模型，得出粒子群算法的运算速度更快、配水结果更科学。李彤姝等[4]结合优化目标的计算结果和具体的配水方案，对比分析得出了粒子群算法相比向量评估遗传算法和回溯法具有更好的优化性能。韩宇等[5]通过比较回溯搜索算法、多目标粒子群算法及向量评估遗传算法，分别求解渠系配水模型时的计算速度和结果稳定性，指出回溯搜索算法的优势更为明显。Sun等[6]分别使用灰色关联分析法和TOPSIS法评价了遗传回溯搜索算法、向量评估遗传算法在求解渠系配水模型方面的性能表现，但评价指标仅基于计算结果，并未考虑求解速度和算法的自身特点。目前，越来越多的学者开始关注从不同角度出发，对多种算法进行全方位的对比分析[7-8]，从而发掘不同算法的优缺点。粒子群算法在灌区渠系配水研究中的应用趋于成熟，且整体表现良好。以天牛觅食为原型的天牛须搜索算法提出时间较晚，目前已应用于电力调度、路径规划及图形处理等方面[9]。天牛群算法是天牛须搜索算法的变体，其与粒子群算法均属于群体智能算法，对解决灌区复杂的渠系配水优化问题中具有一定潜力[10]。目前，对上述2种算法求解渠系配水模型时的性能表现仍缺乏详细的对比和综合评价。TOPSIS法常用于评价多处理、多指标问题。目前，基于熵权的TOPSIS评价法的评价结果准确、客观，因此常被应用于多处理试验结果评价[11-12]、产品优劣判别[13-14]、水资源承载力评价[15]及灌区节水能力评价与筛选[16-17]等领域。此外，TOPSIS法也被应用于筛选多目标配水模型的最优结果。赵钦等[18]使用NSGA-Ⅲ算法求解了区域水资源优化配置模型，并采用TOPSIS法对多目标帕累托可行解进行综合评价，筛选出了最佳的折中配置方案。【切入点】传统的渠系配水算法比较大多集中于直观且单一的计算结果对比，缺乏客观的综合性能评价。目前，基于熵权-TOPSIS法对渠系配水模型求解算法进行综合评价的研究仍较为缺乏。

【拟解决的关键问题】鉴于此，本研究以大功灌区总干-分干两级渠系为研究对象，依据灌区实际灌溉过程中的不同用水情形将其分为18个配水对象，分别使用天牛群算法和粒子群算法对配水方案进行求解，结合熵权-TOPSIS法对2种算法的计算速度与求解结果进行综合评价，研究结果可为灌区渠系配水研究的开展和算法优选提供参考。

1 材料与方法

1.1 多目标两级渠系优化配水模型

灌区渠系配水方案的优劣与各级渠道的流量、水流波动及配水时长相关。为寻求科学的配水计划，减少渠系渗漏水的无效损失、提高灌溉水输送效率、保证渠道水流的平稳运行，以灌溉用水总量、渠系渗漏水量、总干渠流量波动最小为优化目标，以下级渠道配水净流量和输水启、闭时间点为决策变量，建立多目标两级渠系优化配水模型。

1）优化目标一的表达式为：

式中：W为某次灌水周期内两级渠系输水所产生的渗漏总水量（m3）；为上级渠道流量产生变化时的某一阶段，∈，取值范围为1；及分别为全断面衬砌渠道渗水损失修正系数、土壤透水性系数、土壤透水性指数；为上级渠道的输水长度（km）；ΔT为第阶段上级渠道的输水时间（s）；Q为第阶段上级渠道的输水净流量（m3/s）；为下级渠道编号，∈，取值范围为1；l为第条下级渠道的长度（km）；tontoff分别为第条下级渠道开始和结束输水的时间点（s）；q为第条下级渠道的输水净流量（m3/s）。

2）优化目标二的表达式为：

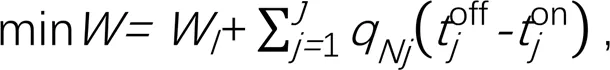
式中：为全灌区（含渠系渗漏水损失量）所需的灌溉总水量（m3）。本研究假设两级渠系在输送灌溉水的过程中不存在其他水量损失。

3）优化目标三的表达式为：

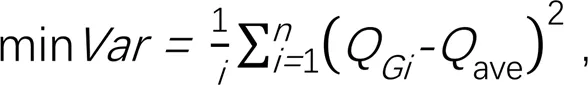
式中：为个阶段上级渠道流量随时间的波动变化；Q为第个阶段上级渠道的运行毛流量（m3/s）；ave为个阶段上级渠道毛流量的平均流量（m3/s）。

4）基础表达式为：

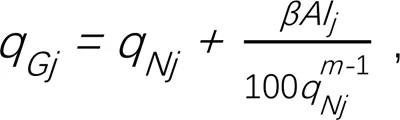
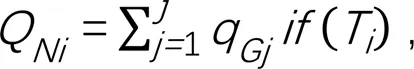
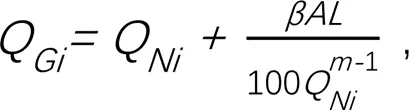
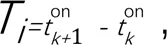
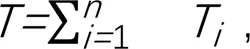
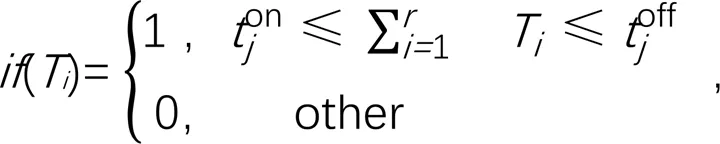
式中：q为第条下级渠道的输水毛流量（m3/s）；ton表示将第阶段所有灌水的下级渠道的闸门开启时间按照由小到大排序后得到的第个开启时间（s），∈，1≤；为整个灌溉周期（s）；为上级渠道流量变化的某个时段，∈，0≤≤。

5）流量约束条件为：

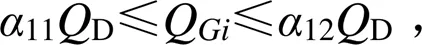
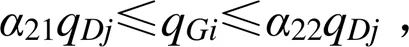
6）水量约束条件为：

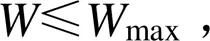
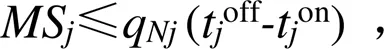
式中：max为渠首最大供水量（m3）；S为下级渠道的控制灌溉面积（m2）；为灌水定额（m3/hm2）。

7）时间约束条件为：

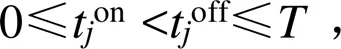
模型中计算渠系输水渗漏水量、流量以及所采用的渠道流量加大、最小系数参照《灌溉排水工程学》[19]。

1.2 粒子群算法（PSO）与天牛群算法（BSO）的主要差异

天牛群算法是以天牛须搜索算法[20]为基础，借鉴粒子群算法的寻优机制和整体框架所改进的一种群体智能算法[21]，解决了天牛须搜索算法在求解高维复杂问题时的局限性，补充了粒子群算法中单体粒子的寻优机制。2种算法在求解维模型时的群体位置更新式方面存在差异。与传统粒子群算法不同，天牛群优化算法在群体位置更新式中引入了单体天牛“左右须”搜寻机制，在天牛群体位置趋向全域极值移动的同时，通过表征个体与极值间的关系反映其对下次群体位置更新的影响，其余计算式与求解流程相同。

1.3 熵权-TOPSIS评价模型

TOPSIS评价法是一种逼近理想解的排序法，又称为优劣解距离法[22]。原理是通过计算不同处理下的各项指标值与理想解之间的距离，以此为基础进行打分、排序、综合评价。传统的TOPSIS法对不同指标进行主观权重赋值，评价结果的科学性不足，而熵权法通过计算各项指标自身的信息熵来设定权重，有效避免了上述问题。本研究使用熵权法确定不同指标间的信息熵和权重，并结合TOPSIS法评价不同算法的求解结果，筛选出整体性能最优的智能算法。

主要分析步骤如下：①分析整理待评价的样本数据，构建判断矩阵；②应用极差变化法对判断矩阵进行规范化处理；③求解指标变异度、信息熵，确定各项指标的权重；④构建加权后的决策矩阵，并计算正、负理想解；⑤基于欧氏距离计算各处理与正、负理想解之间的距离；⑥计算不同处理的得分并进行排序，筛选出最优结果。

1.4 研究区概况与参数设置

以河南省新乡市大功灌区为研究区域，以灌区内的总干渠、分干渠两级渠系为研究对象。灌区内年平均降水量为565.7 mm，降水年际变化较大，7—9月降水量占全年总降水量的60%，灌溉水源主要为黄河水，灌区年平均引水量为3 143.18万m3。大功灌区现状渠系水利用系数为0.560，灌溉水利用系数为0.495，农业用水效率偏低。以灌区渠系设计报告和2020年某次小麦的灌溉数据（灌水定额为1 200 m3/hm2）为基准，提取并简化全灌区总干渠、分干渠两级渠系，整理编号后的结果如表1所示。依据灌区实际的用水场景将其划分为18个配水对象，分别为：场景1（渠道12-14）、场景2（渠道1-4）、场景3（渠道5-8）、场景4（渠道5-9）、场景5（渠道10-14）、场景6（渠道9-14）、场景7（渠道5-11）、场景8（渠道12-21）、场景9（渠道1-8）、场景10（渠道1-9）、场景11（渠道5-14）、场景12（渠道12-21）、场景13（渠道1-11）、场景14（渠道10-21）、场景15（渠道9-21）、场景16（渠道1-14）、场景17（渠道5-21）、场景18（渠道1-21）。配水模型及求解算法的相关参数详见表2。

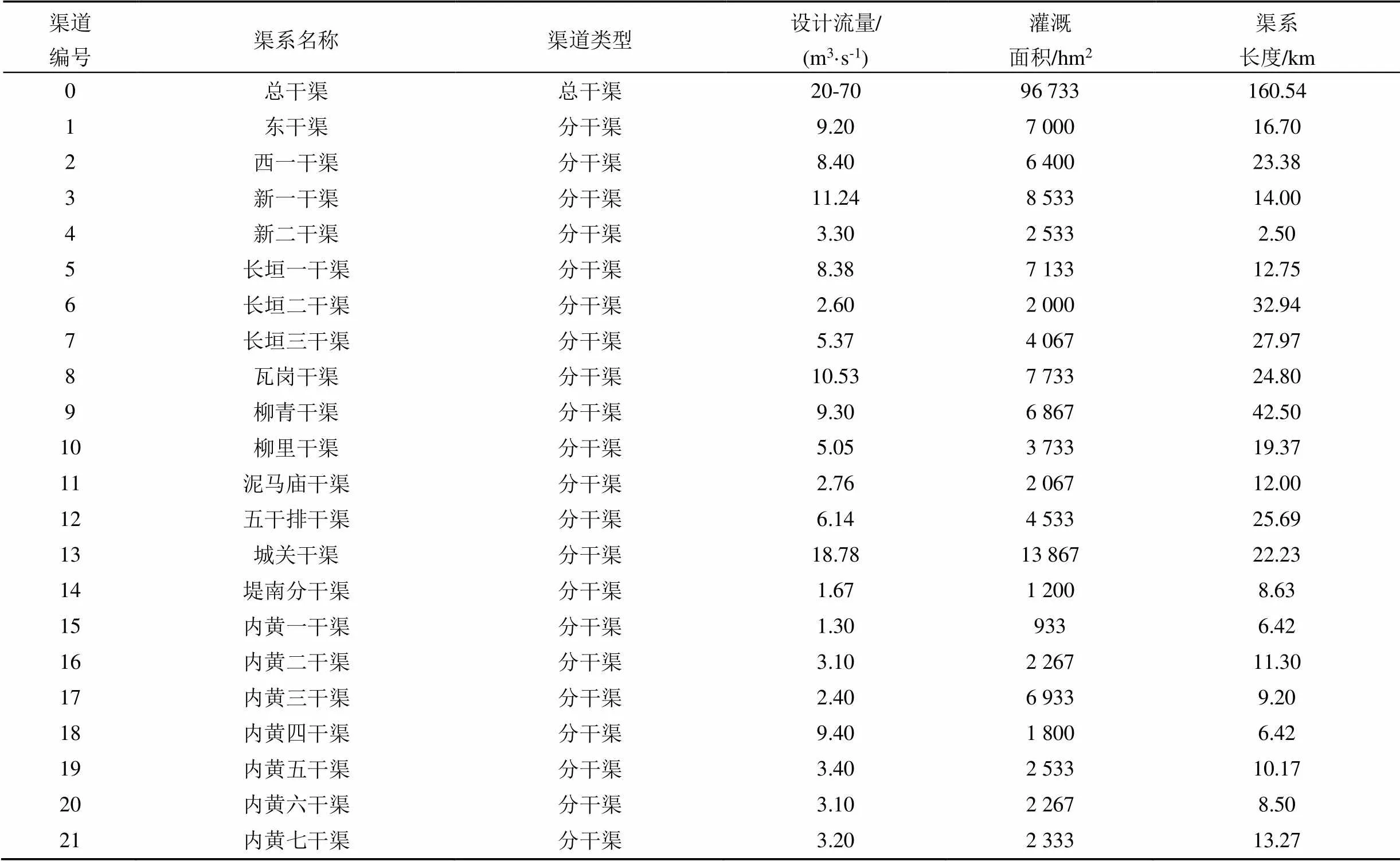
表1 渠系基础参数汇总

表2 配水模型与算法参数汇总

2 结果与分析

2.1 基于熵权-TOPSIS法的2种算法评价结果

基于天牛群算法和粒子群算法分别求解18种用水场景下的多目标两级渠系优化配水模型的计算结果如表3所示。为客观评价2种算法求解结果的优劣，以迭代次数、算法复杂度（算法计算流程的繁琐程度）、计算渗漏水量、计算总水量、计算干渠流量波动及计算配水时长6项参数为指标，以2种算法计算结果的平均值为基准数据，构建TOPSIS评价模型。其中，计算渗漏水量、总水量、干渠流量波动及配水时长可反映算法的寻优能力，计算结果越小表明算法的寻优能力越强。迭代次数和算法复杂度可体现算法的寻优效率，迭代次数越少、复杂度越低表明算法的寻优效率越高。

表3 2种算法求解配水模型的优化目标结果

2.2 不同用水场景下2种算法的寻优效率

图1为2种算法的迭代次数之差随模型计算维度增加的变化情况。在不同维度下，天牛群算法的迭代次数均少于粒子群算法，计算速度最高可提升56%，减少了近50%的运算时间，天牛群算法的寻优效率相比粒子群算法有明显提升。

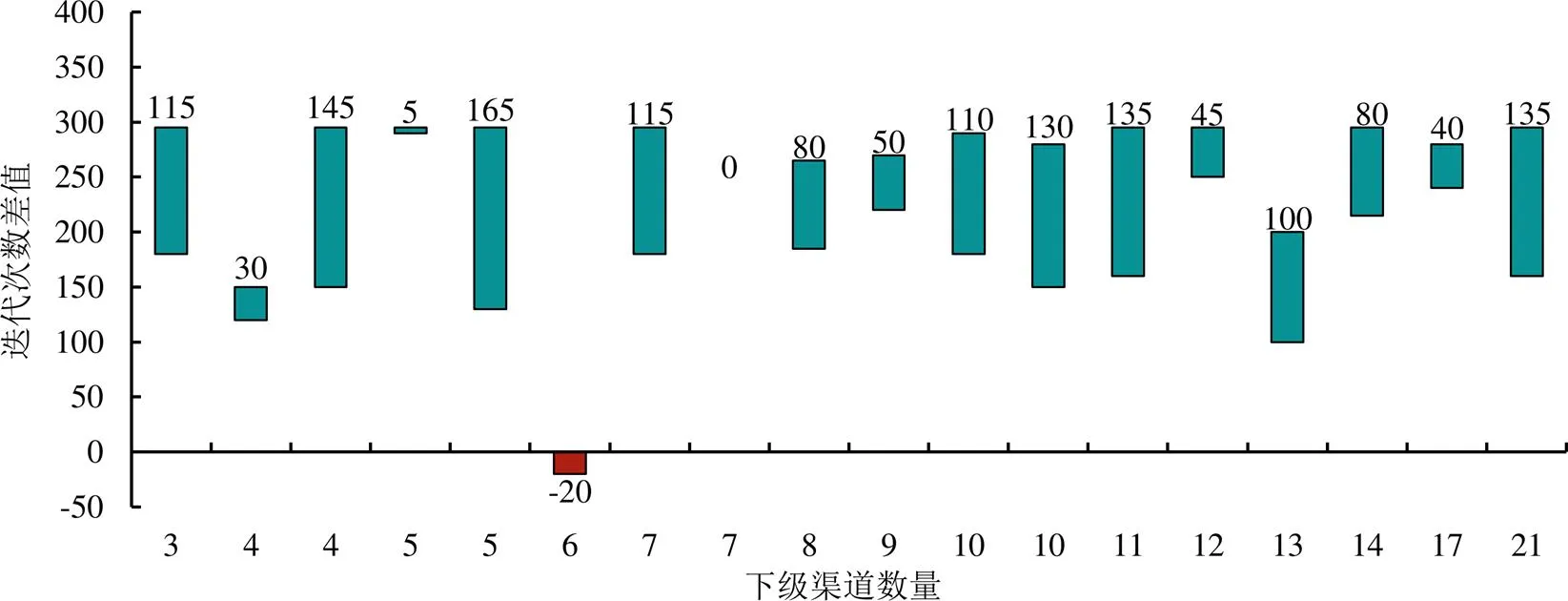
图1 2种算法在不同维度下的迭代次数差值

2.3 不同用水场景下2种算法的计算结果评价

使用熵权法计算指标权重，并结合TOPSIS法确定2种算法的得分与排序情况。通过评价不同用水场景下的计算结果，判别2种算法的性能表现。2种算法在18种配水场景下的评价得分差如图2所示。当下级渠道数量未超过5条时，天牛群算法的整体表现优于粒子群算法，但随着下级渠道数量的增加，后者的性能表现明显优于前者。

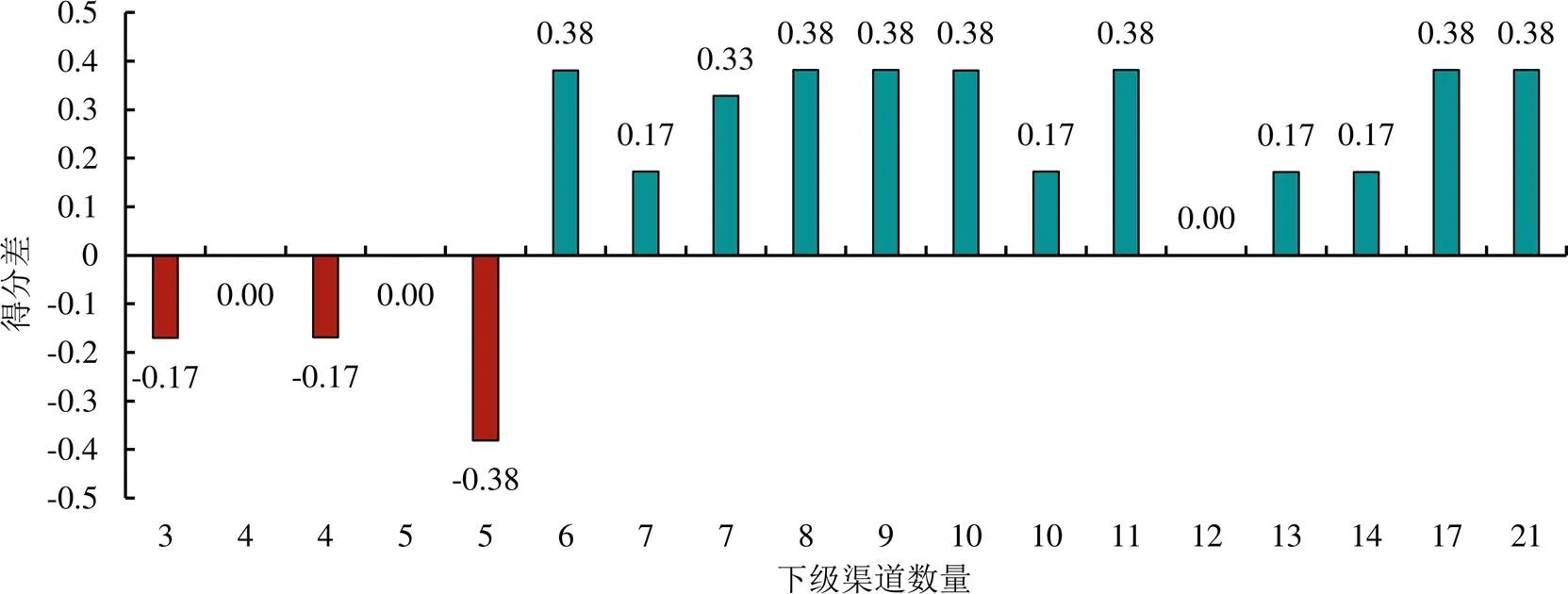
图2 2种算法在不同配水场景下的评价得分差

2.4 不同用水场景下2种算法的综合性能评价

由表4可知，粒子群算法的整体性能优于天牛群算法。结合2种算法的计算流程可知，天牛群算法在群体位置更新公式中引入了“左右须”寻优机制，这一机制使得整体的寻优效率相比粒子群算法有所提升，不同维度下配水模型的迭代次数均明显少于粒子群算法。然而，通过直观对比表3中3项模型优化目标的计算结果可知，粒子群算法的计算结果更为接近最优解，基于熵权-TOPSIS法的综合评价结果也证明了这一结论。原因可能是天牛群算法寻优机制中的“左右须间距”参数的初始值设定不合理，导致天牛群算法寻优时的步长过大，从而导致错过或忽略了较优解。在后续研究中，可通过调节初始参数的设定或引入衰减因子等措施解决这一问题。

2.5 多目标两级渠系配水模型求解结果分析

2.5.1 不同用水场景下的2种算法计算结果的差异

分别计算2种算法在不同用水场景下的渠道流量、配水时长以及启、闭配水时间点的求解值之差。由图3可知，2种算法的计算结果基本一致，下级渠道流量和配水时长差异较小。在部分场景下，由于求解模型时不同渠道间灌溉顺序的差异会导致在下级渠道配水流量与配水时长差值较小的同时，启、闭时间点的差异较大。随着下级渠道数量和计算维度的增加，2种算法的计算结果差异性也会随之增加。

表4 不同用水场景下2种算法的综合评价结果

此外，下级渠道设计流量会对2种算法求解结果的差异产生影响。以2种算法计算结果的差值超过了渠道设计流量和理论配水时长的10%为较大差异值渠道，其中小流量渠道（设计流量较小，渠道编号为4，6，11，14～17，19～21）占所有较大差异值渠道数量的63%，这是由于设计流量较小时所需要的计算精度更高，定义域内算法的检索步长更小，过大的步长设置会使得小流量渠道的计算值偏离最优解。

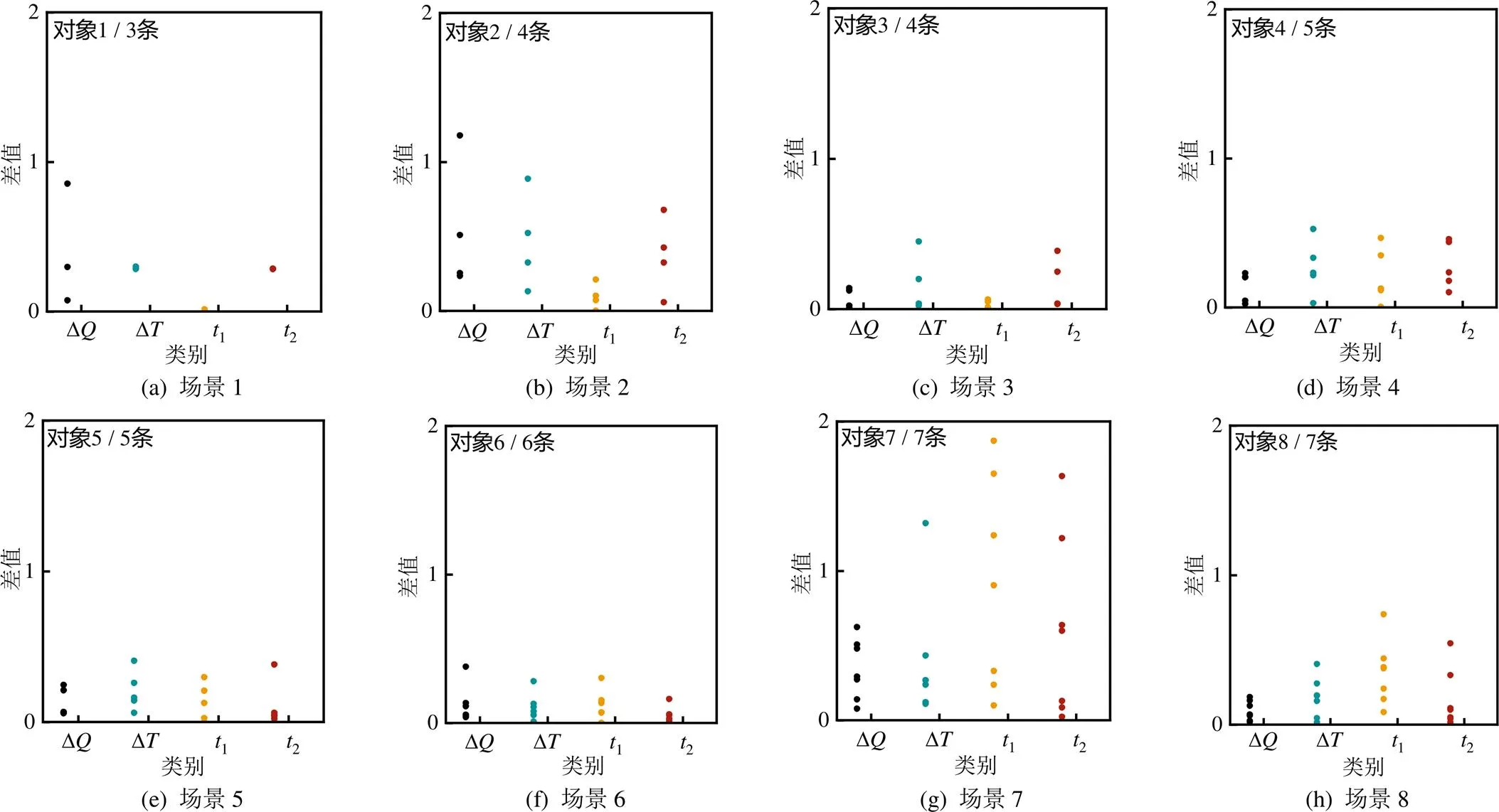
2.5.2 计算结果中配水流量和理论时间的共性规律

以下级渠道的设计流量和理论配水时间为参考，对2种算法、18个配水场景计算结果的共性特征进行分析，如图4所示。优化配水方案中的下级渠道流量不受求解算法类别、下级渠道数量的影响，优化后的下级渠道运行流量的范围稳定在各下级渠道设计流量与1.3倍的设计流量之间，概率峰度为1.2倍的下级渠道设计流量。同理，优化后的下级渠道配水时长范围介于各下级渠道理论配水时长与0.8倍的理论配水时长之间，概率峰度为0.8倍的理论配水时长。使用不同算法求解基于多个对象的多目标两级渠系配水模型的计算结果具有共性结论，即下级渠道流量与配水时长存在一个较优解范围。

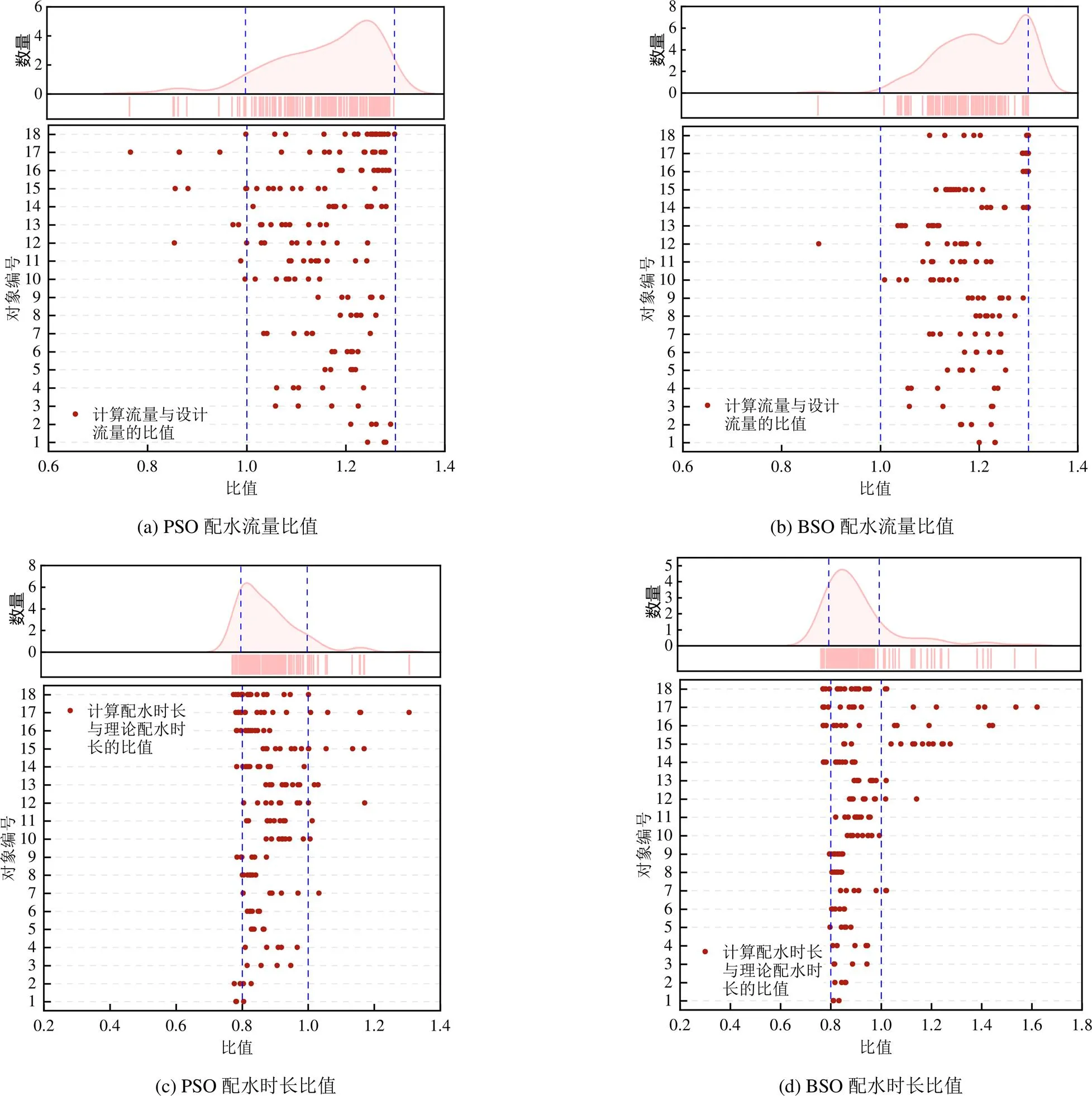
图4 不同用水场景下2种算法求解结果的共性特征

3 结论

1）“左右须”寻优机制的引入使天牛群算法的计算速度较粒子群算法最高可提升56%，但由于“左右须间距”等初始参数的设置问题，随着计算维度的增加，粒子群算法的整体性能优于天牛群算法。

2）求解出的不同用水场景下的配水方案存在共性规律，即优化后的下级渠道流量和配水时间的范围分别为：[设计流量，1.3倍的设计流量]、[0.8倍的理论配水时间，理论配水时间]。

（作者声明本文无实际或潜在的利益冲突）

[1] 李睿环, 郭萍, 张冬梅. 基于不确定性的渠系水资源优化配置[J]. 人民黄河, 2015, 37(11): 139-141, 148.

LI Ruihuan, GUO Ping, ZHANG Dongmei. Optimal water allocation of canal systems under uncertainty[J]. Yellow River, 2015, 37(11): 139-141, 148.

[2] 王丽萍, 任宇, 邱启仓, 等. 多目标进化算法性能评价指标研究综述[J].计算机学报, 2021, 44(8): 1 590-1 619.

WANG Liping, REN Yu, QIU Qicang, et al. Survey on performance indicators for multi-objective evolutionary algorithms[J]. Chinese Journal of Computers, 2021, 44(8): 1 590-1 619.

[3] 褚宏业, 王莹, 文俊, 等. 遗传算法和粒子群算法求解渠系多目标优化模型[J]. 中国农村水利水电, 2015(4): 9-11, 17.

CHU Hongye, WANG Ying, WEN Jun, et al. Genetic algorithm and PSO algorithm for solving canal system multiobjective optimization model canal[J]. China Rural Water and Hydropower, 2015(4): 9-11, 17.

[4] 李彤姝, 黄睿, 孙志鹏, 等. 基于多目标粒子群算法的渠系优化配水研究[J]. 灌溉排水学报, 2020, 39(9): 95-100, 125.

LI Tongshu, HUANG Rui, SUN Zhipeng, et al. Optimizing water distribution in canal networks using multi-objective particle swarm optimization method[J]. Journal of Irrigation and Drainage, 2020, 39(9): 95-100, 125.

[5] 韩宇, 孙志鹏, 黄睿, 等. 基于回溯搜索算法的灌区优化配水模型[J]. 工程科学与技术, 2020, 52(1): 29-37.

HAN Yu, SUN Zhipeng, HUANG Rui, et al. Optimized water distribution model of irrigation district based on the backtracking search algorithm[J]. Advanced Engineering Sciences, 2020, 52(1): 29-37.

[6] SUN Z P, CHEN J, HAN Y, et al. An Optimized water distribution model of irrigation district based on the genetic backtracking search algorithm[J]. IEEE Access, 2019, 7: 145 692-145 704.

[7] 刘恬恬, 李子明, 胡雅琪, 等. 灌溉渠系优化配水模型与算法研究进展[J]. 节水灌溉, 2022(11): 51-58.

LIU Tiantian, LI Ziming, HU Yaqi, et al. Review on optimal water allocation model and algorithm of irrigation canal system[J]. Water Saving Irrigation, 2022(11): 51-58.

[8] 韩宇, 邵梦璇, 李彤姝, 等. 河套灌区渠系优化配水模型应用研究[J].排灌机械工程学报, 2022, 40(10): 999-1 006.

HAN Yu, SHAO Mengxuan, LI Tongshu, et al. Study on optimal water distribution model of canal system in Hetao Irrigation District[J]. Journal of Drainage and Irrigation Machinery Engineering, 2022, 40(10): 999-1 006.

[9] 廖列法, 杨红. 天牛须搜索算法研究综述[J]. 计算机工程与应用, 2021, 57(12): 54-64.

LIAO Liefa, YANG Hong. Review of beetle antennae search[J]. Computer Engineering and Applications, 2021, 57(12): 54-64.

[10] 田桂林, 苏枫, 邹红, 等. 基于天牛群优化算法的灌区渠系配水研究[J]. 灌溉排水学报, 2022, 41(7): 96-103.

TIAN Guilin, SU Feng, ZOU Hong, et al. Calculating water distribution in irrigation channel networks using the beetle swarm optimization algorithm[J]. Journal of Irrigation and Drainage, 2022, 41(7): 96-103.

[11] 赵思腾, 师尚礼, 李小龙, 等. 基于熵权-TOPSIS模型筛选陇中旱作区适宜玉米轮作的土壤可持续系统[J]. 草地学报, 2019, 27(4): 997-1 005.

ZHAO Siteng, SHI Shangli, LI Xiaolong, et al. Application of TOPSIS based on entropy weight to screen soil sustainable systems suitable for corn rotation in the arid region of central Gansu[J]. Acta Agrestia Sinica, 2019, 27(4): 997-1 005.

[12] 虞娜, 吴昌娟, 张玉玲, 等. 基于熵权的TOPSIS模型在保护地番茄水肥评价中的应用[J]. 沈阳农业大学学报, 2012, 43(4): 456-460.

YU Na, WU Changjuan, ZHANG Yuling, et al. Application of TOPSIS model method based on entropy weight to evaluate coupling effect of irrigation and fertilization of greenhouse tomato[J]. Journal of Shenyang Agricultural University, 2012, 43(4): 456-460.

[13] 张芮, 李红霞, 高彦婷, 等. 基于熵权-TOPSIS模型的黄土高原半干旱区玉米覆膜类型综合评价[J]. 甘肃农业大学学报, 1-14[2023-08-10].

ZHANG Rui, LI Hongxia, GAO Yanting, et al. Comprehensive evaluation of film mulching types of maize in semi-arid area of loess plateau based on entropy weight - TOPSIS model[J]. Journal of Gansu Agricultural University, 1-14[2023-08-10].

[14] 岳焕芳, 郭芳, 王铁臣, 等. 基于熵权的TOPSIS模型在黄瓜适宜抗蒸腾产品评价中的应用[J]. 中国瓜菜, 2022, 35(2): 49-54.

YUE Huanfang, GUO Fang, WANG Tiechen, et al. Application of TOPSIS model based on entropy weight to evaluate coupling effect of suitable anti-transpiration products on cucumber[J]. China Cucurbits and Vegetables, 2022, 35(2): 49-54.

[15] 王艳, 雷淑珍. 黄河流域资源环境承载力评价研究[J]. 人民黄河, 2022, 44(8): 17-21, 33.

WANG Yan, LEI Shuzhen. Evaluation of resources and environment carrying capacity of the Yellow River Basin[J]. Yellow River, 2022, 44(8): 17-21, 33.

[16] 雪宝, 汤骅, 程泉, 等. 基于熵权TOPSIS法的灌溉用水效率评价[J]. 灌溉排水学报, 2023, 42(5): 82-89, 107.

XUE Bao, TANG Hua, CHENG Quan, et al. Evaluating irrigation water efficiency using entropy weight-TOPSIS method: A case study[J]. Journal of Irrigation and Drainage, 2023, 42(5): 82-89, 107.

[17] 张立志, 王昕, 谢文鹏, 等. 基于组合权重-TOPSIS法的灌区节水评价[J]. 灌溉排水学报, 2022, 41(S2): 65-70.

ZHANG Lizhi, WANG Xin, XIE Wenpeng, et al. Evaluation of water saving in irrigation district based on combination weight-TOPSIS method[J]. Journal of Irrigation and Drainage, 2022, 41(S2): 65-70.

[18] 赵钦, 白清俊, 聂坤堃, 等. 基于NSGA-Ⅲ算法与TOPSIS决策下的区域水资源多目标优化配置[J]. 排灌机械工程学报, 2022, 40(12): 1 233-1 240.

ZHAO Qin, BAI Qingjun, NIE Kunkun, et al. Multi-objective optimization allocation of regional water resources based on NSCA-Ⅲ algorithm and TOPSIS decision[J]. Journal of Drainage and Irrigation Machinery Engineering, 2022, 40(12): 1 233-1 240.

[19] 史海滨, 田军仓, 刘庆华, 等. 灌溉排水工程学[M]. 北京: 中国水利水电出版社, 2006.

[20] JIANG X Y, LI S. BAS: Beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1-5.

[21] WANG T T, YANG L, LIU Q A. Beetle swarm optimization algorithm: Theory and application[J]. Filomat, 2020, 34(15): 5 121-5 137.

[22] SHIH H S, SHYUR H J, LEE E. An extension of TOPSIS for group decision making[J]. Mathematical and Computer Modeling, 2007, 45(7/8): 801-813.

Comprehensive Evaluation of Two Canal Systems Water Distribution Model Solution Algorithms Based on Entropy Weight-TOPSIS Approach

LU Deyou1, TIAN Guilin2,3*, YANG Bo2, QIN Jingtao2

(1. Henan Vocational College of Water Conservancy and Environment, Zhengzhou 450011, China; 2. Farmland Irrigation Research Institute, Chinese Academy of Agricultural Sciences/Key Laboratory of Water saving Irrigation Engineering, Ministry of Agriculture and Rural Affairs, Xinxiang 453002, China;3. Graduate School of Chinese Academy of Agricultural Sciences, Beijing 100081, China)

【Objective】To investigate the performance difference between the Particle Swarm algorithm and the Beetle Swarm Optimization algorithm in solving the water distribution model of a two-level canal system in irrigation districts, as well as the common characteristics of the optimized water distribution schemes.【Method】This study takes the two-level canal system of Dagong Irrigation District as the research object, and divides it into eighteen water distribution scenarios according to different water use situations in the irrigation district. The total amount of irrigation water, the amount of water leakage and the fluctuation of the flow rate of the main canal are used as the optimization objectives. The decision-making variables are the flow rate of the sub-main canals and the opening and closing time points of the water transmission. Construct a multi-objective two-level canal distribution model, solve it using the Particle Swarm Optimization algorithm and the Beetle Swarm Optimization algorithm respectively, and comprehensively evaluate the performance of the two algorithms based on the solution results combined with entropy weight-TOPSIS method.【Result】The evaluation results of entropy weight-TOPSIS method show that the performance of the Particle Swarm Optimization algorithm is better than the Beetle Swarm Optimization algorithm, but the computational speed of the latter is significantly faster than that of the former. In addition, the water distribution schemes solved by the two algorithms under the same water use situation are close to each other, and there is a common law between the optimized water distribution flow and duration of the sub-main canal.【Conclusion】The results of the study can provide suggestions for the management of water distribution in two canal systems in irrigation districts and provide a basis for selection algorithms.

irrigation district; canal system water distribution; the particle swarm optimization algorithm; the beetle swarm optimization algorithm; entropy weight-TOPSIS evaluation model

1672 - 3317（2023）09 - 0129 - 09

S274.3

A

10.13522/j.cnki.ggps.2023367

卢德友, 田桂林, 杨泊, 等. 基于熵权-TOPSIS法的渠系配水模型求解算法综合评价[J]. 灌溉排水学报, 2023, 42(9): 129-137.

LU Deyou, TIAN Guilin, YANG Bo, et al. Comprehensive Evaluation of Two Canal Systems Water Distribution Model Solution Algorithms Based on Entropy Weight-TOPSIS Approach[J]. Journal of Irrigation and Drainage, 2023, 42(9): 129-137.

2023-08-14

2023-09-04

2023-09-15

2023年度河南省高等学校重点科研项目（23B570003）；中国农业科学院科技创新工程项目（ASTIP）

卢德友（1967-），男。副教授，硕士，研究方向为水利工程BIM与节水灌溉工程技术。E-mail: ldyueou@126.com

田桂林（1997-），男。博士研究生，研究方向为灌区渠系优化配水理论与应用。E-mail: ykerlove@163.com

@《灌溉排水学报》编辑部，开放获取CC BY-NC-ND协议

责任编辑：韩 洋