基于人工神经网络模型的混流式水轮机转轮多目标优化
2023-10-10王荣涛赖喜德陈小明
王荣涛,赖喜德,陈小明
▪灌溉技术与装备▪
基于人工神经网络模型的混流式水轮机转轮多目标优化
王荣涛,赖喜德*,陈小明
(西华大学 能源与动力工程学院,成都 610039)
【目的】探究一种同时提升混流式水轮机运行效率、空化性能及运行稳定性的优化方法,为混流式水轮机转轮的多目标优化提供技术途径。【方法】以转轮叶片进出口安放角、安装角为优化变量,通过对叶片几何参数随机离散抽样获取样本数据库,基于CFD数值计算获取各样本的性能参数,进而建立同时考虑混流式水轮机转轮效率、出口旋流数以及空化系数的多目标函数;基于人工神经网络建立优化变量与多目标函数的映射关系,最后采用遗传算法对转轮叶片的18个几何参数进行全局寻优,并对优化前后的转轮叶片性能进行对比分析。【结果】在导叶开度为112°且运行水头分别为160、175、180 m的3个工况下,优化后的转轮效率相较优化前分别提高了0.22%、0.56%、0.60%;叶片压力分布情况得到有效改善;转轮无叶区与尾水管锥管段处压力脉动幅值显著降低。【结论】叶片进口安放角的优化程度越大,混流式水轮机综合性能的提升幅度越大。
混流式水轮机;转轮;多目标优化;人工神经网络;遗传算法
0 引言
转轮是将水能实现能量转换的核心部件,随着我国对水力资源开发能力要求的逐步提高,提升水轮机的效率、空化性能以及变工况运行时的机组稳定性已成为转轮多目标优化设计所追求的目标[1]。【研究意义】现有的全三维反问题设计的转轮难以兼顾多工况的性能要求[2],因此需要研究高效、可靠的转轮多目标优化设计方法,该类方法可以最大限度减少水力设计过程中的人为因素、减少试验及降低设计生产中的成本,对于缩短叶片优化周期、提高转轮整体性能具有一定参考意义。
在转轮的多目标优化过程中,优化变量之间的参数相互耦合,目标函数易出现冲突,因此优化变量与目标函数之间良好的近似模型尤为重要[3]。随着人工智能的兴起、人工神经网络模型不断更新升级并朝着应用领域多元化的方向发展,该模型因具有较好的非线性映射、自适应能力而被逐渐应用于流体机械的多目标优化工作[4-6]。【研究进展】许多学者在该方面进行了深入研究。朱国俊等[7]基于径向基神经网络模型对潮流能水轮机叶片翼型进行了优化,以径向基神经网络替代优化过程中的CFD分析,提高了运行效率;赵斌娟等[8]采用BP人工神经网络模型对双流道泵蜗壳进行多学科多目标优化设计,较大程度上改善了蜗壳隔舌处及扩散段的回流现象,并且效率有所提升。该模型传统的基于梯度下降原则的优化方法具有良好的收敛性,但其收敛速度慢,精度低。随着仿生型智能优化算法的发展,人工神经网络模型与智能优化算法结合的方法逐渐取代以往的多目标优化方法[9],叶道星等[10]采用遗传算法对旋流泵转子叶片进行了全局优化,优化了叶片前缘的剪切应力,提升了运行效率;王掩刚等[11]基于神经网络和遗传算法,结合数值模拟手段对串列叶型进行了优化设计,提高了局部寻优能力和运算效率。【切入点】可见,将遗传算法应用于神经网络,使得神经网络中的连接权、网络结构和自学习能力得到进化[12],可保证全局收敛的同时,提高计算速度与精度[13]。
【拟解决的关键问题】本文采用人工神经网络结合遗传算法的策略对混流式水轮机转轮叶片几何参数进行多目标优化,并对比分析优化前后水轮机外特性、优化变量参数、转轮内部流场、转轮叶片压力分布及转轮无叶区、尾水管压力脉动幅值的变化规律,为转轮的多目标优化提供技术支撑。
1 叶片几何参数化
叶片几何参数化是多目标优化中较为关键的一步,转轮叶片在优化过程中常以CAD模型或三维离散点云等形式表达;本文由流道进口至出口流面线性插值出4个分流面,得到6个流面的叶片型线,并利用3次B样条插值曲面反算法,计算出控制点[14]。本文研究的混流式水轮机基本参数如表1所示。

表1 水轮机基本参数
2 转轮叶片多目标优化数学模型及求解
2.1 优化目标
本文以水轮机水力效率、空化性能以及水力稳定性作为优化目标,即降低转轮的水力损失、降低转轮空化系数以及降低转轮出口旋流数。其中,旋流数为转轮出口流体的周向动量与轴向动量之比[15],因此优化目标为minη()、minσ()、minSr()。基于以上条件,目标函数可定义为:
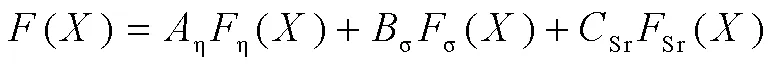
其中:
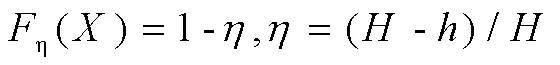
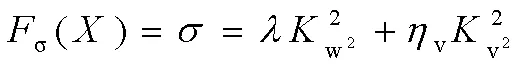
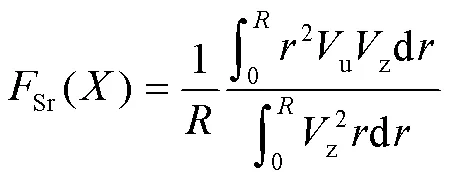
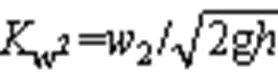
2.2 优化变量
转轮叶片进出口安放角不仅影响水轮机的性能,而且关系到叶道涡及叶片脱流等现象的产生[16];此外,叶片安装位置对转轮叶片所受载荷影响较大。因此,可通过对转轮叶片进出口安放角以及叶片安装角进行多目标优化。叶片的优化变量定义如下:
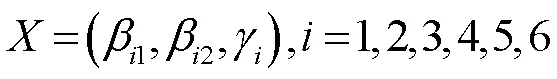
式中:为从上冠到下环的流面;1为不同流面的叶片进口安放角;2为不同流面的叶片出口安放角;为不同流面的叶片安装角。
2.3 优化约束条件
水轮机转轮优化包括3个方面,分别为能量约束、几何约束及变量约束[17],本文具体函数分别如下所示:
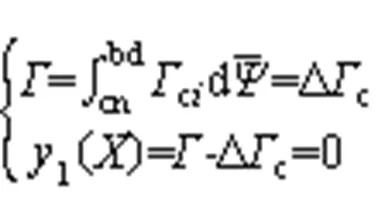
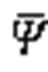
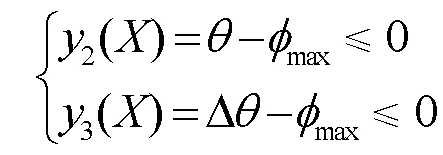
式中:max为叶片最大包角;Δ为上冠与下环的包角差。
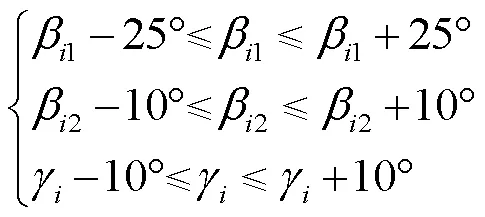
由于叶片进口安放角对水轮机水力性能的影响较大,因此适当加大进口安放角的优化搜寻范围。
2.4 叶片优化模型求解
叶片多目标优化需要足够的样本库,数据库既要保证样本数量足够多,足以覆盖优化参数的整个变化范围以保证得到全局最优解,又需尽可能减少样本量以减少计算量。因此,本文的样本数基于要求的折中方案设置为优化变量的2~3倍[18]。
据上文描述,优化变量为6个流面上的叶片安放角以及安装角共18个参数,为尽可能在有限的样本中获取更多的信息,本文采用FINE/Design3D中Database Generation模块的随机离散层取样方式(Random among Discrete Levels)生成样本。该方法在样本空间中抽取的样本点分布较均匀,全局性较强。本文基于该方法生成50个样本,且每个样本数据都包含了6个流面上共18个变量参数及其相应的流场计算结果。
本文采用人工神经网络模型建立优化目标与优化变量之间的非线性映射关系,设置其网络层数为3;为提高寻优能力并减少优秀个体的流失,采用遗传算法在求解空间内进行寻优,本文将初始种群设为100,种群重新生成循环次数设为60,设置迭代步数为50。
3 优化设计结果及分析
3.1 优化后叶片模型与原型对比
叶片优化前后在不同叶高处的型线对比如图1所示(其中红色代表优化前叶片,绿色代表优化后叶片)。从6个流面上的型线变化规律可以看出,优化后的叶片头部朝着叶片吸力面弯曲,表明优化后的叶片能适应更宽范围工况的工作状态;叶片优化前后各流面上的进出口安放角及叶片安装角如表2所示,从3个优化变量优化前后的变幅可得,叶片优化后的进口安放角变化较大,叶片优化前的进口安放角在S1—S5流面范围内均为负值,并且安放角的变化梯度较小;叶片优化后的进口安放角在S1—S4流面范围内为负,变化梯度较大,在S5—S6流面范围内安放角转为正值,意味叶片进水边靠下环处向叶片吸力面偏移,优化后叶片几何形状与X型叶片较为相似,表明优化后叶片具有更小的水力损失以及更广泛的工作范围等特点。
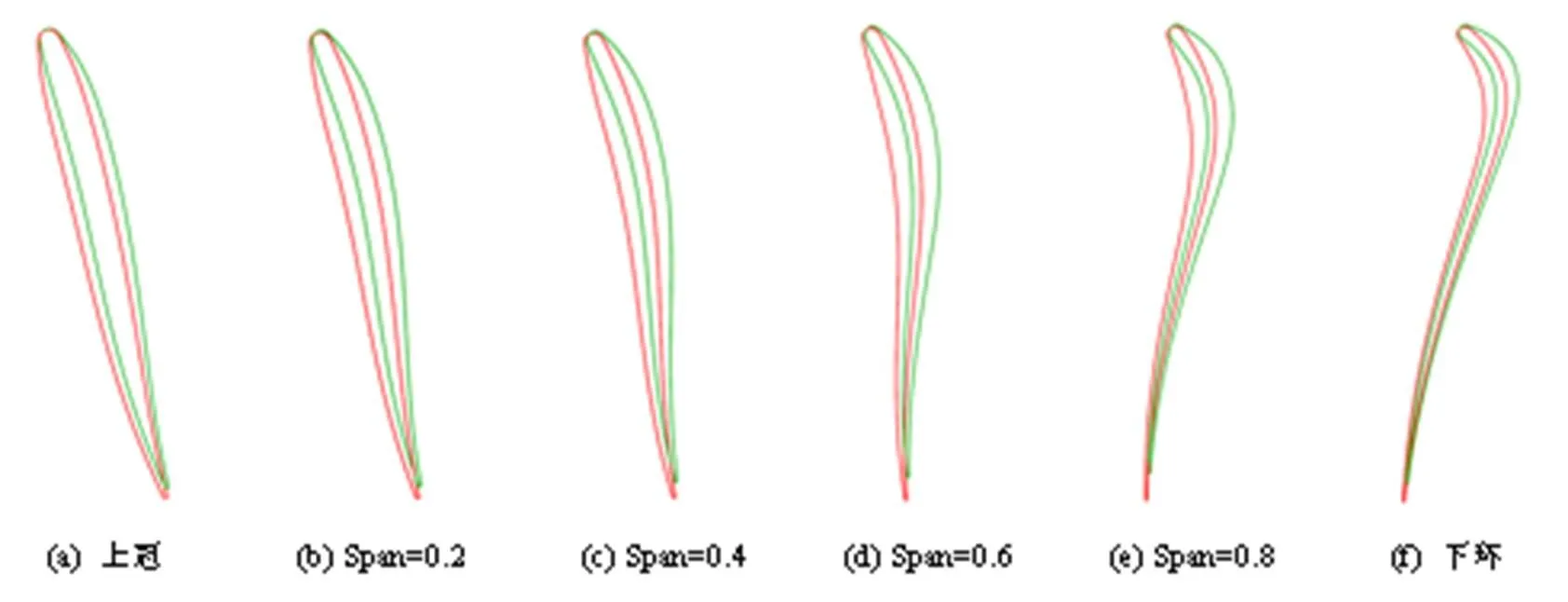
图1 优化前后叶片不同叶高处的型线对比

表2 优化前后优化变量对比
注1、2为进出口安放角,为叶片安装角,a为优化前,b为优化后。
3.2 外特性对比分析
叶片的效率和压力分布是衡量转轮性能好坏的重要参考依据。通过对电站的运行日志分析,得出该电站的实际运行水头处于高水头段。因此本文选取导叶开度为112°时运行水头分别为160、175、180 m的3个典型工况,分别命名为OP1、OP2、OP3。由于电站建设于20世纪,电站缺失部分运行监测设备,缺少蜗壳的进口流量及压力等重要数据。因此,电站实际运行水头、效率则通过运行日志中的上下游水位、机组的有功功率以及水轮机运转特性曲线和水轮机模型综合特性曲线推导得出(表3)。优化前后的效率及最低静压对比如表4所示。

表3 电站实际运行数据
对比表3、表4电站实际运行数据与全流道三维数值模拟结果,考虑实际运行数据的推导计算误差及数值模拟误差,数值模拟结果与实际数据较吻合,仿真数据较为真实。由表4可知,初始转轮效率随着出力的增加而增加,当达到设计工况时,转轮效率达到最大值;在超负荷工况运行时,转轮效率有下降的趋势;转轮优化后效率的变化趋势与优化前相同,且优化后3个工况下的转轮效率均有小幅度提升,表明优化后转轮拓宽了叶片工作的高效区[19]。此外,优化后的叶片最低静压均得到大幅度提升,其中超负荷工况的静压增长幅度最大,转轮抗空蚀性能明显提升。

表4 优化前后的效率及最低静压对比
3.3 稳态流场分析
3.3.1转轮流道速度矢量图
叶片优化前后3个工况下的转轮流道速度矢量如图2所示。由图可得,叶片优化前进口速度较小,叶片头部出现明显的不稳定旋涡及回流现象,阻塞了水流流动,使得叶片对水头大变幅运行工况不适应,从而导致叶片表面易出现脱流、旋涡等现象。该现象凸显了优化前转轮叶片的设计不合理;通过对叶片各流面的进口安放角进行优化,由图可得,优化后叶片在3个工况下的进口流速均明显增高,速度矢量分布相比优化前更为均匀。表明优化后叶片降低了转轮流道中出现旋涡、二次回流等现象的可能性,提高了流动的稳定性,表明优化后的叶片较优化前更适应当前机组运行工况。
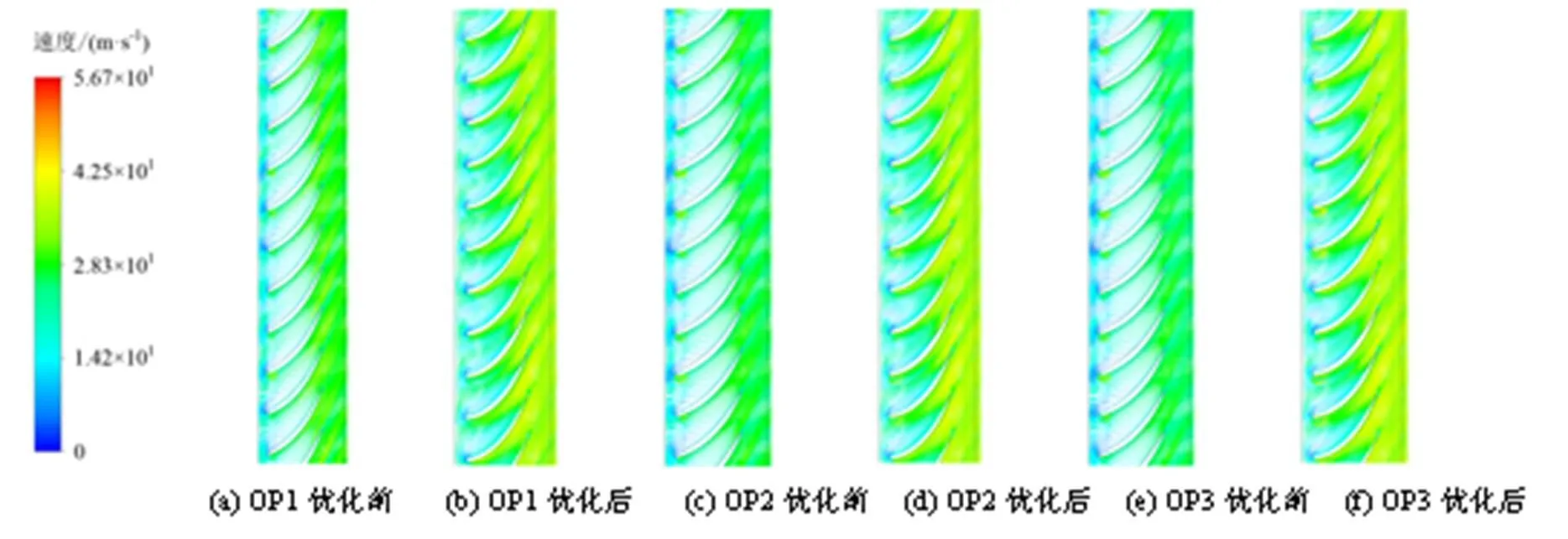
图2 转轮流道速度矢量图
3.3.2叶片表面静压对比
优化前后的叶片吸力面静压对比如图3所示。优化前叶片头部在3个工况下均出现明显的负压区,随着运行负荷的提升,负压区从头部靠下环处朝上冠扩大;优化后叶片负压区消失,表明本次优化有效改善了3个工况下转轮叶片的进口压力,保证转轮叶片在实际运行中具有较好的空化性能。
3.3.3压力分布曲线
翼型空蚀是混流式水轮机转轮最主要的空蚀现象,优化前后叶片在3个工况下0.5倍叶高处的压力分布如图4所示。由图4(b)、图4(c)可得,初始转轮叶片进口处有明显负压,其压力值远低于常温下的汽化压力,优化后叶片进口压力有较大涨幅;优化后叶片在3个工况下的压力面与吸力面上的压力均有较小涨幅,压力随相对弦长变化规律一致,表明叶片优化后表面无较大的压力波动,有效提高了叶片抗空蚀的能力。
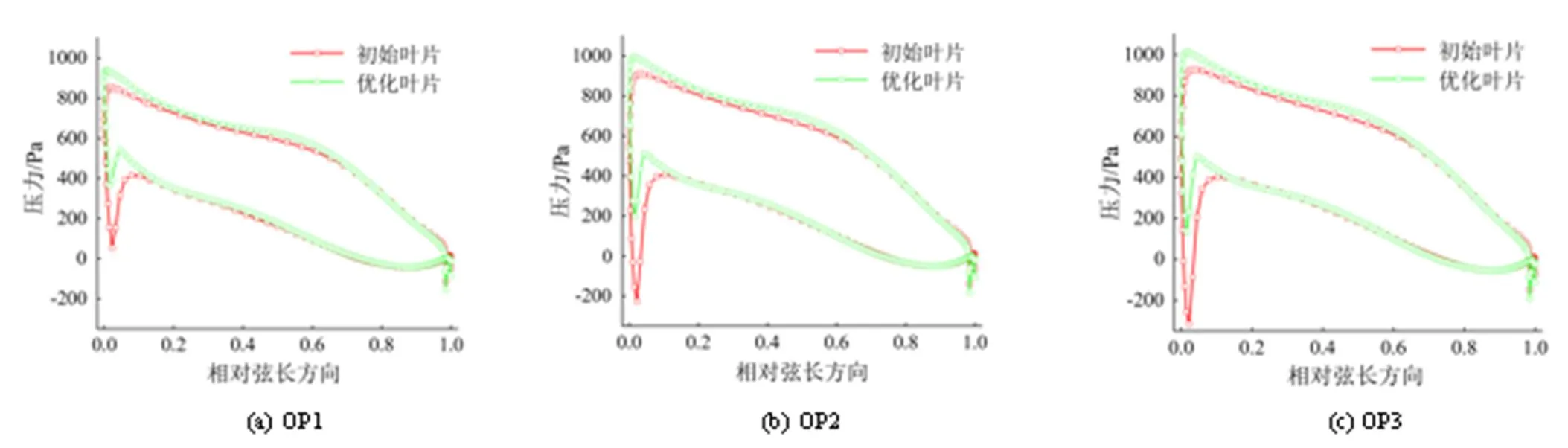
图4 叶片0.5倍叶高处压力分布曲线
3.4 压力脉动分析
由于转轮与活动导叶之间动静干涉、转轮出口流体与尾水管的干涉现象剧烈,造成能量损失,本文在活动导叶与转轮区域间、尾水管锥管段设置相应监测点。监测点V1—V36均匀分布在转轮叶片0.5倍叶高处无叶区,W1、W2为尾水管锥管段处的监测点,监测点具体位置见图5。
3个工况下无叶区周向相对压力脉动幅值如图6所示。叶片优化后在3个工况0.5倍叶高处无叶区的周向相对压力幅值显著降低,相对幅值的变化趋势较优化前更均匀,表明叶片优化后无叶区动静干涉对机组的扰动明显减小。
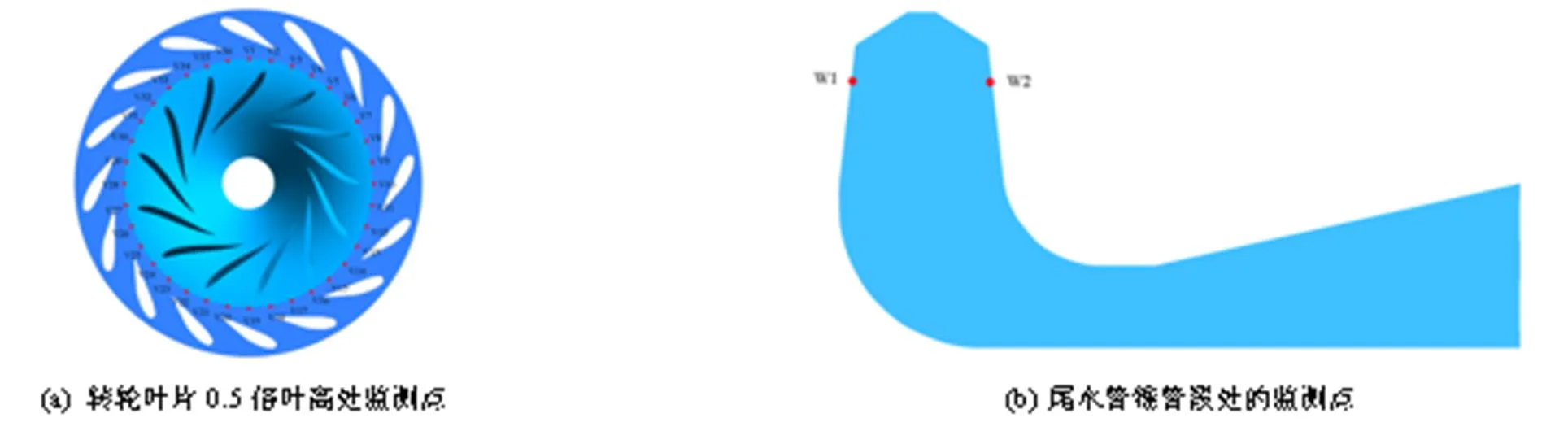
图5 压力脉动监测点
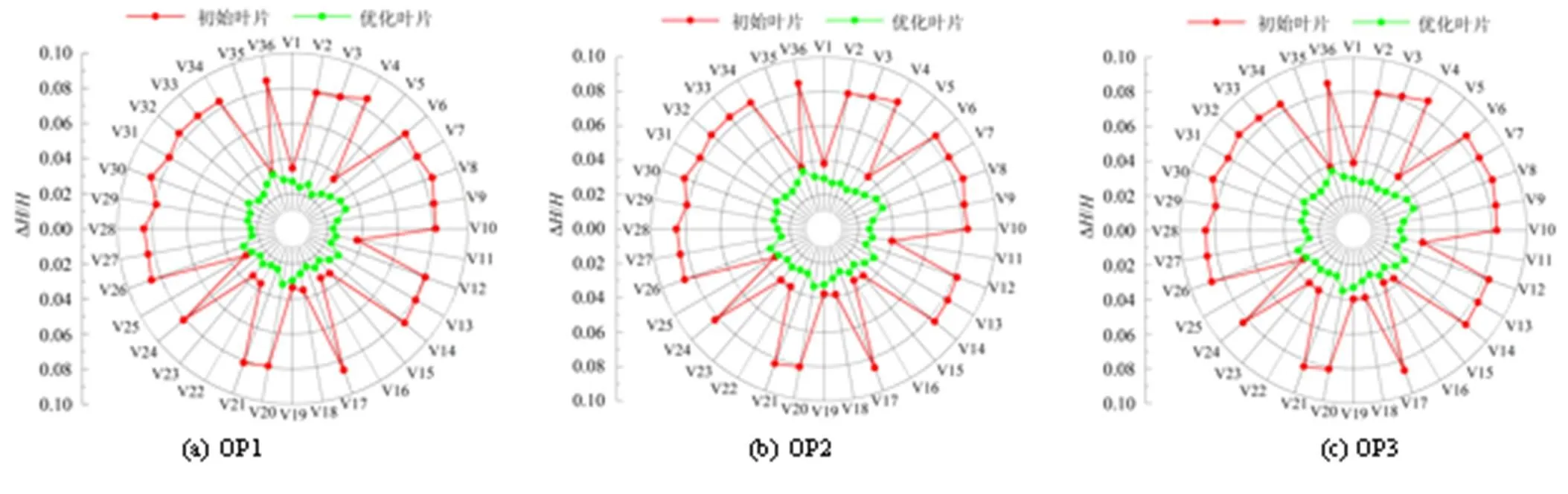
图6 无叶区周向相对压力脉动幅值
图7(a)、图7(b)与图7(c)、图7(d)分别为转轮叶片优化前后在3个工况下尾水管监测点W1、W2的压力脉动时域图与频域图。由时域图可得,监测点W2的压力波动值、压力脉动强度高于监测点W1,叶片优化后尾水管锥管段处的压力值均显著降低;由频域图可知,2个监测点的压力脉动幅值均在130 Hz达到最大,该频率为转轮的通过频率。在通过频率下,叶片优化后监测点W1测得的压力脉动幅值为优化前叶片的0.71倍,监测点W2测得的压力脉动幅值为优化前叶片的0.66倍。由于尾水管涡带的影响;3个工况下均监测到单倍转频的脉动信号,其脉动幅值较小,优化后的尾水管流场更稳定。
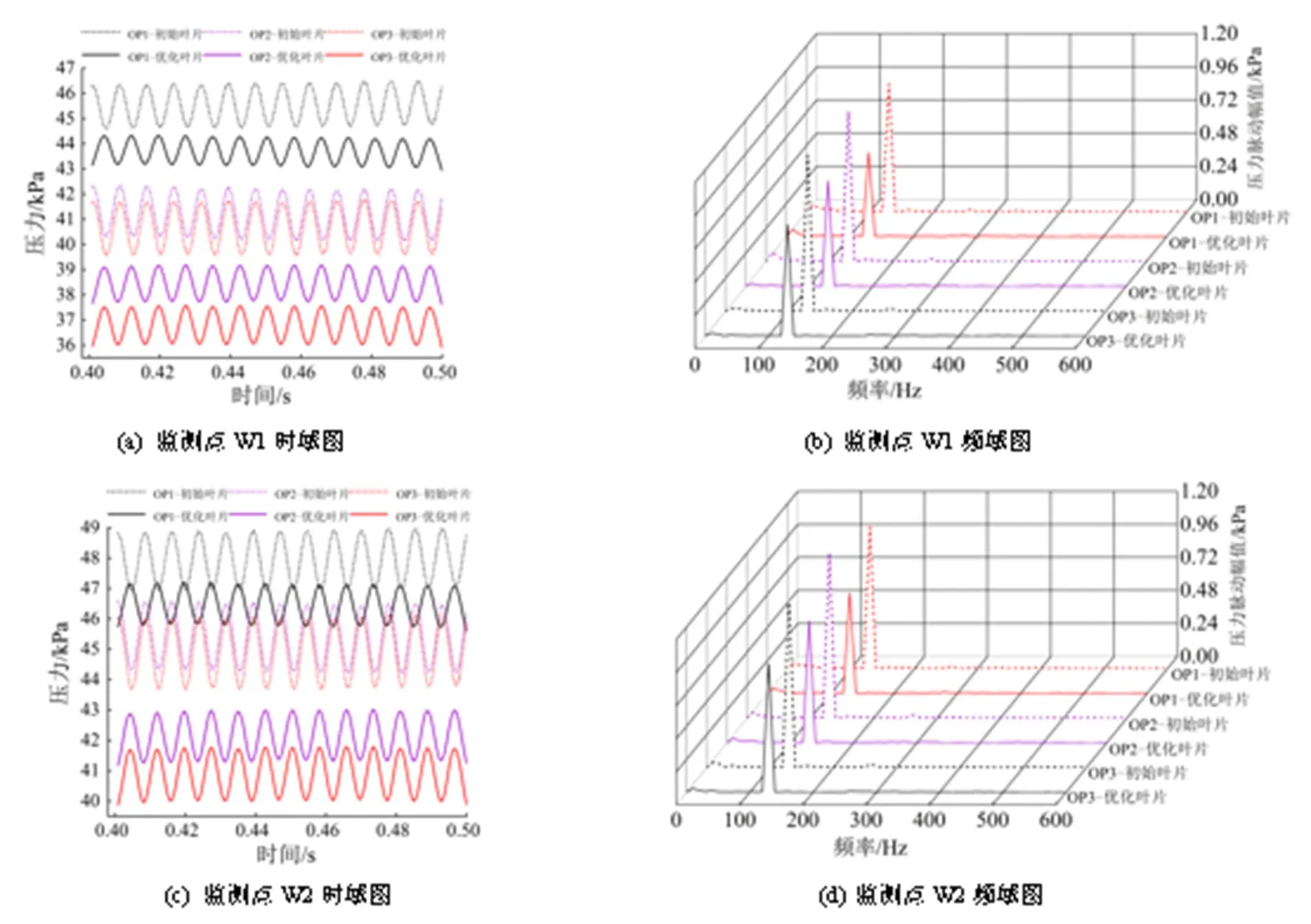
图7 尾水管压力脉动时域图与频域图
4 讨论
对于转轮的多目标优化而言,许多参数彼此相互制约、相互关联,确定独立的优化变量较为复杂。为此,首先参考其余叶片式流体机械的多目标优化变量,找到影响转轮叶片性能的主要变量。由于叶片进出口安放角对水轮机外特性如效率、空化、振动等影响较大,通过优化叶片进出口安放角以改善混流式水轮机的能量特性这一方法具有较强的普适性。本文针对某电站混流式水轮机转轮叶片进口边局部压力过低易发生空化的问题,选择叶片进出口安放角作为优化变量,通过随机离散抽样的方法生成计算样本,并利用CFD数值计算得到样本的性能参数,进而采用人工神经网络模型建立转轮效率、空化系数、转轮出口旋流数与优化变量的映射关系,最后利用遗传算法对叶片的几何参数寻优并对比分析转轮叶片优化前后混流式水轮机的性能变化。
研究表明,叶片优化后头部静压值明显提升,提升了3个工况下的转轮效率,与田锋社[6]的研究结果相似,但田锋社的研究结论中叶片头部静压无较大提升,可能由于本文中的优化前叶片设计不合理使得优化效果相比于前人研究更明显;以转轮出口旋流数作为优化目标可明显降低转轮无叶区的压力脉动幅值,与唐健[17]的研究结论一致。表明以转轮出口旋流数作为优化目标,对于降低动静干涉引起的不稳定性的优化效果较好。
由于人工神经网络具有高度的自组织、自适应的能力,以及遗传算法具有易于实现、应用效果显著的优点而逐渐应用于水力发电行业中,以往很多学者在确定转轮的优化变量时,会考虑上冠、下环轴向长度,下环进出口直径等几何参数。在进行水轮机改造时,一般不可能对埋入部件进行较大的改造,因此不适用于本文提到的待改造优化的老电站,本文结合电站实际改造优化需求,保证流道尺寸不变的约束条件,实现优化转轮与原其余过流部件的匹配优化。
本文采用人工神经网络结合遗传算法的策略对叶片几何参数进行多目标寻优,较大程度上提高了寻优的速度与精度。由于机组运行工况范围较大,同时优化更多运行工况会导致计算时间过长并且难以收敛,因此该方法尚存在一定局限性。本文的多目标优化只是针对单一的转轮叶片而没有考虑多级优化,多级优化将增加优化变量的个数,优化过程将更难收敛或陷入局部最优解,后续将对水轮机其余部件如蜗壳、固定导叶、活动导叶、尾水管等部件进行协同优化可行性的研究。
5 结论
1)优化后叶片头部靠下环处有朝叶片吸力面后掠的趋势、在OP1、OP2、OP3工况下效率分别提升了0.22%、0.56%、0.60%;优化后叶片的空化性能得到提升。
2)叶片优化后的转轮流道内速度矢量更加均匀,叶片进口旋涡、回流现象明显减少;无叶区周向相对压力脉动幅值约为叶片优化前的0.5倍,尾水管锥管段压力脉动幅值约为原先0.7倍,有效提升了机组的运行稳定性。
3)通过对混流式转轮叶片进行多目标优化,最终得到了满足综合性能的叶片模型,验证了基于人工神经网络的遗传算法的策略优化混流式水轮机叶片的可行性。
(作者声明本文无实际或潜在的利益冲突)
[1] 何芳. 混流式水轮机转轮结构及优化设计[D]. 南昌: 南昌大学, 2008.
HE Fang. Francis turbine runner design and optimization of the structure[D]. Nanchang: Nanchang University, 2008.
[2] 刘安然. 基于数值方法的混流式水轮机转轮优化设计[D]. 邯郸: 河北工程大学, 2014.
LIU Anran. Francis turbine runner design optimization based on the numerical method[D]. Handan: Hebei University of Engineering, 2014.
[3] 刘小民, 张文斌. 采用遗传算法的离心叶轮多目标自动优化设计[J]. 西安交通大学学报, 2010, 44(1): 31-35.
LIU Xiaomin, ZHANG Wenbin. Multi-objective automatic optimization design of centrifugal impeller based on genetic algorithm[J]. Journal of Xi’an Jiaotong University, 2010, 44(1): 31-35.
[4] 吴晓冬, 赖喜德, 杨洪忠. 基于多工况数值试验的水轮机改造优化设计技术[J]. 西华大学学报(自然科学版), 2008, 27(6): 6-8, 12, 120.
WU Xiaodong, LAI Xide, YANG Hongzhong. Optimization design technique for retrofit of hydro turbines based on multi-condition numerical test[J]. Journal of Xihua University (Natural Science Edition), 2008, 27(6): 6-8, 12, 120.
[5] 区天庆. 中小型水电站水轮发电机组的技术改造[J]. 技术与市场, 2011, 18(7): 228-229.
[6] 田锋社. 八盘峡电站D179a转轮的多目标优化设计[J]. 西北水电, 2004(4): 46-48.
TIAN Fengshe. Multipurpose optimal design of D179a runner for Bapanxia Hydropower Station[J]. Northwest Water Power, 2004(4): 46-48.
[7] 朱国俊, 冯建军, 郭鹏程, 等. 基于径向基神经网络-遗传算法的海流能水轮机叶片翼型优化[J]. 农业工程学报, 2014, 30(8): 65-73.
ZHU Guojun, FENG Jianjun, GUO Pengcheng, et al. Optimization of hydrofoil for marine current turbine based on radial basis function neural network and genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(8): 65-73.
[8] 赵斌娟, 仇晶, 赵尤飞, 等. 双流道泵蜗壳多目标多学科设计优化[J]. 农业机械学报, 2015, 46(12): 96-101, 225.
ZHAO Binjuan, QIU Jing, ZHAO Youfei, et al. Multi-objective and multidisciplinary optimization of double-channel pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 96-101, 225.
[9] 杨洪忠, 赖喜德, 张仁福. 水电站水轮机改造中的新技术[J]. 四川工业学院学报, 2004, 23(S1): 175-177.
YANG Hongzhong, LAI Xide, ZHANG Renfu. New techniques for rehabilitation of hydro turbines of hydro power plant[J]. Sichuan University of Science and Technology, 2004, 23(S1): 175-177.
[10] 叶道星, 李浩, 马秋妍, 等. 采用近似模型和NSGA-Ⅱ遗传算法的旋流泵性能优化研究[J]. 灌溉排水学报, 2019, 38(7): 76-83.
YE Daoxing, LI Hao, MA Qiuyan, et al. Optimal design of vortex pump using approximate model and the non-dominated sorting genetic algorithm[J]. Journal of Irrigation and Drainage, 2019, 38(7): 76-83.
[11] 王掩刚, 魏崃, 陈为雄. 大弯角串列叶型优化设计与数值分析[J]. 推进技术, 2014, 35(11): 1 469-1 474.
WANG Yangang, WEI Lai, CHEN Weixiong. Optimization and numerical simulation of high-turning tandem cascade[J]. Journal of Propulsion Technology, 2014, 35(11): 1 469-1 474.
[12] 李雪, 刘长发, 朱学慧, 等. 基于BP人工神经网络的海水水质综合评价[J]. 海洋通报, 2010, 29(2): 225-230.
LI Xue, LIU Changfa, ZHU Xuehui, et al. Integrated assessment of sea water quality based on BP artificial neural network[J]. Marine Science Bulletin, 2010, 29(2): 225-230.
[13] 苏林, 祝云. 基于粒子群算法的柬埔寨桑河水电站调度优化研究[J]. 电力设备管理, 2021(7): 90-92.
SU Lin, ZHU Yun. Research on scheduling optimization of Cambodia’s Sanhe Hydropower Station based on particle swarm optimization[J]. Electric Power Equipment Management, 2021(7): 90-92.
[14] 赵林明. 水轮机数学模型[M]. 北京: 中国水利水电出版社, 2011.
ZHAO Linming. Mathematical model of hydraulic turbine[M]. Beijing: China Water & Power Press, 2011.
[15] SUSAN-RESIGA R, MUNTEAN S, HASMATUCHI V, et al. Analysis and prevention of vortex breakdown in the simplified discharge cone of a francis turbine[J]. Journal of Fluids Engineering, 2010, 132(5): 1.
[16] 刘胜柱, 罗兴錡, 纪兴英, 等. 叶片几何参数对水轮机稳定性的影响[J].水力发电学报, 2004, 23(1): 91-96.
LIU Shengzhu, LUO Xingqi, JI Xingying, et al. Effect of blade geometric parameters upon hydraulic turbine stability[J]. Journal of Hydroelectric Engineering, 2004, 23(1): 91-96.
[17] 唐健. 基于流面上叶型自动逼近的高水头混流式转轮水力优化设计[D]. 成都: 西华大学, 2016.
TANG Jian. Research on hydraulic optimization design of francis runner based on automatic approximation of blade profiles on stream-surface[D]. Chengdu: Xihua University, 2016.
[18] 郭然, 贾力平, 樊小莉. NUMECA系列教程[M]. 北京: 机械工业出版社, 2013.
GUO Ran, JIA Liping, FAN Xiaoli. NUMECA series tutorial[M]. Beijing: China Machine Press, 2013.
[19] 姜劲. 基于遗传算法的竖轴潮流能水轮机性能优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
JIANG Jin. Optimization study on tidal currnet turbine performance based on genetic algorithm[D]. Harbin: Harbin Engineering University, 2008.
Using Artificial Neural Network to Solve Multi-objective Optimization of Francis Turbine Runner
WANG Rongtao, LAI Xide*, CHEN Xiaoming
(Xihua University, School of Energy and Power Engineering, Chengdu 610039, China)
【Background】Technical renovation of turbine equipment in hydropower plant has attracted increased attention due to its low investment, quick return and high economic benefit. The purpose of modifying turbine equipment in hydropower station is to increase its capacity or improve its operation performance. Generally, it is impossible to make large modification to embed components in turbine modification. Most modifications aimed at the runners or the guide vanes. It is important to study effective multi-objective runner optimization design method to ensure efficiency, cavitation performance and hydraulic stability of the unit, as well as the comprehensive performance of the unit under different operating conditions.【Objective】This paper is to explore an optimization method which can simultaneously improve the operation efficiency, cavitation performance and operation stability of the Francis turbine, and provide a technical approach for multi-objective optimization of the Francis turbine runner.【Method】Taking the position angle and installation angle of runner blade inlet and outlet as optimization variables, the sample database was obtained by random discrete sampling of blade geometry parameters. The performance parameters of each sample were obtained based on CFD numerical calculation. A multi-objective function was then established, considering runner efficiency, swirl numbers at the outlet and cavitation coefficient of the Francis turbine. The mapping relationship between optimization variables and the multi-objective function is established based on artificial neural network. Runner blades with18 geometric parameters are optimized by genetic algorithm, and the performance of the runner blades before and after optimization is compared and analyzed. 【Result】For guide vane opening 112 degrees with running head being 160 m, 175 m or 180 m, the optimized runner efficiency was increased by 0.22%, 0.56% and 0.60% respectively compared with that without optimization. The optimization also improved the pressure distribution in the blades, and reduced pressure fluctuation amplitude at the vaneless area of the runner and the conical section of the draft tube.【Conclusion】The greater the optimized blade inlet placement angle was, the greater the improvement of comprehensive performance of Francis turbine would be.
francis turbine; runner; multi-objective optimization design; artificial neural network; genetic algorithm
1672 - 3317(2023)09 - 0046 - 07
TV734.1
A
10.13522/j.cnki.ggps.2022588
王荣涛, 赖喜德, 陈小明. 基于人工神经网络模型的混流式水轮机转轮多目标优化[J]. 灌溉排水学报, 2023, 42(9): 46-52.
WANG Rongtao, LAI Xide, CHEN Xiaoming. Using Artificial Neural Network to Solve Multi-objective Optimization of Francis Turbine Runner[J]. Journal of Irrigation and Drainage, 2023, 42(9): 46-52.
2022-10-21
2023-05-19
2023-09-14
四川省科技计划项目(2020ZHCG0018,2021JDZH001,2022JDZH0011)
王荣涛(1997-),男。硕士研究生,主要从事流体机械研究。E-mail: 2956014578@qq.com
赖喜德(1962-),男。教授,主要从事流体机械研究。E-mail: laixd@mail.xhu.edu.cn
@《灌溉排水学报》编辑部,开放获取CC BY-NC-ND协议
责任编辑:赵宇龙
