一种基于混沌置乱和图像融合的信息隐藏算法研究

蔡正保

(1.安徽大学计算机科学与技术学院,安徽 合肥 230601;2.安徽国防科技职业学院信息技术学院,安徽 六安 237011)

0 引言

在信息技术快速发展的大环境下,用户可以便捷地共享数字媒体信息,数字媒体的安全问题倍受人们重视。数字图像简单且直观,同时包含丰富的亮度、纹理等信息,在生产生活中常常被选作信息交流的媒介[1]。然而,因特网中大量的图像数据传输以及交互引起了诸如非法篡改、隐私泄露等众多复杂问题,若得不到妥善处理会引起一系列不良后果[2]。若采用常用的图像隐藏算法对秘密图像进行简单隐藏,黑客很可能利用现有的攻击手段提取出秘密图像。因而,采用常规、普通的算法对秘密图像进行隐藏很可能不是一个好的方案[3]。还需要进一步寻找、探索新的信息隐藏算法。本文探索了一种采用混沌置乱技术和图像融合技术相结合的方法对秘密图像进行隐藏。

1 混沌置乱

混沌系统具有对初始值以及参数的不可预测性、敏感性、遍历性、类白噪声性等优良特性,经常被用于信息隐藏领域。混沌系统运用初值能够精确地重构混沌序列[4],这与密码学的一些相关研究高度关联。混沌映射能够生成没有规则的混沌序列,可以运用混沌映射后获得的混沌序列来对图像的像素进行无规则分布,获得图像像素的无序排列。这种经过混沌排列后的图像像素随机分布,呈现出混沌特性,可称作图像的混沌置乱[5]。混沌序列在信息隐藏技术中的主要用途有:增加破解难度,提高算法的安全性;对于脆弱性算法,造成脆弱性隐体被攻击后提取失败;有利于分散突发错误[6]。

Logistic映射是一种应用比较普遍的混沌系统,Logistic混沌序列能够呈现出优良的随机性、复杂性以及相关性,也就是对混沌序列进行准确预测似乎不具备可能性[7]。其系统方程可描述为如公式(1)的形式:

(1)

在μ取值为2时,Logistic映射模型将全部呈现混沌现象,能覆盖[-1,1]的范围,遍历特性明显,最具有混沌性质。所以,可直接将μ取值为2,便可获得Logistic映射的简化公式,如公式(2)所示:

(2)

把公式(2)参照二次方程的形式进行改进,此时,xn为变量,而xn+1为参数,可以推导出方程的两个解,如公式(3)和(4)所示:

(3)

(4)

要想从xn+1推导出其前一个值,会有两种可能的数值,并且这两个数值的正负符号相反。在这种情况下,若在每一次迭代过程中记下当时值的符号,在逆运算时便能够在两个解中挑选出正确的解,符号用S来记录。此时,对于x,可有公式(5):

(5)

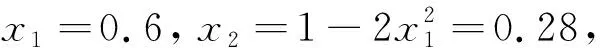
图1 混沌置乱加解密原理

依据以上思路,将数字图像的某种信息作为以上算法的初始值,进行迭代运算,便可对图像信息加密。本文将秘密图像的低频分量和高频分量系数作为Logistic映射的初始值来对秘密图像进行混沌置乱。

2 图像融合

图像融合是把两个或者两个以上的数字图像进行信息提取并融合到一个图像中,如军事融合图像的安全传输、医学融合图像的网络传输与遥感融合图像的信息传输等特殊应用[8]。图像融合和图像加密在诸多应用中有着紧密的联系,将二者有机地结合起来可以有效地提高数据处理效率,增强数据传输的安全性[9]。

由于现代生产生活中信息量和信息复杂度都比较大,使用传统方法不能很好地处理这些信息量,需要探索新方法、新技术,或者优化传统方法。最终找到一个合理的方法或技术,运用多种资源来分析处理这些信息,从而使得目标图像能够更加完整、清晰地显示出来[10]。

在分析已有文献[11-12]所述的图像隐藏方法的基础上,采用一种图像隐藏效果较好的算法。

对于邻域Q,能够定义出待融合图像以(j,k)作为中心点的窗口能量计算公式:

(6)

其中,l为小波分解尺度,V表示原始载体图像P和需要隐藏的秘密图像y;Gl,V(j,k)是载体图像P或秘密图像y在尺度l方向以(j,k)作为中心点的小波系数值。

(2)低频分量融合。对于图像P、y的低频分量DP、Dy的全部元素信息,统计出来其3×3的邻域能量WP(j,k)、Wy(j,k),再做归一化处理,如公式(7)和(8)所示:

(7)

(8)

进行归一化,得出邻域能量,再依据公式(9)进行融合:

H(j,k)=WP×DP(j,k)+Wy×Dy(j,k).

(9)

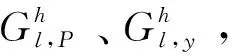
(10)

其中,V表示载体图像P或秘密图像y;h=X,Y,Z,其中,X、Y、Z分别表示垂直、水平、对角三个方向上的高频分量。

(11)

(4)低频和高频系数小波重构。小波重构是关键一环,把通过融合获得的低频和高频系数做小波重构操作,便可以输出最终的融合图像。

3 基于混沌置乱和图像融合的信息隐藏算法

3.1 图像隐藏

选用的载体图像为P,待嵌入的秘密图像为y,P和y均为数字图像。

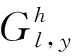
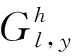
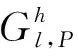
(5)小波重构。把通过融合所获得的低频和高频系数做小波重构操作,便可以输出最终的融合图像。

图像隐藏算法的详细流程如图2所示。

图2 图像隐藏算法流程

3.2 图像恢复

图像恢复主要是秘密信息的提取,其算法与图像隐藏算法互为逆运算。

(1)小波分解。此时的融合图像P′也就是含密图像,对含密图像进行小波分解操作,获得低频和高频系数。

(2)高频分解。对高频系数进行分解,获得载体图像的高频分量和秘密图像的混乱高频分量。

(3)低频分解。对低频系数进行分解,获得载体图像的低频分量和秘密图像的混乱低频分量。

(4)去乱。对秘密图像混乱的高频分量和低频分量进行去乱处理,得到去乱后的高频分量和低频分量。

(5)小波重构。对秘密图像的高频分量和低频分量进行三层小波重构,获得秘密图像信息,即提取出秘密图像。

图像提取算法的详细流程如图3所示。

图3 图像提取流程

4 仿真和讨论

运用MATLAB软件来仿真本文的图像隐藏算法,根据实验结果对算法的各项数据进行评价。为检验算法的各项性能指标,选取两幅256×256灰度图像Lena、cameraman作为载体图像;选用两幅128×128灰度图像boat、airplane作为秘密图像;再将两个秘密图像分别嵌入载体图像。实验的原始图像及结果图像如图4和图5所示。

图4 载体图像Lena和秘密图像boat及其实验结果

图5 载体图像cameraman和秘密图像airplane及其实验结果

为验证本文算法的优劣,这里运用了文献[11]、文献[12]所述算法对图像进行了隐藏,并对运用三种方法隐藏秘密图像所得的实验数据进行记录(表1)。表1中峰值信噪比(PSNR)数据验证了三种方法对图像进行隐藏后肉眼不能感知载体图像的变化,而本文所述的算法相较于另外两种算法更胜一筹。

表1 肉眼不能感知载体图像失真的实验数据

为了更好地检测本文算法、文献[11]算法、文献[12]算法对载体图像造成的影响,可采用更多的图像评价指标进行实验验证。这里参照统计学失真标准对图像进行统计、计算,运用信息熵、平均值和标准差这三个图像评价参数来比较载体图像和含密图像的前后变化,仿真实验数据如表2所示。根据表2的数据统计得出,使用本文算法处理后的载体图像和含密图像的前后评价参数变化很小,比另外两种算法对载体图像自身的影响更小。

表2 载体图像和含密图像的图像参数

从图4和图5的图像实验结果以及表1和表2的仿真实验数据可以得出,综合运用混沌置乱和图像融合的隐藏算法提高了算法本身的安全性能,在实际应用中可以很好地保证含密图像的视觉效果,使秘密图像的隐藏效果也较好。

对于算法鲁棒性的检测,可以在仿真实验中对含密图像做任意涂改、加入椒盐噪声、剪切等处理操作。图6、图7、图8分别展示了受到任意涂改、加入2%椒盐噪声、12.5%剪切这三种常规图像攻击后的含密图像以及提取出的秘密图像。

图6 任意涂改攻击的图像

图7 加入2%椒盐噪声攻击的图像

图8 12.5%剪切攻击的图像

从图6、图7、图8可以看出,本文算法在遭受以上几种常见的攻击后,从含密图像中依然能够提取出较为清晰的秘密图像。

同样,对文献[11]、文献[12]所述算法在受到几种攻击情况下进行了实验仿真,并将三种算法所得的实验数据进行记录(表3)。由表3看出本文算法的归一化相关系数NC值较大,由此验证了本文算法能较好地应对上述三种常见图像攻击,鲁棒性好,相对于同类算法有一定的优越性。因此,运用基于混沌置乱和图像融合的信息隐藏算法进行仿真实验,能够获得较好的实验结果。

表3 各种攻击的客观评测结果

5 结语

本文所述的信息隐藏算法,将原始载体图像和待隐藏的秘密图像做小波分解操作,得到各自的高频、低频分量,把秘密图像的高频、低频分量分别进行混沌置乱,再与载体图像的高频、低频分量进行图像融合运算,得到高频系数和低频系数;将高频系数和低频系数进行小波重构,获得含密图像,完成对秘密图像的隐藏。对算法进行实验验证和仿真操作,得到具体图组和仿真实验数据。采用混沌置乱技术对秘密图像高频、低频分量进行预处理,可以大幅度提高秘密图像的安全性,运用图像融合的方法可以输出一幅更易于人类视觉感知、方便计算机处理分析的优质图像,进一步提高算法的抗攻击能力。

基于混沌置乱和图像融合的信息隐藏算法具有失真度小、不可见性和安全性高以及在面对常见图像攻击鲁棒性好的特点。但也存在数据处理比较慢等缺陷,有待于在现有研究基础上进一步改进。随着信息隐藏技术的发展,国内外对混沌置乱和图像融合技术的研究也将逐步深入。