有高程数据库支持的弹道预警信息生成方法

杨 冬 徐 劲 杜建丽

（1 中国科学院紫金山天文台 南京 210023）

（2 中国科学院空间目标与碎片观测重点实验室 南京 210023）

1 引言

弹道导弹预警在航天技术和战略预警中具有广阔的应用前景, 正日趋成为国内外研究的热点课题. 弹道导弹的整运行过程分为助推段、中段和再入段三部分. 其中中段又叫自由飞行段, 是弹道导弹关闭发动机后在大气层外飞行的过程, 这个阶段飞行时间最长, 占整个弹道飞行时间的80%以上,且仅受自然力影响, 其轨道特征容易被掌握. 因此中段是各种无线测量设备进行捕获、跟踪、身份鉴别、计算预警信息（如发、落点时间、位置）的主要阶段.

在此前的研究中, 弹道导弹中段的身份鉴别和发、落点信息推算是两个不同的课题. 文献[1–3]等都基于弹道导弹弹头在雷达回波下反映出的物理特征, 例如弹头的微动（如进动、章动、雷达散射截面（Radar Cross Section, RCS）的变化）存在周期性特点, 可通过雷达回波呈现的微多普勒效应进行分析和识别; 又例如雷达对飞行目标进行的高分辨率一维成像（High Resolution Range Profile, HRRP）具有成像速度快、分辨率高的特点,且HRRP能提供沿雷达视线方向强散射中心的分布信息, 具有目标的结构特征, 根据获取的特征和目标特征库的模板对比, 即可完成目标身份鉴别.而关于发、落点信息推算的研究都是在已知目标为弹道导弹的前提下, 利用弹道与地球有交点这一特点进行推算. 推算方法多是如文献[4]介绍的使用卡尔曼滤波或改进的卡尔曼滤波对目标运动方程进行外推的方法进行计算. 这类外推方法本质上是一种试探法, 即每一次外推结束后需要判断是否进入地球内部, 如果进入地球内部则需采用二分法反复外推最终求得结果. 其计算效率与滤波步长的选取密切相关, 最合适的滤波时间步长又与具体的弹道有关, 导致很难有普适的最优步长可供选择. 此外这种方法未考虑目标在飞行时受到的摄动力, 也没有加入高程信息的支持. 也有文献提出把导弹轨道简化为二体模型下的椭圆轨道后通过几何关系求解弹道与地球交点[5], 但这种方法同样没有考虑摄动因素和高程的影响. 文献[6]则另辟蹊径, 根据导弹轨道与地球有交点, 而卫星轨道与地球无交点这一特征, 提出了一种同时进行快速鉴别目标身份和生成预警信息的方法. 该方法计算速度快、处理过程简单稳健、计算效率高, 且考虑了地球对目标的主要摄动项. 但在使用该方法生成预警信息时,地球被粗略地简化为一个参考椭球体, 高程信息依然被略去. 这样虽然减少了计算量、提高了计算速度, 但是如果导弹的发点或落点位于高山、高原等地表与参考椭球面距离较大的地区, 使用该方法会降低预警信息的精度, 且高程值越大, 精度降低得显然也就越多. 因此有必要改进文献[6]介绍的预警信息推算方法, 使新的方法在保持较高计算效率和稳健、稳定度的前提下尽量消除高程因素引起的误差, 提高预警信息的精度. 本文将针对这一问题展开理论分析和探讨.

用于支持发、落点推算的高程信息库可使用全球数字高程模型（Digital Elevation Model,DEM）, 它是对地球表面地形地貌的一种离散数学表达. DEM的原理是将一片区域划分为b行c列（b、c均为正整数）的四边形, 计算每个四边形的平均高程, 然后以三维矩阵的方式存储这些平均高程. 用函数的形式可描述为:

式中,Lj、ψj是大地经纬度坐标,Hj是经纬度坐标（Lj,ψj）处的高程. 目前常见的高分辨率全球DEM的生成主要得益于全球卫星遥感、卫星测高、船载测深等资料的获取[7]. 一般来说, DEM里小四边形的边长就是DEM的分辨率. 常见的分辨率有90 m、30 m、12.5 m、5 m等. 分辨率是描述地形精确程度的一个重要指标, 边长越小同一片区域分割的四边形越多, 这就意味着分辨率越高, 描述地形越精确.

2 弹道导弹预警的原始方法

为了后续阐述方便, 简要介绍一下文献[6]提出的方法. 当导弹处于发点或落点时, 其所处的弹道位置与地球表面相交, 导弹地心距r（f）与其星下点地心距R（f）相等, 即

其中f为目标于t时刻的真近点角. 求解（1）式的方法就是通过轨道运动特点鉴别目标身份和推算预警信息的核心内容,f有解就证明目标与地球有交点, 通过轨道根数就能够推算出发、落点等预警信息. 直接求解（1）式难度较高, 因此使用两个步骤迭代求解: 第一步迭代是在二体运动模型下求解初始值. 迭代初值是由初始根数求得的目标真近点角f0, 收敛需要满足的判定门限为|rk-Rk|<ε, 其中|rk-Rk|是第k次迭代后,目标地心距与星下点地心距之差的绝对值,ε >0是收敛门限,k表示第k次迭代. 二体运动模型下,r可表达为:

其中a、e分别为开普勒根数中的轨道半长径和偏心率, 而R可表达为:

其中i、ω分别为开普勒根数中的轨道倾角和近地点幅角,Rp为地球极半径,δ为地球扁率.

之后第二步是引入一阶长期项和一阶短周期项的影响, 对第一步处理获取的初值进行修正,得到精确的交点时刻. 这一步骤的收敛门限为|r′k - R′k| < ε, 其中k′表示第k′次迭代. 这一步迭代收敛后可得到精确的交点时刻T0, 通过交点时刻可进一步求得目标在地固坐标系的位置矢量以及轨道与地球表面精确交点的地理经纬度L和ψ.

3 有DEM支持的精确交点改进算法

原方法得出轨道与参考椭球体交点信息后, 为了进一步求得DEM支持下更精确的交点, 本文提出在原方法计算结果的基础上进行新一轮的迭代计算的新方法.

在新一轮的迭代计算中, 收敛的条件设置为|HD-HC| < ε2, 其中HC为计算求得的t时刻目标的高程,HD为通过DEM查询t时刻目标位置的经纬度得出的高程,ε2>0是给定的门限,与原方法的门限是不同的值. 本轮迭代是以高程差小于特定门限作为收敛标准, 因此该新一轮迭代过程可称为“高程迭代”部分. 具体迭代方法如下:

（1）使用原方法计算得出的交点地理经纬度L和ψ查询DEM, 得出高程HD. 再通过地固坐标系至站心地平坐标系的旋转平移转换, 可求得目标t时刻在以目标自身为原点的地平坐标系下垂直方向的速度vhz, 求得时间修正量∆t为:

（2）令T=t+∆t, 加入一阶长期项和一阶短周期项的影响, 重新外推计算得到t时刻目标的瞬时根数σ, 并由该根数计算t时刻的目标地心距r和目标在轨道坐标系中的位置矢量→r和速度矢量˙→r.

（3）通过轨道坐标系至地固坐标系的坐标旋转变换可得到t时刻目标在地固坐标系中的位置矢量, 由按以下文献[8]计算目标轨道与地球表面精确交点的地理经纬度L、ψ和高程HC:

其中Re是地球赤道半径,x、y、z分别为目标在地固坐标系位置矢量的三个分量, 此外:

（4）使用L、ψ查询DEM得出高程HD, 并通过坐标转换求得目标t时刻在以自身为原点的地平坐标系下垂直方向的速度vhz. 由下式求t时刻的修正量:

（5）令T=t+ ∆t回到本迭代方法的第二步继续计算t和∆t, 回到本步骤时, 如果满足迭代条件|HD-HC| < ε2, 则终止迭代计算过程, 否则依然回到第二步继续计算.

迭代收敛以后, 得到的计算结果就是目标位于弹道和地表的交点时更为精确的时刻t和发、落点经纬度L和ψ, 以及根据该经纬度查询DEM得到的高程值HD.

正如本文开头所述, DEM数据库中储存的高程点是离散的, 这就意味着目标轨道与地表交点区域的高程越高、坡度越大、DEM自身分辨率越高时, 可能会导致连续两次查询得到的高程数据HD的差异较大, 从而使得迭代难以收敛. 为了应对这种不收敛的情况, 首先可以增大收敛门限ε2的值; 其次可以使用优选策略: 设定最大迭代次数kmax, 当迭代次数达到kmax次时停止迭代, 选择历次迭代中|HD- HC|的值最小的那一次的迭代计算求得的L、ψ以及相应查询DEM获得的高程HD作为最优近似值, 视为最终计算结果.

4 数值实验和分析

由于缺乏实测弹道数据, 我们进行了仿真测试和分析来评估该方法的计算效能. 测试中使用的DEM数据来源于中科院网信中心地理数据云平台的SRTMDEM （Shuttle Radar Topography Mission DEM, 航天飞机雷达地形测量任务DEM数据） 90 m分辨率高程数据1http://www.gscloud.cn/., 该数据是在WGS84（World Geodetic System 84）地固系参考椭球体上的投影. 首先利用已有的成熟弹道设计软件设计得到了5组弹道, 再用试探法通过高精度数值外推得到了这5组弹道与地球表面的精确交点作为发、落点的真实值, 其轨道根数、射程及交点的高程列于表1. 本文中的射程是指惯性空间中, 导弹的轨道在地球外部那一部分的弧长. 使用的根数格式是卫星定轨中经常采用的第一类无奇点根数:除a、i和Ω外, 另外的三个根数为ξ=ecosω、η=-esinω、λ=M+ω, 其中M为轨道平近点角.

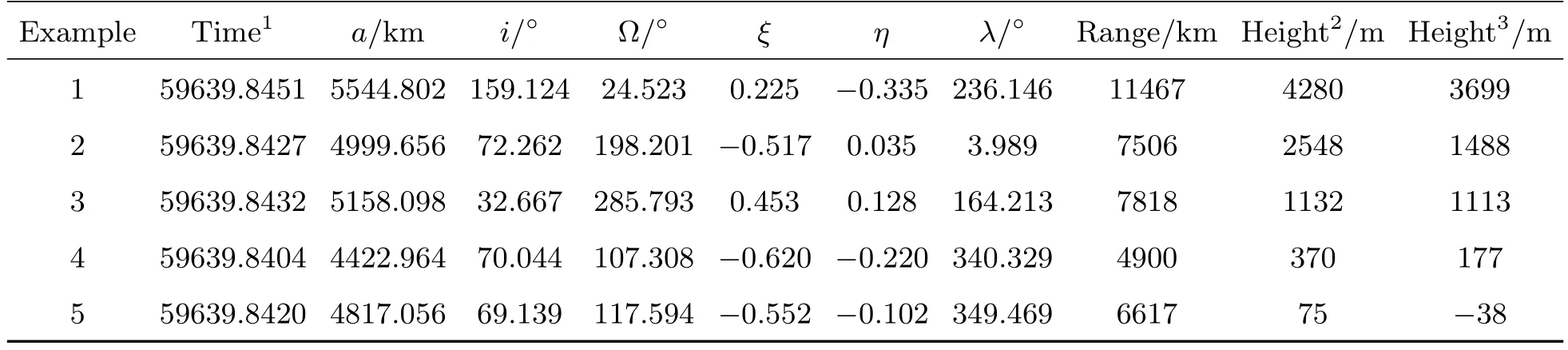
表1 仿真实验中使用的轨道根数、射程及发、落点高程数据Table 1 Orbital elements, range and elevation of launching and landing points used in simulation experiments

在实际应用中, 目标身份鉴别及预警信息生成是雷达在跟踪目标时进行实时处理的一部分, 因此模拟雷达实时处理过程, 从中考察该方法的计算效率和计算精度的变化情况是最好的选择. 我们设计实验对表1的这5组射程和高程各异的根数均进行了仿真计算. 参考文献[6]的方法, 首先根据弹道根数及发、落点选择合适的观测站址, 其次生成使用该观测站来跟踪目标的仿真观测数据, 然后在这些仿真观测数据中加入角度0.1◦、距离50 m的随机误差. 之后使用实验室已有的程序将前30 s的数据进行滤波初始化, 最后使用卡尔曼滤波程序对30 s后的每秒一点的仿真数据进行滤波来更新目标的根数.

每次滤波更新根数后, 我们分别采用原方法和本文提出的新方法产生目标两个交点的位置和时刻, 观察两种方法计算出的两个交点时刻和位置的计算误差变化. 其中原方法的收敛精度设为0.01 m,新方法的高程迭代收敛精度ε2设为1 m, 最大高程迭代次数kmax设为5次, 交点时刻位置误差的计算方法为:

其中tc和ts分别是时刻的计算值和真实值,→Rc和→Rs是地固坐标系下的位置矢量的计算值和真实值.

至于计算效率方面的变化, 新方法的计算量变化主要来源于高程迭代所增加的迭代计算, 因此在新方法计算效率的评价方面, 主要观察增加的高程迭代次数的多少. 假定滤波过程中有l次预警信息生成时进行了m（m= 1,2,···）次高程迭代,m的值可以用来评价新方法相比于原方法在计算效率上的变化. 事实上, DEM的读取速度也是影响计算效率的一个重要因素, 但其涉及的是数据库读取的相关技术, 已超出本文的讨论范围, 因此仅假定读取DEM的速度与读取内存变量速度一致, 不做进一步展开.

表2列出了各算例在生成预警信息时增加的高程迭代次数的情况, 由表2可以看出, 实验的5个算例的发、落点各自都进行了270次预警信息生成计算. 其中大部分情况下高程迭代2次即可收敛, 仅算例1和算例2的发点推算时, 超过2次高程迭代的预警信息生成次数较多, 甚至未收敛的生成次数分别为72次与99次, 这是由于这两个发点处于高程高、坡度大的山地中. 算例1的落点位于玻利维亚的乌尤尼盐沼, 此处高程变化很小, 因此虽然该点高程达3799 m, 却仍然能保证大体上迭代2次即收敛. 至于发、落点高程都很低的算例5, 全程高程迭代基本1次收敛.

表2 新方法生成预警信息时增加的高程迭代次数的情况Table 2 Increase of elevation iterations when the new method generates warning information

图1、3、5、7、9展示了5个算例的弹道目标发、落点位置误差随雷达跟踪时间的变化情况,图2、4、6、8、10展示了5个算例弹道目标发、落点时刻误差随雷达跟踪时间的变化情况. 由图1至图10可以看出, 在滤波初始阶段, 由于定轨误差较大, 因此新方法和原方法计算的时刻和位置误差均很大, 两种方法之间并无明显差异. 交点时刻和位置误差最大是算例1, 分别达上百秒和五百公里量级, 误差最小的算例5也分别达到了十几秒和百公里量级; 滤波过程进行了3.5–4 min后, 交点的时刻和位置误差均保持稳定, 此时可以看到, 对于前四个算例以及第五个算例的发点, 新方法计算得出的交点时刻和交点位置精度都好于原方法. 交点位置的高程值越大, 新方法带来的精度提升就越明显. 对于算例1的弹道交点时刻误差, 新方法的精度为0.5 s左右, 交点位置误差为3.8 km左右, 而原方法给出的两种误差分别为2 s左右和10 km左右.对于算例2–4, 新方法的交点位置和交点时刻误差分别为百米量级和0.01 s左右, 均优于原方法公里量级和0.02 s左右的误差. 对于发、落点位置接近参考椭球的算例5, 两种方法推算的交点位置和交点时刻差距很小, 对于高程75 m的发点, 新方法精度仅略微优于原方法, 而对于高程仅-38 m的落点,图9和图10显示两种方法的计算结果曲线重合在一起, 意味着两种方法的推算精度几乎一致.

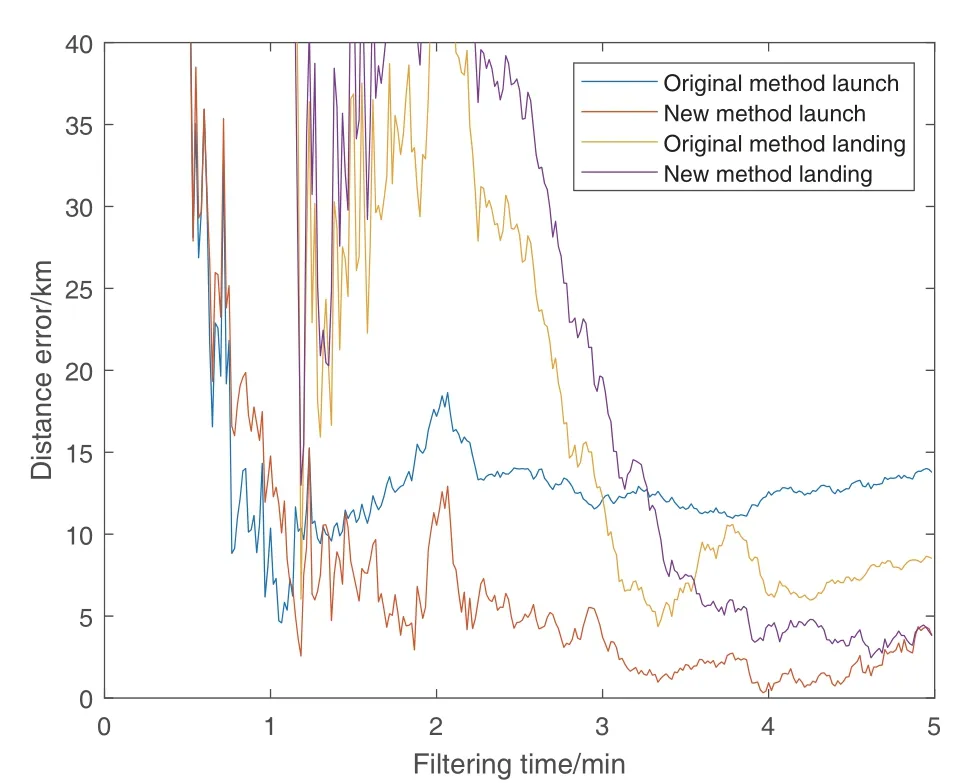
图1 两种方法对算例1的发、落点位置计算误差随跟踪时间的变化情况Fig.1 The variation of the calculation error with the tracking time for the launch and landing distance of example 1 by the two methods

图2 两种方法对算例1的发、落点时刻计算误差随跟踪时间的变化情况Fig.2 The variation of the calculation error with the tracking time for the launch and landing time of example 1 by the two methods

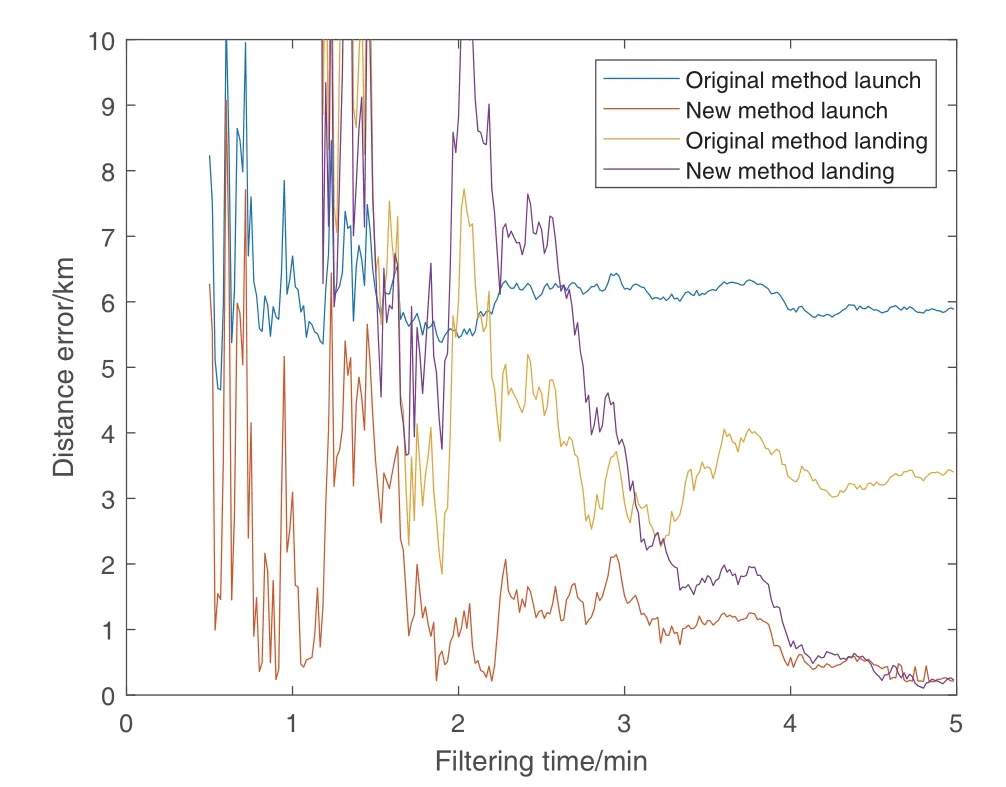
图3 两种方法对算例2的发、落点位置计算误差随跟踪时间的变化情况Fig.3 The variation of the calculation error with the tracking time for the launch and landing distance of example 2 by the two methods

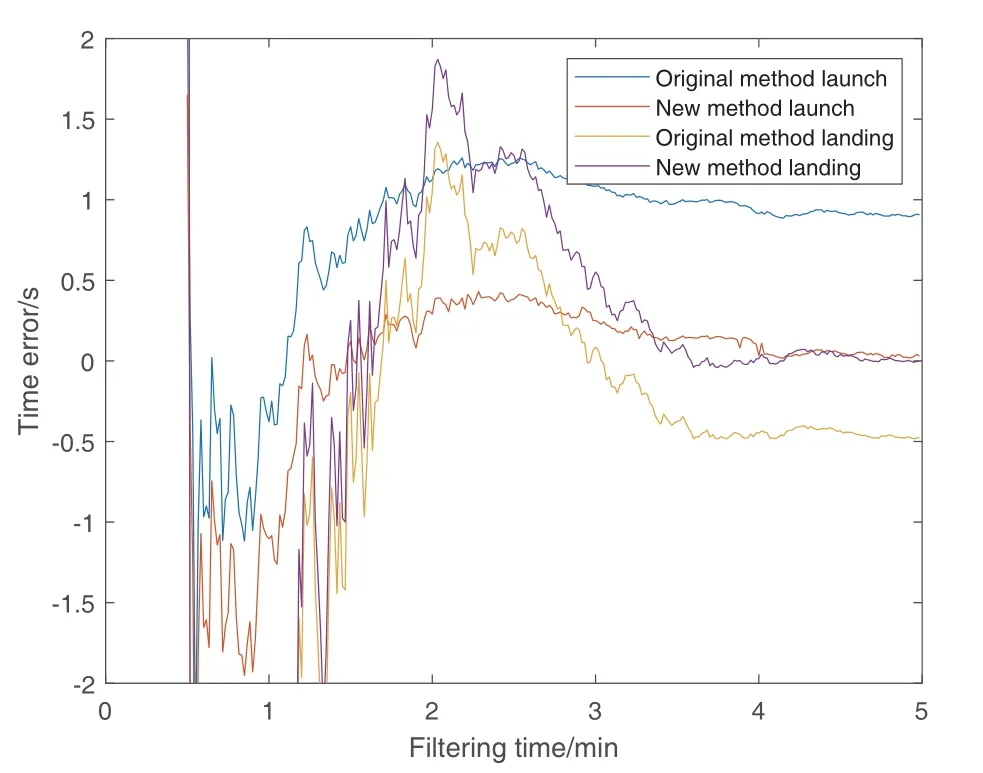
图4 两种方法对算例2的发、落点时刻计算误差随跟踪时间的变化情况Fig.4 The variation of the calculation error with the tracking time for the launch and landing time of example 2 by the two methods

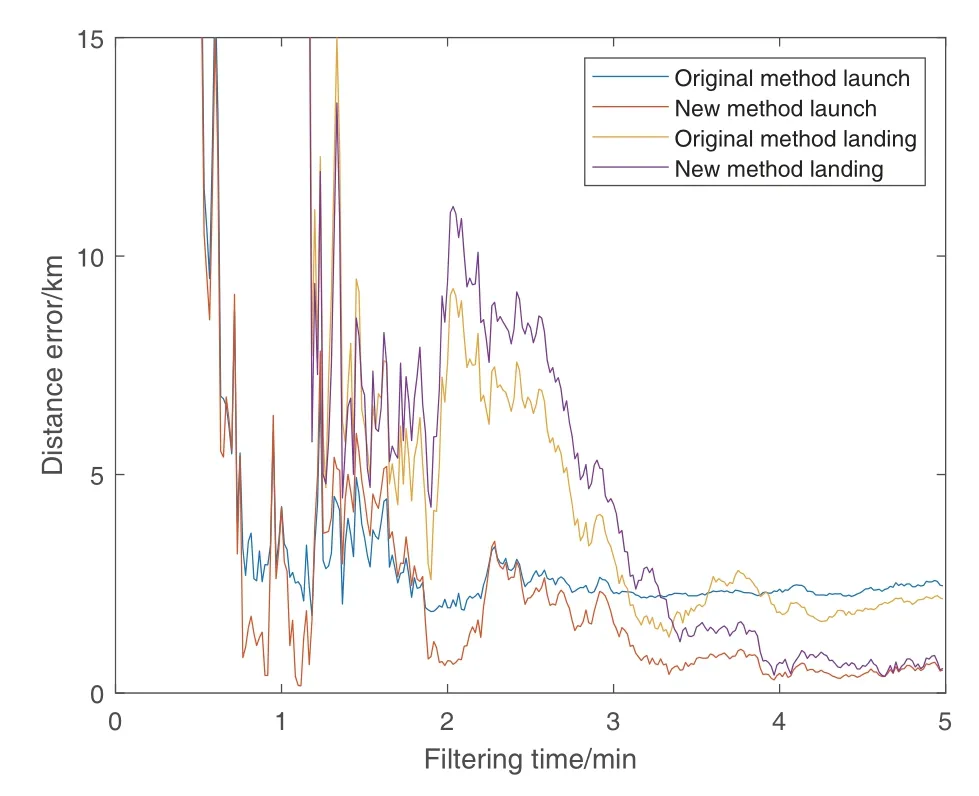
图5 两种方法对算例3的发、落点位置计算误差随跟踪时间的变化情况Fig.5 The variation of the calculation error with the tracking time for the launch and landing distance of example 3 by the two methods

图6 两种方法对算例3的发、落点时刻计算误差随跟踪时间的变化情况Fig.6 The variation of the calculation error with the tracking time for the launch and landing time of example 3 by the two methods

图7 两种方法对算例4的发、落点位置计算误差随跟踪时间的变化情况Fig.7 The variation of the calculation error with the tracking time for the launch and landing distance of example 4 by the two methods

图9 两种方法对算例5的发、落点位置计算误差随跟踪时间的变化情况Fig.9 The variation of the calculation error with the tracking time for the launch and landing distance of example 5 by the two methods

以上计算结果表明, 交点位置高程值越大, 使用新方法相较于原方法提升的交点位置和交点时刻的计算精度就越多. 对于交点高程很小的弹道,两种方法的推算结果差异并不明显. 在本实验中的大部分情况下, 每次生成预警信息时也仅增加1–2次高程迭代的计算量. 在交点高程高、坡度大时,迭代次数会增加, 未收敛的情况会增多, 但是交点位置和时刻的精度依然有大幅提升. 可见新方法加入高程迭代后, 可在增加少量迭代次数的情况下,极大程度地消除高程带来的影响.相比于其他算例,算例1采用新方法的计算精度也偏低. 这是因为其主要误差来源是较长射程导致的更久的外推时间,进而使得测轨误差有更长时间的放大. 而这一部分的计算误差显然是无法通过高程迭代消除的.

5 结论和讨论

本文基于文献[6]的研究提出了一种有高程信息库DEM支持的预警信息生成方法, 仿真实验结果表明, 该方法具有下列特点:

（1）该方法相较于原方法仅增加了少量高程迭代计算, 且对不能收敛的情况有截断和优选措施,因此能保持较高的计算速度、稳健和稳定度, 能够快速提供弹道导弹预警信息, 以供导弹防御决策;

（2）在雷达跟踪弹道导弹的实时处理过程中,该方法计算的预警信息相比原方法能够提升交点位置和交点时刻的预报精度.交点位置的高程值越大,精度提升越明显. 通常在滤波进行了3.5–4 min后,能够提供比较准确的发、落点信息, 发、落点位置和时刻的提升幅度可分别达到6 km和1.5 s. 对于发、落点高程值越小的弹道目标, 其发、落点的计算精度的提升效果会降低.

此外, 本文设计的仿真实验显示, 在设备观测的前2–3 min, 原方法和新方法计算的精度都不高,甚至出现了新方法计算的预警信息精度低于原方法的情况. 因此在实际应用中, 可以考虑在滤波达到稳态之前仅使用原方法进行目标身份鉴别和生成预警信息, 待滤波达到稳态后再加入高程迭代计算, 这样就可以在不影响总体预警信息精度的前提下, 减少多次高程迭代计算以及DEM数据库读取操作, 从而在观测设备跟踪过程中进一步提高计算速度和效率.

需要说明的是, 在实际情况下目标在主动段的受力过程难以获知, 因此即使使用本文的方法计算的发点信息仍然会有较大误差. 落点计算则不同,设计弹道一般要求在不考虑大气动力影响的情况下准确到达落点. 在此阶段的控制调整主要任务是使目标能准确击中指定地点, 因此, 采用本文的方法来提升落点位置时刻的精度会有较大的应用价值.